不定积分的求解方法及应用

郭 晓，张晨晨

(南阳职业学院，河南 南阳 474500)

不定积分的求解方法是积分问题的基础，本研究结合例题对不定积分的各种求解方法进行分类和总结归纳，旨在找到最简单、最快捷、最有效的解题方法。需要掌握的预备知识：设F(X)与f(x)在区间I上有定义，若∀x∈I，有F′(x)=f(x)或dF(x)=f(x)dx，则称F(x)为f(x)在区间I上的一个原函数。

1 不定积分

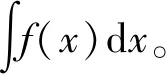
2 不定积分的性质

3 基本积分公式

在运用直接积分法时会用到基本积分公式，下面先给出基本积分公式：

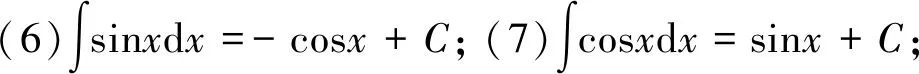
4 直接积分法

在求积分问题时，简单的不定积分可以直接利用法则和公式，稍微复杂的，可以先对被积函数做恒等变形，变形成可以利用积分的法则和公式的形式，然后按基本积分公式求出结果。

=3arctanx-2arcsinx+C.

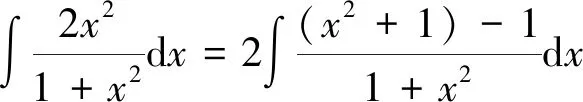
5 换元积分法

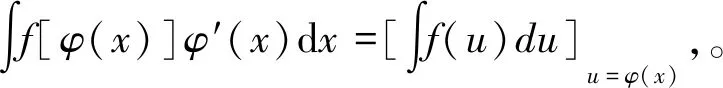
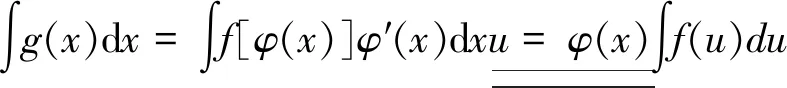
=F(u)+c(积分)=F[φ(x)]+c(回代).

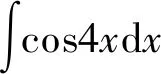
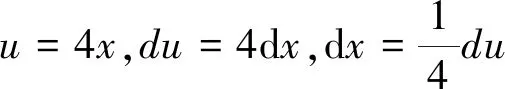
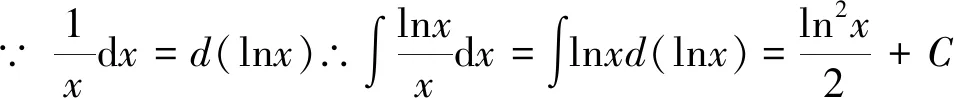
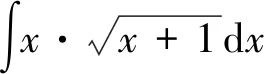
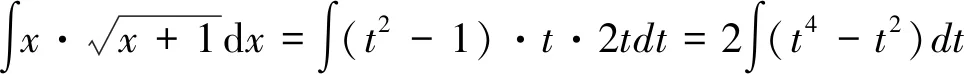
第一类换元积分法的关键是如何选取φ(x)， 并将φ′(x)dx凑成微分dφ(x)的形式，因此，第一类换元积分法又称为凑微分法。

在换元积分法中，有一些特殊形式的换元，如：根式代换、三角代换、倒代换。

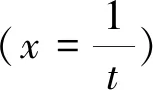
有些不定积分的结果会经常用到，可作为基本公式：

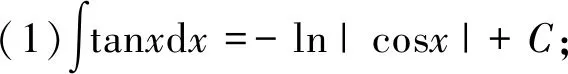
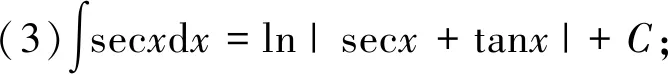
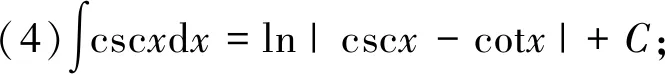
6 分部积分法

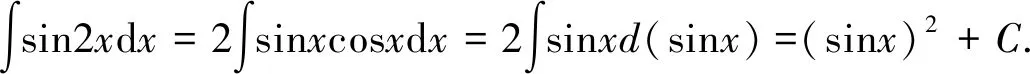
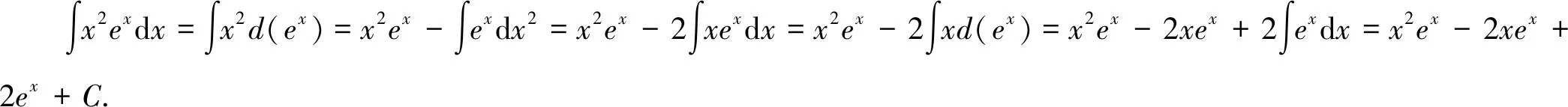
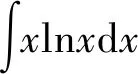
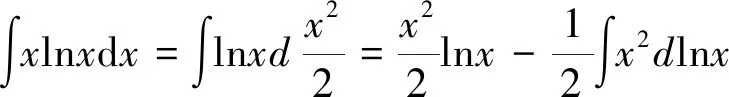
在分部积分法中，u,v的选择方法可总结如下：学生可简化记忆，按照反、对、幂、三、指这个顺序，优先选择前面的函数为u，另外一个函数与dx结合凑微分，然后运用分部积分公式进行计算。

7 结语

不定积分具有很强的计算灵活性，学生需要做大量的练习，积累更多的经验，这样解起题来才能得心应手。