不确定需求下应急食品调度鲁棒优化模型

文/石崇玉 方瑜

1.前言

2020年，全球突发性公共卫生事件爆发。其中武汉应急食品的调度存在各种各样的不确定性因素。公共卫生事件出现期间，武汉进入紧急战役状态，超市库存不断减少，当地果蔬供应中断，因为这些原因导致我们无法获得食品需求量等数据，所以受影响区域的食品需求量是不能准确确定的。考虑到各种不确定性因素对应急食品调度优化模型的影响，我们来讨论在不确定需求下疫情应急食品调度鲁棒优化模型。通过构建模型，探究公共卫生事件中应急食品物资调度现状，通过建立疫情中食品应急调度模型，为实现满足受影响地区人民对应急食物的需求。本文将考虑不确定需求下构建鲁棒优化模型，以求找到最优调度路线来满足疫情区域内的食品需求。

2.理论分析

2.1 不确定性理论。任何事物在其发展、演化的过程中会受到很多不同方面因素的影响，这将使其一直处在一种模糊、混乱、不稳定的状态中，这一系列过程即被看作是事物的不确定性。不确定性可以理解为不肯定性、变化性、随机性、偶然性、不准确性。不能准确地反映事物本质特征的信息统称为不确定性信息。现实生活中经常会用到这类不确定性信息。随着人类文明的不断进步，科学技术正在迅猛发展，人类对不确定性信息的理解会更加深入，如果忽视该类信息的存在或无法对该类信息进行科学有效处理，将无法客观、公正对事物本源进行正确的认识，也不能科学地研究复杂的系统问题。我国的食品应急物资需求存在着不确定性。特别是在疫情期间，随着公共卫生事件形势加剧，感染人群增多会给食品的物资的需求带来不确定性，这些不确定性会严重影响食品物资供应以及救援工作。因此需要运用不确定性理论分析出在各种不确定情况下，找到一种符合情况的算法或者模型。正确预测出对食品的需求

2.2 鲁棒优化理论。鲁棒优化方法是研宄不确定优化问题的一种重要的方法，是解决由于内部参数或外部环境所产生不确定性的一种新的优化方法。鲁棒优化的目的是求得这样一个解，对于可能出现的所有情况，约束条件均满足，并且使得最坏情况下的目标函数的函数值最优。鲁棒优化的关键是建立相应的鲁棒对等模型。然后利用相关的优化理论将其转化为可求解的“近似”鲁棒对等问题并给出鲁棒最优解。因此本文将不确定需求下疫情应急食品调度模型的鲁棒优化定义为：在不确定需求的条件下得到的优化解，对于应急救援任务出现的任何可能情况都是可行的对结果造成的波动都在可接受范围之内，不会产生过大的损失。

3.不确定需求下疫情应急食品调度鲁棒优化模型

3.1 模型的基本假设。食品调度分为两部分，第一部分是将应急食品从周边供应点送至食品中转站，第二部分为从中转站直达疫情灾区。对于该问题，我们考虑时间最小化，成本最低化为目标函数，选取最佳的配送路线。不确定需求的应急食品调度模型将无法得到准确的食品需求量，因此我们提出以下假设：（1）假设各个供应点和中转站拥有足够数量的车辆以及车辆运载容量。（2）不考虑车辆的装卸搬运占用的时间，也不包括运输完后的分发时间。（3）不考虑建设成本以及车辆成本（4）供应点的供应量能满足疫情地区的需求量。（5）因疫情特殊性无法获得准确的食品需求数据，在此我们将用一个区间来表示不定的需求量。

3.2 符号说明。根据以上假设，以下为本模型将用到的相应指标、参数和决策变量

（1）集合：供应点集合I（i=1，2，3…，I）；中转站集合（j=1，2，3…，J）；疫情灾区集合 K（k=1，2，3…，K）

（2）决策变量：xij：表示从供应点i到中转站j的调度应急食品数量；yjk：表示从中转站j节点到疫情灾区的调度应急食品数量；ajk∈{0，1}：供应点i到中转站j路径是否使用，1为使用，否则不使用；βjk∈{0，1}：在中转站j到疫情灾区k路径是否使用，1为使用，否则不使用；zj∈{0，1}：中转站 j是否建立，1为使用，否则不使用

（3）参数变量：cij：在供应点到中转站间，车辆的单位运输成本；tij：在供应点到中转站间，车辆的运输时间；mk：疫情地区对应急食品的需求量；wk：疫情地区对应急食品的缺货量；b：未满足疫情地区需求量的缺货惩罚系数；fi：食品供应点的食品仓储数量；ej：食品中转站的最大中转存储量；M：为无穷大数值。

本文考虑到疫情地需求不确定的情况，在以上基础上，设立以下参数：：模型中为区间数，是每个疫情灾区对于应急食品的需求量区间为疫情灾害地对食品需求量的预测值是实际情况中食品需求量与预测值的最大差值。：为区间数的上限；mk：为区间数的下限，表示需求点对食品物资的最低需求量；食品需求量：设疫情地对食品需求数量的最小值等于该地对食品需求量的预测值，即设疫情地对食品的最大需求量等于食品需求量的预测值与最大扰动值之和，即

3.2 不确定需求下疫情应急食品调度模型。根据以上假设，所建模型如下所示：

（3-1）表示供应点i到食品中转站j的运输时间和食品中转站j到疫情地区k的运输时间之和的最小值；（3-2）表示供应点i至食品中转站j的运输费用与食品中转站j到疫情地区地k的运输费用，以及缺货成本之和的最小值；（3-3）表示向疫情地区运输食品的数量与疫情地区食品的缺少量之和处于疫情受灾地的食品实际需求量与预测需求量区间之内；（3-4）表示食品供应点i向中转站j的食品供应量小于等于食品供应点i的最大存储量；（3-5）表示食品供应点i向中转站j的食品供应量小于等于中转站j的最大存储量；（3-6）供应点i运抵中转站j运输食品的数量等于中转站j到疫情地区运输食品的数量；（3-7）供应点i到中转站j的食品运输量是大于等于0是基于该路径投入使用的情况下；（3-8）中转站j转运储存的食物量是基于该中转站是否投入使用的情况下；（3-9）中转站j到疫情地区k的食品运输量是大于等于0是基于该路径投入使用的情况下；（3-10）表示取1时路径、中转站投入使用，否则不投入使用；（3-11）表示i到j，j到k的食品运输量，疫情地区的物资需求区间大于等于0。

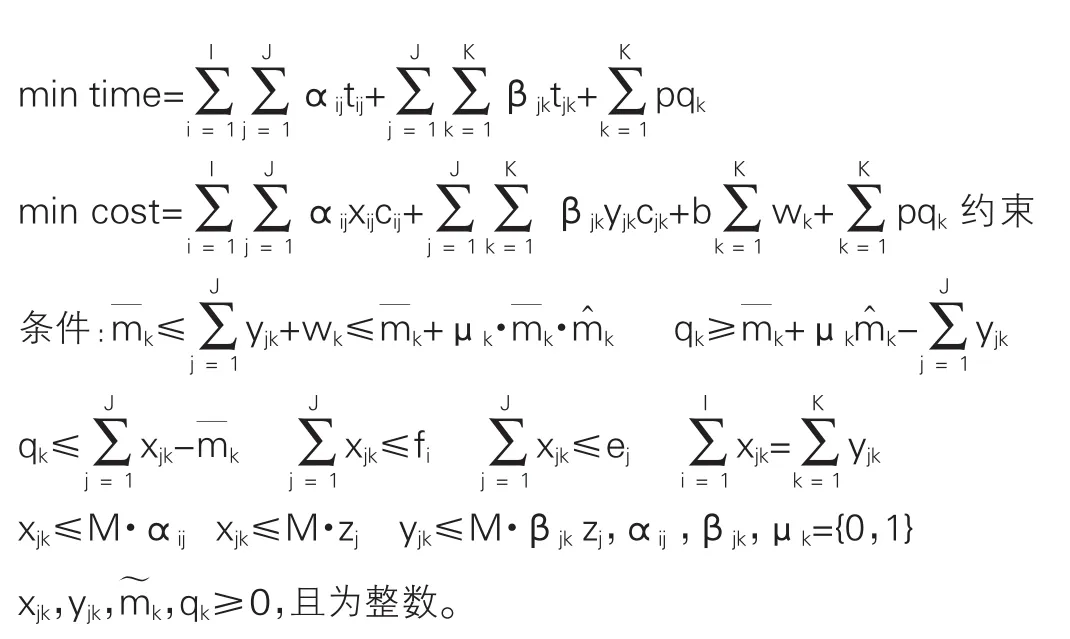
3.4 模型算法。本章建立的是多目标鲁棒优化模型，可以采用线性加权和法，令ri为第i个目标函数的权重系数，且∑ri=1。根据目标函数，将时间目标权重系数定为r1，成本目标权重系数定为r2，将其转换为新的单目标函数并使用软件lingo11求解。

4.案例分析

4.1 数据处理

（1）集合

供应点集合I（i=1，2，3…，I）。武汉在此时其，根据国家和省市应对公共卫生事件期间粮油供应要求，周边供应点：

1）武汉大花岭库粮油；2）武汉东西湖区益海嘉里；3）武汉市洪山库粮油；4）武汉市白沙洲。

受影响地区集合 K（k=1，2，3…K，），由于公共卫生事件在武汉市区比较聚集，而物资配送区域也是整个武汉市在内，所以可以直接选用武汉市的6个区域：江岸区、江汉区、硚口区、汉阳区、武昌区、青山区。中转站集合 J（j=1，2，3…，J），根据武汉市六个区域的面积以及相关地理位置，考虑到模型中有四个供应点以及六个需求点，本文将设置三个区域作为中转站连通供应点和需求点，通过比较各区域与两点的距离以及交通便利程度，我们选取如下图的江汉区、汉阳区、洪山区三个区域作为中转站。

图1 武汉市区图

（2）参数变量：cij：在供应点到中转站间，车辆的单位运输成本。大型货车的运输费用一般为0.5元每吨每公里左右，本文考虑到在此非常时段，运输价格会有所增加，因此我们假设这一时段大型货车的运输费用为1元每吨每公里，再根据百度地图提供各点之间的路径距离，得出以下单位运输成本。运输时间：本文运输时间由百度地图得到各点之间的距离，按货车在城区公路行驶的平均速度30千米每小时来计算得出，不计配送前及配送后装卸搬运的时间。

表1 供应点i到中转站j车辆的单位运输成本（单位：元/吨）

表2 中转站i到疫情地区k单位运输成本（单位：元/吨）

表3 供应点i到中转站j车辆运输时间（单位：小时）

表4 中转站j到疫情灾区k车辆运输时间（单位：小时）

因公共卫生事件原因，百姓主要以蔬菜作为主食，因此本文在应急食品需求量上以武汉居民平时的蔬菜交易量作为依据推断。根据武汉三大商超2020年2月1日蔬菜销量1058t以及2020年初武汉市总人口906.3万人与各区域人口来估算居民每日蔬菜需求量。（注：数据来自今日头条和武汉统计年鉴）

表5 疫情地区k对应急食品的需求量（单位：t）

表6 食品工业的仓储数量（单位：t）

4.2 模型求解

在此次配送中，因疫情特殊原因，时间是首要的，而成本为其次，因此本文设时间权重r1=0.8，成本权重r2=0.8，需求未被满足时成本惩罚系数b=10，鲁棒扰动系数为10%。通过lingo11计算得到以下表格

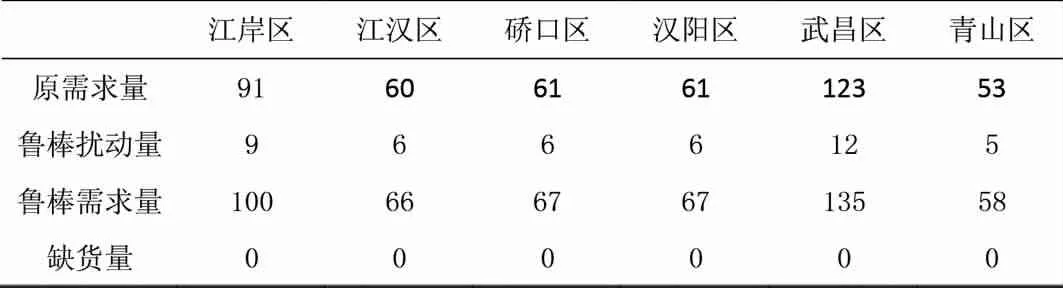
表7 疫情灾区食品需求表（单位：t）

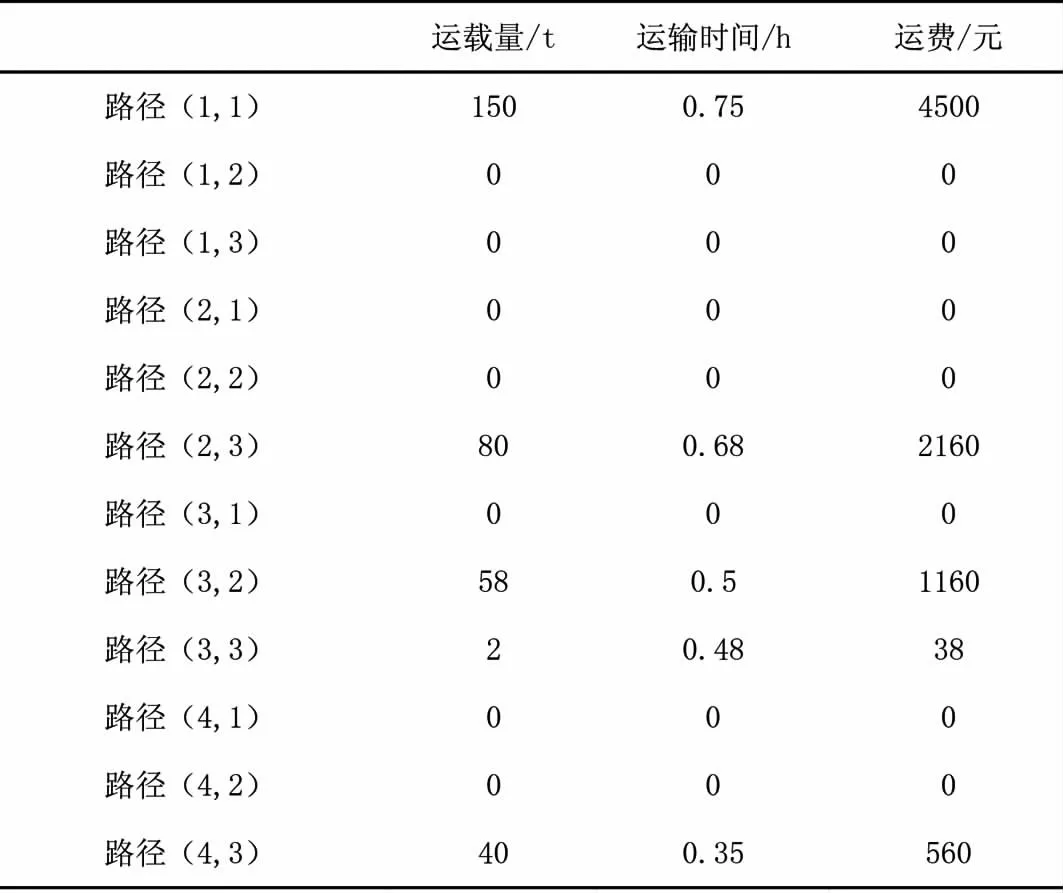
表8 供应点i到中转站j调度表

配送方案为：由大花岭库粮油向江汉区中转站配送150t货物，东西湖益海嘉里物资中心向武昌区中转站配送80t货物；洪山库粮油向汉阳区配送58t货物，向武昌区中转站配送2t；白沙洲物资中心向武昌区中转站配送40t货物。总结供应点到中转站应急食品物资配送耗时0.75小时，合计共耗时2.76小时，运输成本8418元。

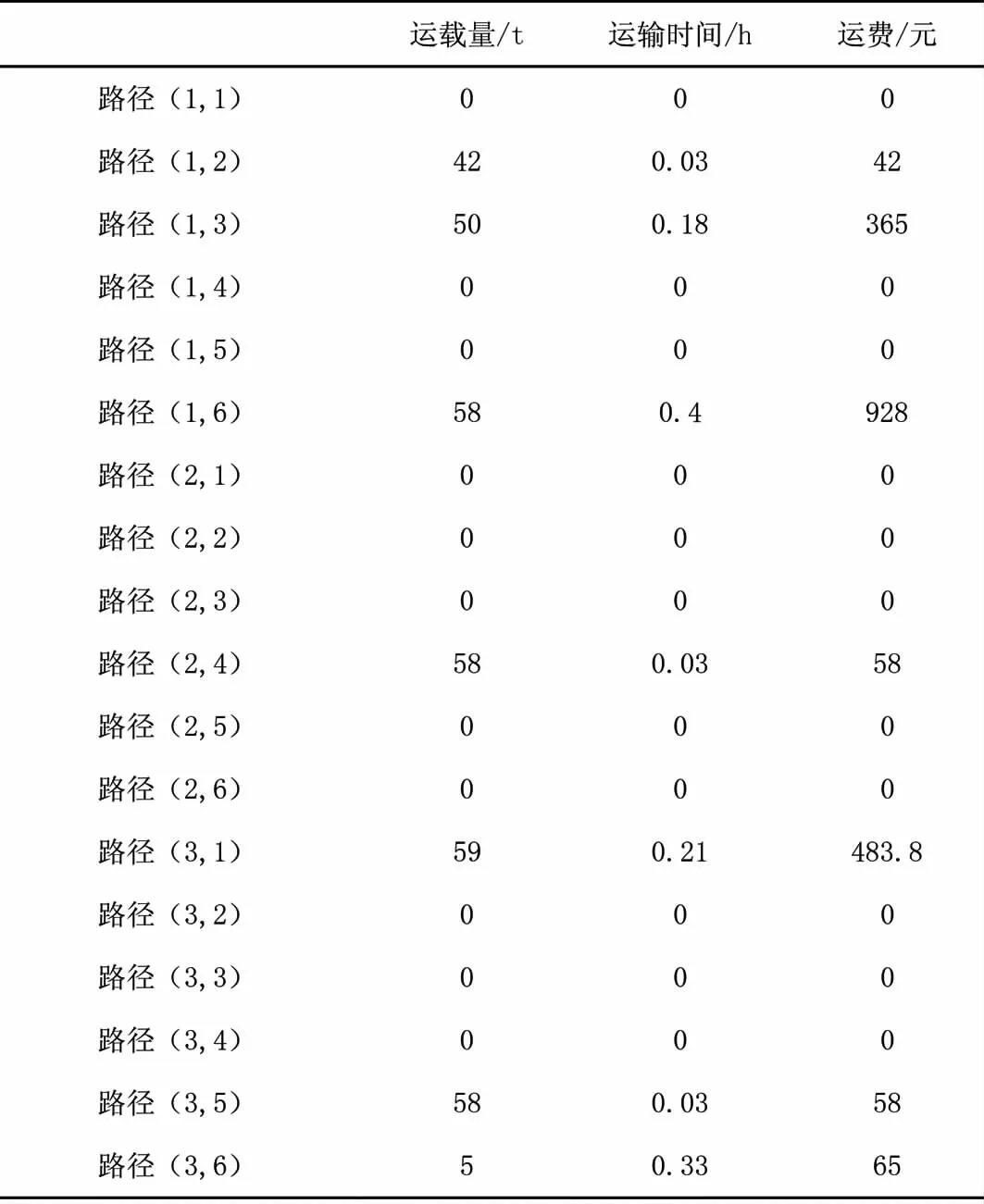
表9 中转站j到疫情灾区k调度表

配送方案为：由江汉区中转站向江汉区疫情地区配送42t货物，向硚口区疫情地区配送50t货物，向青山区疫情地区配送58t；汉阳区中转站向汉阳区疫情地区配送58t；由武昌区中转站向江岸区疫情地区配送59t货物，向武昌区疫情地区配送58t物资，向青山区疫情地区配送5t物资。总结中转站到疫情地区应急食品物资配送耗时0.4小时，合计共耗时1.21小时，运输成本1999.8元。配送方案至此整个过程耗时1.96小时，运输成本10417.8元。

5.总结。

本文章通过对公共卫生事件下应急食品调度现状分析，查阅关于鲁棒优化问题、需求不确定供应链、多目标选址、应急救援供应链等文献，灵活运用不确定性理论及鲁棒优化理论，构建成不确定需求下多目标鲁棒优化模型。其中因需求的不确定性，将需求量定义为一个区间值，最后利用Lingo软件进行求解。在最坏的情况下使成本及时间达到最优，即达到将应急救援物资快速高效及低成本地运达受影响地区，满足这些地区人民食品需求的目的，解决这些地区食品无法达到自给自足的问题。因此本文建立的不确定需求下应急食品鲁棒优化模型在某些方面现实实际情况中可以给予一定帮助，具有一定现实意义。