循环荷载作用下软土地基强度弱化模型研究

李芬，杨宇，彭晓宇，王鹏达，胡丹

(1.武汉理工大学 船海与能源动力工程学院，湖北 武汉 430063；2.湖北省交通投资集团 鄂西高速公路建设管理有限公司，湖北 武汉 430050）

自从国家“十三五”规划提出科技兴海战略以来，我国港口建设高速发展。随着适宜建港的天然海岸已被开发殆尽，新港址往往处于深水、复杂波流荷载以及软弱地基等不利环境条件下[1]。在我国近海地区覆盖着力学性质较差的软黏土，具有含水量高、压缩性大、承载力低等特点，且在风、浪等循环荷载作用下会发生强度弱化[2]，可能导致上部结构物出现过大的滑移、沉降变形，进而严重威胁结构物的安全使用[3]。WANG等[4]指出软黏土的强度弱化往往是由孔压累积引起的。目前关于循环荷载作用下软黏土强度弱化的研究，主要从建立土体本构模型和基于动三轴试验拟合孔压模型2方面展开。刘恩龙等[5]假定土体在细观尺度上为由大量胶结元和摩擦元组成的二元结构体，基于岩土损伤力学建立了二元介质弹塑性模型，并引入反映破损过程的破损参数和应力比来描述结构性土体的变形特性；侯丰等[6]基于有限元方法实现了刘恩龙等[5]提出的二元介质弹塑性模型，对天然边坡开展数值计算，指出模型参数的敏感性还有待进一步研究；马文国[7]基于修正剑桥模型建立了边界面弹塑性模型，该模型能反映形状参数、饱和黏土的结构性、各向异性的影响，可用于描述原状饱和黄土在静力、循环荷载作用下的力学特性和机理；CHENG等[8]则基于修正剑桥模型，引入塑性模量插值函数，提出了一种考虑循环弱化效应的弹塑性边界面简化模型。上述学者针对饱和黏土提出的本构模型参数较多，计算较为复杂，难以直接应用于实际工程中。近年来，还有大量学者基于动三轴试验方法对软黏土循环动力特性开展了大量研究。周建[9]通过对饱和软黏土开展循环动三轴试验，探究了循环应力比、循环次数、荷载频率以及超固结比等因素对孔压发展规律的影响；王军等[10]对杭州饱和软黏土开展循环动三轴试验，拟合了土的软化指数与循环次数的对数关系及残余孔压发展规律；栾茂田等[11]研究表明，基于动三轴试验的拟合模型计算得到的土体强度偏大，有必要进行修正；YAN等[12]对双曲线孔压模型进行了修正。总的来说，基于动三轴试验拟合得到的孔压模型参数较少且易于实现，因此在实际工程中得以广泛应用。本文基于动三轴试验建立孔压模型，并提出土体循环荷载作用下软黏土的不排水抗剪强度弱化模型。基于有限差分软件FLAC3D数值实现该模型，并与试验数据对比验证采用该模型描述循环荷载作用下软土地基弱化的可行性，为实际近海工程结构物的稳定性分析奠定基础。

1 软黏土强度弱化模型的建立

饱和软黏土在循环荷载作用下会产生刚度软化、强度降低的现象，从而导致土体承载力降低甚至发生破坏。周建[9]认为，循环荷载作用下，软黏土力学性质改变的原因可分为3类：1)循环荷载作用引起土体孔隙水压力上升，导致土体有效应力降低；2)循环荷载作用下土体主应力方向不断发生改变，导致土体结构重塑；3)较高的循环应力长期作用会影响土体原有结构。工程上更多是因为孔隙水压力上升导致土体有效应力降低，地基承载力不足发生结构失稳。因此，本文从孔压累积引起有效应力降低这一角度展开研究，对饱和软黏土在循环荷载作用下的弱化机理进行深入分析，结合孔压发展模型与等效超固结理论得出软黏土强度衰减时程规律。

1.1 孔压模型的拟合

软黏土循环加载下孔隙水压力累积发展的研究已开展过许多工作，周建等[9-12]针对软黏土孔压发展规律，提出了对数模型、指数模型、双曲线模型等孔压模型。其中CHEN等[13]提出的双曲线型孔压模型参数简单，物理意义明确，具有良好的适用性，

式中：孔压比u*为孔隙水压力u与初始固结压力σc的比值；N为循环次数；N50为孔隙水压力等于σc/2时对应的循环次数；a=1.051 2，b=0.948 8。

目前研究大多集中于探究孔压随土体模量和阻尼比的变化规律。李晓飞[14]研究了土体的最大剪切模量和极限剪应力在地震荷载作用以及不同固结比下随孔压增长的变化差异；刘干斌等[15]研究了不同温度下土体的孔压、阻尼比以及动弹性模量的变化规律。然而，李校兵等[16]研究发现结构物自重引起的静偏应力、动应力、应力路径、初始剪应力等对孔压发展有很大影响。因此，本文基于CHEN等[13]提出的双曲线孔压模型，提出了考虑静偏应力和动应力对孔压发展影响的双曲线孔压修正模型，如式(2)所示。

式中：A，B为与静偏应力和动应力相关的试验参数；C为孔压最大值umax与初始固结压力σc的比值。由式(2)可知，当循环周次N趋于无穷次时，孔压比u*的值等于C。尽管软黏土孔压发展规律受试验条件、土体力学性质等因素影响，但孔压发展稳定后的孔压最大值C受内、外部因素干扰较小，容易测量。因此，对于试验条件和力学性质不同的软黏土来说，该孔压发展模型都具有较强的适用性。

基于式(2)对杨攀博[17]的孔压发展曲线进行拟合，相关试验参数的拟合结果见表1。为了便于描述静偏应力σj和循环动应力σd对孔压发展规律的影响，本文引入了静偏应力比h和动应力比r2个变量，分别表示为：

由表1可知，孔压与静偏应力比、动应力比相关，这二者反映了孔压的最大值，以及孔压的发展速度。因此，可以将试验参数A，B，C表示为与静偏应力比、动应力比相关的参数。

表1 试验参数拟合Table 1 Fitted test parameters

通过线性回归分析，可以得到参数A，B，C与静偏应力比和动应力比相关的表达式，如式(4)，(5)和(6)所示。

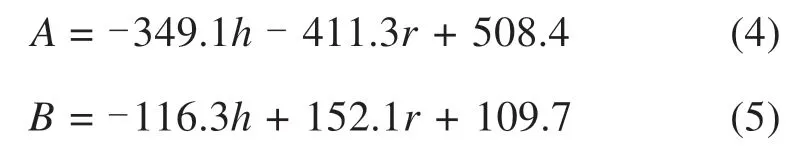
将式(4)，(5)，(6)代入式(2)，可以得到能反映静偏应力、固结应力、动应力和循环周次影响的孔压比发展模型，如式(7)所示。

由式(7)得到在不同静偏应力比和动应力比下，孔压比随循环加载次数的发展曲线，如图1(a)～图1(c)所示，h=0,0.4,0.8时孔压比拟合曲线与试验实测曲线基本保持一致，拟合效果良好。

图1 不同试验条件下孔压比与循环周次关系Fig.1 Variation of pore pressure ratio with cycle numbers under different test conditions

1.2 强度弱化模型的建立

YASUHARA[18]指出，在循环荷载作用下，土体孔压累积导致有效应力降低，进一步提出了土体循环荷载作用下不排水强度的弱化模型：

式中：(Su)cy表示循环荷载作用后土体的不排水剪切强度；(Su)为正常固结土体的不排水剪切强度；CC，CS分别表示土体的压缩系数和回弹系数；Λ0为试验常数。定义强度折减系数β为相同围压下软黏土循环荷载作用后和作用前不排水剪切强度的比值，将式(7)代入式(8)，可以得到循环荷载作用下软黏土不排水剪切强度折减系数β：

下面依据动三轴试验结果和式(9)，对m进行拟合，不同动应力比和静偏应力比组合下的β和m值如表2所示。

表2 强度折减系数β和参数m统计Table 2 Calculated cyclic degradation coefficients β and m

采用式(9)对不同组合下的m值进行反演，发现m值并不随静偏应力比和动应力比表现出规律性变化，除去几个明显偏离的点，m值一般在0.13至0.18之间。

YAN等[12]指出在工程允许的误差范围内，可选取参数m的平均值。由表2可知，式(9)拟合反演得到m的平均值为0.162，与杨攀博[17]通过试验得到的值m=0.156基本一致，验证了本文计算方法的正确性。

2 软黏土强度弱化模型二次开发

2.1 强度弱化模型的数值模拟实现

基于FLAC3D软件的内嵌程序语言FISH，用户可以定义新的变量和函数，通过二次开发满足计算分析需求。本文基于FLAC3D中的FISH语言，将软黏土强度弱化的变化过程通过土体强度指标黏聚力c和内摩擦角φ的动态变化表现出来，从而实现软黏土强度弱化。

由摩尔-库仑模型屈服准则可知：

式(10)中：τ为抗剪强度；σ是剪切面法向应力；φ是内摩擦角；c是黏聚力。

将强度弱化模型与摩尔-库仑屈服准则相结合，结合公式(9)～(10)可得：

式(11)中：τ'表示软黏土循环抗剪强度，随着荷载循环周次增加逐渐发生衰减。

本文将土体强度弱化体现在强度参数的动态变化中，随循环荷载次数N增加，土单元的内摩擦角φ'和黏聚力c'可表示为：

本文基于FISH语言采用循环函数实现土体强度参数的变化，开发流程如图2所示。详细步骤为：

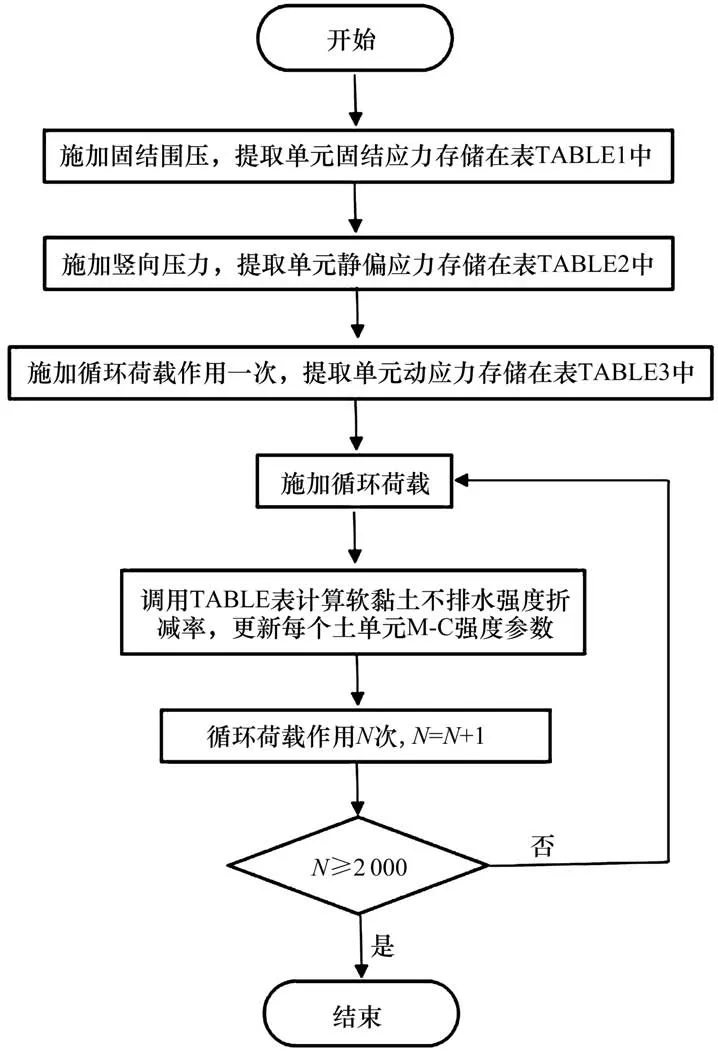
图2 软黏土强度弱化数值模拟开发流程Fig.2 Numerical simulation of soft clay cyclic degradation

1)计算土单元在固结围压作用下产生的固结应力、上部结构自重引起的静偏应力、循环荷载作用产生的动应力，分别存储在TABLE表中。

2)调用TABLE表，由式(9)计算软黏土不排水强度折减率β，更新土体单元的强度参数，作为下次循环的初始条件。

3)判断是否达到设定的循环次数，没达到则继续施加循环荷载，达到则计算结束。

该动力分析模型能够输出循环荷载作用后土体的强度折减系数和折减后的强度参数，进而反映整个循环荷载作用过程中软黏土的强度弱化过程，能够有效地模拟软黏土地基弱化效应时结构物与地基相互作用的演化规律。

2.2 强度弱化模型的验证

基于有限差分软件FLAC3D模拟验证杨攀博[17]的动三轴试验数据，实现过程如下：

1)建立边长1.0 m的三维实体单元，本文主要模拟土体的抗剪强度折减，不需要建立圆柱形模型。模型示意图如图3所示。

图3 数值模拟土样模型Fig.3 Numerical simulation of soft clay model

2)设置材料本构模型和基本参数，土体的基本参数取自杨攀博[17]的试验数据，见表3。

表3 动三轴试验模型参数Table 3 Triaxial test parameters of soft clay

3)固定试样的3个面，分别为试样底面、X方向的一个侧面和Y方向的一个侧面，然后在另外3个面施加围压。

4)在试样顶面施加竖向力获得土体的静偏应力，施加正弦形式的动应力作用一次获得土体的动应力，然后施加正弦形式的循环应力作用至试验循环次数。

5)输出强度折减率和土体抗剪强度参数随时间变化的曲线，与试验结果进行比较。

试验选用的荷载组合为：σc=35 kPa，σi=0 kPa，σd=0.4 kPa，试验结果见表4。模拟得到的强度折减系数随循环周次变化曲线与试验结果对比如图4所示，内摩擦角和黏聚力随循环周次变化曲线分别如图5和图6所示。

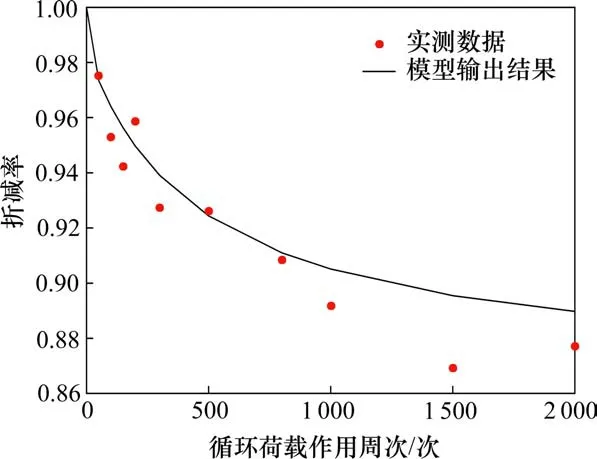
图4 强度折减系数模拟曲线与试验数据对比Fig.4 Comparison of the calculated and the measured results

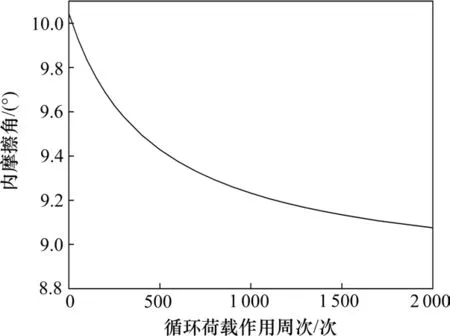
图5 数值模型输出的内摩擦角弱化曲线Fig.5 Calculated internal friction angle degradation curve

表4 不同循环周次下强度折减系数实测结果Table 4 Measured cyclic degradation coefficients

图6 数值模型输出的黏聚力弱化曲线Fig.6 Calculated cohesion degradation curve

基于上文建立的动力分析模型，对土体的抗剪强度在不同动应力和静偏应力下的弱化情况进行模拟，输出不同组合条件下软黏土不排水强度折减系数β随循环荷载次数变化的曲线，如图7所示。

图7 不同应力比下折减系数β与循环周次关系Fig.7 Relationship between cyclic degradation coefficients β and cycle numbers under different stress ratios

由图7可知，循环荷载作用初期，软黏土不排水抗剪强度衰减的速率较快；随着循环荷载作用周次的增加，强度衰减的速率逐渐变缓，当循环荷载周次达到1 500次以后，衰减趋于稳定；由静偏应力比和动应力比不同组合情况下模拟得到的抗剪强度衰减曲线可知，当土体产生的静偏应力和循环动应力越大，软黏土强度折减系数趋于稳定时的值越小，软黏土强度弱化的程度越大。

该规律综合考虑了土体初始固结应力、动应力、结构自重产生的静偏应力和加载周次的影响，不再只是反映某固定时刻土体的强度弱化状况，而是具体地体现了土体在循环荷载作用过程中每个时刻的强度弱化情况，能够反映土体的强度弱化随循环次数的发展规律。

3 结论

1)通过对动三轴试验数据进行拟合，建立了能够综合反映固结压力、静偏应力、动应力和循环次数的累积孔压发展模型。

2)将软黏土累积孔压发展模型与等效超固结理论相结合，建立了软黏土不排水强度弱化模型。该模型反映了软黏土不排水强度随着循环周次增加逐渐弱化，土体的静偏应力比和动应力比越大，土体强度弱化程度越大，且弱化速度越快。

3)基于FISH语言对有限差分软件FLAC3D进行二次开发，数值实现了考虑循环荷载作用下软黏土强度弱化效应的动力分析模型。