从问题情境到模型识别复习动量守恒定律
2022-01-20云南张文杰
云南 张文杰
一、物理模型及其物理核心素养
物理模型来源于生活,又高于生活。物理模型是物理学家从纷繁复杂的现实情境中,抓住问题研究中的主要因素,忽略次要因素而抽象出来的理想化的客体。例如:质点、刚体、弹簧振子、点电荷、斜面、轻绳等。它们是对物理研究对象的简化和描述,通过对模型的研究得到的物理规律,又对社会生产实践进行指导。
《普通高中物理课程标准(2017年版)》(以下简称课程标准)中提出了物理学科核心素养这一概念。学科素养是学科育人价值的集中体现,是学生通过学习而逐步形成的正确价值观、必备品格和关键能力。物理学科核心素养包括“物理观念”“科学思维”“科学探究”“科学态度与责任”。其中“科学思维”中的模型建构是科学思维的重要体现。高中课程标准中提出学生具有建构模型的意识和能力,是在以前的“过程与方法”基础上的深化和具体化。
二、“动量守恒定律”教材的特点和高考要求
高考根据课程标准和《中国高考评价体系》确立了“核心价值、学科素养、关键能力、必备知识”,简称“一核四层四翼”。物理学科从“四翼”出发,具体要求:基础性、综合性、应用型、创新性。物理学科考查载体为问题情境,主要分为:生活实践问题情境和学习探索问题情境。2017年后,高考将选修3-5纳入必考部分,19版人教版教材直接纳入必修第三册内容。动量守恒定律是培养物理学科核心素养的有效载体,体现了“物理观念”中的运动与相互作用观念、能量观念,在“科学思维”中的模型建构、科学推理、科学论证等方面都有很好体现。笔者最近在上动量守恒定律的课程时,发现教材设置的问题情境在生活中随处可寻,习题设置的情境也是丰富多彩。再从近几年高考试题分析,考查动量这部分知识时,问题情境都来源于生活和教材。
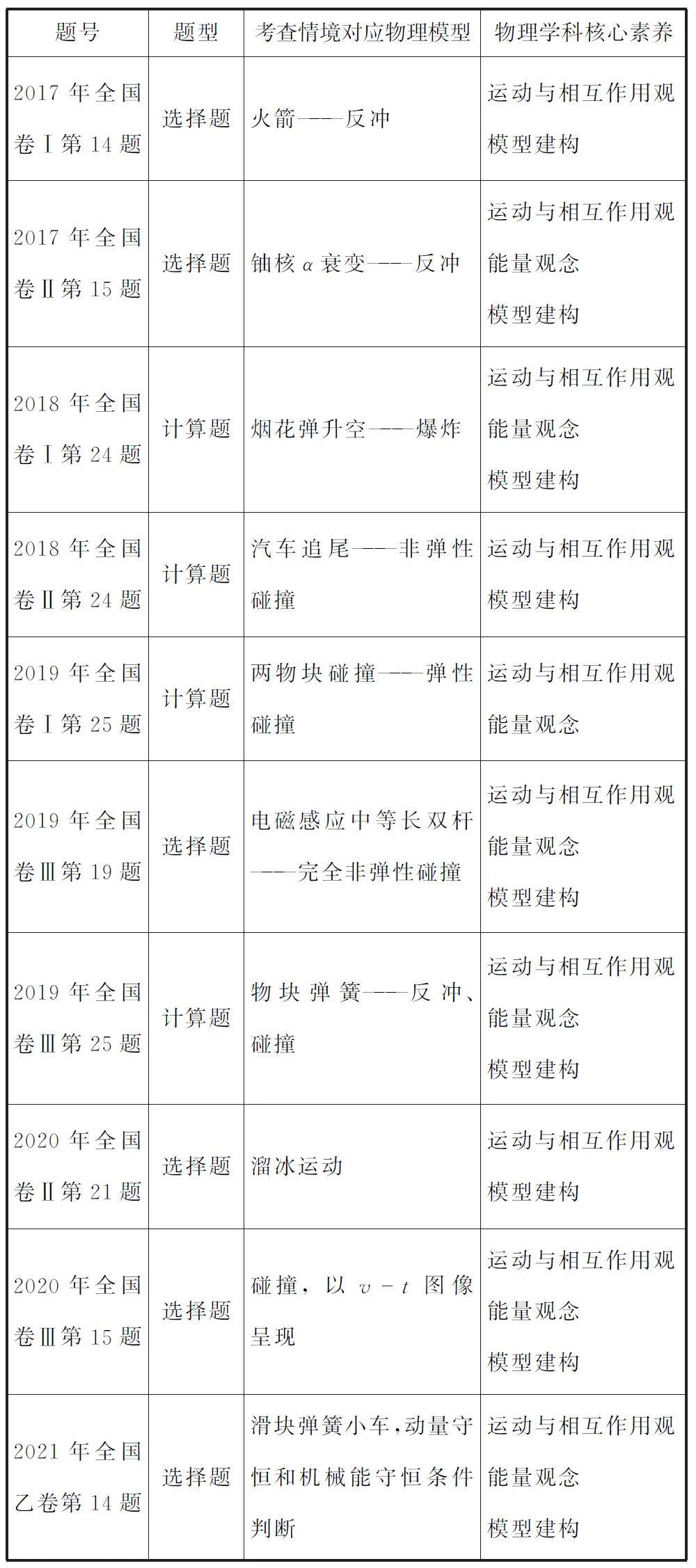
表1 近几年动量守恒考查情况分析
解决这些问题的思路可以归纳为以下思维流程:

图1
三、物理模型归类及应用
物理学科难点之一在于将问题情境转化为模型。针对动量守恒定律这一章节的特点,笔者认为在这一单元复习时应该注意引导学生总结、归纳、对模型进行分类。以下笔者介绍在一轮复习中,通过引导学生对本单元的习题模型进行分类、归纳总结,培养学生建构科学模型能力。笔者认为,这一章节的物理模型总体可以分为两大类:碰撞类和反冲类。以下是笔者引导学生归纳的主要模型。
1.碰撞类
基本模型:物块-物块(小球-小球)

图2
分析:
(1)弹性碰撞
①“两动”
系统机械能守恒:
②“一动一静”
(2)非弹性碰撞
系统能量守恒:
(3)完全非弹性碰撞(碰后粘在一起)
系统动量守恒:m1v1+m2v2=(m1+m2)v共
系统能量守恒:
特点:1.动量守恒 2.速度合情 3.动能不增
此类模型为最基础的模型。
模型:物块-弹簧模型

图3
分析:
①弹簧压缩状态
系统能量守恒:
②压缩最大时
系统动量守恒:m1v1=(m1+m2)v共
系统能量守恒:
③弹簧恢复原长状态
模型:小球冲光滑曲面
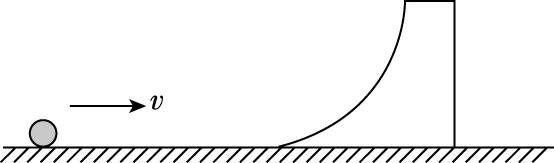
图4
分析:
(1)小球冲至曲面最高处
系统动量守恒:m1v1=(m+M)v共
(2)小球又返回曲面底端
通过对过程分析和列式,引导学生总结:“物块-弹簧模型”和“小球冲光滑曲面”可以归为弹性碰撞模型。
模型:滑块-木板模型
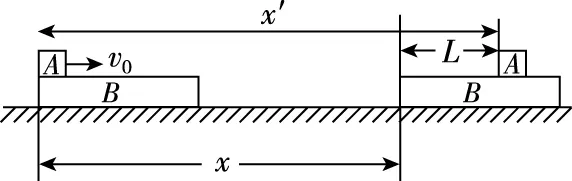
图5
分析:
系统动量守恒:mAv1=(mA+mB)v共
功能关系:Q摩擦热=fs相对=μmg(x′-x)
模型:子弹打木块
(1)子弹留在木块中

图6
分析:
系统动量守恒:m1v1=(m+M)v共
功能关系:Q摩擦热=fd=μmg(x1-x2)
(2)子弹打出木块
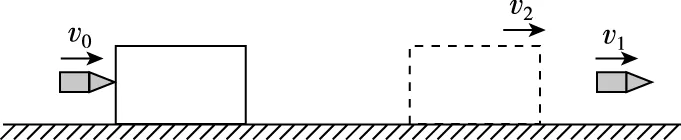
图7
系统动量守恒:m1v0=m1v1+Mv2
功能关系:Q摩擦热=fd=μmgd(d为木块厚度)
模型:电磁感应中双杆模型
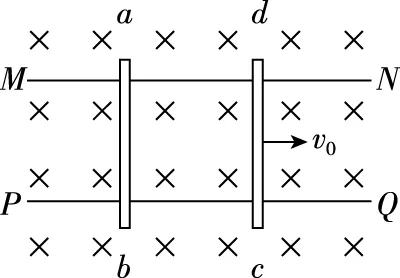
图8
分析:
系统动量守恒:m1v0=(m1+m2)v共
通过过程分析和列式,引导学生总结出:“滑块-木板模型”“电磁感应中双杆模型”“子弹打木块模型(子弹留在木块中)”可以归类为完全非弹性碰撞。
2.爆炸、反冲类
模型:爆炸
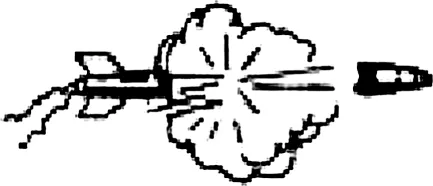
图9
系统动量守恒:Mv0=-mv1+(M-m)v2
系统能量守恒:
特点:1.动量守恒 2.机械能增加 3.爆炸前后位置不变
模型:反冲模型
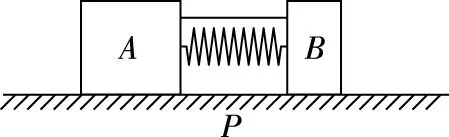
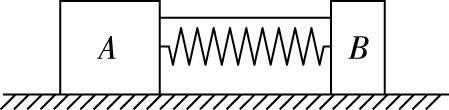
图10
系统动量守恒:0=m1v1-m2v2
变式模型:

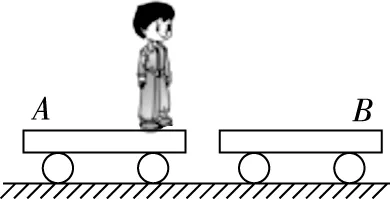
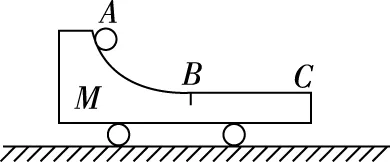
模型:人船模型
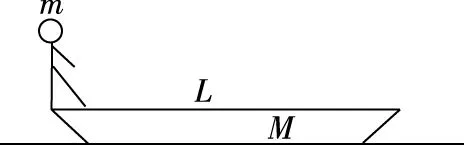
图12
系统动量守恒:
几何关系:
特点:系统水平动量为0,人走船走,人停船停。
变式模型:
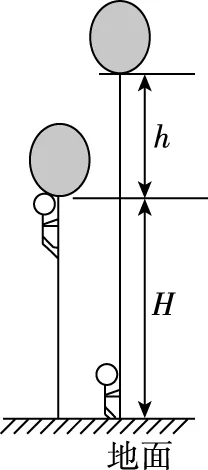
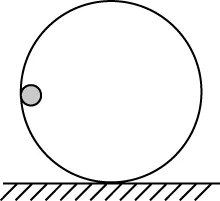
通过对情境与运动过程的分析,引导学生总结“人船模型”及其变式都可以归纳为“反冲模型”
下面我们以具体的两个例题,通过模型识别流程解决两种问题情境。
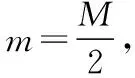
(1)滑块运动过程中,小车的最大速度大小vm;
(2)滑块滑到C端时的速度vC;
(3)滑块从B到C运动过程中,小车的位移大小x。
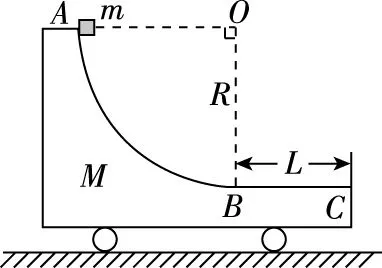
图14
【分析】水平面光滑,系统水平方向上动量守恒。初始时系统m和M均静止,当m向右运动,M向左运动,此模型可以识别为人船模型。人走船走,人停船停,人快船快,人慢船慢。思维分析流程图如下。
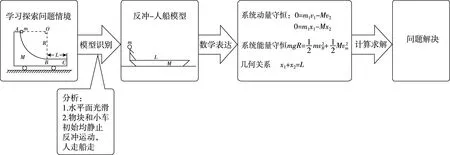
图15
(1)当m运动至B点时m速度最大,则小车M速度最大。
系统动量守恒,向右为正方向有0=mvB-Mvm①
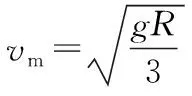
(2)利用人船模型,人减速船减速,再结合能量守恒可得
由系统动量守恒,向右为正方向有0=mvC-Mv2③
由系统能量守恒
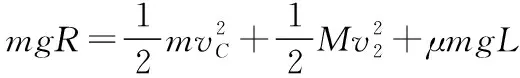

(3)由人船模型,人从船头走到船尾,人与船的位移之和等于船长L,类比从B滑到C时,滑块m的位移与小车位移之和为L。
由系统动量守恒,向右为正方向有0=mx′-Mx⑤
由几何关系得:x′+x=L⑥
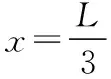
【例2】(2021·广东卷)算盘是我国古老的计算工具,中心带孔的相同算珠可在算盘的固定导杆上滑动,使用前算珠需要归零,如图16所示,水平放置的算盘中有甲、乙两颗算珠未在归零位置,甲靠边框b,甲、乙相隔s1=3.5×10-2m,乙与边框a相隔s2=2.0×10-2m,算珠与导杆间的动摩擦因数μ=0.1。现用手指将甲以0.4 m/s的初速度拨出,甲、乙碰撞后甲的速度大小为0.1 m/s,方向不变,碰撞时间极短且不计,重力加速度g取10 m/s2。
(1)通过计算,判断乙算珠能否滑动到边框a;
(2)求甲算珠从拨出到停下所需的时间。
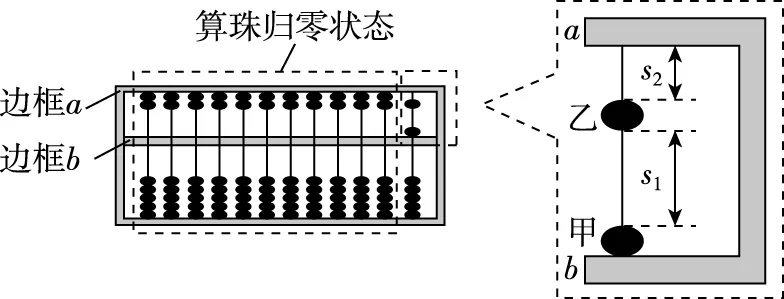
图16
我们通过模型识别思维流程着重解决本例题第1小问。这是一个生活实践问题情境,我们需要从生活现象中识别出物理模型从而解决问题。
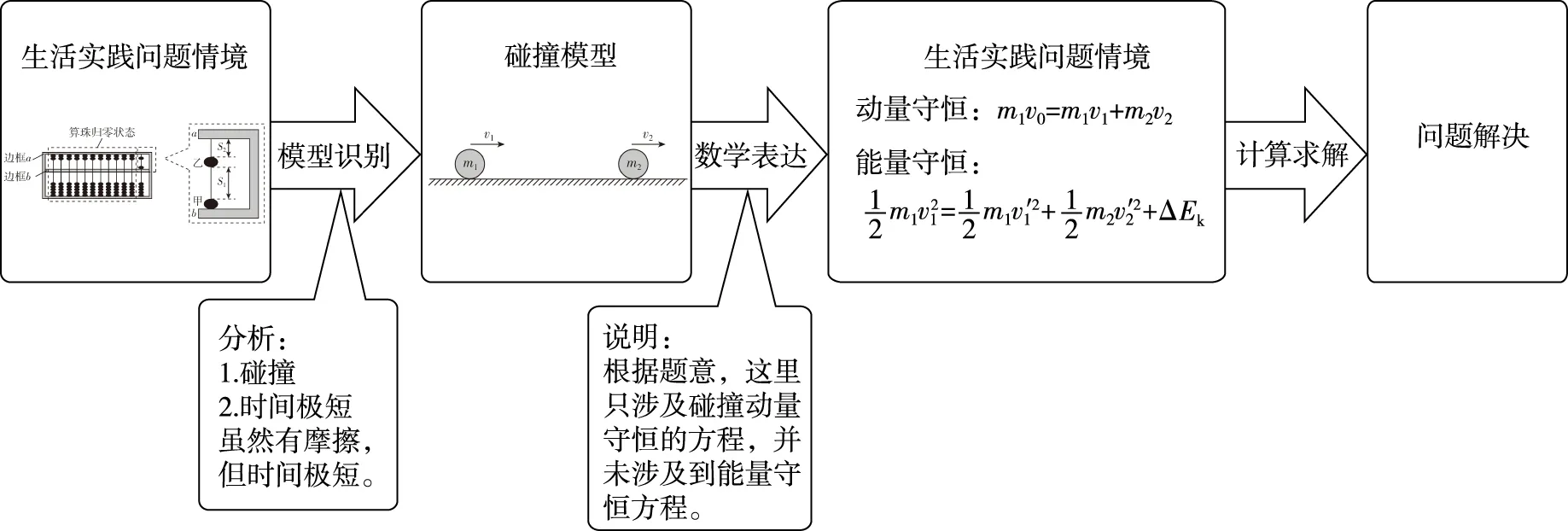
图17
(1)由牛顿第二定律可得,甲、乙滑动时均有
f=μmg=ma①
则甲、乙滑动时的加速度大小均为
a=μg=1 m/s2②
甲与乙碰撞前的速度为v1,则
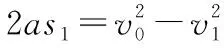
解得v1=0.3 m/s
甲、乙碰撞时由动量守恒定律
mv1=mv2+mv3④
解得碰后乙的速度v3=0.2 m/s
然后乙做减速运动,当速度减为零时则

可知乙恰好能滑到边框a。
通过上面例题,只要学生学会建构动量守恒的几个基本模型,在具体的问题情境中分析一些关键词语,识别出对应的模型,就可以很快列出相应的数学方程解决问题。
四、结语

