基于最优组合模型的中国天然气需求量预测

何润民 王富平， 李洪兵 邹晓琴 王 莅

（1.中国石油西南油气田公司天然气经济研究所，四川 成都 610051；2.西南石油大学经济管理学院，四川 成都 610500）

0 引言

近年来，随着我国经济快速发展，城镇化建设快速推进等因素带来的影响，天然气作为安全高效、绿色清洁的低碳能源，逐渐成为我国实现绿色经济、清洁能源低碳发展的最现实选择。2016年，中华人民共和国国家发展和改革委员会（以下简称“国家发改委”）印发《能源生产和消费革命战略（2016—2030）》［1］，指出要扩大天然气替代规模、充分利用分布式天然气，并实施天然气推广利用重大战略行动。《加快推进天然气利用的意见（2017）》，强调将天然气培育成为中国现代清洁能源体系的主体能源。2019年中国天然气消费量仅占全国能源消费总量的8.1%，由此可见，提高天然气在一次能源消费结构中的占比，是加快构建清洁低碳、安全高效的现代能源体系的重要路径，也是有效治理大气污染，积极应对全球气候变化的有效途径。

天然气市场发展受众多复杂影响因素的制约，各影响因素具有随机不确定性的相互影响，其影响程度较难确定。精准预测中国天然气需求量，为科学施策提供数据支撑，保障重要领域及民生领域的供气安全，科学有效地推进中国天然气发展战略规划设计，在对中国天然气需求量影响因素进行分析的基础上，挖掘有效驱动因素，并据此对天然气需求量进行预测。

1 相关研究现状

迄今为止，国内外学者对天然气需求量的分析及预测进行了多角度的研究，主要集中在以下两个方面。

1）天然气需求量的影响因素。在影响因素方面，柴建等［2］选择了包括人口因素、能源消费结构、国内生产总值、产业结构、天然气产业投资、替代品的市场占有率等因素作为影响天然气需求量的解释变量，对天然气需求量进行分析；邹才能等［3］在基于人工智能与大数据的基础上，为建立油气“安全消费峰值”，综合油气供给结构、油气库存、地缘政治因素、人口规模、进口路径和气候变化等众多因素，对油气需求特征进行分析；蔡流［4］结合产业集中度的指标和协整模型分析表明，对中国天然气需求量产生影响的主要因素包括经济增长、替代能源的价格以及天然气价格；李洪兵等［5］利用逐步回归分析法，按照关联度大小，对GDP、产业结构、消费水平、城镇化率等6个影响因素进行统计显著性检验，并构建函数模型预测天然气未来需求变化趋势；杨俊等［6］采用因子分析方法与回归分析方法对天然气需求量的影响因素进行因子和聚类分析，将其主导影响因素归为消费总量、消费强度以及增长速度；甄仟等［7］采用分解技术方法，识别影响天然气需求量的主要因素有经济发展、天然气管道建设、能源消费强度、管道设施的服务效率以及能源消费结构；高建等［8］运用迪氏对数指标分解法，将天然气需求量驱动因素分解为管网密度、人口城镇化、天然气替代、经济增长、居民天然气气化率、空间扩张、人口密度、能源消费弹性和管道规模，并进行定量分析各效应对中国城市天然气需求量量变动的贡献率；Shahbaz等［9］构建包括资本投资、出口、劳动力影响因素在内的多元框架模型，研究巴基斯坦经济增长对天然气需求量的影响；Zhang等［10］将国内生产总值、城市人口、能源消费结构、工业结构、能源效率以及商品和服务出口，作为解释变量通过贝叶斯模型平均法预测天然气消费量。

2）天然气需求量预测方法。不同的预测方法从不同角度揭示预测对象的演变规律，越来越多的预测方法应用于天然气需求量预测，并得到了较好的实践和发展：王建良等［11］利用筛选出的核心因素，构建分数阶GM（1，3）模型对中国东中西部不同区域的天然气消费需求量进行了预测；李洪兵等［12］运用能源消费弹性系数法对中国未来能源消费趋势进行了预测，并构建消费增量贡献模型预测天然气未来需求量；Szoplik［13］将日历和天气因素纳入建立的多层感知机模型，用于预测一年中任何一天或一天中任何时候的天然气消费量；李洪兵等［14］采用相对关联度分析影响因素与天然气需求量之间的关联程度，并利用双对数函数构建预测模型对川渝地区天然气需求量进行了预测。单一模型存在一定的局限性，组合模型可充分吸纳单一模型提供的有用信息，预测结果精度更高、稳定性更好：马小艳［15］利用DGM（1，1）模型和线性回归模型的优点，将两者融合在一起，建立了DGM（1，1）线性回归组合模型对重庆市天然气消费量进行预测，为解决天然气供给侧问题提供了数据支撑；陈川等［16］构建了BPNNEMD-LSTM组合预测模型，通过与实证研究的对比分析，该组合模型较适合城市天然气短期日负荷需求预测；张吉军等［17］利用结果组合思想，构建了复合权重的天然气需求量组合模型预测天然气未来需求量；Zhu等［18］利用拟合值偏离度倒数法确定单一模型的组合加权系数，构建了残差自回归模型和Kal⁃man滤波算法的组合预测模型，对天然气需求量进行预测分析。

需要注意的是，上述分析国民经济、产业结构、人口、城镇化、能源消费总量、能源价格、能源消费结构、环保政策、气象变化、管道建设、日期等因素，对天然气需求量的影响，并以单一模型或非最优组合模型为主进行天然气需求量预测。未考虑将科技创新、收入水平等作为天然气需求量的解释变量，构建最优组合模型预测天然气需求量。为此，将科技创新和收入水平纳入天然气需求量的解释变量中，采用灰色相对关联度从GDP、产业结构、人口发展、能源消费总量、能源消费结构、环境规制、科技创新、收入水平8个影响因素中，挖掘对天然气需求量影响较大且不存在多重共线性问题的有效影响因素，并将多元线性回归模型与Cobb-Douglas生产函数扩展模型进行融合，建立最优组合模型，对天然气需求量进行预测。

2 相关方法原理

2.1 灰色相对关联度

灰色理论早已应用于天然气消费量预测［19］，而灰色相对关联度是灰色关联分析的一种重要方法，其基本思想是根据数据序列之间几何曲线发展变化趋势的紧密程度判断数据序列的关联程度［20］，克服了传统概率统计需要大量的某一特殊规律数据的不足。运用灰色相对关联度选择天然气需求量影响较大的因素，作为自变量预测天然气未来需求量。灰色相对关联度计算步骤如下：

1）设长度相同，且初始值非零的数据序列为：

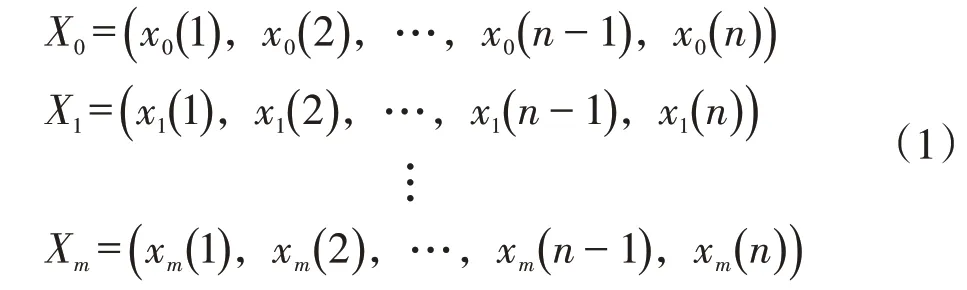
2）计算Xi数据序列的初值像序列X*i，即：

2.2 灰色Verhulst模型

采用对非单调的摆动发展数据序列预测性能较好的灰色Verhulst模型，预测2020—2025年天然气需求量影响因素指标值，为多元线性回归模型和Cobb-Dauglas生产函数扩展模型预测天然气需求量提供基础数据。灰色Verhulst模型［19］构建过程如下：

2.3 多元线性回归模型

回归分析是刻画客观事物之间具有存在和发展的内在规律的回归函数，由英国生物学家和统计学家高尔顿（Francis Galton）于19世纪末在研究遗传学特性时首次提出来的。计量经济学理论定义回归函数为：被解释变量Y的条件均值表现为解释变量X的函数，即

式（8）是以条件均值表现的回归函数E(Y|Xi)刻画随着解释变量的变化，被解释变量的平均变化。在复杂的天然气需求量预测系统中，将描述一个被解释变量与多个解释变量之间线性关系的回归函数称为多元线性回归模型，一般形式为：

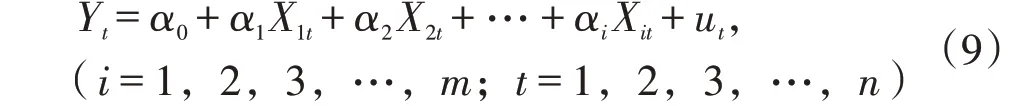
其中，Y t为第t时刻的被解释变量，X it为第t时刻的第i个解释变量，α0为截距系数，αi为斜率系数，ut为随机误差项（一般假定随机误差项期望值为零）。利用最小二乘法估计模型参数α0与αi的值。

2.4 灰色GM（0，N）模型

灰色GM（0，N）模型可用于具有多个自变量的天然气需求量预测之中，其建模过程如下：为GM（0，N）模型。其中，-a为系统发展系数，bi为驱动系数，b i x(i1)(k)为驱动项。

2.5 最优组合预测模型

组合预测模型就是将两个及以上的单一预测模型进行融合，充分利用单一预测模型提供的有用信息，达到进一步降低预测误差平方和的目的。预测误差平方和反映了预测值离散程度的状况，其值越小则表明预测模型的拟合预测性能越好，反之越差。以组合预测误差平方和为目标函数，通过使组合预测误差平方和达到极小来确定组合预测模型的权重系数。若对同一预测对象有N种单一预测模型，则组合预测模型为：

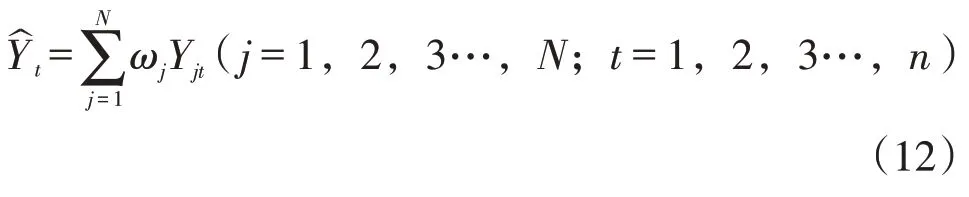
其中，为组合预测模型第t时的预测值，ωj为第j种单一预测模型的权重系数，Y jt为第j种单一预测模型第t时的预测值。

组合预测模型的预测误差为et，则

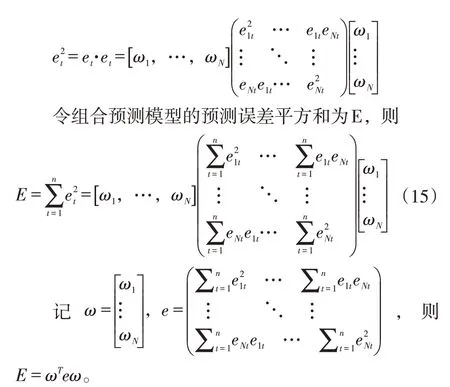
令P为分量全是1的向量，即P＝［1，1，…，1］T。则约束条件可表示为：

满足约束条件式（17），使E达到最小的最优权重系数向量为：

其中，e-1为e的逆矩阵。

3 挖掘有效的天然气需求量影响因素

通过对历史文献的全面综合分析和归纳总结，初步将GDP、产业结构、人口发展、能源消费总量、能源消费结构、环境规制［21］、单位能耗、收入水平8个影响因素作为中国天然气需求量的解释变量，探讨其对天然气需求量的影响。

2000—2019年的天然气需求量影响因素各指标均来源于中华人民共和国国家统计局（以下简称“国家统计局”）；2000—2017年天然气需求量数据来源于国家统计局，2018—2019年天然气需求量数据来自于国家发改委公布数据整理所得，天然气影响因素指标及其需求量数据如表1所示。其中，天然气影响因素GDP、产业结构、人口发展、能源消费总量、能源消费结构、环境规制、单位能耗、收入水平 等 解 释 变 量，分 别 用X1、X2、X3、X4、X5、X6、X7、X8表示，单位分别为万亿元、%、亿人、108t标准煤、%、亿元、m3／百元、万元；全国天然气需求量用Y表示，单位为108m3。

表1 天然气需求量影响因素指标及其需求量统计表

首先，利用灰色相对关联度模型计算天然气需求量与各影响因素之间及两两影响因素之间的关联度值，结果如表2所示。因0.5＜r0i≤1，故设定灰色相对关联度r0i＜0.51时，表明该影响因素对天然气需求量的影响程度极小，可剔除该解释变量；设定两两影响因素之间的灰色相对关联度大于0.85时，表明该组影响因素存在线性关系或接近线性关系，可剔除与天然气需求量关联度较小的解释变量。

因此，由表2不难看出，解释变量X2与被解释变量Y之间的灰色相对关联度为0.506 4，小于0.51，关联程度较低，可剔除解释变量X2；从表2可以发现：影响因素X1、X3、X4、X5、X6、X7、X8与天然气需求量Y之间的灰色相对关联性较强，初步考虑作为解释变量。

表2 灰色相对关联度表

其次，将初步筛选出来的解释变量进行两两分组，发现影响因素X4与X5相互之间的灰色相对关联度分别为0.868 7，大于0.85，它们之间存在线性关系或接近线性关系，需要剔除其中两个解释变量；另一方面，影响因素X4、X5与天然气需求量的灰色相对关联度r04＝0.664 0＞r05＝0.621 0，由于解释变量与被解释变量的关联程度越高越好，故剔除解释变量X5。

最后，筛选与天然气需求量关联程度较高的影响因素，同时剔除存在线性关系或接近线性关系的影响因素之后，最终确定Y的解释变量为X1、X3、X4、X6、X7、X8。

4 天然气需求量预测

4.1 建立基于最优权重系数的天然气需求量组合预测模型

根据式（9）和式（10），利用被解释变量Y与确定出的解释变量X1、X3、X4、X6、X7、X8，建立多元线性回归模型Y1和灰色GM（0，N）模型Y2，再以预测误差平方和最小为目标函数，将多元线性回归模型Y1和灰色GM（0，N）模型Y2进行融合，构建最优组合预测模型Y，预测的拟合结果如表3所示。则多元线性回归模型和灰色GM（0，N）模型的拟合平均相对误差分别为2.073 9%、1.934 3%，一般来说，平均相对误差值小于10%，模型预测精度为“优”［11］，表明该模型可作为组合预测模型的单一预测模型。根据式（17），确定以预测误差平方和最小为目标函数的最优组合权重系数分别为：ω1＝0.821 3和ω2＝0.178 7。

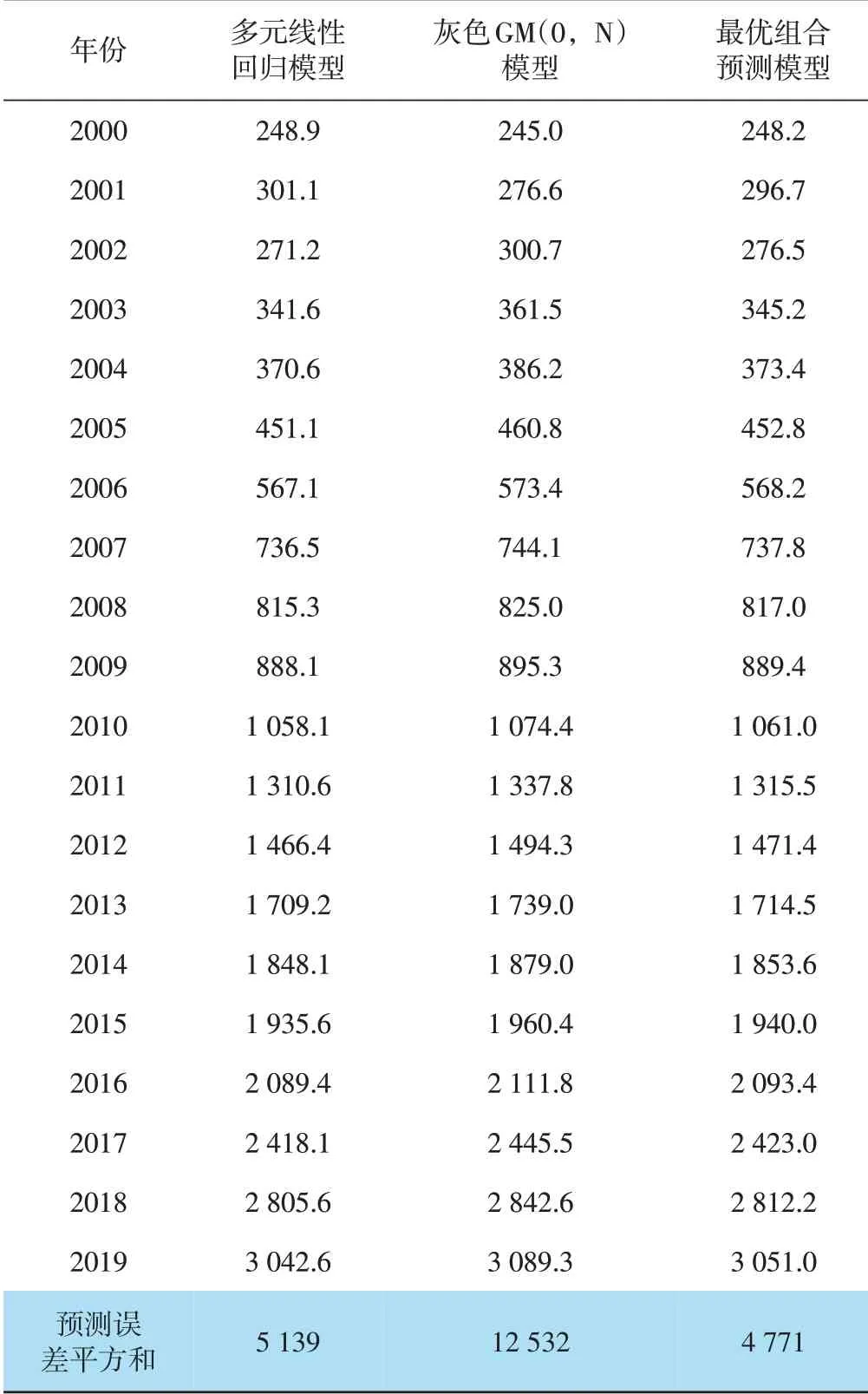
表3 天然气需求量的拟合值统计表 单位：108m3

由式（12）可得最优组合预测模型为：

天然气需求量实际值与最优组合预测模型拟合值的对比情况如图1所示。

图1 中国天然气需求量预测图

4.2 最优组合模型的天然气需求量预测

被解释变量需要在相关解释变量已知的情况下进行预测，采用预测性能较好的灰色Verhulst模型对2021—2025年的各影响因素指标进行预测，预测结果如表4所示。

表4 各影响因素指标预测结果表

分析图1可知，以有效驱动因素构建的最优组合模型可实现拐点预测，具有非线性逼近预测功能。由表3可知，最优组合预测模型的误差平方和比多元线性回归模型和灰色GM（0，N）模型的误差平方和分别减少了368、7 760，表明该最优组合预测模型对天然气未来需求量预测具有较强的说服力。因此，以最优组合预测模型预测出的2021—2025年中国天然气需求量如图1所示。

由图1分析可知，2020年受新冠肺炎疫情影响，天然气提前实施淡季价格支持复工复产，其需求量仍保持较高增速。2021—2025年中国天然气需求量年均增速由近6年的10.28%降至6.79%，且天然气增长率呈下降趋势，表明中国天然气需求量的增速有所减缓；随着中国经济的高质量发展、人口数量稳步增长、收入水平的不断提高，中国天然气需求量仍呈增长趋势，到2025年中国天然气需求量将达到4 548×108m3。

5 结论

深入分析了天然气需求量的影响因素并在此基础上对天然气需求量进行预测，不仅是相关部门制定能源体系发展政策的基础，也是建立天然气供需预测预警机制的内在需求。采用灰色相对关联度模型分析天然气需求量背后的驱动因素，然后挖掘出对天然气需求量影响较大且不存在共线性问题的有效因素作为解释变量，并据此建立最优组合预测模型，对中国天然气需求量进行预测。主要结论如下：

1）灰色相对关联度模型分析结果显示：对中国天然气需求量影响程度从高到低排列的因素依次为GDP、收入水平、能源消费总量、能源消费结构、环境规制、单位能耗、人口发展、产业结构；根据影响因素与天然气需求量的关联程度以及因素之间是否存在多重共线性问题，最终挖掘出GDP、收入水平、能源消费总量、能源消费结构、单位能耗、人口发展6个有效影响因素作为解释变量，其中GDP、单位能耗对天然气需求量具有正向驱动效应；GDP增长对天然气需求量增长贡献最大，控制GDP高质量发展速度可有效控制天然气需求量增长速度。

2）以预测误差平方和最小为目标函数，构建的最优组合预测模型比单一预测模型的拟合误差平方和降低了7.15%～61.92%，表明该最优组合模型具有很好的预测性能。基于该组合模型的预测结果表明，2021—2025年中国天然气需求量仍呈持续上升趋势，但随着科学技术的不断创新、能源发展迈入提质增效新阶段、中国经济进入高质量发展新时代阶段，天然气需求量增速有所降低，天然气市场将由快速发展向稳定发展转变。对天然气需求量的预测，为加强天然气市场的监测和预判提供了科学依据，为建立天然气需求侧管理和调峰机制提供了数据支撑，为实现天然气供需动态平衡提供了重要参考。