非线性回归模型误差方差的经验似然估计*

胡学叶，张正家

（广西师范大学数学与统计学院，广西 桂林 541004）

0 引言

经验似然是由Owen[1-3]提出的一种非参数统计推断方法,具有构造的置信区间域保持性、变换不变性等优点,应用于各种统计模型中。石坚[4]研究了线性模型误差方差的经验似然估计。非线性回归模型是统计学中最基础的模型之一,是线性回归模型的推广,有诸多研究成果。Jennrich[5]和Wu[6]利用最小二乘法给出了非线性回归模型参数估计并证明估计量的渐近正态性。考虑到非线性回归模型广泛应用在各个行业中,本文利用经验似然方法获得了在设计矩阵为非随机的情形下非线性回归模型误差方差的经验似然估计,并证明了估计量的渐近正态性。通过数据模拟发现,经验似然方法得到的渐近方差比传统残差平方和方法得到的估计更小。

考虑非线性回归模型

其中f是一个已知的回归函数,x∈Rp是固定设计矩阵,Y∈R1是响应变量,β∈Rk是参数向量,e∈R1是不可观测的随机误差。设有来自模型的独立同分布样(x1,Y1),…,(xn,Yn),其中xi=(xi1,…,xip)Τ,相应地有一组不可观测的随机误差e1,…,en,使得Yi=f(xi,β)+ei,1≤i≤n。记x(n)=(x1,…,xn)Τ,Y(n)=(Y1,…,Yn)Τ,e(n)=(e1,…,en)Τ。

我们的目的是得到误差方差σ2的估计量,由于e(n)不可观测,需要先对β进行估计。采用最小二乘法,即求的极小值点。

对Qn(β)关于β求导,得到

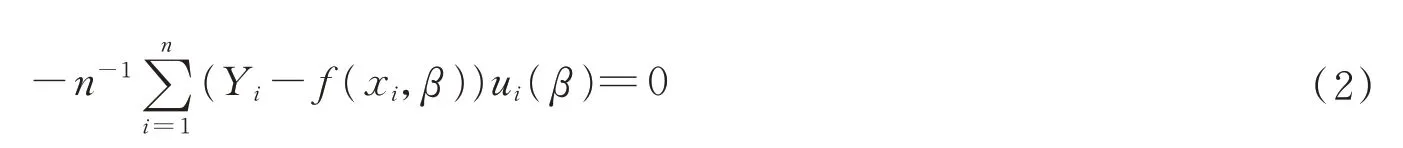
其中ui(β)=∂f(xi,β)∂β,由于上式没有显示解,我们采用牛顿迭代方法求解,得到满足(2)式的为β的最小二乘估计。具体操作如下：

(2)令β新 的 估 计 为,其 中A是n×k的矩 阵,uij是A的(i,j)元素,且uij=∂f(xi,β)∂βj;

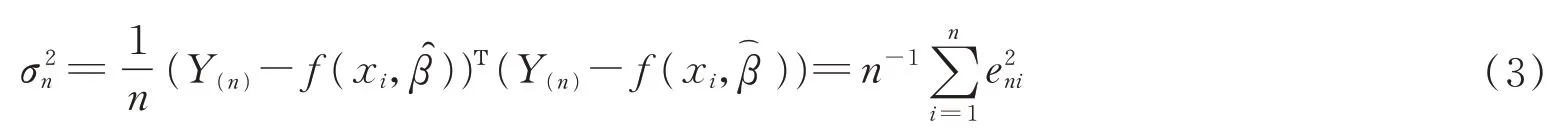
由拉格朗日数乘法得到：

其中λ满足：

因此可以得到误差方差σ2的一个修正估计

（A1）e1,…,en是独立同分布的随机变量,且;存在ε>0,使得,记=μj,j=3,4;

（A2）对每一个x∈τ,函数f(x,β)关于β有连续的二阶导数,β∈Γ,其中τ={x:x∈Rp},Γ={β:β∈Rk},且τ和Γ是紧集;

（A3）对每一个x∈τ,β在真实值某领域内,有是有界的,即,其中ui(β)=表示欧式模;

（A4）存在正定矩阵V,使得当n→∞,有，其中ui(β)=(ui1(β),ui2(β),…,uip(β))Τ;

（A5）存在常数C>0,使得,其中σ2未知,;

注1：为叙述方便,始终假设C表示一不依赖于n的大于0的常数,且C每次出现可以取不同的值。

1 主要结论

定理1若条件（A1）~（A6）成立,当n→∞,有

且

由定理1知，经验似然得到的误差方差的渐近方差比传统残差平方和得到的渐近方差小。

2 模拟结果

表1 估计量的偏差,方差和相对效率(e1∼N(0,1))

表2 估计量的偏差,方差和相对效率(e1∼exp(1)-1)

3 定理的证明

引理1设W1,W2,…,Wn为独立同分布的随机变量序列,若存在α>0,使得,则有

证明：见Ghosh等[7]的引理3。

引理2若条件（A1）~（A6）成立,则有：

其中μj=,j=3,4。

证明：(11)式的证明。满足(2)式，

(12)式的证明。令,由引理2得。且

(13)式的证明。因为

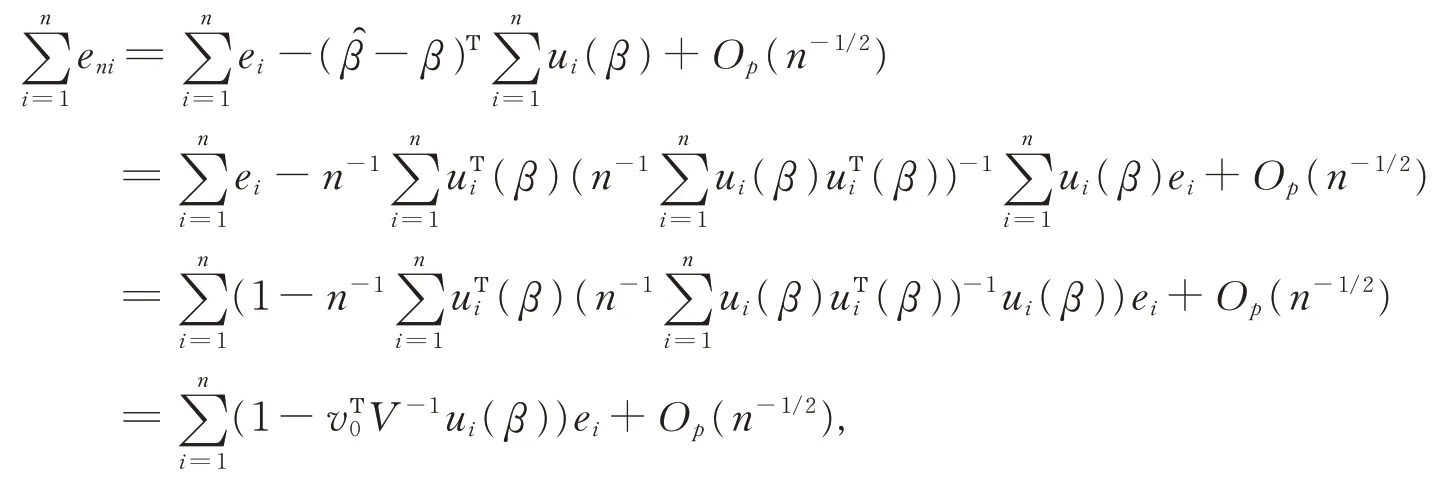
由独立随机变量求和的矩不等式得到

(14)式的证明。令,有

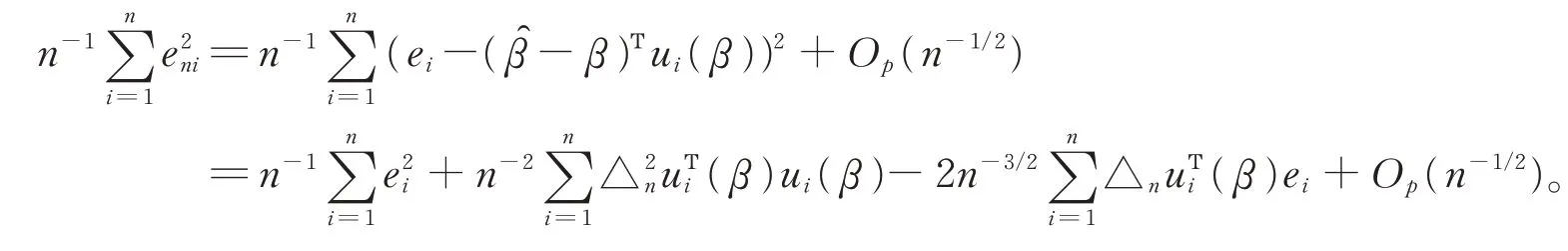
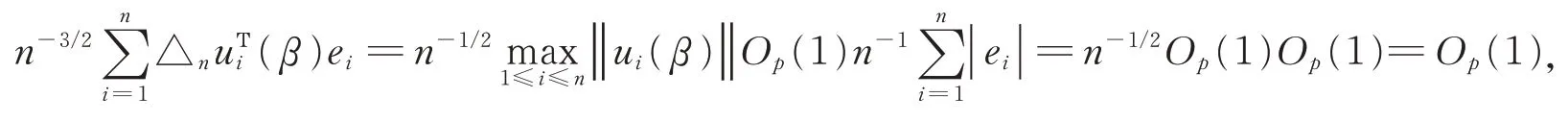
(15)式的证明。由(6)式得。

令ζi=λeni,那么,,即。

定理1 的中(8)式的证明。

定理1中(9)式的证明：