基于深度强化学习的机器人推拨优化装箱问题研究

张浩东，吴建华

上海交通大学，上海 200241

0 引 言

随着机器人技术的发展，机器人在仓储自动化领域得到广泛的应用，用机器人代替工人完成重复繁琐的工作，大大提高了生产效率.其中一个重要应用就是机器人的打包装箱.这项工作通常需要将一定数量的物体装进一个容积有限的箱子中，在这个过程中需要利用视觉技术获取物体信息，并用合适的算法规划物体位置，还要考虑机器人的轨迹、操控等问题.

三维装箱问题是一个组合优化问题，这是一个典型的NP完全问题.MARTELLO等[1-2]提出运用分支边界的方法得到精确解来解决这类问题，DEN[3]和CRAINIC[4]在他的工作基础上做了进一步的研究.精确解虽然能得到非常好的效果，但对于NP完全问题，在维数增加时不能保证能在有限时间内得到解.因此在复杂情况下，使用启发式算法在较短时间内寻找局部最优解是更好的解决方法.VOUDOURIS[5]提出GLS算法通过最小化目标函数来改进物体的放置位置，WANG等[6]提出两种自然启发式算法，DBLF(deepest bottom left fill)算法和MTA(maximum touching area)算法.WANG等[7]针对DBLF的不足做出了改进，提出关注物体占据体积的HM高度图最小化算法，使物体放置位置更加合理，可以为之后的物体留出放置空间.

近年来，随着计算机算力的提升，深度学习发展迅速，传统的强化学习方法与深度学习结合，大大增强了学习效果，在机器人领域得到广泛应用[8-9].许多人开始应用强化学习来解决装箱优化的问题.CHU等[10]提出一种名为Repack的方法，在二维平面上应用强化学习将相同的几何体密集排布在一个矩形框内.ZHU等[11]提出一种两步混合启发式算法，通过强化学习解决二维带包装问题.KUNDU等[12]提出一种Deep-Pack方法，基于Double-DQN的强化学习框架通过视觉信息输入解决二维在线包装问题，并且该方法可以很容易扩展到三维上.HU等[13]针对真实应用场景中的一个运输包装问题，运用强化学习方法提出了一种TAP-Net来解决此类问题.

这些方法主要解决装箱过程中物体放置位置的规划问题，但在实际操作中，机器人在抓取、识别和放置时的误差和不确定性会导致最终结果与规划结果存在误差，在规划过程中为防止物体间的碰撞、重叠也无法做到物体紧密接触.由于机器人操作限制，规划的部分位姿不可行，只能将物体从更高处落下或者将物体放在最优位姿的附近.最终导致空间的浪费.

机器人的推动是一种非抓取操作.非抓取操作如推动、滚动和投掷等通常要比抓取操作困难的多.抓取操作可以通过形封闭、力封闭等方法判断抓取的质量.而非抓取操作不仅需要考虑物体的形状，还需要考虑物体的动力学参数如质量分布、摩擦力等.而这些参数通常都是未知的.MASON[14]使用投票定理来预测由点接触推动的物体的旋转和平移.LYNCH等[15]还提出一种物体接触时的稳定推动方法.但这些方法通常需要强有力的假设如均匀摩擦系数、均匀质量分布等.为解决这个问题，许多人开始使用统计学习的方法.BYRAVAN等[16]通过深度学习方法预测刚体运动，可以预测出机器人完成某个推动动作的结果.ZENG等[17]通过强化学习实现抓取和推动的协同策略.

本文主要关注对于已经放入箱子中的物体，如何通过机器人的推拨动作对物体进行归集、压缩，以腾出更多空间.减少由于机器人操作限制、机器人操作不确定性和规划误差所带来的空间浪费.通过深度强化学习方法，从数据中学习推拨的最优策略，避免了分析方法需要强假设的问题.使用启发式算法评价推拨动作的好坏.将采用推拨动作优化后的装箱结果与直接装箱的结果进行对比，结果证明学习到的推拨策略可以对物体进行归集，减少操作与规划误差带来的影响，提高空间利用率.

1 问题描述

1.1 推拨优化装箱问题

对于一个已知大小的箱子C和N个需要被装入箱子的物体，用机器人将N个物体依次装入箱子中，使用推拨动作归集、调整箱子内物体，优化物体放置位置，使空间利用率最大.假定在装箱前需要装箱的物体模型和装箱顺序未知，因此只需要关注优化当前状态，不需要考虑之后需要放入的物体的影响，因此该问题可以分解为N个子问题，即将用机器人将某个物体装入箱子中并用推拨动作归集、调整当前物体，优化物体的放置位置，使当前空间利用率最大.

1.2 启发式算法装箱评价

装箱问题是一个NP完全问题，直接以空间利用率为优化目标难以得到问题的解，因此通常采用启发式算法评价物体放置位置的好坏，得到局部最优解.在本问题中，使用经典的DBLF算法计算箱子内物体放置位置分数，分数越低代表放置位置越好，因此问题的优化目标变为用机器人将某个物体装入箱子中并使用推拨动作优化，使当前物体放置位置分数和最小.

在t时刻，箱子内有n个物体，每个物体的放置位置为Pi，对应的分数为Si，当前放置位置分数的和为：

(1)

对于箱子内的所有物体，在保证物体在空间上不发生重叠的情况下，存在一组放置位置P=(P1,…，Pn)使得放置位置分数和最小，设这个最小分数为Sbest，学习的目标为使用推拨动作使当前放置位置分数的和接近最小分数Sbest.

使用网格搜索的方式寻找物体的最佳放置位置.在放置物体时首先需要得到箱子内自上而下的高度图Hc和被放置物体自下而上的高度图Hb.物体的每一个放置姿态都可以得到一张高度图，为了简化问题，固定俯仰和翻滚角角度不变，将偏航角360°平分16份，搜索16个角度下的放置位置.

对于箱子中每一个位置，可以通过高度图计算无碰撞情况下的最小高度Z：

(2)

其中(x,y)是高度图像素坐标，(w,h)是Hb的维数.这样我们得到了所有可行放置位置，之后根据启发式算法计算每一个位置的分数，最小分数所对应的坐标就是最优的放置位置.

2 强化学习算法实现

2.1 深度Q网络算法

Q-learning算法是强化学习中的经典算法，通过建立状态动作价值表，寻找每个状态下的最优动作，并根据奖励不断更新表中的期望价值.Q-learning算法中的Q函数通常用表格形式表示，状态空间和动作空间是离散的，并且维数较小.随着人工神经网络技术的发展，人们用人工神经网络拟合Q函数，代替原先的Q函数表格，并用经验回放的方法对网络进行训练.这种方法被称为DQN(deep Q network)算法.

将本问题看作一个马尔科夫决策过程(S,A,P,R)，S为状态空间，A为动作空间，P为状态转移概率函数，R为奖励函数.在t时刻，机器人通过箱子上方的相机得到箱子内物体的状态st，并根据策略π，选择执行动作at，执行动作后状态st根据状态转移概率函数变为st+1，并获得奖励R.我们通过函数Q估计每个状态下执行动作所获得的未来奖励.通过策略函数π选择Q值最大的动作.

π=argmaxa∈AQ(st,at)

(3)

训练的目标是通过迭代最小化|Q(st，at)-yt|获得使R最大的Q函数.其中目标yt为

yt=R(st+1,at)+γQ(St+1,π(st+1))

(4)

Double DQN和Dueling DQN是2种针对DQN算法的改进方法[18-19].普通DQN算法在选择动作和迭代更新中都使用最大Q值，这会导致对Q值的过估计.Double DQN采用2个完全相同的网络结构，评价网络用于选择动作，目标网络用于迭代更新Q值，将动作的选择和Q的计算更新解耦，解决了过估计的问题.

Dueling DQN从网络结构上改进了原有算法，将网络输出的Q函数拆分成了价值函数V和优势函数A，价值函数只有状态有关，表示状态本身的价值，优势函数和状态和动作都有关，两者相加输出得到Q函数，如下所示：

Q(s,a)=V(s)+A(s,a)

(5)

改进后的网络每次训练不光会更新动作价值还会更新状态价值，加快学习速度.

2.2 奖励设计

我们使用DBLF启发式算法评价箱子内物体放置的好坏，DBLF算法公式如下：

位置分数=Z+c(X+Y)

(6)

其中c为一个较小的常量，X、Y和Z为物体中心的坐标，该算法更倾向于将物体放置在更低和X、Y更小的位置，分数越低代表放置位置更优.我们的训练目标是使当前箱子内物体的放置位置分数最小，设计奖励函数如下：

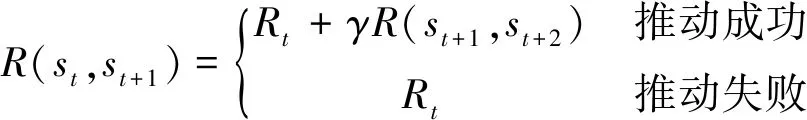
(7)

当推拨动作成功，状态发生改变时，奖励为当前奖励Rt加上未来奖励乘以一个衰减因子γ，当推拨动作失败，状态没有发生任何改变时，奖励为当前奖励，并切断未来奖励.衰减因子表示对未来奖励的关注程度；衰减因子越大，学习过程越关注未来可能获得的奖励大小；衰减因子越小，学习过程会更加关注当前动作奖励的大小.当前奖励函数如下：

Rt=Rp(st,st+1)+Rs(st,st+1)

(8)

其中Rt(st,st+1)表示推拨动作奖励，Rs(st,st+1)表示状态变化奖励，其中推拨动作奖励如下：

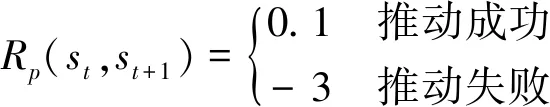
(9)

状态变化奖励如下：

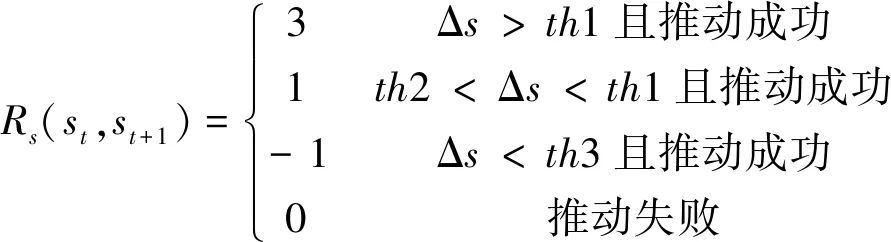
(10)

Δs表示分数变化大小，th1、th2和th3为3个判断阈值.

当推拨动作完成时，奖励增加0.1，以加快学习过程，当推拨动作完成失败，这是我们最不愿意看到的情况，因此奖励减3并切断未来奖励.只有当推拨动作完成时才能获得状态变化奖励.当放置分数降低较小值时通常表示物体在X、Y方向上接近目标，此时奖励增加1.当放置分数降低较大，通常表示物体在Z方向发生改变，如物体从第2层掉落到第1层，我们更倾向于铺满第1层后放置第2层，因此奖励增加3.

2.3 动作空间遮蔽

在学习过程中，需要平衡探索与利用关系，探索是随机执行某个动作，这样可以到更高价值的动作，有利于学习最优策略，但一味地探索得到奖励太低，会使整体奖励受损.利用是根据已有知识选择最优动作，一味地利用有可能陷入局部最优，学习不到最优策略.在探索时,经常会得到一些没有意义的动作，比如对于本问题，过于靠近箱子边缘的动作是不可行的，而远离物体的动作是没有意义的.因此本文采用了HUNDT等[20]提出的方法，对输出的动作空间进行遮蔽，提高探索的效率，进一步提升学习速度.如图1所示，从输出的可视化图像中可以看出，只有在物体周围的像素点有输出，表示只有在这些位置，推拨动作才可能成功.定义一个遮蔽函数M(st，a)，当动作a在状态st下一定失败时，M=0，否则M=1.网络预测的动作空间变为：

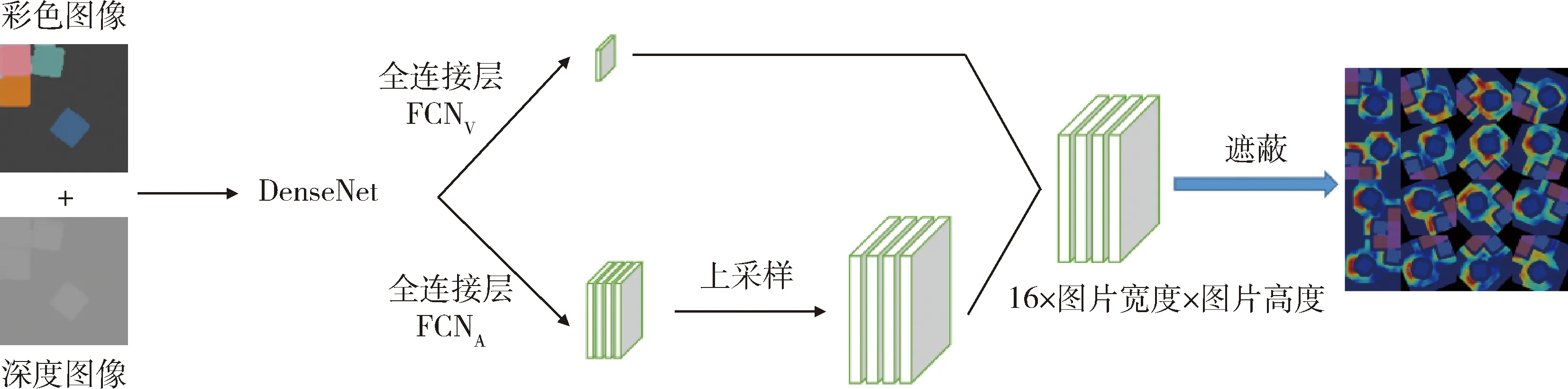
图1 网络结构Fig.1 Network architecture

Mt(A)={a∈A|M(st,a)=1}

(11)

因此选择执行动作时只在可能成功的范围内选择，为了在训练过程中有效利用动作空间的遮蔽，将(4)的目标函数变为：

(12)

其中：

πM(st)=argmaxa∈Mt(A)Q(st,a)

(13)

2.4 状态空间与动作空间表示

将本问题的状态空间定义为箱子内物体的RGB图像和高度图像，在t时刻通过箱子上方的

RGBD相机得到图片信息，将数据转化为三维点云，并在重力方向上投影最终得到RGB图像和高度图像，如图1所示.

将动作空间参数化为X、Y坐标和推动方向，图像每个像素点代表推拨动作起始位置的X、Y坐标，每个坐标包含16个数据，将平面360°平均分成16个推拨动作的方向，推动距离固定为5 cm并且沿直线推动.

2.5 网络结构

网络结构如图1所示.将RGB图像和高度图像合并作为网络输入，通过预训练的DenseNet[21]网络提取特征，根据公式(5)为了得到状态函数输出和优势函数输出将提取到的图像特征输入到2个全卷积神经网络中，每个网络包含2个卷积层非线性层和归一化层.FCNv输出一个一维的状态值，FCNA的输出再经过一层上采样得到与输入相同大小的优势函数，与状态值相加后得到最终的Q函数.

3 仿真学习与实验结果

3.1 仿真环境与学习过程

在Ubuntu16.04系统中使用Coppeliasim仿真软件进行训练和仿真实验.

使用一个大小为22 cm×22 cm×12 cm的盒子作为箱子，需要装入的物体为32个边长为5cm且颜色不同的方块.每次放置时首先得到高度图像，依据式(6)的启发式算法计算一个最优分数，然后在盒子中生成一个随机位置和随机姿态放入方块.当盒子中物体放置分数接近最优分数或者推拨次数大于一定值时，放入下一个方块.直到32个方块均被放入盒子中并且完成推拨动作.

推拨动作用6自由度UR机器人实现，末端执行器简化为一个2 cm×2 cm×h的长方体，实际应用可以使用手爪或吸盘.

3.2 学习结果

本问题的学习过程受物体初始位置影响非常大，比如方块在放置时恰好落入角落中，那么不管怎样推都无法将方块推到最优位置；或者方块恰好掉落到最优位置，那么不需要推就可以放置下一个方块.

从每5000次推动方块动作的平均奖励来观察学习的结果.如图2所示，总体趋势在不断上升并最终趋于稳定，代表学习过程逐渐收敛.

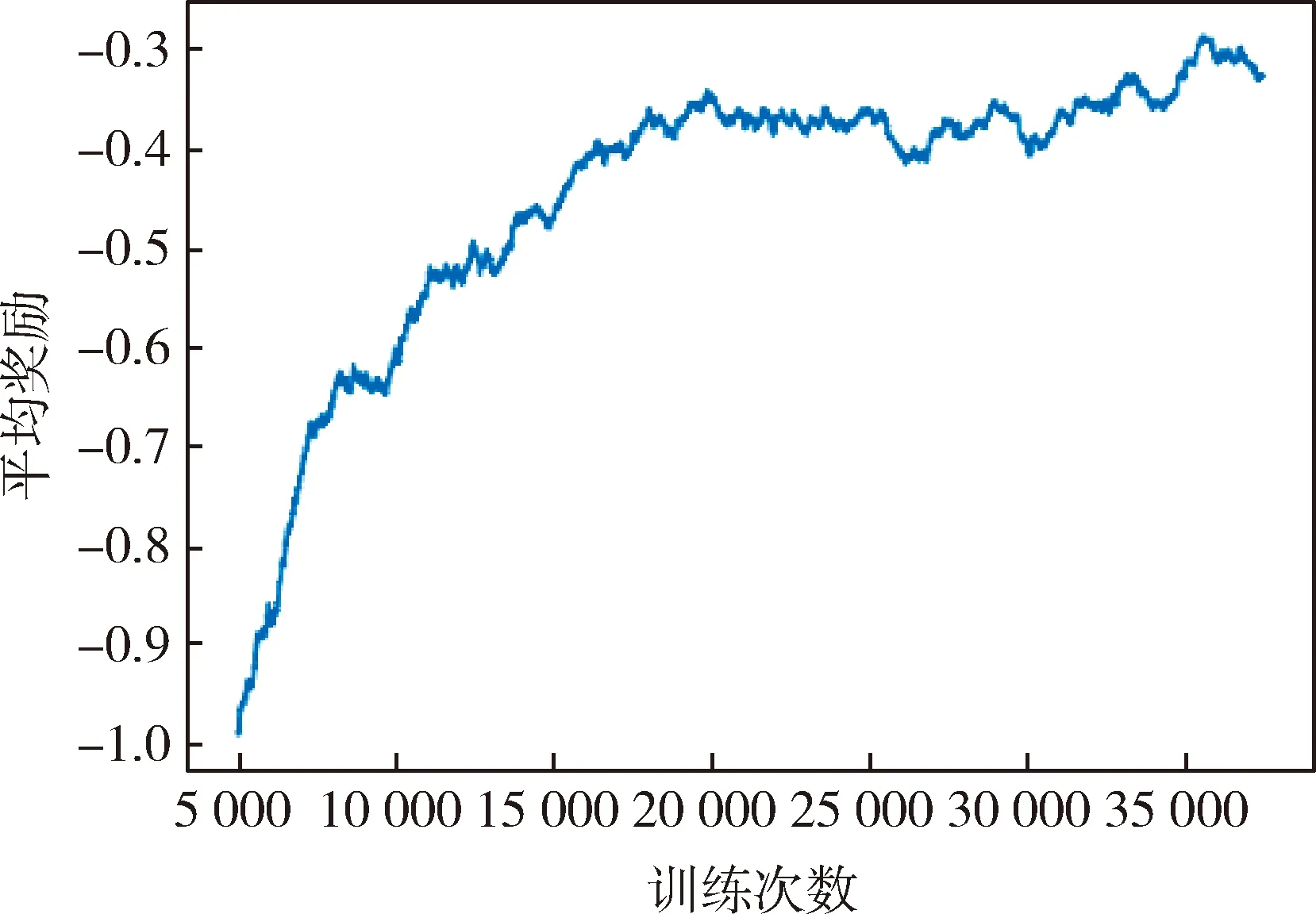
图2 平均奖励曲线图Fig.2 Average reward curve

3.3 实验结果

对比了采用推拨动作优化的装箱结果和直接放置的装箱结果.为模拟实际放置过程中的不确定性误差，人工引入放置误差.

每次放置方块时，首先得到高度图，依据启发式算法计算出最优分数对应的位置，放置时在X、Y方向加入±0.5 cm的随机误差，并使物体从规划位置的上方一定距离落下.

向箱子中装入10个方块，进行10次实验，2种装箱方法分数最低与分数最高的结果如图3～4所示，左边为分数最高的情况，右边为分数最低的情况.由于存在放置误差，方块在放置过程中会出现碰撞、翻滚的情况，在不经过归集的情况下会影响下一个方块的放置.而经过推拨动作优化后，方块可以比较稳定地整齐排列在箱子左下角，即使有碰撞、翻滚的现象也可以将方块推到比较合适的位置.但在最坏情况下，有一个方块下落时斜着卡在箱子与另一个方块当中，学习到的策略没能很好地解决这种情况.

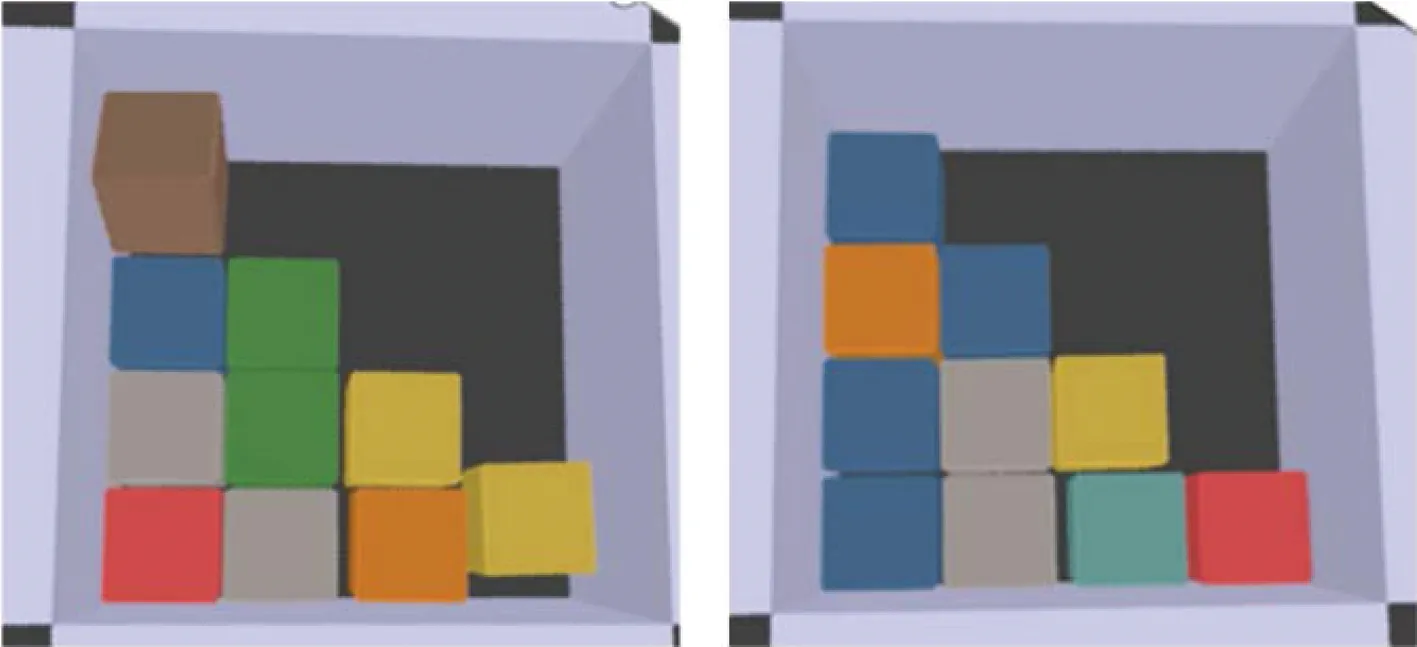
图3 放入正方体并且使用推拨动作优化Fig.3 Packing cubes and optimizing them with push

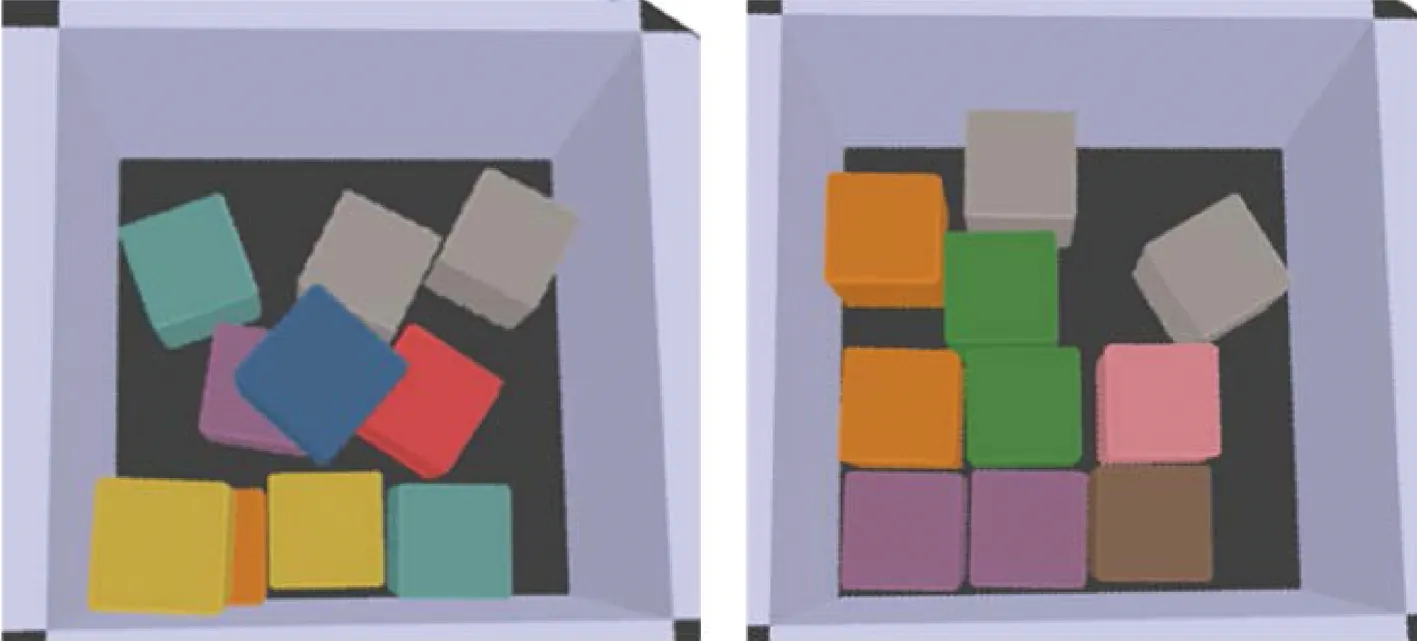
图4 放入正方体不使用推拨动作优化Fig.4 Packing cubes without push

还对比了放入其他长方体的情况.同样实验10次，如图5～6所示.对于长宽高不等的长方体，学习到的策略优化程度有限，经常出现不合理的推拨动作，并且无法将立起来的长方体推倒，但相较于直接放置，还是有明显的提升.

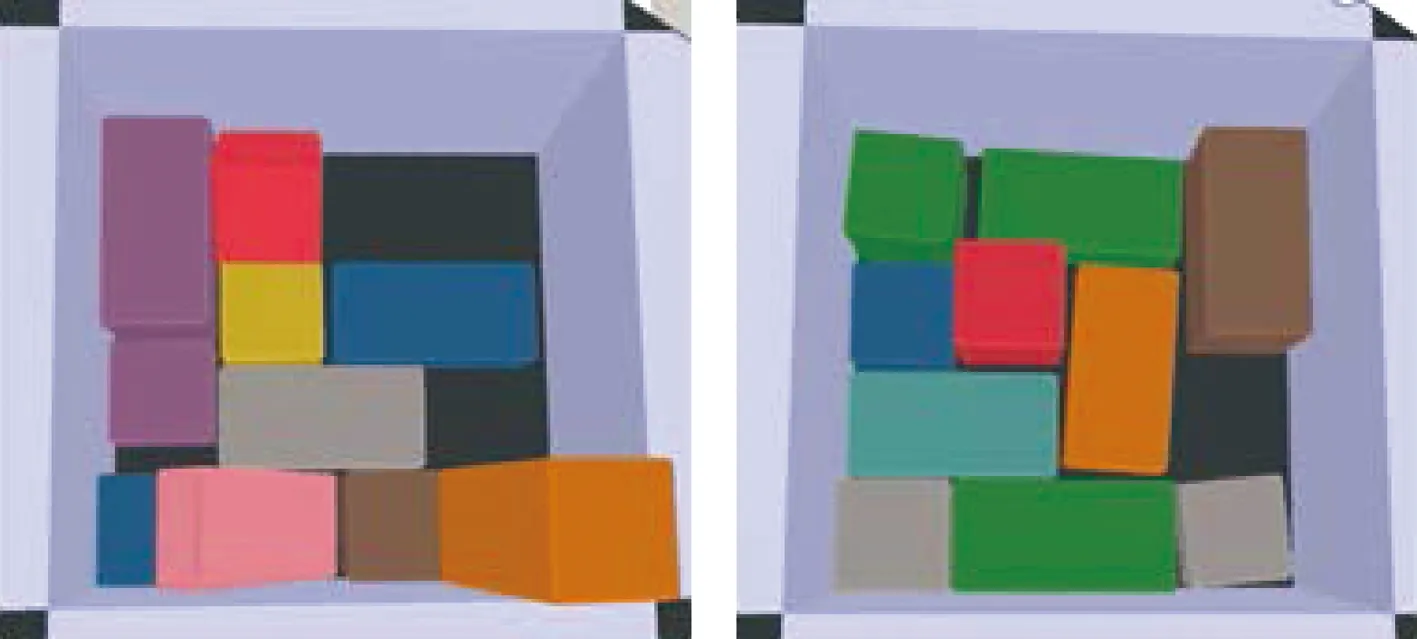
图5 放入长方体并且使用推拨动作优化Fig.5 Packing cuboids and optimizing them with push

2个实验的结果如表1所示，在2种情况下，使用推拨动作优化后物体放置位置分数均降低了24%左右，证明学习到的策略能够一定程度提高装箱的空间利用率.

表1 实验结果Tab.1 Results

在使用推拨动作优化的情况下向箱子中装入32个方块，实验10次.其中有6次32个方块顺利铺满了2层，有4次没能铺满，失败的情况如图7所示.原因主要是学习推拨策略不能很好地解决卡住的方块.并且由于策略为使放置位置分数最小，对于卡在角落里的方块基本不会采取推拨动作，无法将角落的方块向角落里压缩，占据空余的空间，影响了下一个方块的放置.如图7下面两张图所示，由于第2层没有足够的空间，方块被放置在了第3层并被推到左下角.

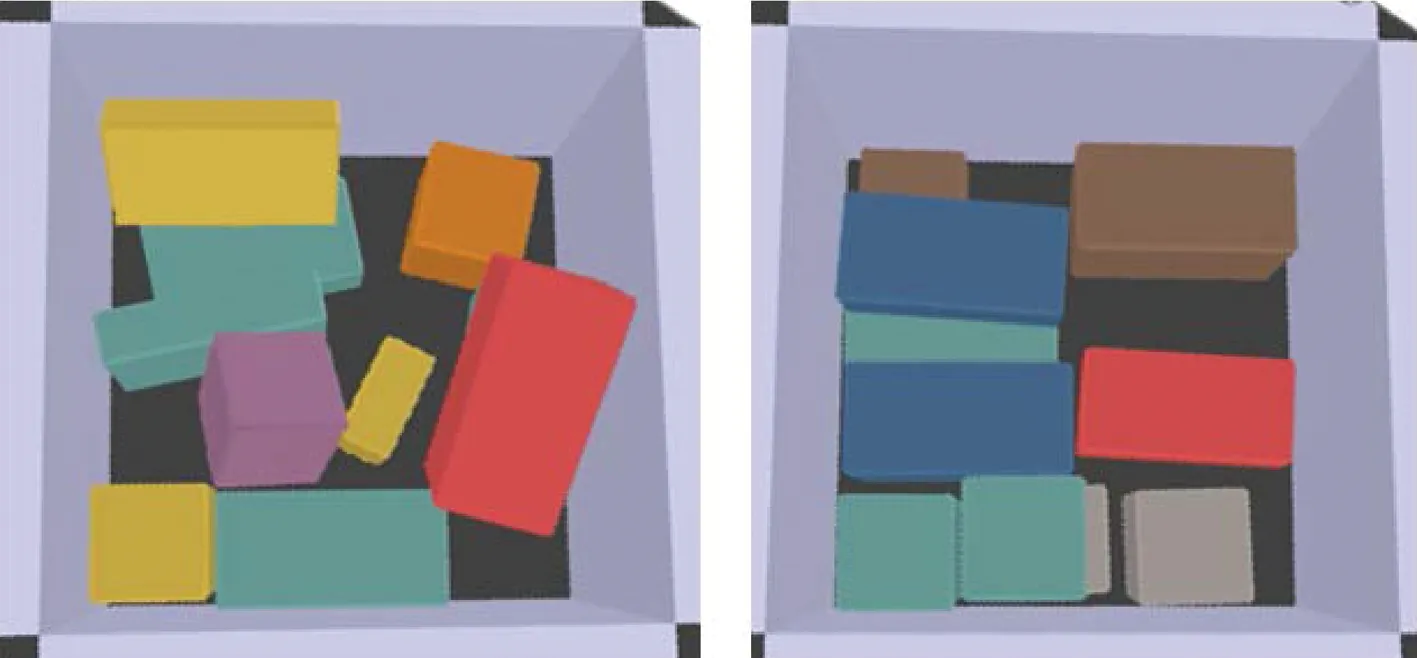
图6 放入长方体不使用推拨动作优化Fig.6 Packing cuboids without push

图7 放入32个正方体失败情况Fig.7 Failures to packing 32 cubes

4 结 论

对于机器人的三维装箱问题，本文解决了在放入物体后对放置位置的重新归集、调整的优化问题，使用深度强化学习的方法训练机器人学习推拨动作策略，以减小放置位置分数为目标在仿真中完成训练和实验，结果表明，学习到的策略可以将箱子中的物体更好地归集到一起，对于正方体和长方体形状的物体都有较好的优化效果.降低了由于机器人操作限制，操作、识别和规划误差带来的影响，相比于直接规划放置物体，经过推拨动作优化后，提高了装箱过程的空间利用率.