面向火星自主漫游任务的视觉-惯性感知系统

贾慎涵，许学成，陈泽希，焦艳梅，黄 煌，王 越*，熊 蓉*

1.浙江大学,杭州 310027

2.北京控制工程研究所,北京 100094

0 引 言

稳定可靠的自主导航系统对巡视器在火星表面执行复杂任务至关重要.巡视器需要在火星表面进行探索并执行一系列复杂科研任务，如果由地面科研人员向其发送控制指令，存在一系列困难：1)信息传输耗时非常多，信息往返往往要几十分钟；2)电信号远距离传输，存在很高的丢失率，并产生很大噪声；3)传输带宽非常有限.受这些因素的影响，要保证火星漫游车的运行安全，只能保持非常低的运动速度，且地面科研人员进行规划控制时，可以使用的信息非常有限.因此，利用火星车搭载的传感器，实现自主漫游，已经成为未来火星探测技术的趋势之一.以美国火星车为例，最新的“毅力”号火星漫游车已经搭载了自主漫游技术，可以每年运动10～20 km，期间采集超过20个岩石样本[1]；而以往的火星车，只能每年运动1～4 km的距离，只能执行较为简单的任务[2].因此，火星漫游车利用搭载的传感器，实现自主漫游，可以极大提高火星漫游车在星表执行复杂任务的能力[1].

地外巡视器在火星表面的自主漫游，需要解决2大核心问题：对机器人自身的实时位姿估计和对周围地形的有效建模.其中，对自身状态的估计可以使用板载传感器实现位姿估计，对地形的感知可以在机器人运动过程中实时构建地图来实现.

基于视觉的SLAM系统通过固定在机器人上的相机，实现对机器人自身的位姿估计并对周围环境的地图构建[3-5].根据相机数量的不同，可以将视觉SLAM系统分为单目SLAM、双目SLAM和多目SLAM；此外，还可以将视觉观测与其他传感器融合，实现更加精确鲁棒的SLAM系统[4]，例如将视觉与惯性测量单元IMU(inertial measurement unit)相融合的视觉-惯性SLAM系统.

利用视觉观测估计自身位姿的基本假设是周围环境保持静止，视觉特征在图像上的移动完全由机器人自身运动引起，进而通过观测图像特征的运动，计算机器人相对于周围环境的运动，实现位姿估计.

能够实时、精确地感知复杂地形是地外巡视器进行自主漫游的基础[6]，这就需要在机器人运动过程中实时建立周围环境的地形图.地图表示可以分为稠密地图和稀疏地图.其中，稀疏地图多用于辅助定位，稠密地图则多用于导航规划.在地外探测任务中，巡视器需要通过对复杂地形的感知，为上层路径规划、避障等高层次算法提供依据，因此多采用稠密的地图表示.考虑到巡视器的资源约束[7]，本文利用双目稠密点云建立2.5维的高程图[8-9]来应对外星探测任务中计算资源受限、非结构化地形等挑战[9-10].

然而，外星环境中的亮度变化、非结构化纹理特征等因素的影响，会导致过曝、视觉退化等问题；另一方面，仅用视觉传感器难以精确恢复尺度信息，将双目恢复的误差引入对自身位姿的估计中，造成运动距离的误判.IMU可以测量加速度、转动速度，是一种直接感知自身运动的传感器.将视觉对环境的观测与IMU的自身运动感知相结合，可以减少感知系统对外部环境的依赖，实现高精度的尺度恢复，有效提高感知系统的鲁棒性[11].

本文针对火星上非结构化场景对机器人自主导航提出的挑战，提出了一种基于双目视觉与IMU融合的轻量化感知系统，解决了火星车的自主定位与建图问题；设计了基于多状态约束卡尔曼滤波算法的位姿估计模块与高程地图构建模块的概率最优融合方法，保证了整个系统的概率一致性；应用GPU加速技术，设计并实现了基于GPU的并行建图算法，最终在低功耗的板载系统上实现了稠密高程地图的实时构建；在自行搭建的移动平台上模拟资源受限的场景并充分测试了所提算法的鲁棒性和精度.

后文首先介绍整个系统的构成，再分别详细介绍系统中各个模块.后续小节分别为：1)首先介绍本文采用的符号含义；2)介绍整个系统框架和主要模块；3)详细介绍位姿估计模块；4)详细介绍地图构建模块；5)实验结果；6)总结与展望.

1 符号说明

1.1 坐标系

在本文中，FX表示X坐标系.表1为本文用到的坐标系及其符号.

表1 坐标系符号及含义Tab.1 Coordinate system symbols and meaning

T(t):R→SO(3)×R3

(1)

t→{R,p}

(2)

1.2 李代数符号

旋转矩阵R∈SO(3)对应的李代数记为ω∈SO(3)，其中SO(3)表示SO(3)对应的李代数集合.因此，存在互为逆运算的等式

R=Exp(ω)=exp(ω∧)

(3)

ω=Log(R)=ln(R)∨

(4)

其中：ω∧表示向量ω对应的反对称矩阵；对于旋转矩阵R，ln(R)是一个反对称矩阵，ln(R)∨则是其对应的三维向量；角标∧和∨代表的运算互为逆运算；exp()和ln()分别表示矩阵指数运算和矩阵对数运算.

1.3 状态表示

2 系统描述

在前人工作的基础上，本文提出了基于视觉-惯性的感知系统，能够在计算资源受限的条件下，实现局部高程地图的构建和对自身位姿的实时估计.整个系统的结构框图如图1所示.

图1 系统架构示意图Fig.1 System architecture diagram

系统输入包括传感器输入和当前位姿、当前地图.传感器输入包括双目图像和IMU测量得到的加速度、角速度，双目图像和IMU使用统一的外部时钟以不同频率进行触发.系统输出包括机器人当前时刻相对于初始时刻的位姿、以及以机器人为中心的局部高程地图.其中，以机器人在初始时刻的本体坐标系为世界坐标系，在任意时刻，机器人的位姿为当前时刻的本体坐标系在世界坐标系下的表示.局部高程地图可以提供以机器人本体坐标系为中心，周围一定区域的网格高度和置信度.

对于位姿估计模块，为充分降低计算复杂度，本文采用基于多状态约束卡尔曼滤波的融合算法，使用IMU测量得到的惯性信息计算先验位姿，再使用图像观测对位姿进行更新，得到最终的位姿估计.其中，视觉观测模型采用基于特征点的观测模型，将特征点的重投影误差作为观测残差，实现对位姿的更新.

对于地图构建模块，本文采用基于双目点云的局部高程地图构建算法，估计机器人周围局部栅格地图的高度和置信度.首先将矫正后的双目图像恢复深度，得到双目稠密点云；再分别使用位姿估计模块的输出和稠密点云更新当前地图，最后使用卡尔曼滤波算法将2张更新后的地图进行融合，得到最终的局部高程地图.在机器人不断运动的过程中，局部地图不再更新的部分会保存到全局地图当中，用于后续全局的导航规划.

3 位姿估计模块

本节详细描述系统中的视觉-惯性位姿估计模块，本模块使用多状态约束卡尔曼滤波(MSCKF)算法进行多传感器信息融合.后续会分状态定义、IMU预测模型和相机观测模型3个部分进行阐述.

3.1 状态向量定义

在tk时刻位姿估计模块的状态向量xk的定义如下：

(5)

其中：xI,k表示tk时刻的IMU状态向量；xcl,k为tk时刻保存的历史状态窗口，具体形式为

(6)

(7)

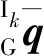
3.2 预测模型

MSCKF算法的预测部分基于IMU观测的连续时间动力学模型

(8)

6轴IMU包括3轴陀螺仪和3轴加速度计，分别测量转速和线加速度，且测量值表示在FI坐标系下.在tk时刻IMU的测量值可以表示为

(9)

其中，Gg为重力加速度在世界坐标系FG中的表示，ng(tk)和na(tk)为零均值高斯白噪声.

假设相邻2帧图像分别在tk和tk+1时刻收到，则需要使用[tk,tk+1]时间区间内的IMU测量值进行数值积分获得这段时间机器人的位姿变化量，进而获得tk+1时刻的机器人先验位姿

(10)

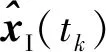
为将预测模型得到的先验状态向量与视觉观测相结合，还需要计算先验状态向量的协方差矩阵.因此，在进行状态预测的同时，还需要融合上一时刻的协方差矩阵与IMU测量噪声，为此定义误差状态向量

(11)

(12)

(13)

其中求解上式的初值条件为：Φ(tk,tk)=I15+6M.使用数值计算或解析求解Φ(tk+1,tk)，就可以使用标准的扩展卡尔曼滤波(EKF)框架计算先验位姿的协方差矩阵

Pk+1|k=Φ(tk+1,tk)Pk|kΦT(tk+1,tk)+Qd,k

(14)

其中Qd,k为离散时间系统的噪声协方差矩阵

(15)

MSCKF会在每次状态预测后，将当前的状态中的位姿分量克隆下来，保存在历史位姿窗口xcl中，用于后续观测更新.

3.3 视觉观测模型

本文使用基于特征点的视觉观测，首先对图像进行特征提取并在多帧之间进行特征匹配，被多帧图像观测到的特征点会被三角化，最后三角化后的特征点重投影到图像平面上，与每一帧的实际观测结果之间的误差即为观测残差.

MSCKF算法会在tk时刻将过去M个图像观测对应的位姿保存在状态向量xcl,k中，同时将特征点保存下来.假设tj(j=k,k-1,…,k-M+1)时刻相机观测到了坐标为Cjpf=[xjyjzj]T，该坐标点在的三维坐标与其在图像平面上的二维像素坐标(假设相机已经事先标定过内外参，此处指的是正则化后的相机观测)之间的关系，可以用投影模型描述：

(16)

(17)

(18)

其中Hx,j和Hf,j是观测模型关于状态向量先验值和特征点位置估计值的雅可比矩阵.由于历史窗口中存在多个状态观测到这个特征点，因此会有多个上述方程，将其统一整理成矩阵形式可以得到

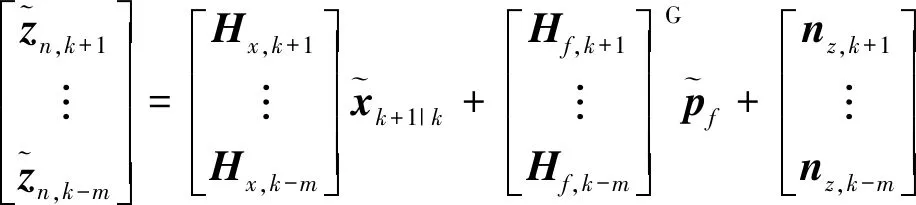
(19)

其中最后一步使用了左零空间映射，将方程两边同时乘以Hf矩阵的左零空间，从而在充分利用视觉观测的同时，避免在状态向量中加入特征点位置.整理成最终形式，即可使用标准的EKF更新算法对状态进行更新.

4 地图构建模块

本节详细介绍地图构建模块，本文采用的是以机器人为中心的网格区域2.5维高程图，用于对机器人周围的地形结构进行建模.

4.1 状态定义

地图构建模块首先将机器人周围的区域划分为相同大小网格，网格大小和数量由外部参数给定；然后计算每个网格的高度期望值与估计方差.因此，针对局部地图中的每个栅格，都定义相应的状态向量为

Vi=[MxiMyihi]T

(20)

其中(Mxi,Myi)为该栅格中心在地图坐标系下的坐标.每个栅格都用来描述一块地形的高度，不会随着机器人的运动而改变，而地图坐标系会随着机器人的运动而运动，因此(Mxi,Myi)也需要随着机器人的运动而实时更新.

4.2 使用点云更新地图

本文使用矫正后的双目图像恢复深度，得到稠密点云.然而，由于双目相机计算得到的三维点集数量非常多(大约几万个点)，且相当一部分三维点与机器人位置相聚很远，从而增加了无谓的计算量.因此本文使用体素滤波算法对稠密点云进行过滤采样，得到并截取机与机器人距离适中的点云子集，作为最终用于建图的点云观测.

(21)

(22)

(23)

进而可以使用雅可比矩阵计算高度估计值的不确定度

(24)

其中:ΣC为传感器的观测噪声；根据本文对FM坐标系的定义，FM必须始终与FG保持z轴对齐，因此相机绕x轴和y轴的姿态不确定度Σθ会被引入局部地图中.需要注意的是，FM与FI(以及FC)的相对位移和偏航夹角都是保持不变的，所以在计算局部地图方差的时候不需要考虑平移的不确定度，这里的Σθ也不包含偏航角的估计方差.

(25)

(26)

4.3 使用位姿更新地图

从前述可知，地图坐标系FM与本体坐标系FI(以及相机坐标系FC)之间的相对位置和绕z轴的相对转角保持不变，FM会随着机器人的运动而发生位置和偏转角的变化.然而，地形却是与全局坐标系保持静止的，因此地图中的每一个栅格也应该随着机器人的运动而更新.

当机器人运动时，地图中的所有栅格可以分为2类：存在对该栅格高度的最新观测和该栅格内没有最新观测.对于第一种情况，地图的更新由落入该网格内的观测引起，本文重置该栅格状态的方差为

(27)

(28)

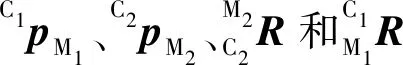
由上式机器人运动前后对同一个特征点的观测关系，可以得到运动后的观测方差为

(29)

其中，ΣV,1和ΣV,2分别表示运动前后的地图状态估计协方差矩阵，Σp和Σθ分别为机器人状态估计的位置协方差矩阵和姿态协方差矩阵.JV、Jp和Jθ分别为公式对地图状态、机器人位置和机器人姿态的雅可比矩阵，表达式为

(30)

(31)

(32)

从而完成机器人位姿对地图的更新.

4.4 地图融合

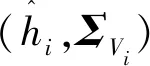
本文使用式(33)和(34)计算hi,min和hi,mean

(33)

(34)

对于栅格i的平均值hi,mean，本文从栅格i相邻的所有栅格中查找高度估计值在[hi,min,hi,max]区间内的栅格，将它们的高度取均值得到hi,mean.

4.5 全局地图构建

全局地图构建的目的是为全局导航规划.为更有序地管理地图，我们采用之前工作中子地图的概念[7].在机器人移动过程中，不断将局部地图中不再更新的部分存到当前活跃的子地图中如图2中的子地图3，在行进一定距离后，该子地图会存成一个不活跃的子地图如图2中的子地图1、2，在极端计算约束下，不活跃的子地图可以文件形式存储在硬盘当中，以减少对内存的需求.由于该建图机制只处理不再更新的部分，因此在计算上具有轻量快速的特性.

图2 全局地图构建示意图Fig.2 Global map construction diagram

4.6 GPU加速

在4.2小节中，要使用点云中的每个观测计算所在栅格的高度，而本文使用的双目稠密点云规模可能达到数万个，即使截取近距离点云子集、提速滤波降采样等方法大幅度减少点云数量后，仍然有数千个点.要在收到每帧图像后，都使用几千个点更新地图，在计算资源受限、CPU要承担其他多种任务的情况下，无法满足实时性需求.此外，每次机器人移动，都要对局部地图的每个栅格进行更新，且每个栅格的更新相互独立，可以并行运算；输出地图之前，需要对每个栅格进行融合，此步骤同样可以并行加速[8].

NVIDIA公司推出过一系列具有板载GPU的低功耗开发板，例如TX2、NX和AGX Xavier等.因此，配备GPU的低功耗板载系统已经相对成熟，是未来航空航天领域值得尝试的方案.本文使用GPU对点云更新地图、位姿更新地图和地图融合3个部分进行加速，可以在上述开发板上实现4 Hz以上的地图构建频率.

5 实验结果

实验使用的测试平台如图3所示，测试使用4轮移动平台，并搭载了多种传感器和工控机，用于数据采集.

本实验用到的传感器包括双目相机(图3中标注1的红色方框)和一个IMU(图3中标注2的黄色方框).相机型号为FLIR BFS-PGE-04S2M工业相机，IMU使用XSENS MTI-300系列.其中IMU的测量频率为400 Hz，实验中只使用了IMU测量的角速度和线加速度；双目图像分辨率均为640×480，相机频率为16 Hz.

图3 实验平台与装备的传感器Fig.3 Experimental platform with sensors on it

数据采集过程中，IMU和双目相机使用自研同步电路板实现传感器的外触发同步，保证了IMU和双目图像的采集是时间对齐的.数据采集使用一台配有Ubuntu18.04操作系统的工控机完成，工控机CPU为Intel i7处理器，内存空间为16 G.

5.1 位姿估计实验结果

如图4(a)所示，实验测试场景为浙江大学玉泉校区内第18教学楼前的一处草坪.对位姿估计模块的测试与评估的方式如下：首先标记移动平台初始位置和姿态，随后控制4轮移动平台绕草坪运动一周，最后使其回到原地，则此时的位姿估计结果相对初始时刻的位姿即为算法的位姿估计的绝对误差.位姿估计算法实现基于Open-VINS[12]开源算法框架.

需要注意的是，图4(a)中的路径只是示意图，并不是机器人实际运行的路径，其中机器人起始位置在图4(a)中使用星号进行标记.此外，在测试过程中，移动平台以非常低的运动速度和加速度运动，以尽可能地模拟地外巡视器的运动.

实验结果如图4(b)所示，最终位姿估计的绝对误差为1.93 m，总运动距离129.59 m，相对误差为1.49%.位姿估计的误差相比于已经开源的视觉-惯性导航系统VINS(visual inertial navigation system)稍高的原因在于：1)为模拟地外巡视器的运动，实验中移动平台的速度和加速度都有严格限制，缺乏足够的运动激励，这给IMU的初始化提出较大的挑战，导致IMU在后续运行过程中受到重力的干扰而降低精度；2)为控制计算复杂度，降低计算资源占用率，本文采用的方法不包含已有SLAM系统中的因子图优化，同时要保持路标点的稀疏性(实验中只在状态向量中维护了50个路标点的位置).

图4 定位模块测试结果Fig.4 Results of self-localization

为体现本文方法与现有方法的优越性，本文与视觉惯性融合定位的代表性作品，VINS-Fusion进行对比，绘制其位姿估计的轨迹并计算终点误差.VINS-Fusion的计算结果如图4(c)所示.可以看出，VINS-Fusion估计出的轨迹明显与实际运动轨迹不符合，且最终绝对误差为3.41 m，相对误差为2.63%左右，要显著高于采用的MSCKF方法.这可能是因为VINS-Fusion是基于优化的方法，对相机和IMU之间外参的标定精度更加敏感，以及机器人平台慢速运动会导致IMU测量值的信噪比降低所致.

为进一步为路标点数和里程估计精度之间建立定量联系，调节路标点的数量，并衡量对应的里程估计精度，结果如表2所示.

表2 不同路标点对应的里程估计精度Tab.2 Accuracy of odometry with different number of landmarks

其中相对误差用绝对误差除以总距离得到的百分比表示.

从表2中可以看出，当路标点从100个逐渐减少到0个的过程中，里程估计的相对误差也在逐渐增大.注意，虽然75个路标点和50个路标点得到的相对误差在保留2位小数的情况下是相同的，更高位的数值上75个路标点的误差要略小.此外，当路标点数量为100个、75个和50个时，里程估计的相对误差近提高了0.06%，而路标点数量进一步减小，相对误差迅速增大.该实验结果表明，对于实验采用的场景而言，50个路标点已经充分发挥了视觉观测对里程估计的更新作用，再进一步增加路标点数量无法显著提高历程估计的精度.而使用更小的路标点则会导致视觉观测的信息无法被充分利用，显著降低里程估计精度.

对于路标点数量的增加对计算资源消耗的影响，可以通过计算复杂度进行分析.由于路标点会被加入到状态向量中进行联合估计，重复观测到该路标点时需要对其位置进行更新，路标点位置更新融合的矩阵运算是计算资源消耗的主要来源.状态向量规模的增大，会导致矩阵规模以平方速度增加，而状态更新过程中的矩阵求逆运算，复杂度为O(n3)，其中n为状态向量的规模.因此，本文所述方法的计算复杂度与状态向量的维度n之间的关系为O(n3).

5.2 地图构建实验结果

地图构建模块的算法实现基于以前的工作[7-8]，核心代码在GPU上运行，最终实现了实时地图构建.需要注意的是，文献[7]和文献[8]中提出的算法均使用激光雷达采集的点云进行验证，本文仅使用双目相机，使用双目深度恢复算法[13]生成三维点云.点云恢复的效果如图5所示，图5(a)为双目相机采集的图像，其中左上角标注CAM:0的图片为左目相机采集的图像，标注CAM:1的图片为右目相机采集的图像，图5(b)为使用双目图像恢复的三维点云.可以看出，使用双目图像恢复出的点云数据足够稠密，可以用于感知移动平台前方的障碍物，并用于构建地形图.本文采用文献[11]提出的双目深度恢复算法，避免了对三维点云的优化过程，实现了三维稠密点云的实时生成.

图5 双目重建点云的效果图Fig.5 Pointcloud generated from stereo images

在测试地图构建模块的实验中，首先将双目图像与IMU相融合，得到移动平台的位姿；与此同时，将矫正后的双目图像输入双目深度恢复的算法模块，生成三维稠密点云.最后，将位姿估计模块输出的当前位姿，连同三维稠密点云一起输入到地图构建模块，用以构建局部地图.

图6(a)为最终构建的全局地形图，图中蓝色为地图中相对较高的区域，绿色为相对较低的区域，黄色区域的高度介于2者之间；全局地形图中右下角部分是移动平台周围的局部地图.从整体俯视图可以看出，构建的地形图较为稠密，可以感知环境中较小的障碍物.地图的局部细节可以从图6(b)和图6(c)体现，可以看出，地图呈现中间平坦，两侧突起的形状，这与中间路面、两侧为障碍物的实际环境相符，可以为机器人躲避障碍物，并进行全局路径规划提供可靠依据.

图6 使用点云构建的高程地图Fig.6 Elevation map constructed with pointcloud

5.3 系统运行效率与资源占用

将位姿估计模块和地图构建模块同时在一块30W的NVIDIA AGX Xavier板载系统上运行，使用开发板自带的资源监测命令tegrastats查看CPU、RAM内存和GPU3项主要资源的占用率.分别记录本文所提的感知系统运行前后的资源占用，其中八核CPU运行前后的占用率如表3所示.

表3 感知系统运行前后的CPU占用率Tab.3 CPU usage before and after the operation of perception system

运行前后RAM内存占用率分别为2 762 MB和5 410 MB；对应的GPU占用率分别为1%和69%.虽然算法运行过程中，计算资源占用率处于波动状态，但是上述实验数据可以大体反映算法的资源占用情况：CPU占用约35%，RAM内存占用约2.6 GB，GPU占用约65%.

在感知系统运行的同时，分别查看位姿估计模块和地图构建模块的输出频率，如表4所示.

表4 感知系统输出频率Tab.4 Output frequencies of the perception system

从表4可以看出，位姿输出频率与IMU的数据采集频率相同，这是因为每次获得IMU测量数据后，可以在上一时刻位姿的基础上，使用IMU观测动力学模型对系统位姿进行预测.而位姿的图像更新频率仍为16 Hz，与图像采集频率相同.若使用NVIDIA开发板的CPU进行地图构建，可能要花费数十秒的时间才能完成一帧点云数据处理.得益于本文采用的GPU加速算法，地图构建模块的输出频率可以达到4 Hz，足以满足地外巡视器完成路径规划、避障等任务的实时性需求，同时极大降低整个系统的CPU占用率.

为进一步证明使用GPU加速地图构建模块的必要性，记录了运行全程的地图构建输出频率.与之对比，使用相同的实验数据，运行了不适用GPU加速的高程地图构建算法，并记录了其局部地图输出频率.有无GPU加速的地图输出频率如图7所示.从图7可以看出，使用GPU进行加速时，地图构建的输出频率可以稳定在大约4.3 Hz，而使用CPU构建地图的算法只能以大约0.2 Hz的频率输出局部地图.从而证明本文所提的GPU加速方法的必要性和先进性.

图7 有无GPU加速的高程地图输出频率对比Fig.7 Output frequencies of elevation maps with or without GPU acceleration

6 总结与展望

本文针对巡视器在火星表面的自主导航任务，提出一套轻量高效的感知系统，该系统融合双目视觉与IMU的测量信息，可以实时估计机器人的位姿，并使用双目图像恢复的稠密三维点云，构建局部地图与全局地图，以满足巡视器障碍物检测与全局路径规划等任务的需求.在此基础上，本文进一步使用GPU对地图构建模块的部分进行加速，将地图构建频率提高到4 Hz以上，实现了地图的实时构建，进一步帮助巡视器在火星表面运行过程中能够快速检测到障碍物.

本文通过设计实物实验，充分验证了所提感知系统的有效性、精度和运算效率.实验表明，本文所提出的感知系统，能够在30 W的板载系统上实时运行，输出探测器位姿和环境地形图，且计算资源仍有剩余.

从实验中可以看出，在运动速度、加速度都比较低的移动平台上，IMU初始化存在激励不足、重力方向判定不准的问题，会降低系统位姿估计的精度.如何解决IMU在运动速度缓慢的平台上的这一问题，是后续研究的重点.