论多元积分学中的降维思想

田卫章

(商丘职业技术学院，河南 商丘 476100)

多元函数的积分运算在数学分析学习中占有重要地位.在积分运算中，我们曾研究过牛顿-莱布尼茨公式、格林公式、高斯公式、斯托克斯公式等积分运算的方法，这些积分运算方法的共同特点是将积分区域进行不同形式的“降维”，从而使多元积分计算问题得到简化.

1 牛顿-莱布尼茨公式中的降维思想

1.1 定积分的牛顿-莱布尼茨公式及其所体现的降维思想

微积分第二基本定理，即牛顿-莱布尼茨公式把微分与积分从概念与计算上同时联系起来，这是使微积分理论形成一个体系的一个重要标志，其具体内容如下：

1.2 牛顿-莱布尼茨公式的二重积分形式及其降维思想

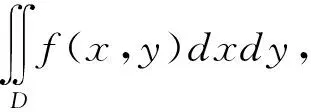
1.3 牛顿-莱布尼茨公式的曲线积分形式及其降维思想

注牛顿-莱布尼茨的曲线积分形式是将二元函数在平面曲线C上的积分值转化为函数在平面曲线C的两端点的函数值之差，从而将积分区域由1维降至0维[4].

1.4 牛顿-莱布尼茨公式的降维应用

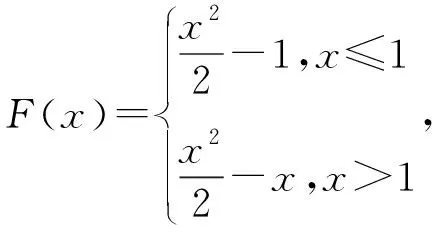
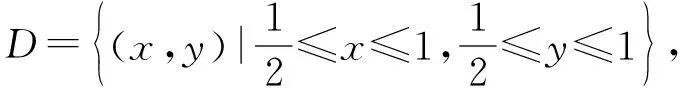
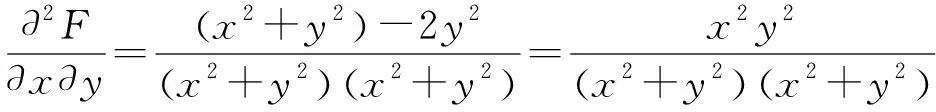
2 格林公式中的降维思想

2.1 格林公式定义及其降维思想

格林公式是牛顿-莱布尼茨公式在多元函数积分学中的推广，在多元函数积分学中占有非常重要的地位.格林公式给出了平面区域D上的二重积分与沿这个区域的边界L的曲线积分之间的联系，其具体内容如下：

注格林公式的表达简单明了，是牛顿-莱布尼茨公式在多元积分学中的推广，可简化二重积分.格林公式揭示了平面区域上的二重积分与沿这个区域的边界曲线上的曲线积分之间的联系，可把函数的平面积分转化为平面曲线的积分.格林公式是将面积分转化为线积分的工具之一，可将函数的积分区域由2维降至1维.

2.2 格林公式的降维应用

格林公式计算平面面积是其降维思想的基本应用之一，一般形式下常见面积计算公式有以下3种[6].

例3计算抛物线(x+y)2=ax,(a>0)与X轴所围的面积.

解方法一：

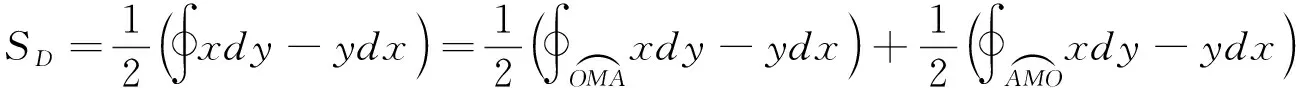
方法二：

例4计算由星形线x=a(cosθ)2,y=b(sinθ)2(0≤θ≤2π)所围成的平面图形的面积.

解设L为星形线x=a(cosθ)2,y=b(sinθ)2(0≤θ≤2π)的边界，选取正方向，D是由L所围成的闭区域，其面积为A,则由格林公式可得

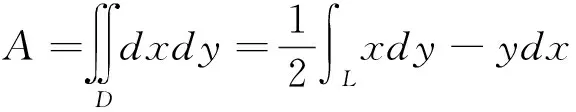
注从以上2个应用格林公式计算平面区域面积的例题中可以看出，格林公式揭示了平面区域上的二重积分与沿这个区域的边界曲线上曲线积分之间的联系，从而将积分区域由2维降至1维，可大大降低曲线积分的计算难度.

3 斯托克斯公式中的降维思想

利用两类曲线积分间的联系和两类曲面积分间的联系，可得斯托克斯公式的另外三种形式：

其中n1=(cosα,cosβ,cosγ)为分片光滑的有向曲面S在点(x,y,z)处的单位法向量.

其中n2=(cosθ，cosφ，cosω)为分段光滑的有向曲线L在点(x,y,z)处的单位切向量.

注斯托克斯公式是微积分基本公式在曲面积分情形下的推广，也是格林公式的推广.斯托克斯公式表明：分片光滑的空间曲面S上的曲面积分可转化为该空间曲面S的分段光滑的边界曲线L上的曲线积分.也就是说，斯托克斯公式揭示了函数在分片光滑的曲面上的曲面积分和函数在该曲面的分段光滑的边界曲线上的曲线积分之间的联系，可将函数在空间曲面上的积分转化为空间曲线积分，从而将积分区域由2维降至1维[8].

4 高斯公式中的降维思想

4.1 高斯公式的定义及其降维思想

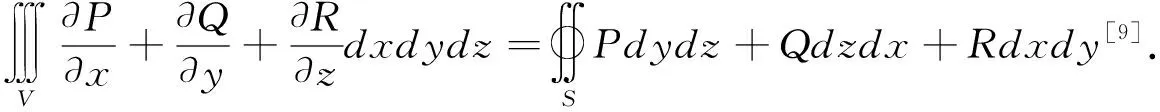
注高斯公式揭示了空间区域的三重积分与其边界曲面上的曲面积分之间的关系，其可将函数的空间体积分转化为空间曲面积分，从而将积分区域由3维降至2维.

4.2 高斯公式的降维应用

利用高斯公式的降维思想可计算三重积分，特殊情况下，可利用高斯公式的降维思想求得物体的体积.具体求体积的方法可利用如下公式:

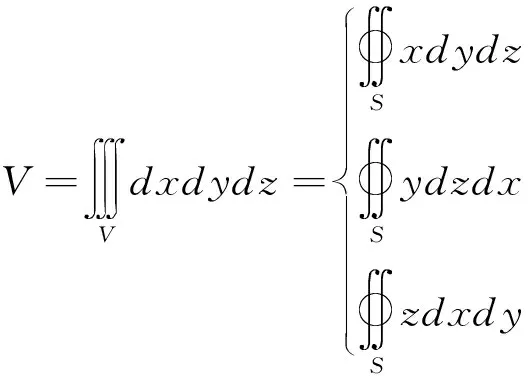
下面通过例5，例6进一步说明.

解设椭球面的参数方程为x=asinφcosθ,y=bsinφsinθ,z=ccosφ,(0≤θ≤2π,0≤φ≤π), 则

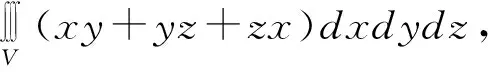
解令P=x2y,Q=y2z,R=z2x，则

5 一般积分形式计算中的降维思想

重积分的计算过程实质上是把积分区域进行降维的过程，计算定积分、重积分、曲线积分、曲面积分的基本思想是一致的，都是将高维次的积分区域形式转化为较低维次的积分区域形式计算，下面逐一进行说明.

5.1 二重积分中的降维思想(化二重积分为二次积分)

5.1.1 二重积分在直角坐标系中的降维

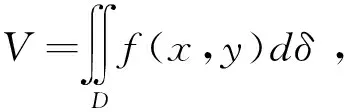
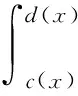
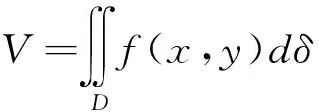
从以上讨论可以知道，二重积分的计算就是以含参量积分为中介，化二重积分为两次定积分，实现积分区域由2维降至1维，两次利用牛顿-莱布尼茨公式得出最后结果.

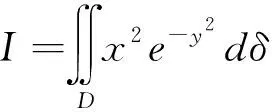
5.1.2 利用极坐标将二重积分降维

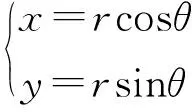
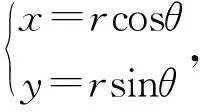
5.2 三重积分中的降维思想

三重积分通常可利用直角坐标、柱面坐标和球面坐标进行计算.坐标的选择取决于积分区域和被积函数的特征，具体计算则通过固定变量降低被积函数的元数，同时利用投影法降低积分区域的维数.三重积分有“先二后一”“先一后二”和“三次积分法”，即“3=2+1”“3=1+2”和“3=1+1+1”.

5.2.1 三重积分在直角坐标系下转化为累次积分的降维思想

注定理7表明三重积分可先选取其中一元变量，再用垂直于此变量的切面去截积分体，所得截面方程即为二重积分区域中的D，最后确定最初选取变量的范围.这样，就把三重积分转化为先一次积分后二次积分，实现积分区域的降维，此方法又称“穿针法”.

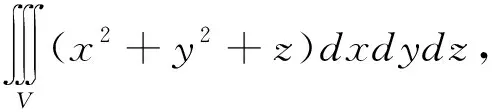
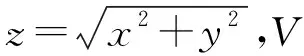
注定理8表明计算三重积分时，可先固定一自变量z的范围，然后用垂直于此自变量所在坐标轴的切平面去截取积分区域，所得截面方程即为积分区域中的Dz，这样就把三重积分转化为先二次积分再一次积分，实现积分区域的降维，此方法又称“切片法”.

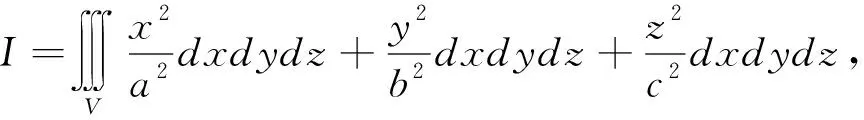
注三重积分计算过程的大致思想是：将三重积分化为累次积分，而化为累次积分的方式可以有所不同，从而将积分区域实现不同形式的降维.直角坐标系下的三重积分转化为逐次积分的方法可总结如下：

若f(x,y,z)在V={(x,y,z)|a≤x≤b,c(x)≤y≤d(x),e(x,y)≤z≤g(x,y)}上连续，记R={(y,z)|c(x)≤y≤d(x),e(x,y)≤z≤g(x,y)}，则

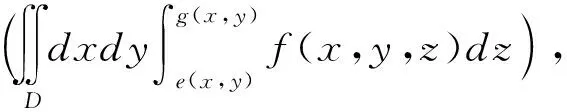
5.2.2 利用柱面坐标变换将二重积分进行降维

注柱面坐标变换可将三重积分的计算过程简化，将三重积分转化为先一次积分后二重积分的累次积分，从某种意义上说，也是积分区域的降维过程.

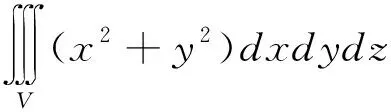
5.2.3 利用球坐标变换将三重积分进行降维

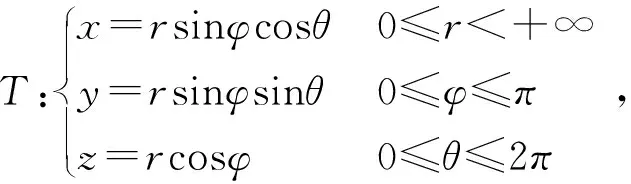
在球坐标系下，当区域V′为集合V′={(r,φ,θ)|r1(φ,θ)≤r≤r2(φ,θ),φ1(θ)≤φ≤φ2(θ),θ1≤θ≤θ2}时，

注球坐标变换可将三重积分的计算过程适当简化，通过球坐标变换，可将三重积分转化为三个单次积分，从某种意义上说，将3维积分区域转化为1维积分区域，是积分区域的降维过程.

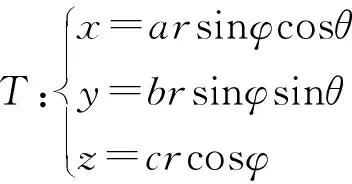
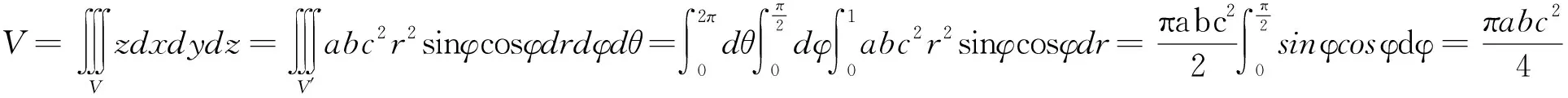
6 结语

多元积分中的几个重要公式及一般形式的积分计算都体现了通过降低积分区域维数进行求解的思想.本文只是从一些具体公式及具体计算方法上简要地论述了多元积分学中的降维思想.了解有关积分学中的降维思想，可以转换我们思考问题的角度，使问题中的关系在新的维系中更加直观、简约，不仅深化我们对积分学的进一步认识，也可提高我们的数学综合素养.