基于贝叶斯神经网络的机床热误差建模*

王子涵 杨秀芝 段现银 蒋宇辉 王兴东

(①武汉科技大学机械学院，湖北 武汉430070；② 湖北理工学院智能输送技术与装备湖北省重点实验室，湖北 黄石 435003)

随着精密制造技术的广泛应用和快速发展，现在市场对数控机床加工精度的需求日益增长。由于在加工操作期间由诸如电动机和轴承之类的部件产生的热量，机床的温度升高使机床形变引起热误差，并且整体精度降低。更为重要的是大量科学研究和加工实践表明，热致误差约占高精度机床总误差的40%～70%[1-2]。目前减少机床的热误差的方法主要有2个方向，分别是硬件和软件。硬件方向是从机床本身的材料和结构进行研究，通过采用新型材料和改善结构来从根本上减少机床热误差。软件方向是利用补偿的思想建立准确的机床热误差预测模型，通过该模型预测补偿误差去抵消机床的原始热误差，从而达到减少热误差的目的。而因为软件研究的经济成本比硬件少得多，且适应性更强，因此软件补偿是数控机床热误差研究的最重要方向。

如余文利等[3]使用混沌粒子群优化的灰色模型(GM)来建立热误差模型，提高了模型的迭代速度，而比单一的GM模型和ANN的预测精度更高；张毅[4-6]提出了结合灰色模型和反向传播(BP)神经网络的灰色神经网络，通过对神经网络结构的优化，提高了模型的泛化能力；郑金勇等[6-7]利用遗传算法(GA)来优化灰色神经网络从而建立热误差模型，与BP神经网络相比进一步提高了模型的预测精度。李彬等[8]基于GA进一步优化基于小波分析优化过的BP神经网络，用小波基函数替代隐含层节点的激励函数，解决了BP神经网络易于陷入局部最小值过度拟合的问题。

而本文使用了一种新的高效的基于BP神经网络的算法，通过学习神经网络权重上的概率分布，使模型在拟合不足和拟合过度之间达到平衡，称为贝叶斯神经网络(BNN)[9-13]。BNN在训练样本数据稀少时有着比其他网络更好的性能，适合机床热误差实验数据少，难获取的特性[14]。

1 贝叶斯神经网络模型

1.1 贝叶斯神经网络原理

贝叶斯神经网络，是一种为通过为神经网络的权重引入不确定性进行正则化的新型神经网络模型，使之可以任意精度近似任何连续函数。

如图1中所示的网络体系结构是最常用的一种标准BP神经网络，由输入层、隐藏层和输出层组成。隐藏层通常使用S型激活函数，而输出层通常使用线性函数。一个神经网络模型可以视为一个条件分布模型P(y∣x,w)，输入x，输出预测值y的分布，w为神经网络中的权重[9]，每个权重都有一个固定值，这是由经典BP神经网络提供的。相应地，神经网络的学习可以视作是一个最大似然估计(MLE)：

(1)

其中：D对应我们用来训练的数据集，xi为每个节点的输入，yi为每个节点的输出，w为每个节点的权重。MLE 中不对w的先验概率作假设，也就是认为w取什么值的机会都均等。如果为w引入先验，那就变成了最大后验估计(MAP)：

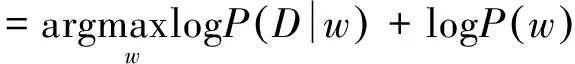
(2)

贝叶斯估计同样引入先验假设，与 MAP 的区别是贝叶斯估计求出w的后验分布P(w∣D)，而不限于argmax值。如图2所示，神经网络的权重为一个分布而不是一个具体的数值，这样我们就可以为神经网络的预测引入不确定性。由于我们求得的是分布，基于w由x预测y的概率模型为：

(3)

此时预测值y为后验分布P(w∣D)上的所有可能的神经网络预测值的期望。根据贝叶斯理论，后验分布为：

(4)

P(D)取决于样本数据集，而对于P(w)的形式，文献[10]给出了一个混合尺度高斯先验:

(5)

其每个权重其分布的先验都是2种相同均值、不同标准差的高斯分布的叠加。

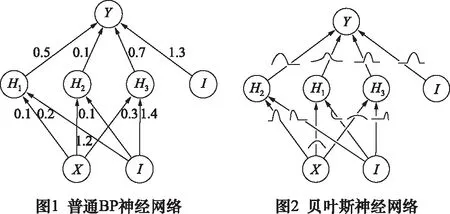
1.2 贝叶斯正则化

为了后验分布P(D∣w)和期望，Blundell C等[10]利用变分的方法让高斯分布θ的参数代入q(w∣θ)去逼近真正的后验，把求后验分布的问题转变成求解最好的θ问题，这个过程可以通过最小化2个分布的 KL 散度实现：

Eq(w∣θ)[logP(D∣w)]

(6)

Blundell C[10]把第一项叫作复杂性代价，描述的是权重和先验的契合程度；把第二项叫作似然代价，描述对样本的拟合程度。我们可写成目标函数的形式：

F(D,θ)=DKL[q(w∣θ)‖P(w)]-

Eq(w∣θ)[logP(D∣w)]

(7)

优化这个目标函数就是贝叶斯神经网络正则化，在2种代价中取平衡。

2 实验

在机床工作期间，由于进给机构丝杠和螺母之间的摩擦以及轴承的摩擦而产生大量的热量，这导致机床结构的变形影响精度。因此，除了主轴系统外，有必要测量驱动系统的热特性，其工作主要包括温度场和热误差2个方面，得出温度和误差之间明确的数学关系。本文的实验平台为某公司的BF-850L立式五轴数控机床，本文的研究主轴误差为Z轴误差，平台的搭建如图3a所示，测量热误差仪器为雷尼绍RENISHAW激光干涉仪和菲力尔红外热像仪FLIR TG42；温度的测量分为2种方式，第一种是接触式测量，例如主轴电机和丝杆螺母通常使用磁吸式温度传感器进行测量；而对于难以测量的部件，我们使用红外热像仪辅助测量数据。在本文中，我们使用了红外热像仪测量主轴轴承T2的温度数据。

在实验正式开始之前，先测量了机床在环境温度T0下的Z轴方向主轴误差E几何，即几何误差，研究[15-16]表明机床误差主要由几何误差和热误差构成。故

E热=E总-E几何

(8)

如此，根据正式实验中激光干涉仪测量数据E总就很容易得出主轴热误差E热。

在热误差实验中，温度传感器的具体位置温度测点为表1和图3b所示。为了模拟正常工作的工况，主轴的转速被设定为8 000 r/min，X、Y、Z进给轴以20 m/min做往复运动，每15 min测量1次主轴的重复定位精度和各温度点当前温度数值。

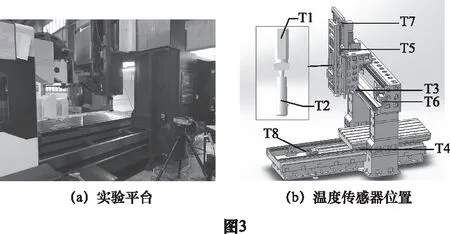
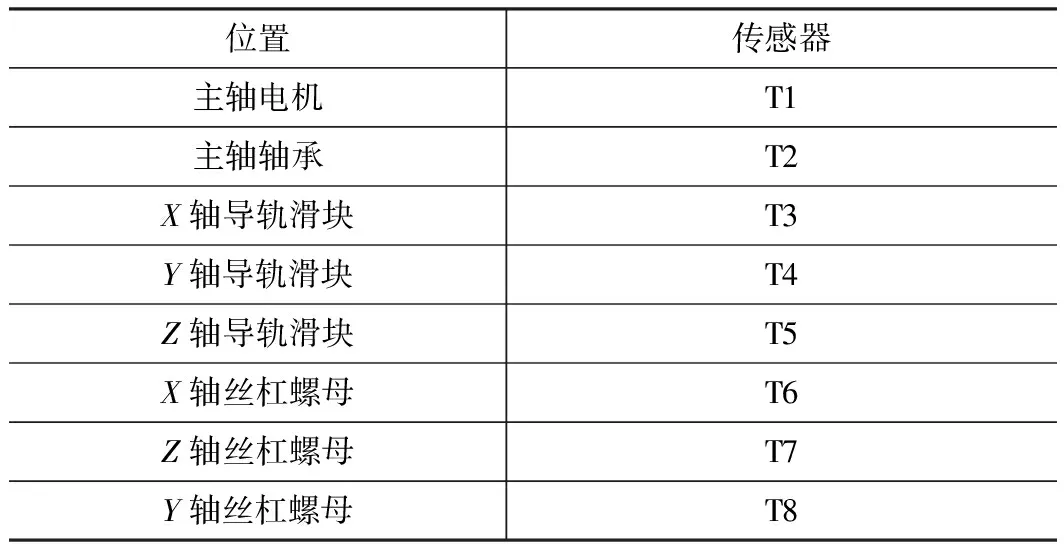
表1 各温度传感器具体位置

机床在230 min达到热稳定状态[17-19]时停止测量，此时机床热源和外界环境热量交换平衡，温度基本不会变化，误差也趋于稳定。温度和热误差变化如图4所示。

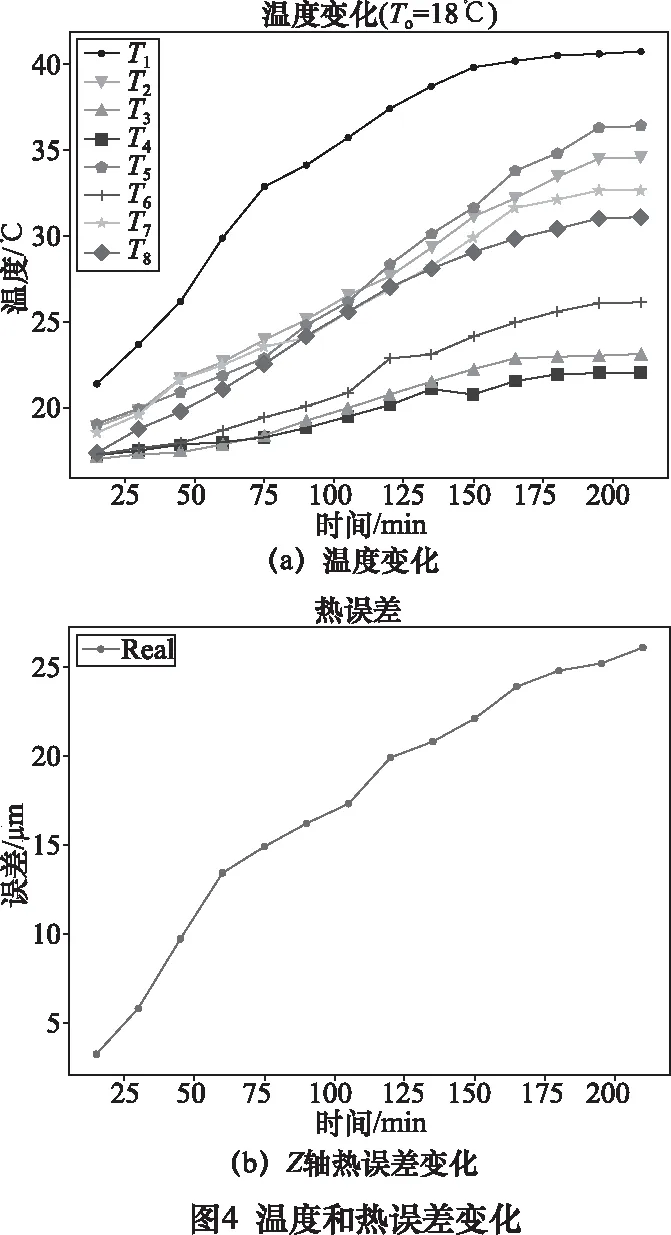
3 温度测点优化

在实验中我们尽可能多地选用了8个温度测点，以防温度场的重要信息丢失导致输入模型的数据不完整，降低了模型预测的准确性。但例如T3和T4的温度变化存在共线性关系，使模型的预测精度降低，同时增大了模型的复杂性和后期处理数据的时间[20-21]。为了尽可能精确筛选温度场中的关键点，我们使用了K-means算法对8个温度测点进行了聚类分析，并从各个聚类中挑选出对热误差影响最大的点作为模型的输入变量。

在此，取K值为3，于此将对热误差相似影响的温度点分成3个簇分别聚集在一起。聚类结果如表2所示。在聚类后，各簇温度变量之间有很强的相似性，为了减少相似温度点之间的耦合效应，我们在构建热误差模型时使用相关系数法在每簇温度变量中选出一个对热误差影响最大的温度点作为模型的输入，温度与热误差斜率之间的相关系数为：

表2 K-means聚类结果

(9)

式中：Tij代表第j次测量中第i个测量位置的温度数据。Ti是第i个测量点温度数据的平均值，kj是第j次测量的定位误差数据的直线拟合斜率，kji是所有斜率的平均值[9]。各温度变量的相关系数如表3所示，相关系数越大，温度测量点与热误差的相关性越强，就越反映热误差的实际变化。结合表2，最后选定T1、T5、T6作为模型的输入变量。

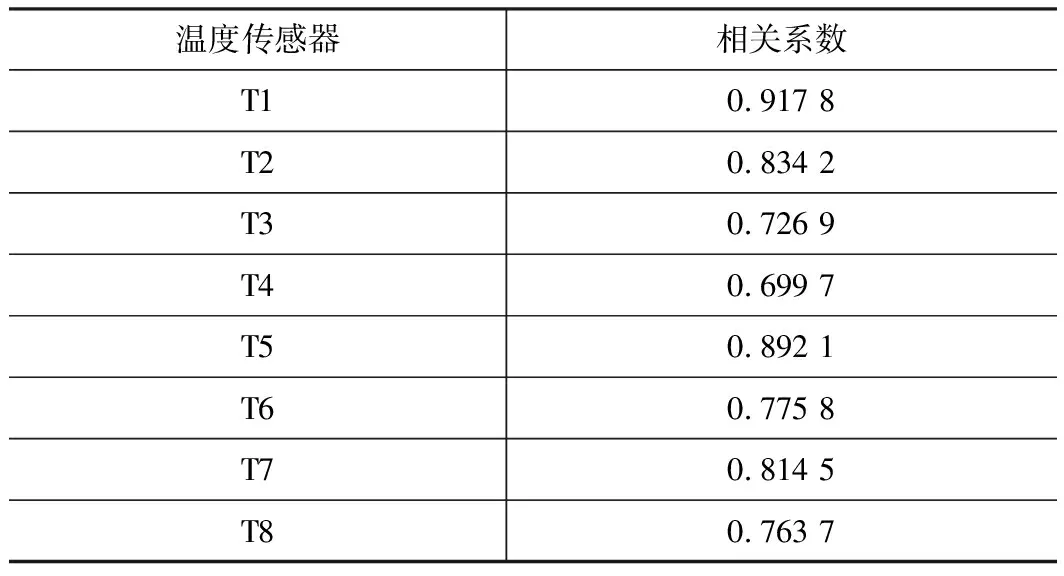
表3 温度变量相关系数

4 验证模型性能

为了验证贝叶斯神经网络(BNN)模型的性能，我们引入了BP神经网络进行对比，从2个方面分析了模型的性能。首先，我们使用一组数据进行误差建模，并比较每种模型的拟合能力。然后，为了比较每个模型的泛化能力，我们使用了在不同工作条件下的另一组实验数据进行预测。

4.1 模型拟合性能分析

将BP神经网络模型结构设为3-7-1，两种模型的学习速率设为0.005，迭代次数为1 000次。模型搭建完成后，把实验数据输入模型中，拟合性能如图7所示，由图5可以看出BP和BNN的拟合精度都很优秀，但BNN的效果更好，为了更为明确得出结论，我们将残差波动幅度ΔEmax、 残差平均值ΔE、均方误差MSE以及预测精度η作为模型性能评估标准。其中预测精度η的计算公式为：

(10)

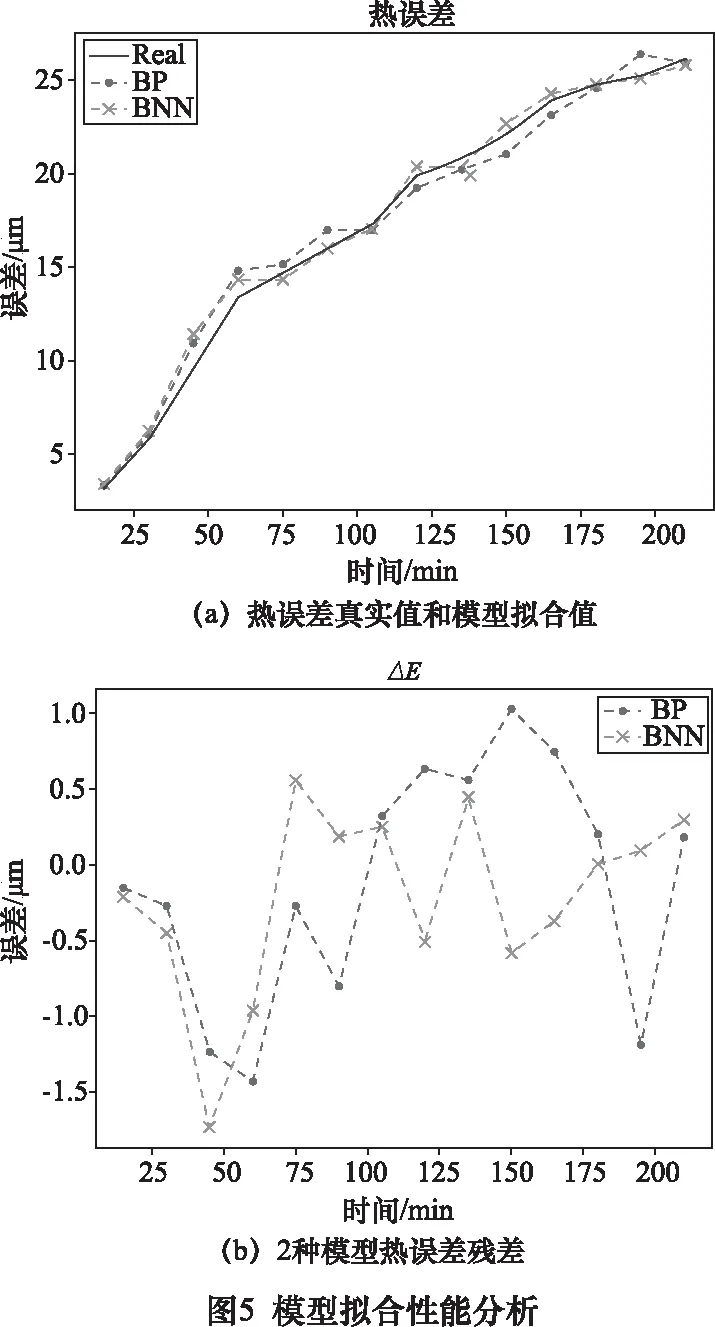
表4 模型性能指标

4.2 模型泛化性能分析

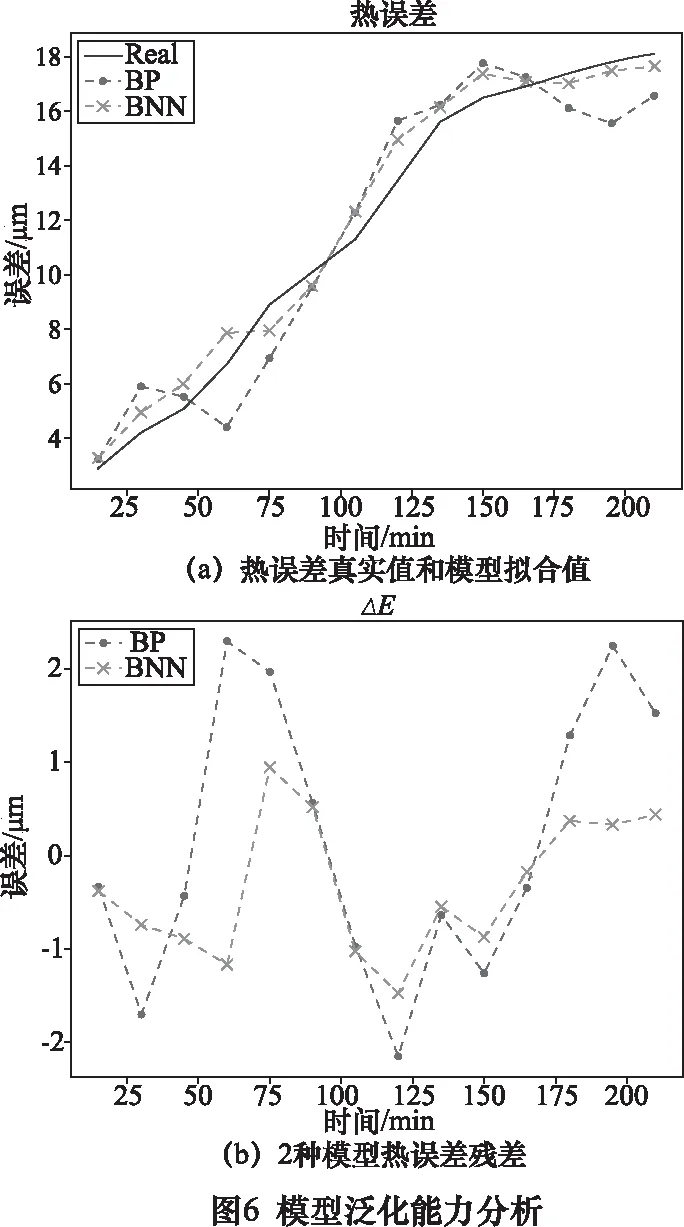
为了验证模型的泛化性能，我们将主轴的转速调整为4 000 r/min，X、Y、Z进给轴以10 m/min做往复运动，以同样的时间频率测量温度和热误差数据，导入模型中，预测结果如图6所示，各项性能指标如表5所示。

表5 模型性能指标

从图表中很容易看出，在改变工况后，BP模型的性能大幅降低，残差波动幅度ΔEmax、 残差平均值ΔE和均方误差MSE数值是BNN模型数值的数倍，其中MSE更是达到了4倍，模型的预测准确率降为72.252 1%，远低于之前的89.292 1%的预测准确率。而BNN模型仅小了3.253 7%，两者的预测准确率相差15.763 8%。由此可见BNN的性能明显高于BP，表明该模型的泛化能力较强。根据热误差建模和验证实验的结果，贝叶斯神经网络的预测性能明显优于BP神经网络，总体精度提高了88.015 9%，这证明了该模型的稳定性和准确性。

5 结语

本文基于贝叶斯神经网络的建模预测机床的热误差，通过测量热误差数据和获得温度敏感点，并将相应的值用作模型的训练，并且可以通过模型预测来获得在每个时刻和每个温度的热误差。实验结果表明，贝叶斯神经网络模型的性能明显优于BP神经网络，其最大预测精度高出了15.763 8%，机床的总体精度提高了88.015 9%。