基于LMD和灰色关联度的故障诊断方法研究*

杨静宗 施春朝 杨天晴 李常芳

(保山学院大数据学院，云南 保山 678000)

随着矿物管道输送技术的不断发展，矿物管道的安全输送已成为备受关注的一大问题。高压隔膜泵作为矿浆输送管道的核心动力源，它是整个系统能否在安全、高效的前提下正常运行的保证。在隔膜泵内部故障中约有40%～60%是由单向阀故障引起的，单向阀健康状态直接影响了矿物管道的输送效率。由于机械设备组件的故障通常伴随着振动信号的变化，通过采集设备的振动信号并对其作出相应的诊断分析是一种较为适宜的方法之一。然而，由于单向阀的运行过程较为复杂，使得提取的振动信号有非平稳性，提取的特征参数有模糊性，给单向阀故障诊断带来了极大的困难。近年来，傅里叶变换[1]、短时傅里叶变换[2]和Winger-Ville分布[3]等传统的分析方法在分析非平稳信号中开展了一定程度的应用，但是上述方法无法有效兼顾非平稳信号在时域与频域的全局与局部特征。基于局部均值分解(local mean decomposition, LMD)[4]的信号处理方法是目前的研究热点，其可把非平稳信号分解为若干个不同频率的PF分量和一个余量，有效地抑制了经验模态分解法(empirical mode decomposition,EMD)[5]产生的模特混叠效应，现已被广泛地应用于多个领域，并取得了良好的效果。林江刚等人[6]提出了基于声发射信号信息熵特征和LMD相结合的分析方法，实验表明，其可以有效识别出低转速状态下的轴承故障。沈超等人[7]通过结合LMD、模糊熵和流形学习的基本思想，对齿轮振动信号进行了故障诊断，证明了所提出方法的有效性。王名月等人[8]提出了一种基于LMD样本熵和径向基神经网络的结构损伤识别方法，并对振动环境下的信号进行了识别。结果表明：该方法对结构损伤的位置和损伤程度都取得了较高的识别精度。王海军等人[9]针对水电站厂房振动监测中易受噪声干扰的问题，采用数据融合和LMD相结合的方法。实验表明该方法可以有效提高信号的信噪比，并准确地提取了振动信息。

传统的神经网络识别方法对样本的数量要求大，训练测试的速度较慢，因而难以适应实际的工程问题。而灰色关联度分析[10-13]作为灰色系统理论的核心内容之一，具有诸多优势：对样本的分布无特别的要求，算法编程简单、计算效率高等等。基于此，本文以隔膜泵单向阀为研究对象，采用基于LMD的方法对单向阀的振动信号展开自适应的分解，进而提取对应的信号故障特征。针对故障模式不易识别的问题，引入灰色关联度，构建单向阀故障诊断模型，为单向阀的故障诊断提供一种新的途径。

1 算法基本原理

1.1 LMD算法原理

LMD方法是由Smith提出的一种信号分解法，其原理是把非平稳信号分解为若各个不同频率的PF分量和一个余量，这些分量由不同尺度的纯调频信号和包络信号相乘得到。若原信号为x(t)，那么分解步骤可以阐述为以下的形式。

(1)计算原信号x(t)的全部局部极值点ni，然后计算相邻局部极值点的平均值mi：

(1)

通过对mi构成的直线展开平滑操作，可以求出x(t)的局部均值函数m11(t)。

(2)求包络估计值：

(2)

同理，通过滑动平均法处理得到包络估计函数a11(t)。

(3)对原信号x(t)进行分离：

h11(t)=x(t)-m11(t)

(3)

(4)对h11(t)进行解调，可得到：

s11(t)=h11(t)/a11(t)

(4)

进一步，通过重复上述步骤可计算得到包络估计函数a12(t)。若s11(t)不是纯调频信号，就需要重复以上迭代步骤，直到符合a1(n+1)(t)=1时，计算出纯调频信号s1n(t)，所以有：

(5)

(6)

迭代终止的条件如下：

(7)

(5)求出包络信号：

(8)

(6)计算第1个PF分量：

PF1(t)=a1(t)s1n(t)

(9)

(7)从原信号中把PF1(t)分离出来，求得新的信号u1(t)得新，然后把它作为原始数据并循环重复上述步骤K次，直到uk(t)成为单调函数。

(11)

将全部PF分量和uk(t)重组，可得到：

(12)

1.2 灰色关联度理论

灰色关联度是描述时间序列变化趋势的接近程度[14-16]。有着对称性、唯一性以及可比性等特点。灰色关联度的基本思想如下：

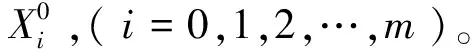
(2)求|s0|、|si|和|si-s0|。具体公式为：

(3)求各灰色绝对关联度ε0i，(i=1,2,…,m)。具体公式为：

2 基于LMD和灰色关联度的单向阀故障诊断模型

基于LMD和灰色关联度的单向阀故障诊断流程如图1所示，详细步骤如下：

(1)选取不同状态下的单向阀振动信号，从中得到不同故障数据，然后通过LMD和EMD分解法将上述样本分解成若干个PF分量和IMF分量。

(2)根据互相关系数法，求出各个PF分量和IMF分量的互相关系数，然后从中选取和原始信号关联度高的PF分量和IMF分量。

(3)从筛选得到的单向阀处于不同状态下的PF分量和IMF分量中分别提取排列熵和奇异值，然后构建特征向量T=[T1,T2,T3,T4,T5,T6]和灰色关联度分析模型。

(4)求出待识别模式与单向阀各运行状态下的标准模式之间的灰色关联度，然后按照灰色关联度最大准则，对上述关联度值的大小进行对比分析，方可完成单向阀故障状态的识别。

3 实验分析

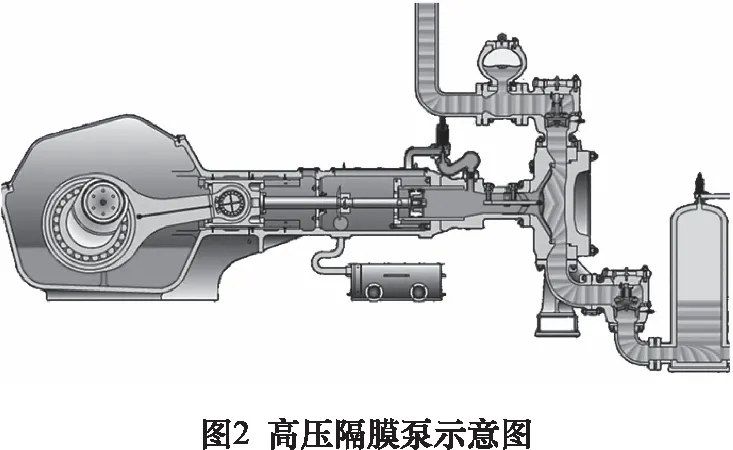
为获得不同状态下的标准模式特征向量，本实验采用中国西部某矿浆输送管线的数据采集系统得到的高压隔膜泵单向阀现场数据作为故障检测的依据。该管线的泵站采用的隔膜泵型号为TZPM，数据采集卡为PXIe-3342型8通道采集卡。所采集到的振动信号包括正常运行、粗颗粒卡阀和磨损击穿3种状态，采样频率为2 560 Hz。首先，选取以上3种状态的样本数据进行信号分解。经过LMD和EMD分解后的单向阀正常运行、粗颗粒卡阀和磨损击穿的结果图如图3～5所示。

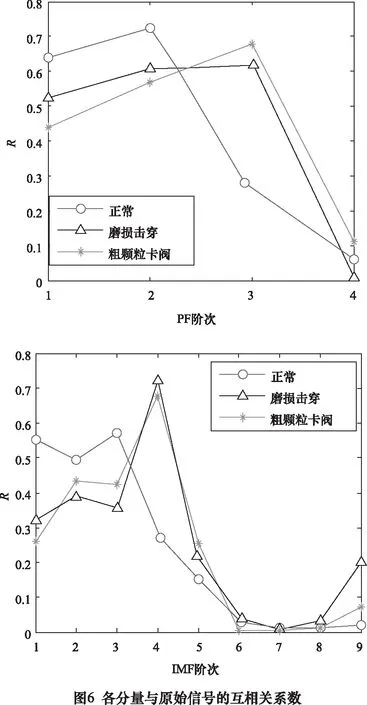
根据互相关准则，计算经过LMD、EMD分解后得到的PF分量和IMF分量与原始信号的互相关程度，所得结果如图6所示。通过分析图6中不同状态下的各PF分量和IMF分量与原始信号的互相关系数值，可知：经过LMD分解后，得到的前3个PF分量与原始信号相关度相对较高。经过EMD分解后，得到的IMF2、IMF3、IMF4分量与原始信号相关度相对较高。基于此，本研究选取上述3个PF分量和3个IMF分量分别进行单向阀不同运行状态下的排列熵和奇异值特征提取，并构造特征向量。为防止数据选取的偶然性，实验分别选取了单向阀在3种状态下的信号各20组，并提取对应的特征向量。然后，将每种运行状态下的10组数据作为标准模式向量，剩余的10组数据作为待检测的模式向量。由于篇幅所限，表1中只展示了单向阀正常、磨损击穿和粗颗粒卡阀状态中的1组数据提取得到的特征向量。其中，T1～T3为提取的排列熵特征，T4～T6为提取的奇异值特征。

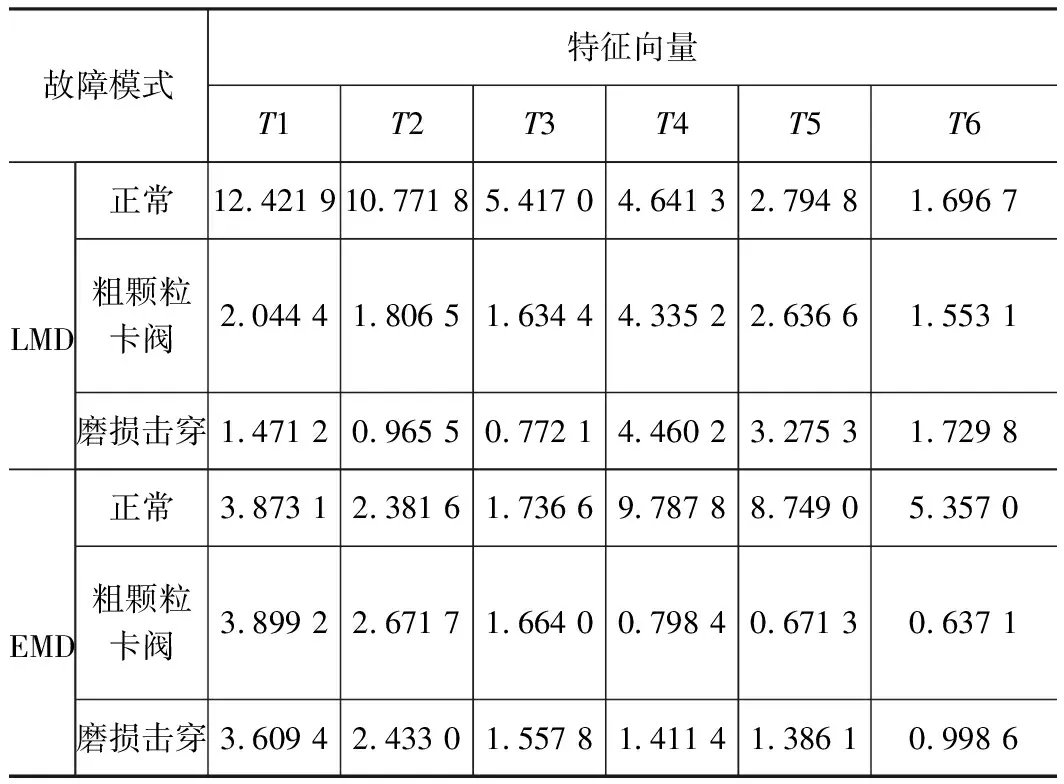
表1 标准模式特征向量

接下来，构建灰色关联度模型，模型计算得到的结果如表2～4所示。表2～4分别为单向阀处于正常状态、磨损击穿和粗颗粒卡阀下的测试数据识别结果。其中，表中的三列数据R1、R2和R3分别为单向阀处于正常、磨损击穿和粗颗粒卡阀状态的关联度值。根据灰色关联度准则，所得到的结果值越大，则代表关联程度越高。从表2可看出，所有第一列R1的关联度值均大于第二列R2和第三列R3的关联度值，由此可以判断出10个测试样本为单向阀正常运行状态下的数据，和实际所处的状态一致。从表3可看出，样本1和样本9中的关联度最大值分别为R3和R1对应的结果值，被错误地识别为粗颗粒卡阀和正常状态。其余数据均被正确识别为磨损击穿状态。从表4可看出，所有第三列R3的关联度值均大于第一列R1和第二列R2的关联度值，由此可判断得到所处的状态为粗颗粒卡阀，识别的结果完全正确。

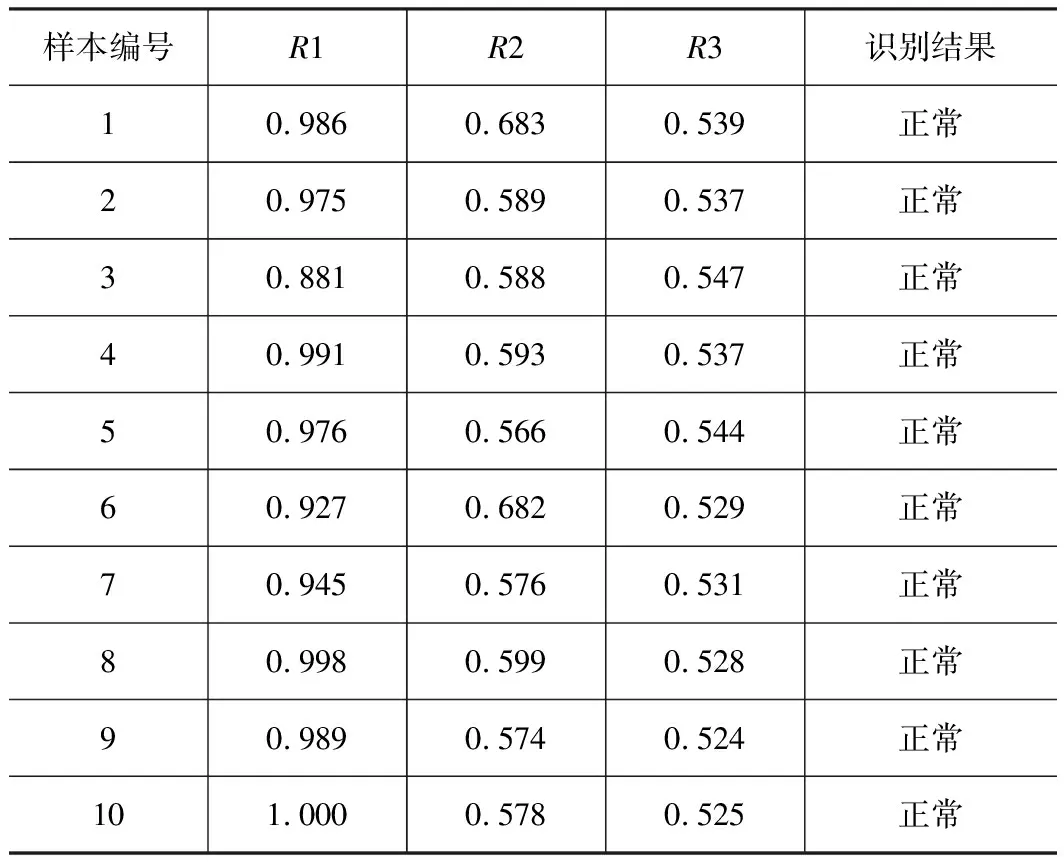
表2 正常状态下基于LMD和灰色关联度的识别结果

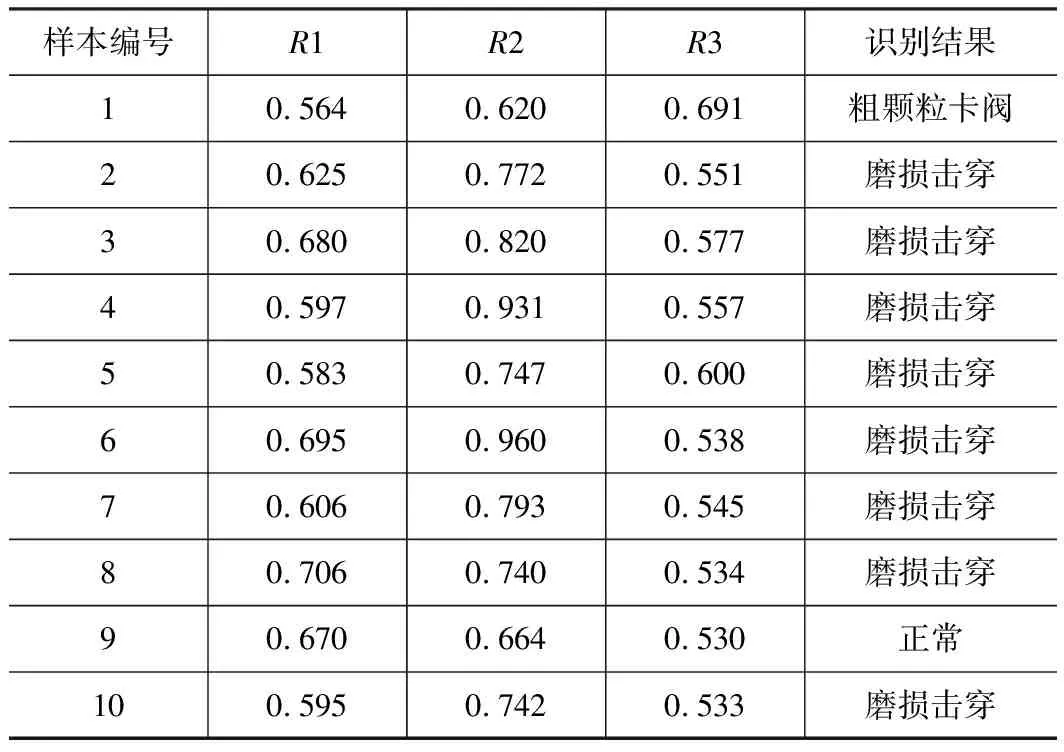
表3 磨损击穿状态下基于LMD和灰色关联度的识别结果

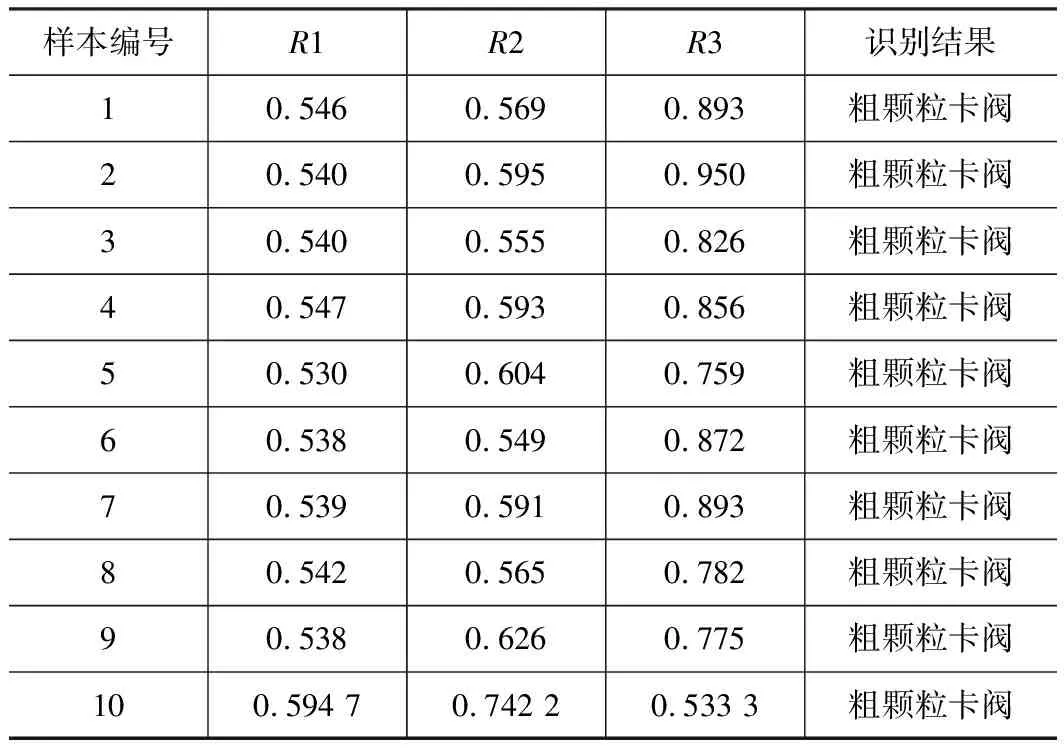
表4 粗颗粒卡阀状态下基于LMD混合特征和灰色关联度的识别结果

为分析经混合特征建模的灰色关联度模型和利用单一特征直接建模的灰色关联度模型的识别效果，本研究另外进行了2次对比实验，实验的识别结果如图7和图8所示。其中，图7和图8分别表示采用奇异值特征、排列熵特征直接建模的识别结果，识别准确率的比较如表4所示。

经过对比分析可知：在基于奇异值特征直接建模的识别中，单向阀正常运行、磨损击穿状态被正确识别的个数均为6个，而粗颗粒卡阀状态被正确识别的个数仅有6个。在基于排列熵特征直接建模的识别中，单向阀正常运行、磨损击穿状态被正确识别的个数分别为7个和5个，粗颗粒卡阀状态被正确识别的个数为8个。基于单一特征建模的方式对单向阀不同类型的故障识别效率不甚理想，识别准确率仅为46.67%和56.67%。在基于混合特征建模的识别结果中，仅有2个测试数据被错误识别，识别准确率达到了99.33%，通过联合混合特征的方式有效地提高了识别效果。

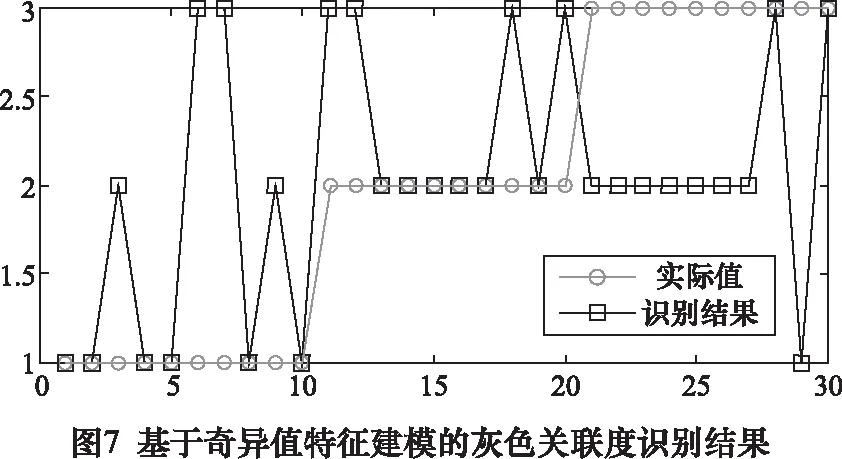
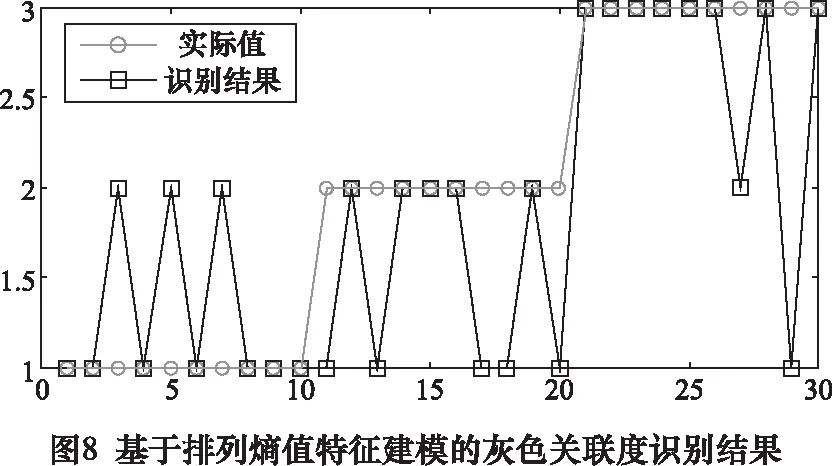
表5 识别结果分析

为进一步比较基于LMD和EMD分解法提取的特征的识别结果，本文同时采用基于LMD和EMD方法提取的混合特征建模的方式进行了灰色关联度识别，结果如表6所示。从中可看出，基于EMD方法提取的混合特征建模的识别结果共有25个数据被正确识别，准确率仅为83.33%，低于基于LMD方法提取的混合特征建模的识别准确率。通过LMD分解得到的PF分量较好地表征了原信号不同的局部特征信息。

表6 基于LMD和EMD的识别结果分析

4 结语

本文针对高压隔膜泵单向阀故障振动信号的非平稳特性，提出了LMD和灰色关联度相结合的单向阀的故障诊断方法。实验过程中，分别利用基于LMD和EMD分解法对单向阀3种不同状态下的信号进行自适应分解，再进一步选取互相关系数相对较高的PF分量和IMF分量，然后提取出对应的奇异值和排列熵作为特征向量。最后，引入灰色关联度理论，构建单向阀故障诊断识别模型。实验结果表明：通过混合特征建模的方式更为全面的表征了信号所含的信息，取得的识别效果要优于基于单一特征建模的方式。其次，由于LMD方法值是通过纯调频信号而得到瞬时频率，而EMD通过对IMF分量进行Hilbert变换获得瞬时频率，因而LMD分解法在迭代次数和抑制端点效应上要优于EMD分解法。同时，通过对基于上述2种分解法所得到的识别结果的比较，可知基于LMD提取的混合特征建模的方式得到的识别准确率更高，能够更加有效地识别小样本条件下的单向阀故障。