BaF2 高压相变行为的第一性原理研究*

田城 蓝剑雄 王苍龙 翟鹏飞† 刘杰

1)(中国科学院近代物理研究所,兰州 730000)

2)(中国科学院大学核科学与技术学院,北京 100049)

通过理论计算研究了BaF2 在高压下的晶体结构及物理性质.结果表明,在3.5 和18.3 GPa,BaF2 依次经历了两次结构相变,相变过程伴随着体积的塌缩,均为一级相变.约15 GP 时,Pnma相晶轴压缩性出现异常,表现为随压强增大,晶轴bo 轻微增加,ao 略微减小.对其电子态密度进行分析发现,在16 GPa 以后,由于F1 原子的py+pz 与px 轨道电子离域,导致其带隙随压强增加而降低.在约20 GPa时,Pnma 相完全转变为P63/mmc 相,相变完成.对BaF2 的拉曼峰位随压强变化进行了计算,为其高压拉曼光谱行为提供了相应的理论依据.计算了P63/mmc 相在不同压强下的声子色散曲线,揭示了其卸压过程中的滞后机制,计算结果还预测该物相至少可以稳定到80 GPa.

1 引言

高压作为一种调控材料性质和发现物质新结构的重要手段,被广泛应用于实验研究中.例如,Snider 等[1]在(267 ± 10)GPa 压强和(287.7 ±1.2)K 温度下实现了C-S-H 材料的室温超导转变;Xia 等[2]利用高压手段对WSe2-MoSe2二维异质结层间距和层间耦合作用进行了调控;徐波和田永君[3]在高温高压条件下合成了纳米孪晶结构的立方氮化硼和金刚石块材超硬材料.随着金刚石对顶砧(DAC)技术的不断发展,材料在高压下的行为正受到越来越多的关注.

CaF2,SrF2,BaF2是一类常见的碱土金属氟化物,由于它们具有独特的光学和电学性质而受到了广泛的关注,如BaF2具有优异的闪烁性能,可用于探测γ射线[4].一方面,该类材料结构简单,常温常压下均为立方萤石结构,它们在较窄的应力范围内有较大的应变,对于发展高压状态方程很有帮助.另一方面,了解这些材料高压引起的相变也有助于理解地球深处的材料相变[5].已有实验研究表明,高压下它们会经历两次相变,相变顺序均为(立方萤石结构)-Pnma(α-PbCl2型结构)-P63/mmc(Ni2In 结构)相,相应的阳离子配位数由8 增加到9 再增加到11[6-9].由于BaF2相变压强较低,在实验上更容易实现,是研究这类物质高压行为的范例,其结果可为其他碱土金属氟化物的高压行为提供参考.拉曼光谱[10-12]和XRD[6,9]研究表明,BaF2的相变压强分别为约2.3—3.0 GPa 和14—15 GPa.在第二次相变压强附近,Pnma相晶轴压缩性出现异常,并且在卸压过程中两种高压相均存在滞后现象,其中Pnma相在卸压后可与相共存.

理论计算可以不受实验技术及条件的限制,在较大的压强范围内对材料的性质和结构做出合理的预测[13,14].已有学者对BaF2的高压相变行为进行了一定的理论计算研究.计算结果表明,BaF2两次相变压强分别为2.83—5.10 GPa,11.2—15.0 GPa[4,15-17].其中,Ayala[4]采用shell-model 方法,通过对BaF2晶格常数、原子位置、介电常数以及高压相三棱柱倾角的计算,得出Pnma-P63/mmc完全相变压强点为17 GPa;Kanchana 等[17]利用紧束缚线性muffin-tin 轨道法,指出在33 GPa 压强下,电子从氟的p 轨道转移到钡的s 和d 轨道,从而导致BaF2的P63/mmc相发生金属化;然而,Jiang 等[16]利用原子线性轨道方法,引入半经验参数对带隙进行修正后,指出在50 GPa 压强下BaF2仍不会发生金属化;Yang 等[15]基于密度泛函理论,利用CASTEP 软件对高压下BaF2的结构稳定性、电子结构、弹性性质进行了理论研究,他们的计算表明,在高达210 GPa 的压强下,不会发生能带交叠的金属化现象.目前,BaF2卸压过程中P63/mmc相的滞后现象还缺少相应的理论解释.此外,BaF2带隙随压强变化的行为还存有争议,而且其高压拉曼光谱行为的研究也比较少.因此,本文利用第一性原理对BaF2的拉曼峰位及其P63/mmc相的声子色散曲线随压强的变化进行计算,以期对其高压拉曼光谱行为和卸压过程中P63/mmc相的滞后现象进行解释,并结合晶格常数和带隙计算,对其高压行为进行较为系统的理论研究.

2 计算方法

本文计算基于密度泛函理论(DFT),采用投影缀加波(PAW)方法[18],利用VASP[19]软件进行计算.交换关联势选用广义梯度近似(GGA)的PBE 版本[20].经过收敛性测试,对于BaF2的3 种物相,截断能均设为600 eV,能量和力的收敛标准分别为10—8eV 和0.001 eV/Å.布里渊区K点网格均采用Gamma 取点方式,对于BaF2的Pnma和P63/mmc相,网格密度分别为7×7×7,7×11×6,11×11×9.

由于理论计算是基于T(温度)=0 K 的,故吉布斯自由能(G)等于焓(H),即G=H=E+PV,其中E,P,V分别为体系的内能、压强、体积.所以在给定压强下,焓值越低的结构越稳定.于是，可以由计算结果做出BaF23 种物相的焓(H)-压强(P)关系图,并由此推测相变压强[15,21-25].

3 结果与讨论

3.1 BaF2 的结构稳定性

为了判断相变压强,在一系列给定压强下对BaF23 种物相进行结构优化,其中,相在0 GPa 下优化后的晶格常数为ac=6.281 Å,原子位置为Ba(0,0,0),F(0.25,0.25,0.25);Pnma相在12 GPa 下优化后的晶格常数分别为ao=6.284 Å,bo=3.926 Å,co=7.791 Å,原子位置为Ba(0.2452,0.25,0.3814),F1(0.0391,0.25,0.6820),F2(0.1496,0.25,0.0668);P63/mmc相 在32 GPa 下优化 后的晶格常数为ah=bh=4.183 Å,ch=5.260 Å,原子位置为Ba(0.3333,0.6667,0.25),F1(0,0,0),F2(0.3333,0.6667,0.75).以上晶格常数计算结果均与实验测量值[10]符合较好,证明本工作的计算模型合理.

图1 为BaF23 种物相相对焓差随压力的变化,其中插图为18—19 GPa 的局部放大图.可以看出,的结构相变压强分别为约3.5 和18.3 GPa.对 于Pnma和P63/mmc相,当压强达到20.0 GPa 后,两相焓值几乎相等,表明20 GPa 以后这两相可以共存[26],或者存在着连续交替相变[4].

图1 BaF2 相对焓差随压强的变化Fig.1.Variation of enthalpy difference with pressure for BaF2.

图2 为BaF2相对体积随压强的变化.可以看出,当压强达到3.5 GPa 时,材料经历第一次相变,此时相对体积发生突变,急剧塌缩约8.68%;而当压强达到第二次相变压强点时(约18.3 GPa),BaF2的相对体积变化较小,仅仅塌缩约1.35%.两次相变过程均伴随着体积塌缩,表明均为一级相变.

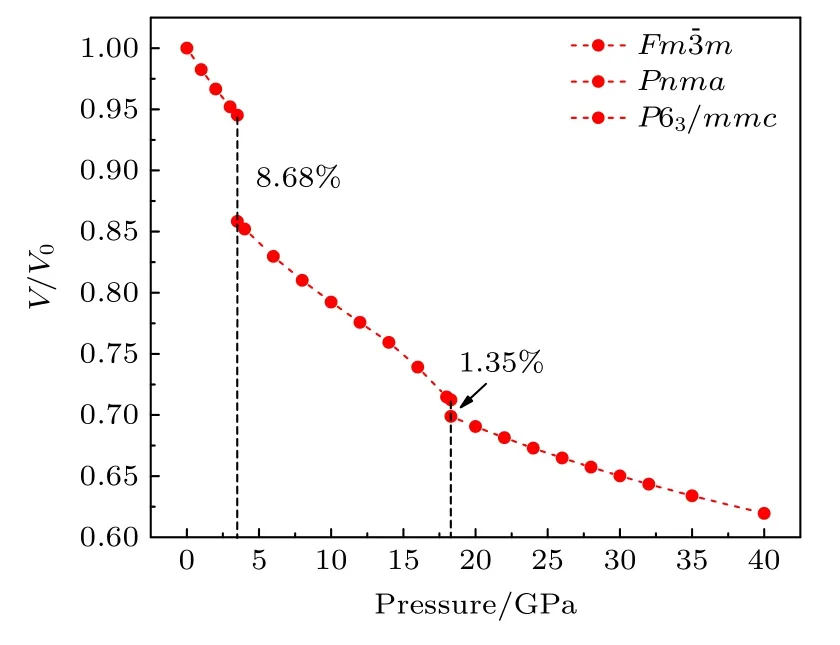
图2 BaF2 的相对体积随压强的变化Fig.2.Relative volume (V/V0)variation of BaF2 as a function of pressure.

由于P63/mmc(ah,ch)可以视为Pnma(ao,bo,co)的一个supergroup[27],当两相晶格常数满足,并且Pnma相中的原子移动到相应位置时,可以认为Pnma相完全变成了P63/mmc相[4,28],由此可以推测完全相变压强点.所以本文对BaF2的,Pnma(ao,bo,co),P63/mmc(ah,ch)相的晶格常数随压强变化进行了分析.为了更好地比较晶格常数之间的关系,利用上述等式关系对晶格常数做了一定的处理,然后画出其随压强的变化图.

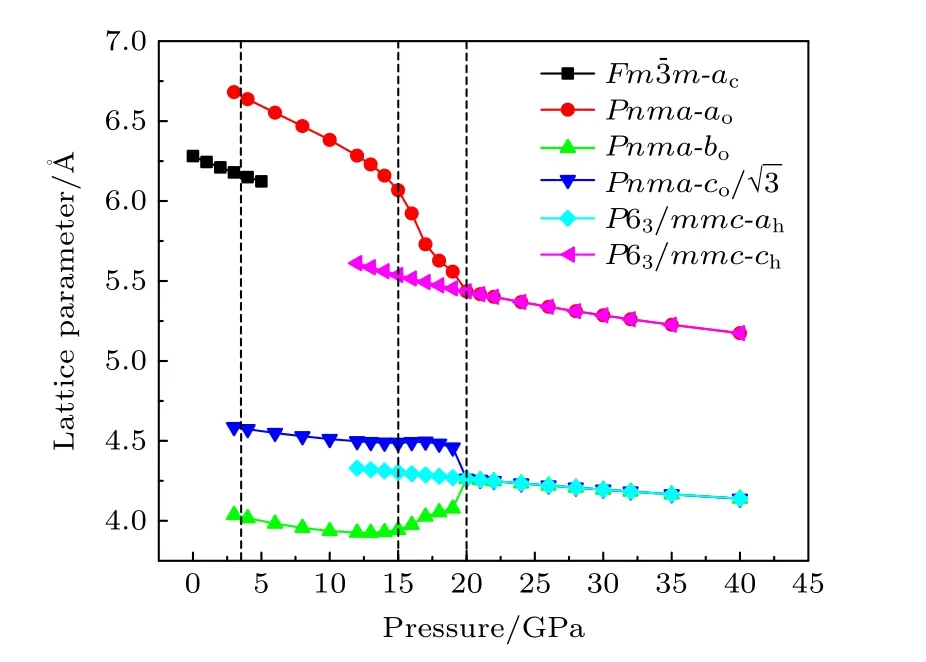
图3 BaF23 种物相晶格常数随压强的变化Fig.3.Evolution of the lattice constants of BaF2 with three structures under pressure.

当压强达到约20 GPa 后,ao=ch,bo=ah,,此时可以认为Pnma完全弛豫为P63/mmc相,即发生了完全相变.在对CaF2[26],BaF2[4],CaH2[29],CeO2以及ThO2[30]等Pnma相和Li2O[31],Mg2Si[32],Li2S,Na2S,K2S[28]等反Pnma相的计算中,均发现晶轴压缩性随压强变化会出现这种类似现象.也许对于Pnma-P63/mmc结构相变的材料,这种行为并不是特例.

3.2 BaF2 的晶格动力学性质

为了分析BaF2的高压拉曼光谱行为以及对其P63/mmc相在卸压过程中的滞后现象进行理论解释,本文基于密度泛函微扰理论[34](DFPT),利用VASP[19]和phonopy[35]软件,对BaF23 种物相的拉曼峰位以及P63/mmc相的声子色散曲线随压强的变化进行了计算.

利用计算得到的布里渊区中心(Γ)声子特征向量来推导声子模的对称标记,由群理论[36]分析,BaF23 种物相的拉曼振动可以分别表示为

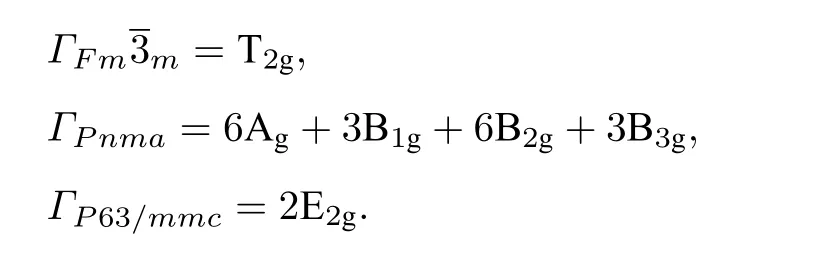
表1 给出了计算所得BaF2的Pnma相在10 GPa压强下的拉曼峰位,其中190.6—363.8 cm—1的波数范围与实验所测的6 个拉曼峰(约210—380 cm—1)较为一致[10].图4(a)和图4(b)分别为相T2g模和P63/mmc相2E2g模拉曼峰随压强变化的关系图.在0 GPa 时,相T2g峰位约为235.8 cm—1,与实验值(240—242 cm—1)较为符合[10,11].相对于其他计算 (约216 cm—1)[37],本文的计算结果更接近实验值.随着压强增大,峰位向高波数方向移动,其斜率约为6.36 cm—1/GPa,略低于实验值7.6—8 cm—1/GPa[10,11].

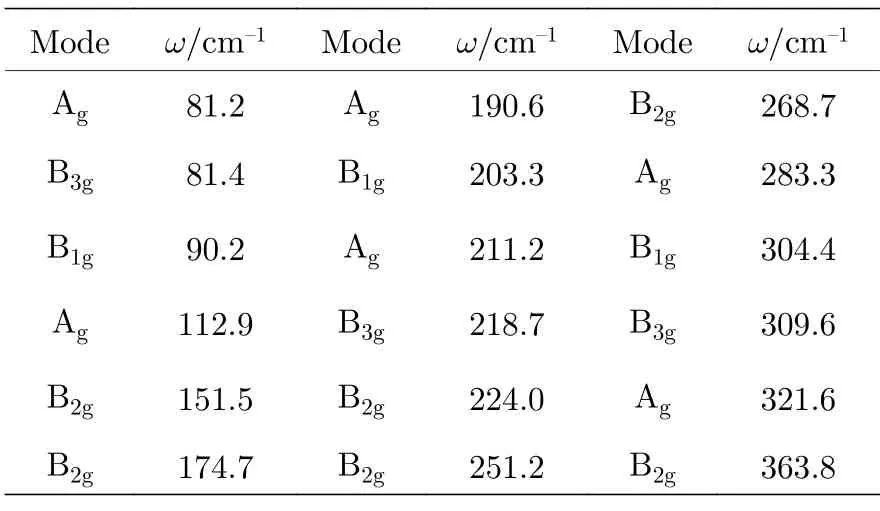
表1 10 GPa 压强下Pnma 结构BaF2 拉曼峰位计算结果Table 1.Calculated Raman shift of Pnma structure BaF2 under 10 GPa.

图4(b)为P63/mmc相的两个E2g模随压强的变化.在14 GPa 时,两个拉曼峰分别位于约95.5和366.7 cm—1;80 GPa 时,分别位于约123.0 和537.8 cm—1,与实验(14.1 GPa 时95 和325 cm—1,77.1 GPa 只有一个约525 cm—1的高频模)[10]在相应压强下所得结果基本一致.由图4(b)可知,高波数的振动模对压强的变化更为敏感,两个振动模随压强变化均表现出非线性:压强越低,非线性程度越小,压强越高,非线性程度越高.所以实验上,在较小的压强范围内对拉曼峰随压强的变化关系进行线性拟合是可行的,但是当压强范围较大时,进行线性拟合的做法似乎不太合适.

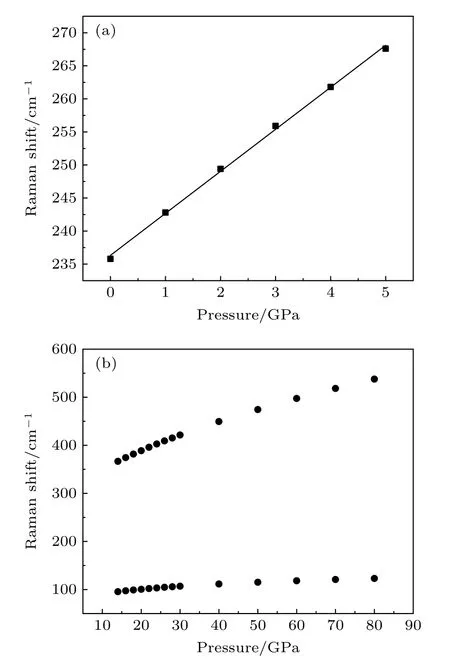
图4 BaF2 (a)Fm m 结构T2g 模和(b)P63/mmc 结构2E2g模拉曼峰位随压强的变化Fig.4.Raman shift as a function of pressure for (a)T2g of Fm m and (b)2E2g of P63/mmc.

图5 为不同压强下P63/mmc相的声子色散曲线.在14 GPa 时,整个布里渊区没有虚频,表明结构此时是动力学稳定的,但是M点(0.5,0.0,0.0)声学支声子有软化的迹象;12 GPa 时,在M点出现虚频,表明此时结构是动力学不稳定的.图6 给出了M点声学声子频率随压强的变化.可以看出,声子频率软化至0 THz 的压强约为13.5 GPa.这说明卸压过程中,P63/mmc相可以存在至13.5 GPa,由此可以解释卸压过程中,该相存在滞后现象(加压过程,18.3 GPa 时才出现P63/mmc相),滞后约4.8 GPa.

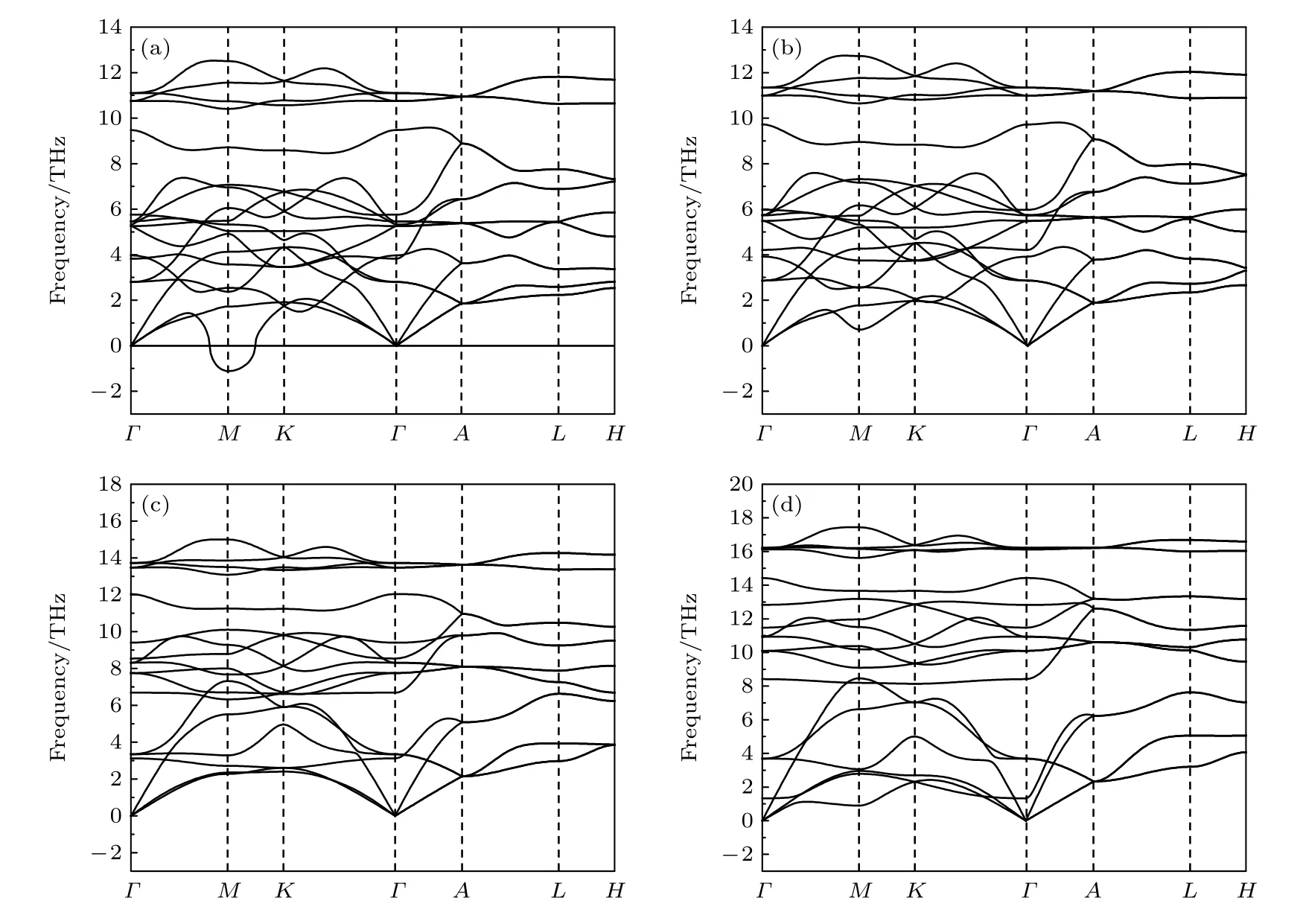
图5 不同压强下BaF2 的P63/mmc 相声子谱 (a)12 GPa;(b)14 GPa;(c)40 GPa;(d)80 GPaFig.5.Phonon dispersion curves for P63/mmc structure of BaF2 at different pressures:(a)12 GPa;(b)14 GPa;(c)40 GPa;(d)80 GPa.

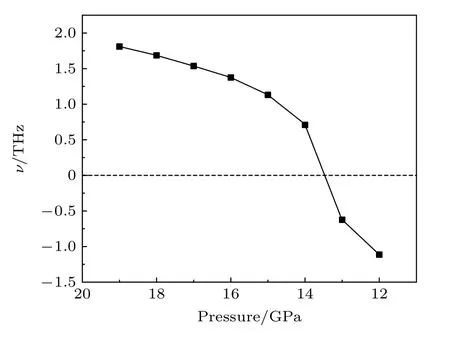
图6 P63/mmc 结构M 点声学支声子振动频率随压强的变化Fig.6.Phonon frequencies at M point as a function of pressure for P63/mmc structure.

当压强为80 GPa 时,整个布里渊区不存在虚频,表明BaF2的P63/mmc相至少可以稳定到80 GPa,与实验所得77 GPa 的结论一致[10].对比40 GPa 时的声子色散曲线可以发现,此时M点声子似乎又出现了软化迹象,故预计超过80 GPa 后,P63/mmc相开始不稳定,可能会再经历一次相变,例如转变为BaH2的AlB2结构[38],或Luo 等[39]所预测的P-3m1 结构.

3.3 BaF2 的带隙随压强变化关系

本文还对BaF23 种物相的带隙随压强的变化进行了计算,结果如图7 所示.0 GPa 时,相带隙约为6.61 eV,低于实验值[40]10 eV,这可以被认为是密度泛函对带隙的计算误差.当达到第一次相变压强时,结构转变为Pnma相,带隙突然增加约0.22 eV,且带隙刚开始与压力呈正相关关系,但当压强为约16 GPa 时,带隙开始减小.在18.3 GPa 时,P63/mmc相的带隙约为5.61 eV,相比于同压强下Pnma相的带隙,降低约1.11 eV.BaF2的这种带隙随压强的变化行为与其他碱土金属氟化物的行为一致[26,41-43],本文的结果也与Kanchana 等[17]的结论一致,而在文献[15]和文献[44]中作者指出,BaF2的Pnma相的带隙随压强增加是一直增加的,没有出现降低的情况,但他们并没有给出相变点附近的带隙数据,也没有对材料的晶格常数随压强变化做出分析.可能是由于带隙突变的压强范围较小,所以导致其他学者忽略了这一点.

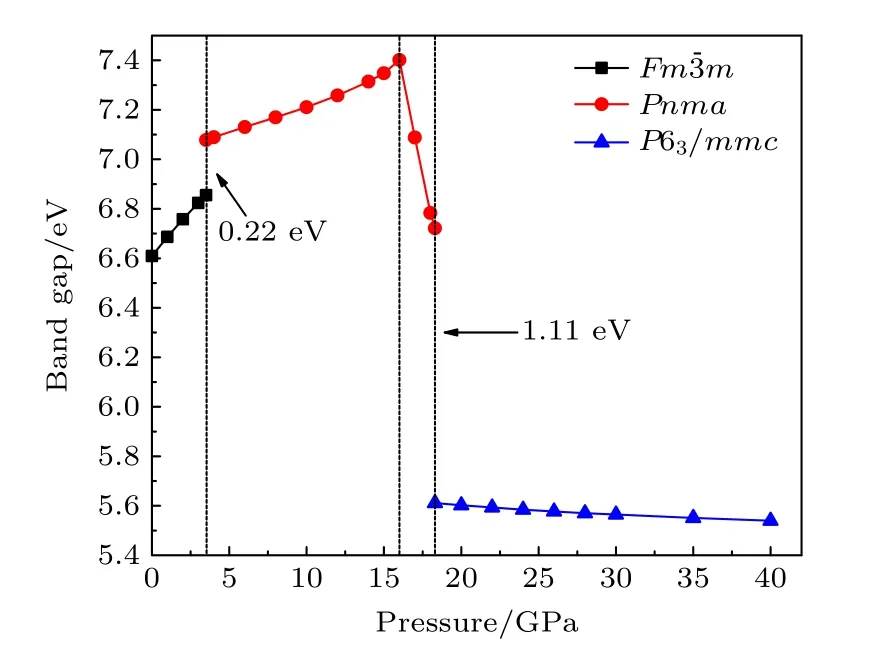
图7 GGA 泛函计算BaF23 种物相带隙随压强的变化Fig.7.Band gap as a function of pressure for three structures with GGA of BaF2.

对于晶体材料而言,随着压强增加,原子间距离减小,电子云重叠程度增加,造成晶体材料中存在离子键向共价键转变的趋势,从而导致带隙增加;当压强足够大时,电子不再属于单个原子或者某个键,形成离域电子,导致带隙减小[26,45].为了进一步分析Pnma相带隙降低的原因,本文对其电子态密度随压强的变化进行了计算,结果如图8 所示.价带顶主要由F 的p 轨道电子贡献,导带底主要由Ba 的d 轨道电子贡献,压强增大时,态密度所在区域能带宽度有所增加,当压强由5 GPa 增加到16 GPa 时,导带部分向高能量方向移动,带隙变宽;16—18 GPa 时,导带部分又向低能量方向移动,导致价带和导带靠近,使带隙变窄.图9 为不同压强下Pnma相中F1(位置见3.1)原子在px与py+pz轨道上的投影电子态密度,16 GPa以后,F1 原子的px和py+pz轨道电子在费米面附近出现了明显的分离,在相变压强下,P63/mmc相F 原子的pz与px+py轨道电子也出现了分离,且更为明显,与CaF2[42]的结果类似,这也可以解释其带隙的减小.

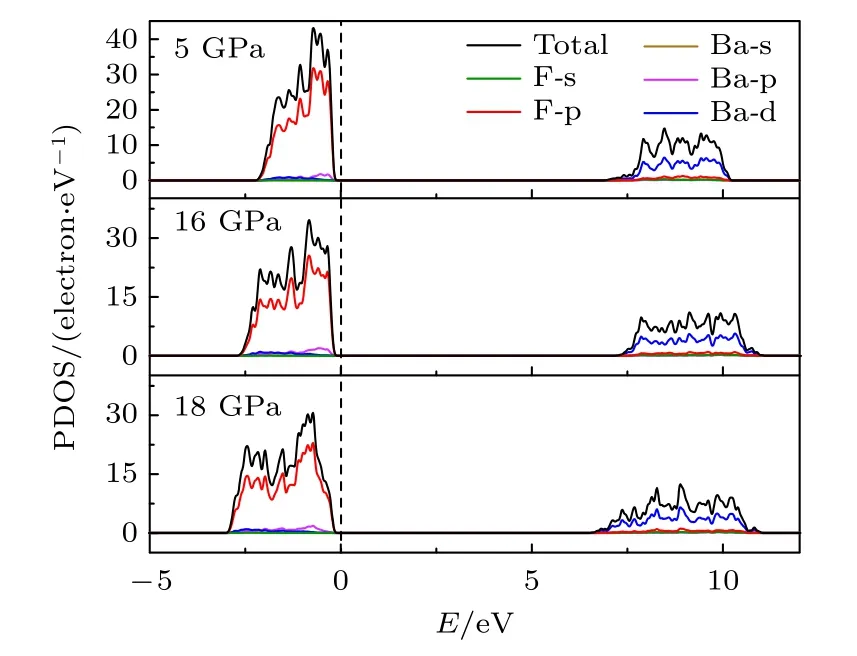
图8 Pnma 相电子态密度随压强的变化Fig.8.DOS of BaF2 for Pnma structure at different pressure.

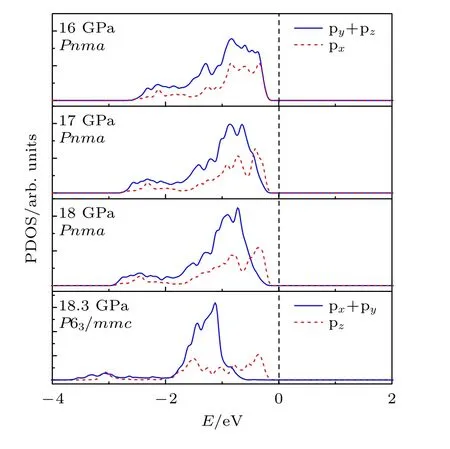
图9 Pnma 相F1 原子投 影电子 态密度(PDOS)随压强的变化Fig.9.Projected DOS onto py+pz and px orbitals of F1 atoms for Pnma and P63/mmc structure.

根据已有的CaF2[26,42],SrF2[43],Na2S[28],ThO2和CeO2[30]等材料的计算结果,可以发现这些材料Pnma相的带隙随着压强增加,均为先增加再减小.仔细观察文中给出的晶格常数以及带隙随压强变化的关系图后,可知Pnma相带隙减小的位置处于相变前兆现象的压强范围内,此时Pnma相开始向P63/mmc相弛豫,而P63/mmc相的带隙比较小,所以Pnma相的带隙减小也是可以理解的.

对于P63/mmc相,其带隙随压强增加而降低,对数据进行线性拟合,得到斜率为—0.0033 eV/GPa,如果采用文献[23]中所提出的外推法推测其金属化压强,则压强应达到约1700 GPa 以上,而结合声子谱分析,可知BaF2的P63/mmc相在80 GPa以后可能是不稳定的,所以采用外推法来寻找材料金属化压强点的做法还有待商榷.

4 结论

第一性原理计算表明,BaF2在高压下会经历两次一级相变,相变压强分别为3.5 和18.3 GPa.对于Pnma相,在压强约为15 GPa 时,晶轴压缩性出现异常,随压强增加其晶轴bo轻微增加,ao略微减小.16 GPa 以后,由于F1 原子px与py+pz轨道电子离域而导致其带隙减小.当压强约为20 GPa 时,Pnma相完全转变为P63/mmc相.另外还计算了BaF2的拉曼峰位随压强的变化关系,给出了Pnma相在10 GPa 下的拉曼峰,为实验上利用拉曼光谱指认该相提供了理论依据.对于P63/mmc相的两个E2g模式,其高波数拉曼峰对压强变化更敏感.通过分析不同压强下的声子色散曲线,指出卸压时P63/mmc相存在滞后现象,滞后约4.8 GPa,并且该物相至少可以稳定到80 GPa.