Rashba效应和Zeeman效应对各向异性量子点中束缚磁极化子性质的影响

红兰 戈君 双山 刘达权

(呼伦贝尔学院物理与电子信息学院,呼伦贝尔 021008)

采用Pekar 变分法和幺正变换相结合的方法研究了各向异性量子点中束缚磁极化子的Rashba 效应和Zeeman 效应.通过理论推导,得到束缚磁极化子基态能量的表达式.讨论了极化子基态能量与横向有效受限长度、纵向有效受限长度、磁场回旋共振频率、库仑束缚势的关系.由于晶体结构反演非对称性和时间反演非对称性,极化子能量发生Rashba 自旋轨道分裂和Zeeman 分裂.在强、弱磁场下,分别讨论了Zeeman 效应和Rashba 效应在能量分裂中所占的主导地位.由于声子和杂质的存在,极化子比裸电子态更稳定.

1 引言

人们应用电子的电荷特性开创了微电子学,使各种基于电荷特性的半导体微电子器件走进人们的日常生活[1,2].近年来,自旋电子学成为了物理学中最热门的研究领域之一,它不但是一个基本的物理问题,同时还有广阔的应用前景[3-6].自旋电子学的研究基础是不同自旋态的电子在材料中的浓度不同,也就是说,自旋在能量上分裂了.这种分裂主要是由于结构反演非对称所导致的Rashba效应和晶体反演非对称所导致的Dresselhaus 效应引起的[7].目前,自旋电子学的一个重要分支是研究量子阱、量子点、量子线或半导体异质结中的Rashba 和Dresselhaus 自旋轨道耦合效应,这些效应可用于自旋晶体管、自旋滤波器和自旋波导等电子器件[8].而在窄禁带半导体中Rashba 效应占主导地位,Dresselhaus 效应可以忽略不计.

Datta 和Das[9]在1990年首次提出了基于控制电子自旋的晶体管原理,自从Datta 的文章发表以来,世界上许多学者对低维量子系统中的Rashba效应进行了实验和理论研究[10-13],尤其是在量子点系统.如,Governale[14]从理论上研究了自旋轨道耦合对量子点中电子结构的影响,利用自旋密度泛函理论计算了量子点的基态性质与电子数的关系.考虑Rashba 自旋轨道相互作用的影响,Li 等[15]研究了抛物量子点中电子-体纵光学声子强耦合相互作用,采用Pekar 变分法计算了极化子基态能量,在Rashba 效应的影响下,极化子的基态能量发生分裂.采用相同的方法,他们还研究了抛物量子点中束缚磁极化子的性质[16].然而,外加磁场也能使电子能量发生分裂,此分裂称为Zeeman 分裂,它要求时间反演不对称.因此,Rashba 自旋轨道相互作用引起的分裂并不是一个简单的分裂,有时会掺杂Zeeman 分裂.虽然两种分裂的方向不同,但如何区分它们的贡献仍存在一定的难度.在外磁场作用下,一些研究者同时研究了量子点系统中的两种分裂.例如:Lee 和Spector[17]研究了Rashba 自旋分裂和磁场对抛物量子点中电子能级的影响.结果表明,在没有磁场的情况下,随着Rashba 参数的增大,电子能级出现双重简并且逐渐降低,当存在磁场时,随着Rashba 参数和磁场的增大,简并解除,自旋态的能量分裂增大.Bandyopadhyay 和Cahay[18]导出了具有铁磁接触的各向异性量子点中总自旋分裂能的表达式,铁磁接触产生的磁场引起了量子点中电子态的Zeeman 分裂.结果表明,由于各向异性量子点中Rashba自旋轨道耦合的非消失性,在横向电场作用下Zeeman分裂可以得到很好的调谐.迄今为止,人们对电子系统的Rashba 效应和Zeeman 效应已做了大量的研究工作,但在极化子领域研究的却较少,尤其是当Rashba 效应和Zeeman 效应同时存在时研究的更少[19].本文将研究Rashba 效应和Zeeman 效应对各向异性量子点中束缚磁极化子性质的影响,并在强、弱磁场作用下,分别对Zeeman效应和Rashba 效应的主导地位进行分析.

2 理论模型

强耦合极性晶体中运动的电子被介质包围并与类氢杂质耦合,由于声子场和极性晶体的边界效应,电子在每个方向的运动都是量子化的.建立空间直角坐标系o-xyz,使oz轴位于量子点的中心轴上,假设电子在z方向和x-y平面上受到不同抛物势的限制,在z方向施加磁场B,矢势用A=(-By/2,Bx/2,0)表示.各向异性量子点中电子-声子相互作用系统的哈密顿量可写为

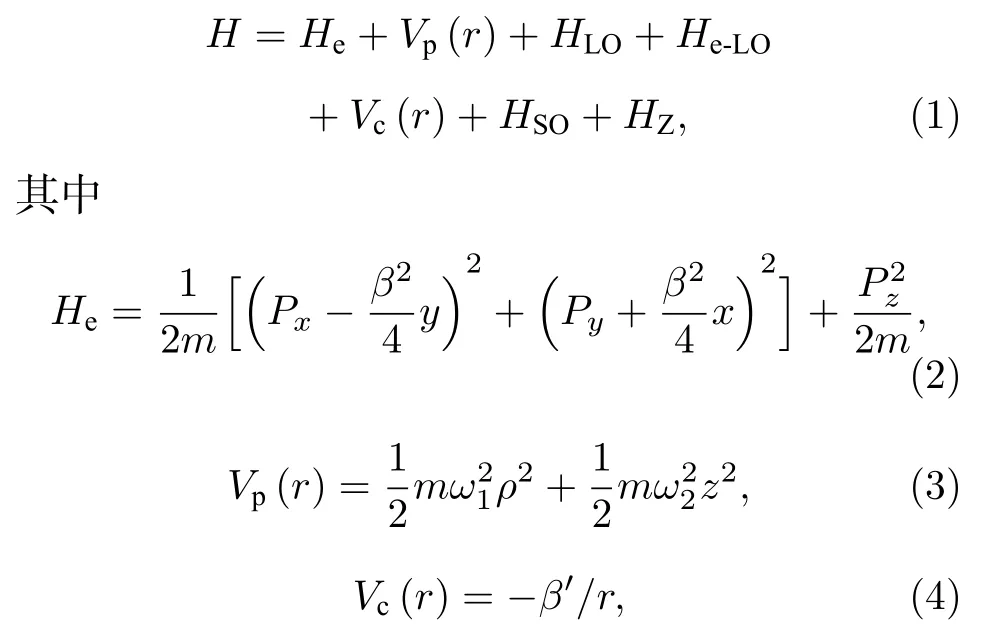
式中,He代表电子动能,m是电子带质量,β2=2eB/c,Vp(r)表示x-y平面和z方向的三维受限势,ω1和ω2被定义为各向异性量子点的横向和纵向受限强度,r=(ρ,z)是电子的位置矢量,Vc(r)是库仑束缚势.

哈密顿量中:

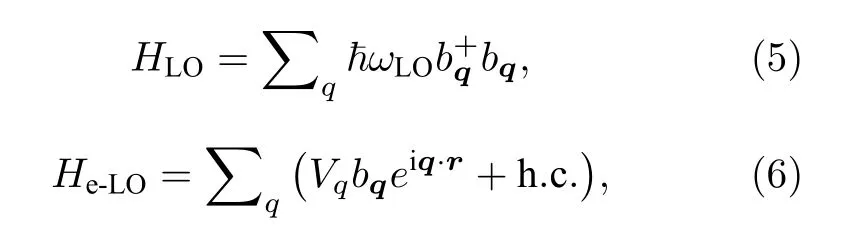
分别表示体纵光学声子场能量和电子与体纵光学声子的相互作用能.(6)式中Vq定义如下[20]:

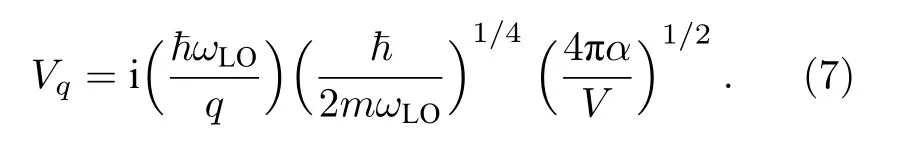
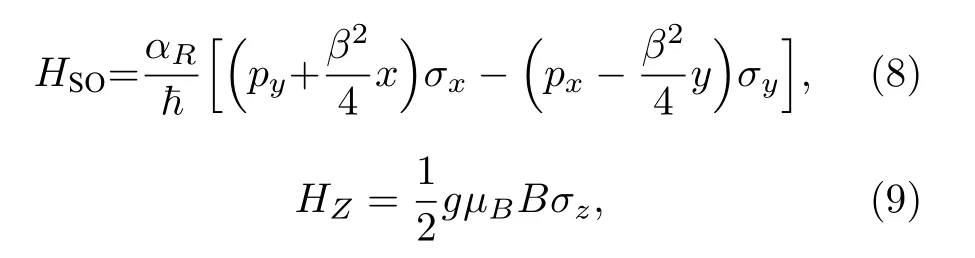
分别在+z—极化自旋和—z—极化自旋之间引入Rashba 自旋轨道相互作用和Zeeman 分裂.σx,σy和σz分别是泡利矩阵矢量在x方向、y方向和z方向的分量.g是朗德因子,µB=eℏ/(2m0c)是玻尔磁子(m0是裸电子质量),Rashba 自旋-轨道耦合常量αR受多种因素的影响.将库仑束缚势展开为傅里叶级数形式:

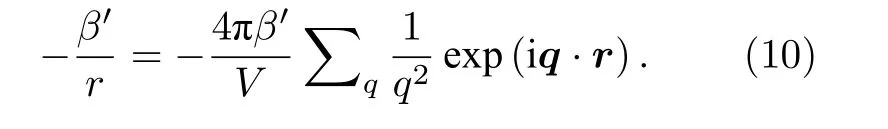
为了简化系统的哈密顿量,对方程(1)进行幺正变换,引入幺正变换算符:

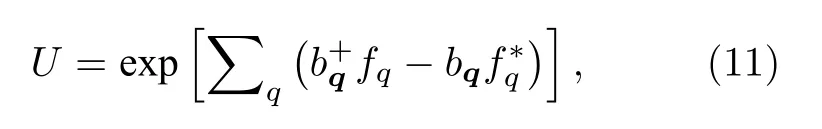
其中fq是变分函数,可通过对能量求变分取极小求得,变换后的哈密顿量为

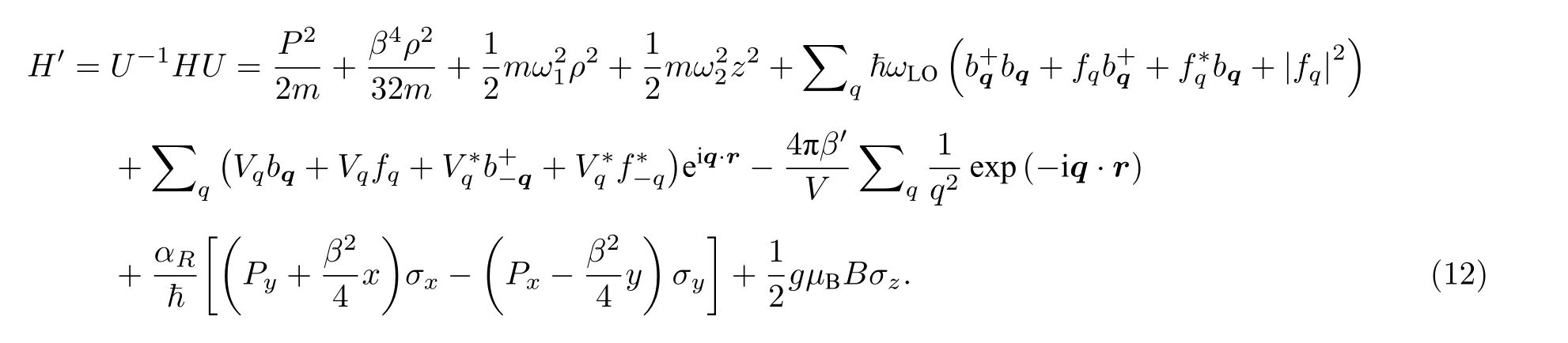
系统的基态尝试波函数选为:

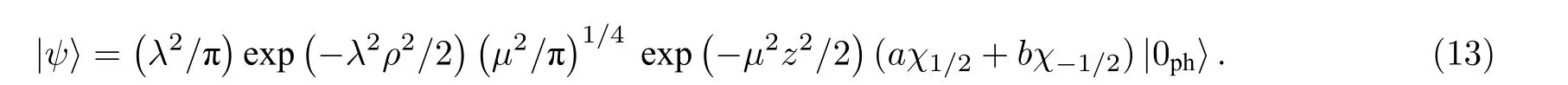
式中,aχ1/2+bχ1/2是z分量的两种自旋态,其中分别代表自旋向上和自旋向下态,a和b是系数.λ和µ是变分参量,|0ph是未微扰零声子态,作用于湮灭算符有bq|0ph〉=0,(12)式对 |ψ〉的期望值可以表示为

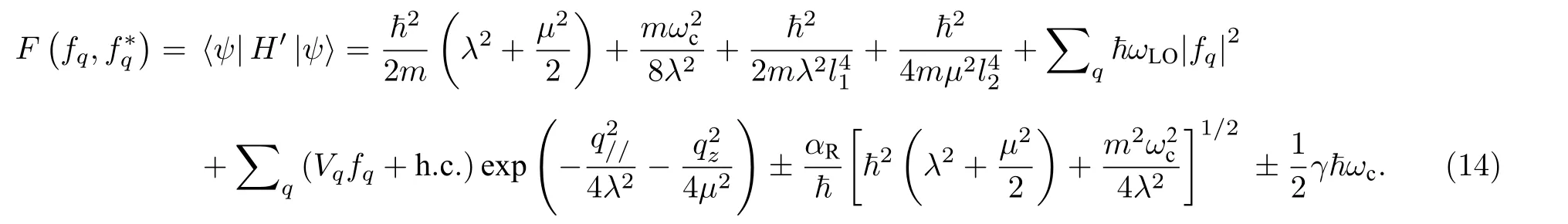
其中ωc=eB/(mc) 定义为磁场回旋共振频率,分别定义为横向和纵向有效受限长度,.

由变分法得到:

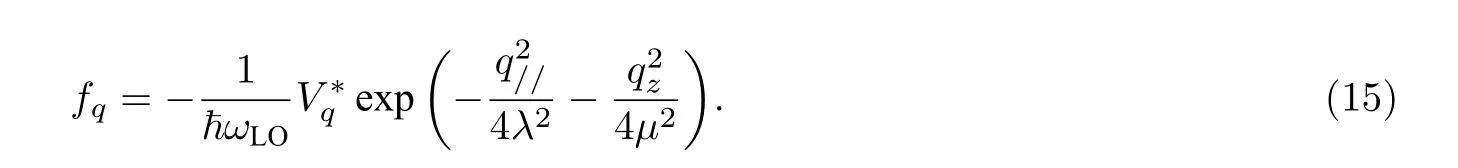
将(15)式代入(14)式中,求和变积分,得到系统的总能量:

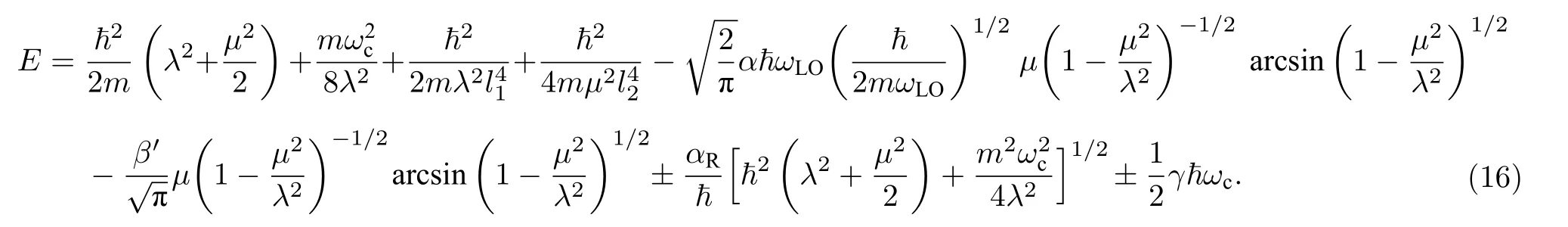
其中,束缚磁极化子的零自旋分裂能量为

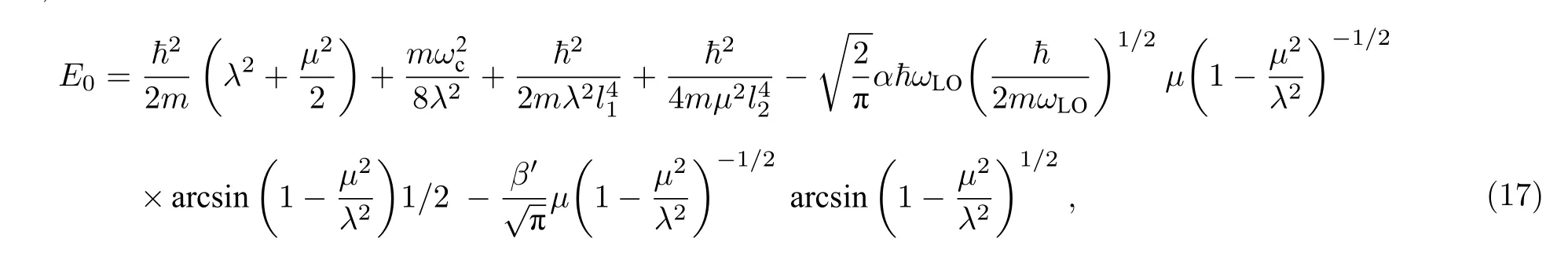
Rashba 效应影响下束缚磁极化子的能量为

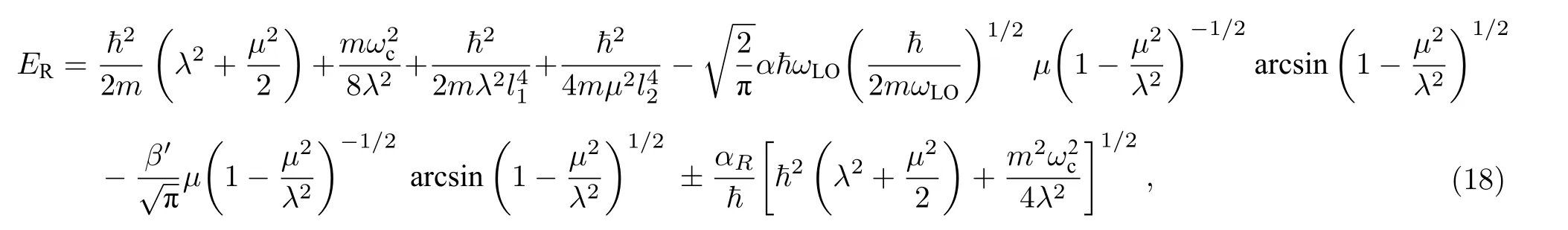
Zeeman 效应影响下束缚磁极化子的能量为

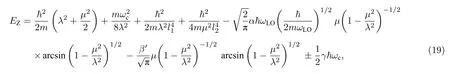
Rashba 自旋轨道分裂能为

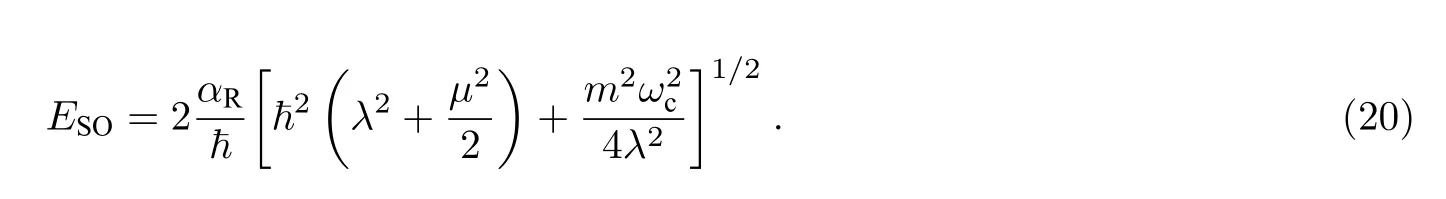
3 数值结果与讨论

为更清晰体现Rashba 效应和Zeeman 效应对各向异性量子点中束缚磁极化子性质的影响,数值计算了束缚磁极化子的基态能量.为简化计算,取极化子单位(ℏ=2m=ωLO=1),并使用wLO作为磁场回旋共振频率的单位.在不同库仑束缚势下讨论了束缚磁极化子基态能量与横向有效受限长度、纵向有效受限长度、磁场回旋共振频率之间的关系.在强、弱磁场下分别讨论了Zeeman 效应和Rashba 效应在分裂中所占的主导位置.

当ωc=1ωLO,l2=1.2,α=8,αR=1,β′=0,β′=20 时,图1 展示了束缚磁极化子基态能量E与横向有效受限长度l1之间的函数关系.当ωc=1ωLO,l1=0.6,α=8,αR=1,β′=0,β′=10时,图2 显示了束缚磁极化子基态能量E与纵向有效受限长度l2之间的函数关系.当ωc=10ωLO,l2=1.2,α=8,αR=1,β′=0,β′=20,图3 描绘了束缚磁极化子基态能量E与横向有效受限长度l1之间的关系曲线.当ωc=10ωLO,l1=0.6,α=8,αR=1,β′=0,β′=20,束缚磁极化子基态能量E对纵向有效约束长度l2的依赖关系如图4所示.从图1—图4 可以看出,束缚磁极化子的能量随着横向、纵向有效受限长度的减小而增大.这是因为随着约束长度的减小,电子的运动范围变窄,电子热运动能量和电子声子相互作用能增大.从图1—图4还可以看出,当l1和l2取值较小时,束缚磁极化子基态能量随着有效受限长度的减小迅速增加,说明量子约束效应取决于有效受限长度的取值范围,也就是说,有效受限长度越小量子约束效应越明显.

从图1—图4 可见,束缚磁极化子的基态能量分裂成几个分支,由于电子具有自旋磁矩和轨道磁矩,磁矩的方向和空间取向是量子化的,因此,能级在磁场下发生分裂,由磁场引起的能级分裂是Zeeman 分裂.半导体中电子自旋性质不仅与其自身磁矩有关,而且还与其轨道运动有关,如果晶体结构的反演对称性被破坏,即使没有外加磁场的影响,能量也会发生分裂.在窄禁带半导体中,Rashba自旋轨道分裂主要是由结构反演不对称引起的.此外,自旋-轨道耦合引起的Rashba 自旋轨道分裂在窄禁带半导体中更为明显.当磁场较弱时,从图1和图2 可以看出,Rashba 效应在分裂中占据主导地位.在强磁场下,从图3 和图4 可以看出,Zeeman效应在分裂中占据主导地位.

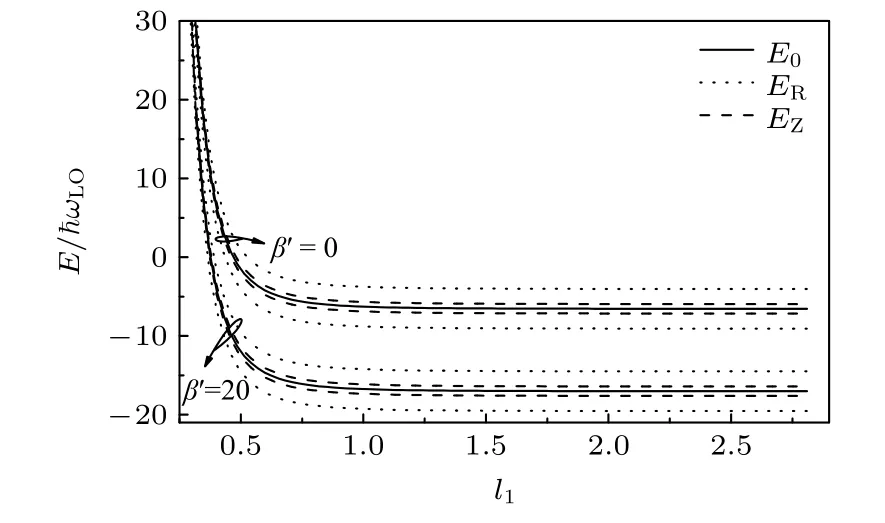
图1 取固定值ωc=1ωLO,l2=1.2,α=8,αR=1,当库仑束缚势β′ 取不同值时,束缚磁极化子基态能量E 与横向有效受限长度l1 之间的关系曲线Fig.1.For fixedωc=1ωLO,l2=1.2,α=8,αR=1,the relation of bound magnetopoloran ground state enegergy E with the transverse effectiveconfinement length l1 at different Coulomb bound potential β′.

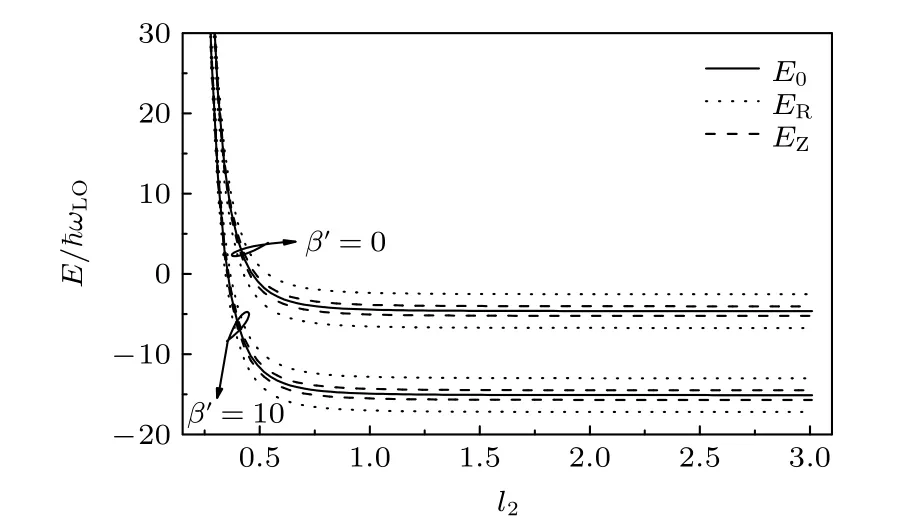
图2 取固定值ωc=1ωLO,l1=0.6,α=8,αR=1,当库仑束缚势β′ 取不同值时,束缚磁极化子基态能量E 与纵向有效受限长度l2 之间的关系曲线Fig.2.For fixedωc=1ωLO,l1=0.6,α=8,αR=1,the relation of bound magnetopoloran ground state enegergy E with the longitudinal effectiveconfinement length l2 at different Coulomb bound potential β′.

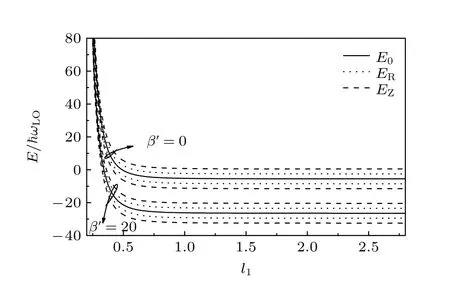
图3 取固定值ωc=10ωLO,l2=1.2,α=8,αR=1,当库仑束缚势β′取不同值时,束缚磁极化子基态能量E 与横向有效受限长度l1 之间的关系曲线Fig.3.For fixedωc=10ωLO,l2=1.2,α=8,αR=1,the relation of bound magnetopoloran ground state enegergy E with the transverse effective confinement length l1 at different Coulomb bound potential β′.

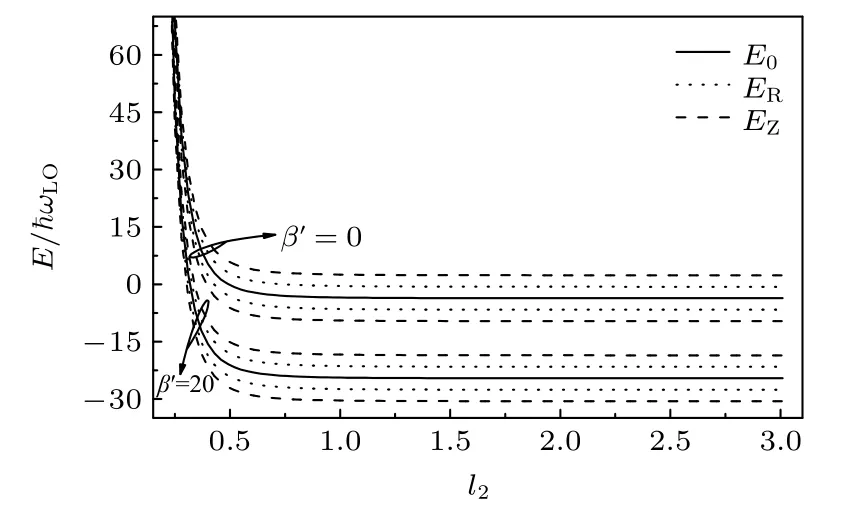
图4 取固定值ωc=10ωLO,l1=0.6,α=8,αR=1,当库仑束缚势β′ 取不同值时,束缚磁极化子基态能量E 与纵向有效受限长度l2 之间的关系曲线Fig.4.For fixedωc=10ωLO,l1=0.6,α=8,αR=1,the relation of bound magnetopoloran ground state enegergy E with the longitudinal effectiveconfinement length l2 at different Coulomb bound potential β′.

取固定值l1=0.4,l2=1.2,α=8,αR=0.5,β′=0,β′=20,图5 展示了束缚磁极化子基态能量与磁场回旋共振频率之间的函数关系.由图5 可见,当ωc=0 时,Zeeman 分裂是零.然而,在零磁场下,Rashba 自旋轨道分裂依然存在,这是由电子自旋轨道相互作用引起的电子零场自旋分裂.当磁场回旋共振频率取较小值时,Rashba 自旋轨道分裂比Zeeman 分裂更明显,且Rashba 效应在分裂中起主导作用.结果表明,随着磁场回旋共振频率的增加,Zeeman 分裂的能量间距增大,而Rashba自旋轨道分裂的能间距基本不变.这一结论表明,在强磁场作用下,Zeeman 效应占主导地位,Rashba效应可以忽略.

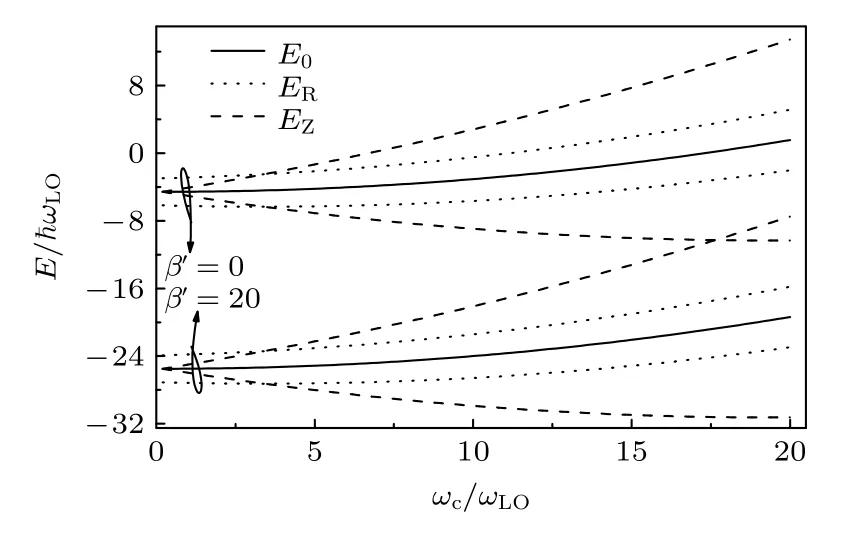
图5 取固定值l1=0.4,l2=0.8,α=8,αR=0.5,当库仑束缚势β′ 取不同值时,束缚磁极化子基态能量E 与磁场回旋共振评率ωc 之间的关系曲线Fig.5.For fixed l1=0.4,l2=0.8,α=8,αR=0.5,the relation of bound magnetopoloran ground state enegergy E with the magnetic field resonance cyclotron frequency ωc at different Coulomb bound potential β′.

在恒定磁场下,从图1—图4 还可以看出,Zeeman分裂能间距和Rashba 自旋轨道分裂能间距保持不变.在变化的磁场中,从图5 可以看出,Zeeman分裂的能间距变化较为显著,而Rashba 自旋轨道分裂的能间距随着磁场回旋共振频率的增大而缓慢增大,这是由于磁场对自旋轨道分裂的影响.从(16)式的第5 项可知,声子对极化子能量的贡献为负,声子的存在降低了粒子的总能量,所以极化子态比裸电子态稳定.

在图1 和图2 中,当l1取固定值时,库仑束缚β′势越大,对应的极化子能量越小.在图3 和图4中,当l2取固定值时,库仑束缚势β′越大,对应极化子能量越小.在图5 中,当磁场回旋共振频率ωc取固定值时,库仑束缚势β′越大,对应极化子能量越小.各向异性量子点中心存在类氢杂质,电子与类氢杂质之间存在库仑束缚势,由于库仑束缚势的存在,电子受到新的约束,使较大的电子波函数相互重叠,导致电子-声子相互作用增强.由(16)式可知,库仑束缚势对极化子的能量贡献为负值,库仑束缚势的存在降低了粒子的总能量,所以束缚极化子比裸电子态稳定.

图6 展示了当Rashba 参数αR取不同值时,Rashba 自旋-轨道分裂能ESO 随磁场回旋共振频率ωc的变化关系.由图可知,随着磁场回旋共振频率的增加,自旋轨道分裂能增大.当回旋共振频率ωc取定值时,Rashba 参数越大,自旋轨道分裂能越大,结果与文献[21]一致.由Rashba 自旋轨道分裂能的表达式(17d)知,Rashba 参量与自旋轨道分裂能成正比,当αR=0 时，电子自旋-轨道不发生分裂.

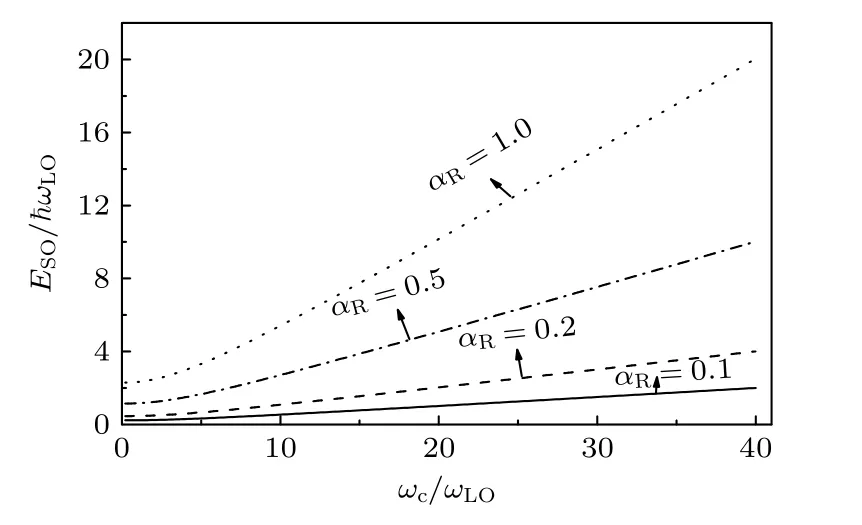
图6 Rashba 参 量αR 取不同值时,自 旋-轨道分裂能ESO 与磁场回旋共振频率ωc 之间的关系曲线Fig.6.Change of spin-orbit splitting energy ESO with the magnetic field resonance cyclotron frequencyωcat different Rashba parameter αR.

4 结论

采用Pekar 变分方法研究了各向异性量子点中束缚磁极化子的Rashba 效应和Zeeman 效应,通过理论推导,得到束缚磁极化子基态能量的表达式.分别讨论了束缚磁极化子基态能量与横向有效受限长度、纵向有效受限长度、磁场回旋共振频率及库仑束缚势的关系.在强、弱磁场下,对Rashba效应和Zeeman 效应对束缚磁极化子性质的影响做了比较.当有效受限长度取值较小时,束缚磁极化子的能量随有效受限长度的减小而迅速增加,体现了新奇的量子约束效应.弱磁场下,Rashba 效应在能量分裂中占主导位置;强磁场下,Zeeman 效应在能量分裂中占主导位置.库仑束缚势和声子对极化子的能量贡献都为负,杂质和声子的存在降低了极化子的总能量,所以束缚极化子比裸电子态更稳定,能量分裂较裸电子也相对稳定.