基于PSO-ELM的液压油性能衰退预测及分析*

宋新成 杨 洁 王 崴 李恒威 郝俊杰 郭亮亮

(1.空军工程大学防空反导学院 陕西西安 710051；2.解放军93285部队 吉林公主岭 136100)

在大功率武器装备伺服驱动系统中，液压系统发挥着巨大作用，对提升我国国防实力起到了重要作用。与此同时，当其一旦发生故障，将直接影响整个装备的正常作业，进而延误战机。研究人员从装备可靠性角度出发，分析历年来装备液压系统故障案例，发现75%以上的故障根源可追溯为液压油的性能衰退。液压油的性能衰退会加速液压泵、液压阀等元件的过早磨损，甚至导致卡死、堵塞等故障。因此，在战场环境载荷下，通过预测液压油的性能衰退情况，及时确定换油时机，对武器装备的健康管理具有重要意义[1]。

通过预测液压油的性能衰退情况，及时确定换油时机，对于保证装备正常使用效能和延长寿命十分重要[2]。由于单一指标很难准确反映液压油的质量，众多学者在数学分析的基础上，提出了一些评价的模型和综合性指标，实现了对液压油综合性能衰退情况的预测。WANG等[3]运用模糊综合评价方法，对液压油性能进行了综合评价，但模糊推理的权值系数确定主观性太大。虞文胜[4]采用改进的BP神经网络对抗磨液压油进行软测量，但该方法对小样本的预测效果不佳。刘金平和杨勇辉[5]运用模糊聚类理论，对液压油质量进行了分类，细化了液压油质量评判尺度，但该方法在大样本量情况下，聚类结论获取比较困难。程安国等[6]采用层次分析法，建立了综合评价模型，但该模型只给出指标重要性程度，未进行液压油综合性能评价。

上述文献提出的液压油综合性能预测方法不同程度存在不足，在实际的预测中，大多采取多种预测方法融合的方式[7-9]，从而取得了更为准确的预测效果。因此，本文作者提出基于粒子群优化(Particle Swarm Optimization，PSO)的极限学习机(Extreme Learning Machine，ELM)的液压油性能衰退预测方法，以LHM-46抗磨液压油为例，实现了液压油的性能衰退预测。ELM是一种新型的快速学习算法，具有运算速度快、学习过程易于在全局极小值收敛、泛化性能好等优点[10]。但由于ELM算法的初始输入层权值Wi和隐含层偏差bi是否合理直接影响预测结果，因此文中采取PSO对其参数进行优化[11]，同时采用遍历选取法[12]优化嵌入维数m和隐含层节点个数L，从而建立了最优的性能衰退预测模型。

1 ELM极限学习机

ELM是一种计算简单、训练速度快速的单隐层前馈神经网络(SLFN)，可以初始化输入层权值和偏置并得到相应的输出权值[13]。

如图1所示，对于一个SLFN网络，假设有N个任意的样本(Xi,ti)，其中

图1 SLFN结构Fig 1 SLFN structure

Xi=[xi1,xi2,…,xin]T∈Rn

(1)

ti=[ti1,ti2,…,tim]T∈Rm

(2)

对于一个有L个隐层节点的单隐层神经网络可以表示为

(j=1，…,N)

(3)

式中：Wi=[wi1,wi2,…,win]T为输入层权值;g(x)为激活函数；βi为输出权值。

单隐层神经网络学习的目标是使得输出的误差最小，可以表示为

(4)

即存在βi、Wi和bi，使得

(j=1，…，N)

(5)

可以矩阵表示为

Hβ=T

(6)

式中：H是隐层节点的输出；β为输出权值；T为期望输出。

(7)

(8)

(9)

(10)

训练单隐层神经网络可以转化为求解一个线性系统Hβ=T。并且输出权值β可以被确定

(11)

其中，H+是矩阵的Moore-Penrose广义逆,且可证明求得的解的范数是最小的并且唯一[14]。

2 基于PSO-ELM的液压油性能衰退预测

2.1 外部参数优化

在液压油的性能衰退进程中，不同阶段的性能衰退指标均构成一个一维向量，但ELM算法输入量是多维向量，因此采用相空间重构算法将一维指标向量转化为ELM的m维输入向量。

对于式(1)中的输入Xi,i=1,…,n

构造Yi=(Yi,Yi-τ,…,Yi+(m-1)τ)

其中，1≤i≤n-(m-1)τ，m为嵌入维数，τ为延迟时间。

嵌入维数m对预测精度有直接影响，m过大会导致数据庞大，训练时间过长，过小又会导致预测不准确[15]。L的选取也存在取值过小精度低、过大训练速度慢的特点。

而一般ELM的节点个数选择经验公式(12)主观性偏大，结果可信度偏低。

(12)

式中：n为输入层节点个数；a为1～10之间的常数。

因此利用遍历选取法同时确定相空间重构嵌入维数m及隐含层节点个数L，确定m的遍历区间为[1,6]，确定隐含层节点个数L的遍历区间为[1,21]。在遍历区间内穷尽所有组合，以预测精度最小为目标，进行遍历搜索。

2.2 内部参数优化

由式(3)、(7)可以看出，初始输入层权值Wi和隐含层偏差bi取值对输出权值矩阵有直接影响，因此以预测精度为标准，利用PSO对Wi和bi进行优化。具体如下：

确定种群长度D=L(m+1)，其中θw为种群中的第w(1≤w≤W)个粒子。将输入层权值Wi和隐层的偏置bi作为粒子(Wi，bi)。

产生种群

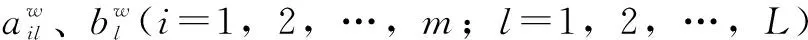
利用ELM训练集得出每个粒子的均方根误差(RMSE)ε。RMSE即为粒子群优化算法的适应度函数。

(13)

2.3 算法预测流程

整体模型预测流程如图2所示。具体步骤如下：

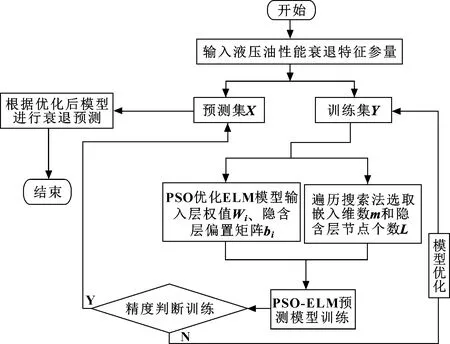
图2 PSO-ELM液压油预测流程Fig 2 Flow of PSO-ELM hydraulic oil prediction

STEP1 输入液压油样本性能衰退特征参量数据，划分预测集和训练集；

STEP2 将训练集分别输入PSO和遍历搜索进行优化选取ELM参数;

STEP3 运用PSO对ELM算法的输入层权值Wi和隐含层偏差bi进行优化选取，同时采取遍历搜索对嵌入维数m和隐含层节点数L进行优化；

STEP4 将优化后参数输入PSO-ELM算法进行训练迭代；

SREP5 对迭代结果进行精度判断训练，若满足精度要求，则进行STEP6，反之，返回STEP2；

STEP6 将预测集输入优化后的PSO-ELM算法进行衰退预测；

STEP7 输出预测结果，程序结束。

3 液压油性能衰退实验

液压油性能衰退的衡量指标众多，而在实际的野战环境下，很难携带过多精密的检测设备和仪器，如颗粒检测仪、红外光谱仪等对油液指标进行精确测量。而黏度、张角、含水量可通过一些便携式的仪器，如THY-21C油液检测仪和NDJ-5S数字黏度计等进行检测，符合实际的训练和作战需求。并且黏度和含水量作为液压油质量的主要指标，通过其变化也能反映油液的衰退情况。

3.1 实验流程

以LHM-46抗磨液压油为例，利用THY-21C便携式油液质量检测仪测量油液样本的含水量和衰退度，利用NDJ-5S数字黏度计测量油液样本的黏度和张角。实验流程如图3所示。

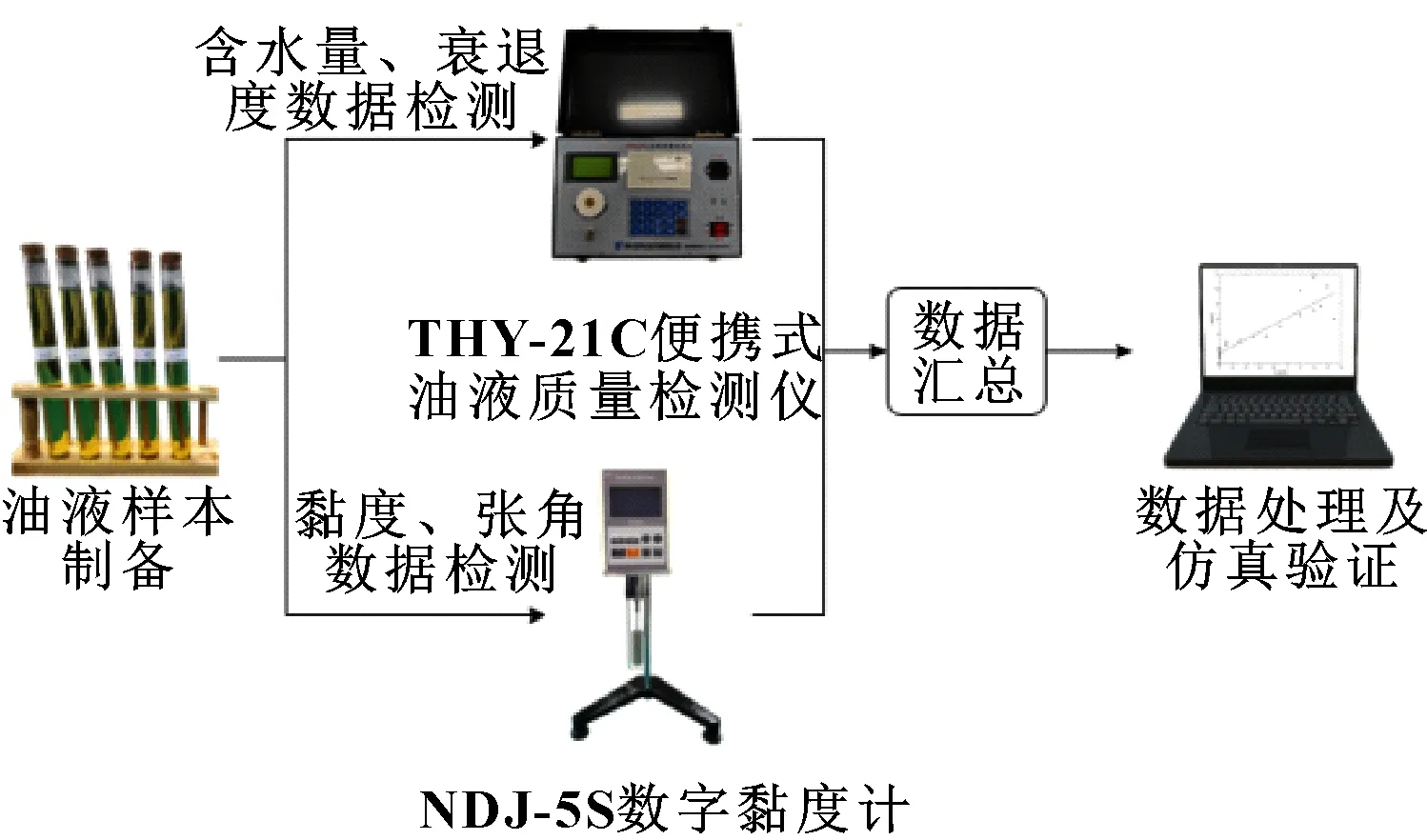
图3 实验流程Fig 3 Experimental flow

3.2 样本获取

在液压装备的实际运行中，无法对液压油频繁抽取及检测，数据采集比较困难。在液压系统运行过程中，液压油的污染主要来自系统内部和空气中的颗粒物，并且以系统内部运行产生的颗粒物居多。因此，可以通过将新油和废油以不同比例混合，来模拟液压油性能衰退的不同阶段，同时避免实验过程中其他污染源对结果产生的干扰。

以废油占比0～100%为整体样本容量，每5%作为一个样本，得到21组油液衰退模拟样本。

通过对油液衰退模拟样本的检测，测得不同污染度下油液的黏度、张角、含水量如表1所示。

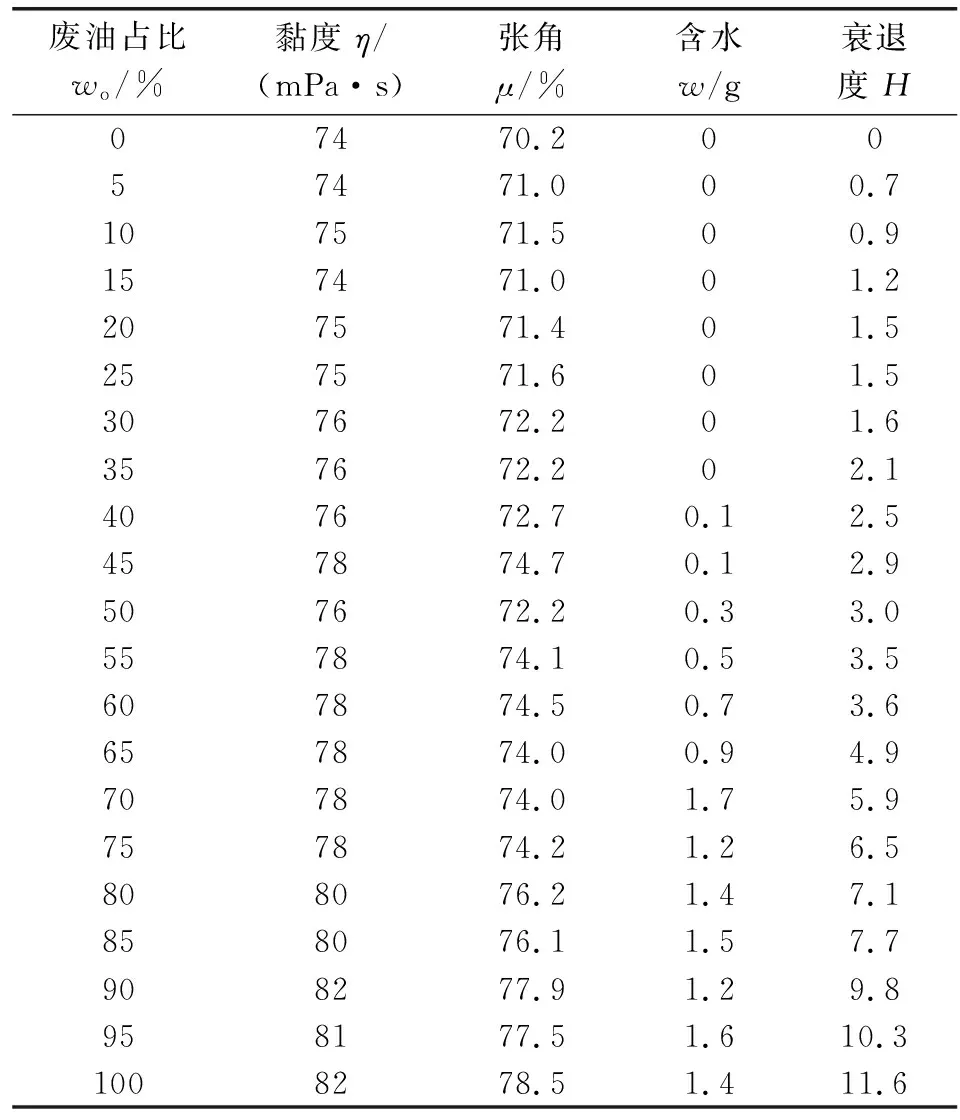
表1 油液衰退模拟样本检测数据Table 1 Test data of simulated oil decay samples

4 数据分析及仿真

4.1 衰退度变化分析

以黏度η、张角μ、水分含量w为三维坐标，以球体直径表征衰退度大小，作四维可视化分析如图4所示。

图4 衰退度变化四维分析Fig 4 Four dimensional analysis of decline degree change

由图4可观察到随着黏度、张角和含水量的增加，油液性能不断衰退。随着设备运行次数增加，油液内的抗氧化剂逐渐消耗，使得油液氧化程度增加，引起酸值增长，进而会加速固体颗粒度升高，进而加速了黏度的增加。固体颗粒度的增加不仅加剧污染，还会带来磨损失效甚至突发失效；黏度的增加使得元件摩擦和发热，动作灵敏度下降，系统压力损失增大。另外，可以看到含水量在衰退进程中变化并不大，对衰退度影响权重也较小。在衰退度达到6，即废油占比70%左右，根据THY-21C仪器使用说明，该油品性能指标已经超出正常范围，需要进行油品的更换了。

4.2 多元回归分析

对液压油的黏度、张角、含水量与衰退度进行多元回归分析，判定LHM-46抗磨液压油衰退度H与黏度η、张角μ、水分含量w的相关性关系，建立初步模型。

(1)用衰退度H与黏度η、张角μ、水分含量w作回归，得：

(2)计算衰退度H与黏度η、张角μ、水分含量w之间的复决定系数R2。

(14)

(3)求得R2=0.952 576>0.8，根据卡尔·皮尔逊相关系数定义，认为衰退度H与黏度η、张角μ、水分含量w存在强相关性关系。

(4)求得系数矩阵，代入得出

H=-64.454-0.279η+120.949μ+1.909w

(5)计算预测误差

(15)

求得εp=0.534 29

显然，由于该模型为基于黏度η、张角μ、水分含量w得出的线性化模型，预测准确度只有46.57%。需要采取算法进行拟合和验证。

4.3 仿真验证

在收集到的21组实验数据中，随机选择6组样本构成模型的预测集X，剩余的15组构成训练PSO-ELM算法的训练集Y。

模型建立并调试后，通过计算机对预测结果及准确率进行验证。

仿真验证如图5所示，根据式(14)(15)计算，结果显示：优化的PSO-ELM算法对LHM-46抗磨液压油的预测误差εp=0.015 296，复决定系数R2=0.928 5，ELM的预测误差εp=0.130 08，复决定系数R2=0.409 64。

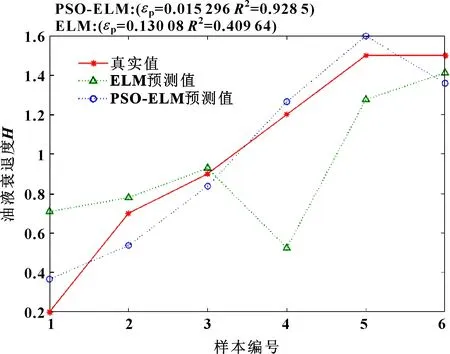
图5 PSO-ELM、ELM性能衰退预测结果与实验结果比较Fig 5 Comparison of performance degradation prediction results of PSO-ELM and ELM with experimental results

PSO-ELM的衰退预测模型准确率达到了98.47%，与ELM算法只有87.00%的预测精度对比，该模型预测准确率更高；并且其复确定系数相比而言更趋近于1，预测相关性也更高，更为符合实际的实验衰退度。总的来说，基于PSO-ELM衰退预测模型的方法在液压油的性能衰退预测领域有较高参考价值。

5 结论

(1)提出基于粒子群优化(Particle Swarm Optimization，PSO)的极限学习机(Extreme Learning Machine，ELM)的液压油性能衰退预测方法。经过PSO和遍历搜索优化的ELM算法预测准确度高，相对于普通的ELM算法有更好的预测效果，为研究液压油的性能衰退提供了一种更为有效的预测模型。

(2)通过将新油和废油以不同比例混合，以不同废油占比的方式模拟实际的液压油运行中的衰退情况，能相对准确快速地实现油液衰退的加速实验，数据的采集更方便快捷。

(3)选取液压油的黏度、含水量和张角指标来预测油液衰退情况有良好的预测效果，在此基础上可继续增加指标维度，进一步提升预测效果。

(4)PSO-ELM算法对于大样本量的液压油预测准确度可以更高，下一步可以继续在丰富样本来源和数据的基础上继续训练，提高预测精度。