基于确定性规则的机电飞轮电动汽车控制策略
2022-01-19魏书斌孙宾宾李波张锡
魏书斌,孙宾宾,李波,张锡
(山东理工大学 交通与车辆工程学院, 山东 淄博 255049)
当今世界,环境污染和能源短缺等问题日益严重,发展新能源汽车已成为各国节能减排的重要措施,其中,纯电动汽车由于续航里程短等原因限制了发展。飞轮具有功率密度大、能量转换快、能量转换效率高等优点[1],因此可以将飞轮应用到汽车上,制动时将动能储存在飞轮中,加速时将飞轮动能释放,达到增强动力和降低能耗的效果。文献[2]将飞轮储能系统应用到电气化铁路牵引供电系统进行削峰填谷,以达到降低牵引变压器的峰值功率,提高牵引供电系统电能质量的效果。
控制策略的优劣直接影响汽车的动力性、经济性和驾驶性,所以控制策略是动力系统的研究重点。文献[3]针对某功率分流式混合动力汽车,提出一种基于粒子群优化的多目标控制策略,实现降低能耗和控制电池电量的双重目标。
本文的研究对象为机电飞轮电动汽车(electromechanical flywheel electric vehicles, EFEV),在单一锂电池储能系统的基础上引入机电飞轮系统,将飞轮功率密度高和锂电池能量密度高的特点相结合,提出机电飞轮复合储能系统。这在节能方面具有显著优势,但多种工作模式也为能量管理带来了挑战。为了在保证动力性的基础上提高经济性,本文提出基于确定性规则的控制策略。
1 机电飞轮系统
以国内某MPV为原型车,在保证车辆动力性的前提下[4],将其改装为机电飞轮电动汽车。如图1所示,该机电飞轮电动汽车的前轮由主驱电机驱动,后轮由机电飞轮系统直接驱动。
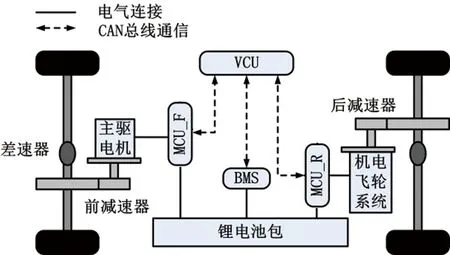
图1 机电飞轮电动汽车构型示意图
机电飞轮系统是一种集成飞轮、调速电机、行星齿轮机构及离合器的混合动力系统。如图2所示,调速电机直接连接太阳轮,飞轮通过一对减速齿轮、离合器与齿圈连接,行星架则连接变速机构输出动力至车轮。

图2 机电飞轮系统结构
由于飞轮功率密度很大,因此将其作为辅助动力源,利用飞轮瞬时大功率输入或输出的优势,一方面,在满足整车动力性的前提下,可以匹配功率更小的主驱电机,提高车辆在中低负荷工况下系统工作效率[5-8];另一方面,可以避免负载突变工况下电池会大电流充放电,进而提高能源系统工作效率并延长其使用寿命。机电飞轮系统工作模式见表1。

表1 机电飞轮系统工作模式
2 控制策略
综合考虑整车特点,结合行驶工况,本文提出基于确定性规则的控制策略,输入参数为车速v、加速度a、车辆需求转矩Tdmd、电池荷电状态SC、飞轮能量状态SE,目的是保证主驱电机、调速电机和飞轮都可以运行在安全、高效的区域。Tin为机电飞轮系统介入转矩;SCh,SCl分别为电池荷电状态的上下界限;SEh,SEl分别为飞轮状态的上下界限。
1)在起步工况下,(v<10 km/h)∩(a>0)且SC>SCl时,具体策略如下:
当Tdmd
2)在加速工况下,(v>10 km/h)∩(a>0)且SC>SCl时,具体策略如下:
当Tdmd 3)在减速工况下,a<0∩SC a)当SE b)当SE≥SEh时,同样会出现以上4种情况,但离合器分离,而飞轮不参与制动,回收制动能量的部件只有主驱电机和调速电机。 4)在驻车工况下,v=0∩SC 当SE>0时,调速电机回收飞轮剩余能量;当SE<0时,飞轮没有剩余能量可回收。 为保证仿真顺利进行[9],采用MATLAB/Simulink建立了基于确定性规则控制策略的整车仿真模型,其能源动力系统模型如图3所示。 图3 能源动力系统模型 机电飞轮电动汽车采用机电飞轮复合储能系统方案,其相关参数和动力性指标见表2和表3。原型车采用单电机直驱方案,其相关参数见表4。 机电飞轮电动汽车在行驶过程中,受到滚动阻力、空气阻力等外力作用,其动力学方程可描述为 (1) 式中:Ft为驱动力;Ff为滚动阻力;Fi为坡度阻力;Fw为空气阻力;Fj为加速阻力;Tt为作用于驱动轮上的转矩;r为车轮半径;m为整车质量;g为重力加速度;f为滚动阻力系数;α为道路坡度角;CD为空气阻力系数;A为迎风面积;ua为车速;δ为汽车旋转质量换算系数;du/dt为行驶加速度。 表3 机电飞轮电动汽车动力性指标 表4 单电机直驱方案相关参数 电机模型主要依据电池状态参数及控制信号,计算并输出电机驱动、制动转矩[10-11],即 (2) 式中:Cd为无量纲转矩控制信号参数,取值范围为[-1,1],Cd大于0表示电机工作于电动状态,Cd小于0表示电机工作于发电状态;J为电机转动惯量;dω/dt为电机角加速度;Tc_tem_max为基于电机温度的峰值转矩修正值。 根据工作状态的不同,电机功率Pmc可以表示为 (3) 式中:Tmc为电机转矩;nmc为电机转速;ηmc为电机效率。 电机效率ηmc与电机转矩和转速有关,计算公式为 ηmc=fTmc,nmc, (4) 根据式(4),可以得到电机效率MAP,如图4所示。 (a) 主驱电机 飞轮模型采用飞轮能量状态SE的概念来类比化学电池的荷电状态以研究飞轮的能量特性,计算公式为 (5) 式中:nfw为当前飞轮的转速;nfw_max为飞轮最大工作转速。 飞轮储存的总动能E与转速有关,即 (6) 式中:ω为飞轮的转速;J为飞轮的转动惯量,由其形状、质量分布及转轴位置决定,计算公式为 (7) 式中:mi为飞轮上某质点的质量;ri为质点和转轴的垂直距离。 行星齿轮机构模型主要用于耦合转速,已知太阳轮、齿圈、行星架分别与调速电机、飞轮、车轮直接或间接相连接。调速电机、飞轮与车轮的转速关系为[12] (8) 式中:nwheel、nsrm、nfw分别为车轮、调速电机和飞轮的转速;k为行星排特征参数;ifd为行星架至车轮的传动比;ifw-r为飞轮至齿圈的传动比。 忽略在稳定运行状态下的能量损耗[13-15],则作用在调速电机、飞轮和车轮的转矩关系式为 Twheel=-ifd1+kTsrm=-1+k/kifw-rTfw, (9) 式中Twheel、Tsrm、Tfw分别为车轮、调速电机和飞轮的转矩。 电池模型主要用于估算电池荷电状态,其计算公式为 (10) 式中:SOC0为电池荷电状态初始值;Ib为电池电流;Ce_t_max为给定温度下电池最大容量。 电池功率可以表示为 (11) 式中:Pb为电池功率;Eb为电池开路电压;Ib为电池电流;Rb为电池内阻。 为了验证控制策略的动力性,建立机电飞轮电动汽车模型并进行仿真,仿真结果见表5,结果表明机电飞轮电动汽车能够满足动力性要求。 表5 动力性仿真结果 机电飞轮电动汽车仿真模型以NEDC工况为研究工况,对比车速跟随情况、电池SOC、电机高效区间工况占比、电机驱动效率,从而进行经济性验证[16]。如图5所示,所构建的整车模型能够以较高的精度跟随NEDC循环工况车速标准值,表明了仿真模型及控制策略的有效性。由图6可知,在NEDC工况下,机电飞轮电动汽车的SOC下降幅度较小,耗电量减少了0.89%,结果表明,相较于单电机电动汽车,采用确定性规则控制策略的机电飞轮电动汽车在经济性方面表现更佳。 图5 NEDC工况下EFEV仿真结果 图6 NEDC工况电池SOC变化曲线 从图7—图9可以看出,在驱动阶段,主驱电机、调速电机和飞轮能够满足整车驱动需求转矩;在制动阶段,除以上三者外,还需借助前后轮进行机械制动,满足制动需求转矩。仿真结果表明整车模型能够依据控制策略实现合理的转矩分配,满足整车行驶需求。 图7 NEDC工况需求转矩曲线 图8 电机及飞轮转矩曲线 图9 前后轮制动转矩曲线 如图10所示,在NEDC工况下,单电机直驱方案受单级变速拓扑结构的限制,单电机在某时刻不可避免地运行于低效工况域A内(中低车速、高负荷工况),整车驱动能效偏低;而机电飞轮复合储能方案,通过控制策略控制,可实现主驱电机驱动效率优化(将原低效工况域A内单电机工况点优化到主驱电机的高效工况域B内),改善整车驱动能效。 (a) 单电机直驱 如图11所示,NEDC工况下,相比单电机直驱方案,主驱电机的平均驱动效率提升了8.3%,调速电机的提升了3.2%。结果表明,机电飞轮复合储能方案借助系统拓扑结构优势,在电机驱动效率方面优于单电机直驱方案。 (a) 主驱电机与单电机效率对比图 如图12所示,对于单电机直驱方案而言,由于匹配的电机峰值转矩偏大,会造成电机高效区间偏离高频低负荷工况的问题。而调速电机驱动模式能够显著提升高频低负荷工况与其高效区间的匹配度,避免出现“大马拉小车”现象。 图12 调速电机驱动模式工况特征规律 如表6所示,NEDC工况下,与单电机直驱方案相比,机电飞轮复合储能系统运行于高效工况(效率>90%)的比例提升了19.9%,而工作于低效工况(效率<80%)的比例降低了13%,循环工况平均驱动效率提高了8.2%。从电机效率分布规律分析,机电飞轮复合储能方案优于单电机直驱方案,经济性能更佳。 表6 NEDC工况下不同方案电机效率分布规律 本文以机电飞轮电动汽车为研究对象,采用基于确定性规则的控制策略,建立机电飞轮电动汽车模型并进行仿真,通过对比仿真结果,得到以下结论: 1) 该机电飞轮电动汽车按照本文提出的控制策略能够满足动力性要求,实现合理的转矩分配,满足实际转矩需求。 2) 与单电机直驱方案相比,机电飞轮复合储能方案能够显著提升循环工况与电机高效区间的匹配度,有效提高系统驱动效率,降低耗电量。 3) 通过仿真证明,本文制定的控制策略能够保证机电飞轮电动汽车在满足动力性的基础上提高经济性。3 仿真建模
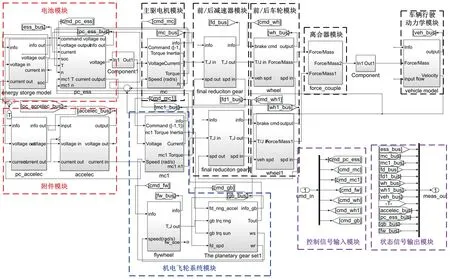
3.1 车辆纵向动力学模型


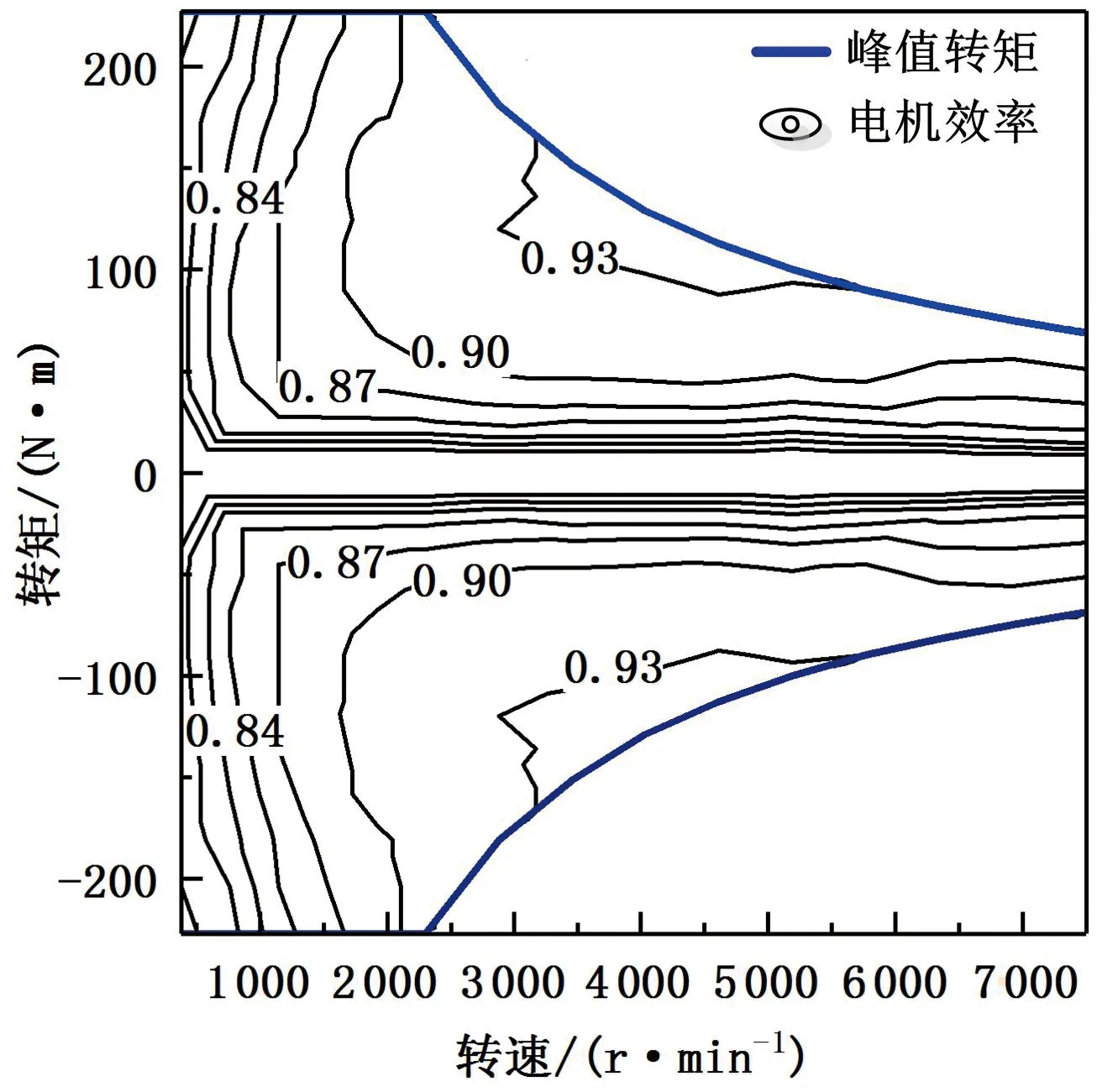
3.2 电机模型
3.3 飞轮模型
3.4 行星齿轮机构模型
3.5 电池模型
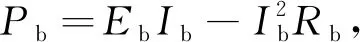
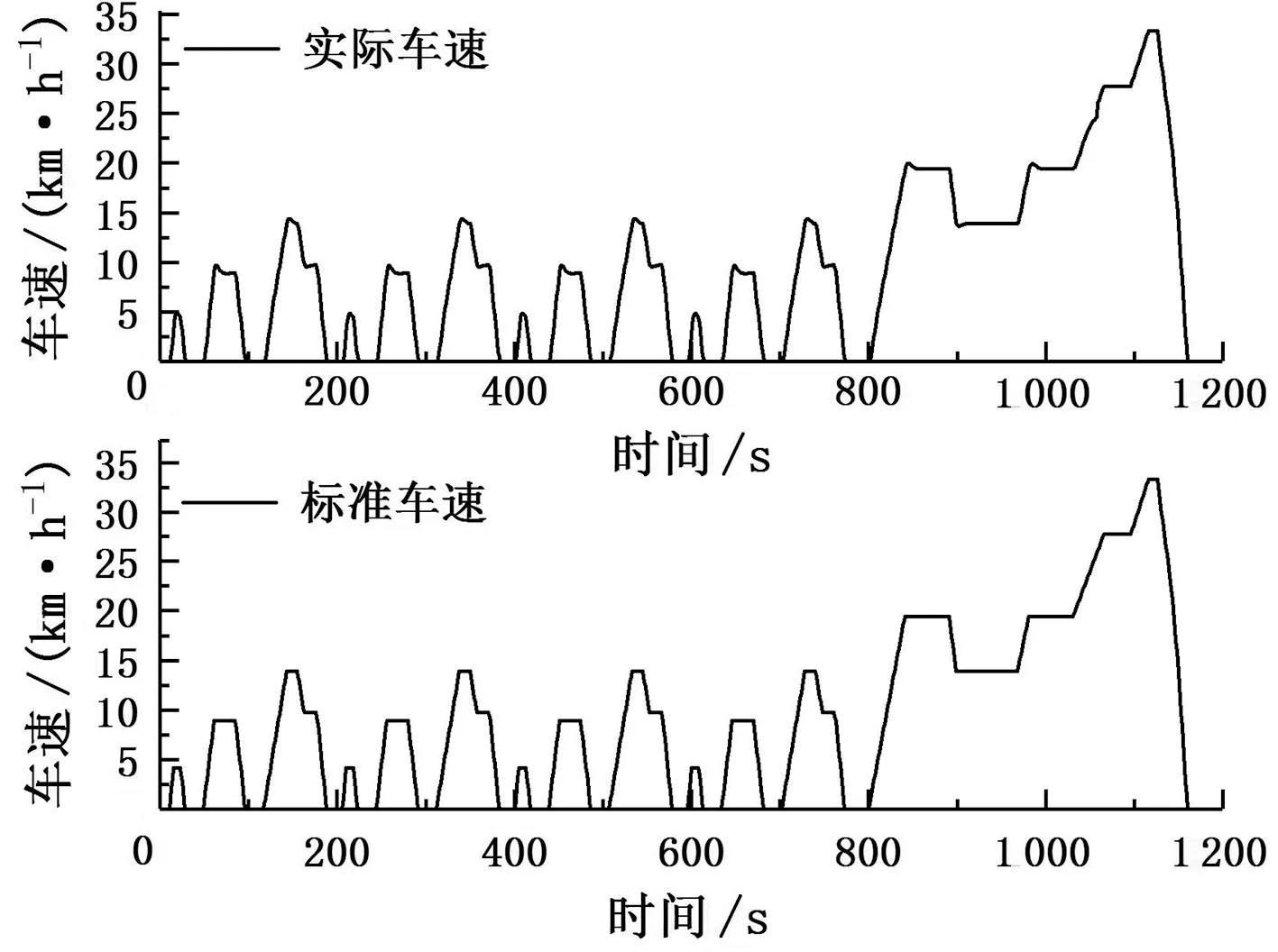
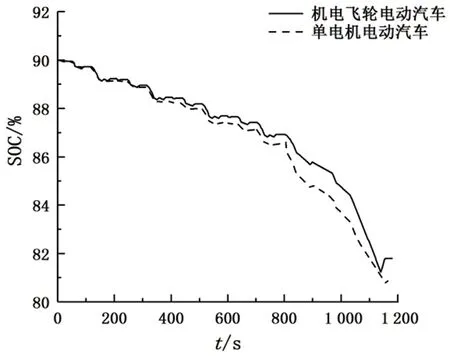
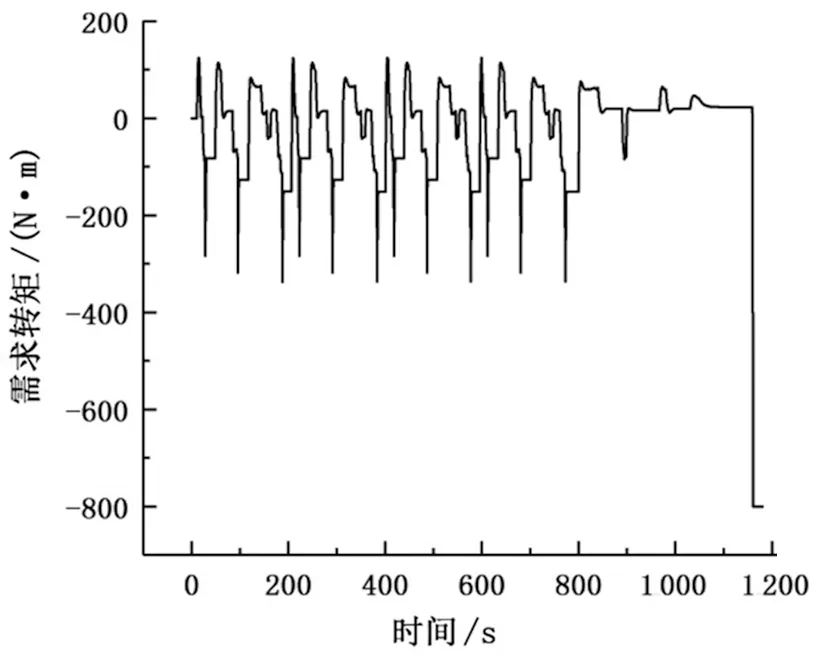
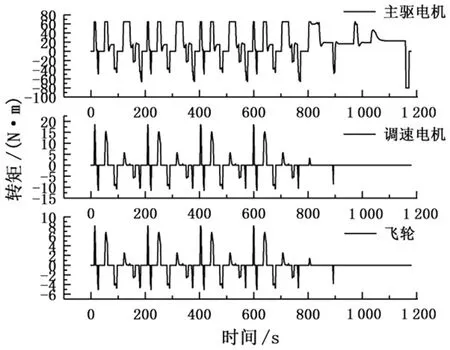
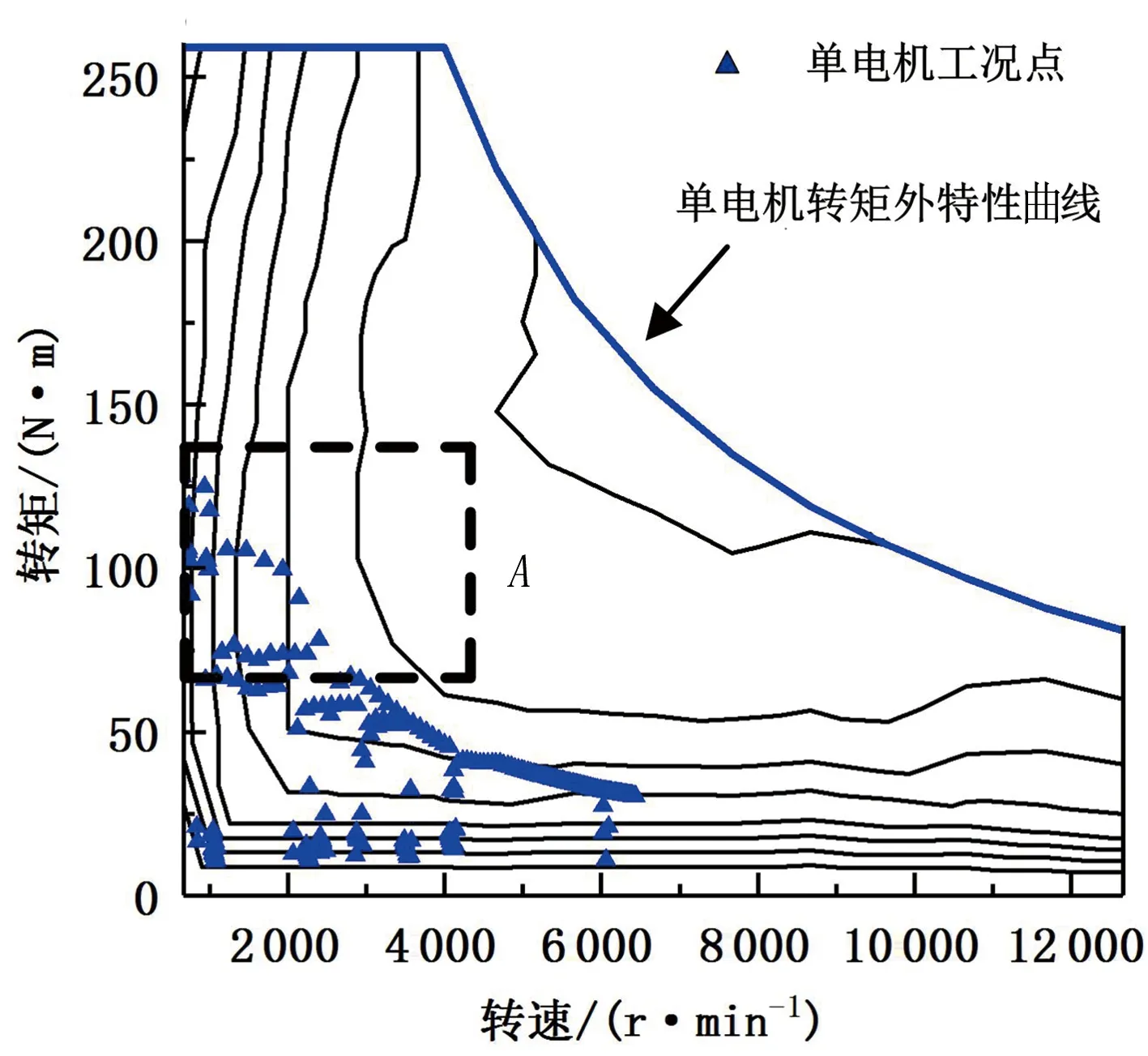
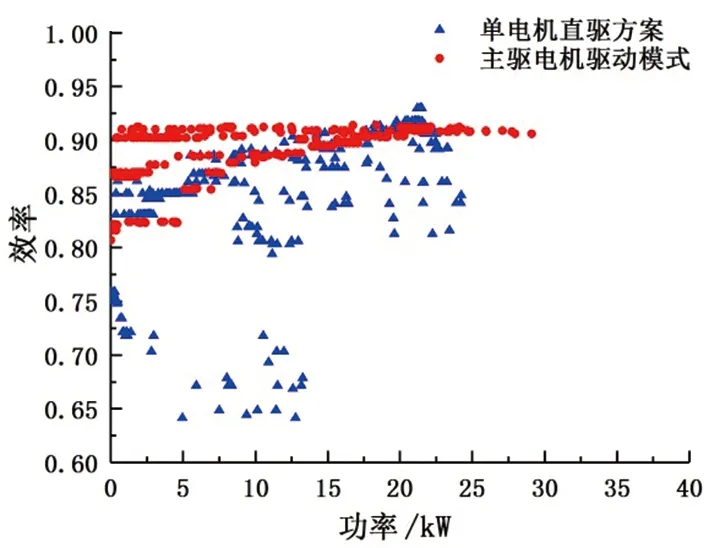
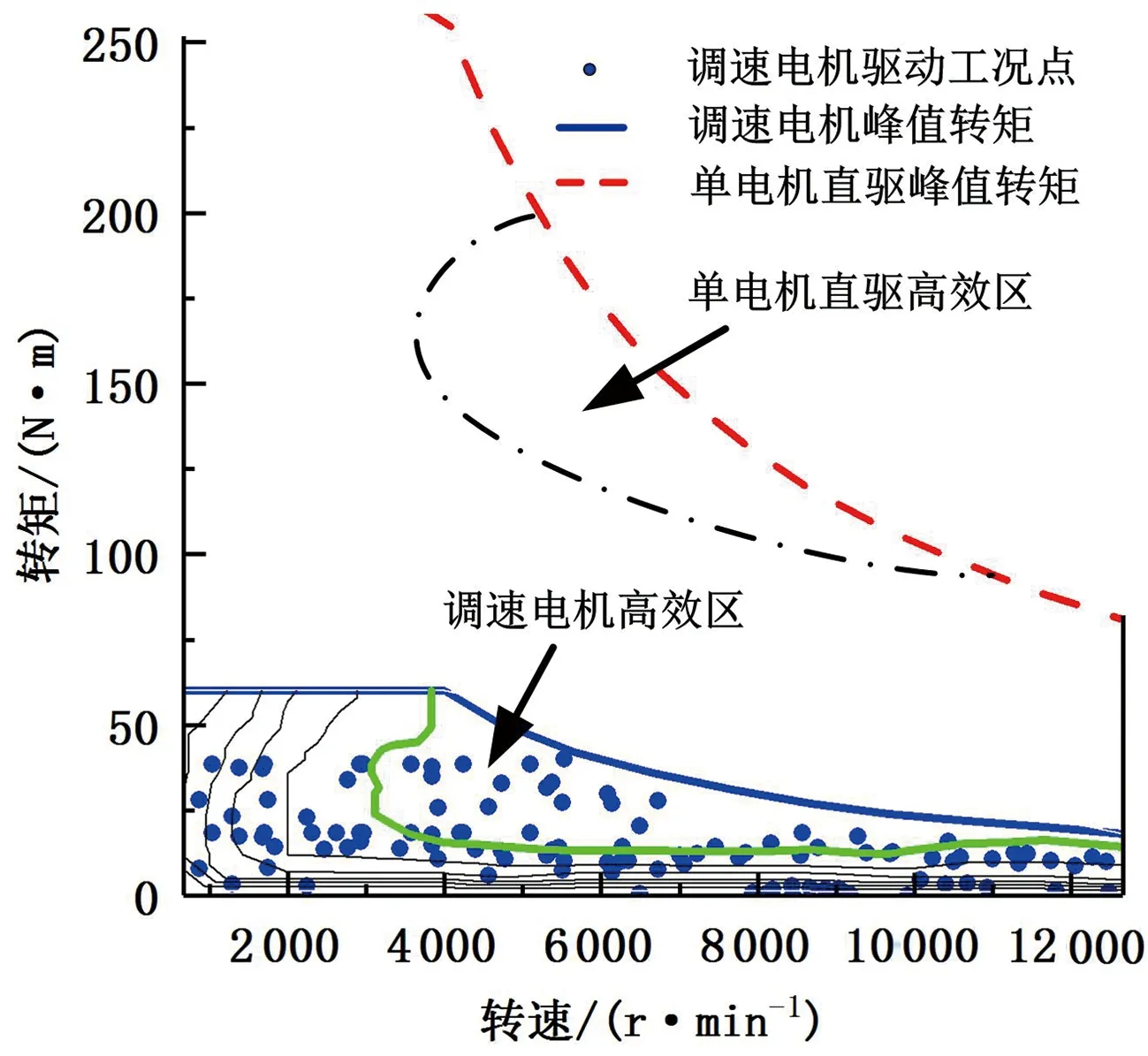
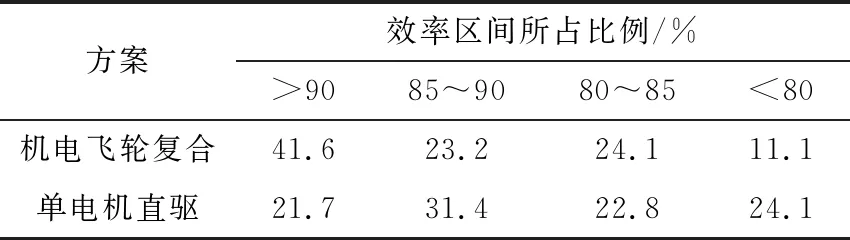
4 仿真分析


5 结论
