平衡损失函数下具有两水平共同效应的信度模型
2022-01-19王思敏李岩纪彩玲买淑萍
王思敏,李岩,纪彩玲,买淑萍
(宁夏大学 数学统计学院,宁夏 银川 750021)
信度理论是进行经验保费厘定的一个重要方法,在非寿险精算中占有重要的地位并得到了广泛的应用。自Bühlmann[1]从贝叶斯的观点出发,通过假设风险之间相互独立且历史索赔在给定风险下为独立同分布,在平方误差损失最小下建立了无分布限制的经典信度模型以来,学者对信度理论展开了研究。关于信度理论的详细介绍,具体可见文献[2]。然而,在实务中,风险不一定是相互独立的,可能存在某种相依关系。事实上,人们已经认识到,在许多重要的保险情景中,此类独立性的假设与实际是相违背的。例如,在恶劣的天气条件下,一辆汽车的碰撞会引发多辆汽车相继碰撞,从而导致多次索赔;同一楼层的住户会面临共同的火灾或地震风险等。目前,学者已关注到这一问题,并研究了具有相依结构的信度模型。如Yeo等[3]首次提出用共同效应(随机潜在风险参数)来刻画风险间的相依性,研究了正态分布下的信度保费估计;Wen等[4]研究了具有共同效应的Bühlmann和Bühlmann-straub模型,得到了无分布形式的信度估计;Wen[5]假设风险间存在相关性,研究了具有等相关的信度估计;郑丹等[6]研究了风险内部具有相依结构的信度模型;Poon等[7]考虑了空间条件相依和风险相依的信度模型,并给出了结构参数的估计。
以上研究均以平方损失函数为基础,所得结果称为纯保费。但在保险实务中,纯保费不可能被保险公司收取,而且利用平方损失函数得到的保费估计在有些情况下并不精确。已有学者注意到由保费估计过高或过低引起的损失并不相同,他们采用平衡损失函数对保费和风险的合适程度进行刻画,并取得了丰富的成果,如黄维忠[8]研究了平衡损失函数下具有风险相依结构的回归信度模型;Zhang等[9]进一步在平衡损失函数下讨论了带有利率且风险和时间相依的信度估计;李新鹏等[10]则研究了平衡损失函数下更一般的风险相依的信度模型。
综合以上研究成果,本文研究平衡损失函数下具有两水平共同效应的信度保费估计,即个体风险和组合风险分别存在相依性。事实上,一个组合的索赔可以直接影响其他组合。例如,在汽车保险中,不同类型的汽车分布在不同的组合。在一恶劣的天气条件下,一个组合中的汽车和其他组合中的车辆发生碰撞而导致索赔,这是常见的。因此,有必要同时考虑组合风险的相依性。Ebrahimzadeh等[11]通过引入两水平共同效应的信度模型推广了Wen等[4]的结果,然而,他们只是用平方损失函数对保费和风险的合适程度进行刻画。因此,本文将在平衡损失函数下讨论具有两水平共同效应的信度估计。
1 模型假设与准备知识
考虑M个投资组合的保单合同,每个组合有K个投保人,且每个投保人有n年的索赔经历。定义Xmij为第m个组合中第i个投保个体在第j年的索赔金额,记随机矩阵Xm=(X′m1,X′m2,…,X′mi)′,表示投资组合的索赔矩阵m=1,2,…,M,其中Xmi被定义为第m个投资组合中第i个投保个体,记Xmi=(Xmi1,Xmi2,…,Xmin)′,表示个人i的索赔向量(i=1,2,…,K)。类似于经典的信度模型,本文的目标是在所有观测到的索赔经验X1,X2,…,XM下,预测下一时期的索赔Xmi,n+1。为了克服平方损失函数带来的误差过高或过低的不足,本文在平衡损失函数下,建立具有两水平共同效应的信度模型,给出Xmi,n+1的信度估计。下面给出模型所需要的假设。
假设1 共同效应随机变量Γ具有已知的数学期望和方差。
假设2 随机矩阵Xm,m=1,2,…,M相互独立且同分布。
假设3 对固定的组合m,给定Γ,共同效应随机变量Λm的期望和方差分别为:
EΛmΓ=μλ(Γ),
假设4 对组合m和个体i,风险参数Θmi是独立同分布的。
假设5 给定Γ,随机变量Θmi,Λm独立同分布。
假设6 对固定的组合m与固定的个体i,给定Γ和Λm,随机变量(Xmi,Θmi)独立同分布。
假设7 对固定的组合m和固定的个体i,给定Γ,Λm和Θmi,索赔Xmi1,Xmi2,…,Xmin独立同分布且:
EXmin|Θmi,Λm,Γ=μ(Θmi,Λm,Γ),
Var(Xmin|Θmi,Λm,Γ)=σ2(Θmi,Λm,Γ)。
此外,记
EμΘmi,Λm,Γ|Λm,Γ=μΛm,Γ,
EμΛm,Γ|Γ=μ(Γ),
EμΓ=μ,
为统计目标保费δ0miX,记
Eδ0miX=μ,
Covδ0miX,Xljt=dmilj,
此外,记
与经典的信度模型类似,基于所有历史索赔X1,X2,…,XM估计未来保费Xmi,n+1的非齐次信度,必须解决下列最优问题:
(1)
令L(X,1)和Le(X)分别表示样本的非齐次与齐次函数类:
LX,1=
(2)

(3)
且
(4)
引理1 在假设1—假设7下,有以下结论:
(1)Xmi的期望为
E(Xmi)=μ1n,
m=1,2,…,M;i=1,2,…,K。
(5)
式中1n表示n个元素都为1的列向量。
(2)X的协方差矩阵为
(6)
式中⊗表示矩阵的kronecker积。
(3)历史索赔X和未来索赔Xmi,n+1的协方差矩阵为
(7)
式中em和ei分别是第m个和第i个元素为1,其他元素都为0的向量。
(4)X的协方差矩阵的逆矩阵为
(8)
其中
以上证明可参考文献[11]。
为得到未来索赔Xmi,n+1的非齐次与齐次信度估计,引理2、引理3给出关于随机变量在线性空间的投影及平滑公式,其证明可参考文献[2]。
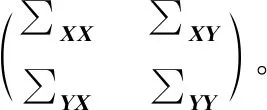
则有使EY-A-BY-A-BX′在矩阵的非负定意义下达到的最小解为:
由引理2可知,Xmi,n+1在L(X,1)和Le(X)上的最优估计分别为:
(9)
(10)
式(9)与式(10)分别表示Xmi,n+1在X上的非齐次投影与齐次投影。
对于退化的随机变量Xmi,n+1=E(Ymi) ,∑YmiX=0,式(10)可以简化为
(11)
引理3对于任意的两个闭集M⊂M′∈L2,随机变量Y∈L2,则有
projY|M′=projprojY|M|M′。
2 信度估计
为得到Xmi,n+1的非齐次信度估计,需求解式(1),利用正交投影的方法,得到未来保费Xmi,n+1信度估计。
定理1在假设1—假设7及引理1、引理2下,Xmi,n+1的最优非齐次信度估计为
Zi2-Zi3-Zi4-Zi5)μ,
(12)
其中
证明引入变量
Ymi=ξδomiX+1-ξXmi,n+1,
其中ξ是一个与其他随机变量相互独立的随机变量,且Pξ=1=1-Pξ=0=ω,ω是权重,所以式(1)等价于
(13)
根据引理2,可知Xmi,n+1的信度估计为
(14)
由Ymi定义可知
EYmi=EξδomiX+1-ξXmi,n+1=
EEξδomiX+1-ξXmi,n+1|ξ=
ωEδomiX+1-ωEXmi,n+1=μ。
(15)
注意到,EX|ξ=EX,从而Cov(EYmi|ξ,EX|ξ)=0。
所以
∑YmiX=ωCovδomiX,X+
1-ωCovXmi,n+1,X=
1-ω∑Xmi,n+1X。
(16)
结合引理1,可得
μ+ωG1+1-ωG2。
(17)
注意到
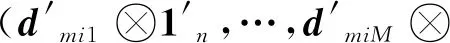
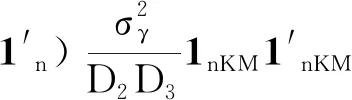
(18)
借用Ebrahimzadeh[11]中的结论
所以
(19)
结合式(17)—式(19)可得


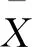
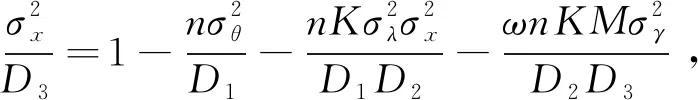
当μ未知时,定理1不能直接运用,需将式(1)的估计限制在样本的齐次函数类中计算它的齐次信度估计。


证明由引理3,可知
projprojXmi,n+1LX,1LeX,
(21)

Zi3-Zi4-Zi5)proj(μLeX,
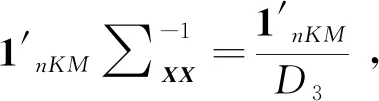
从而式(20)成立。
注1 在定理1中,当ω=0时,则可得到平方损失函数下具有两水平共同效应的信度估计:
1-Z1-Z2-Z3μ,
(22)
其中信度因子为:
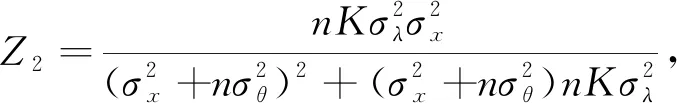
Z3=
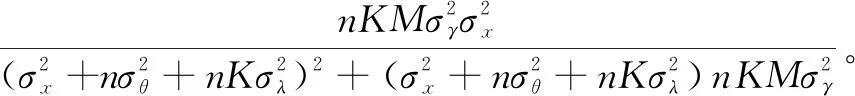
这便是Ebrahimzadeh[11]中的结果,可以说定理1是其的推广。
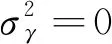
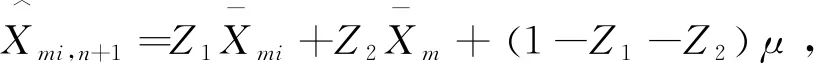
(23)
其中信度因子为:
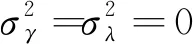

(24)
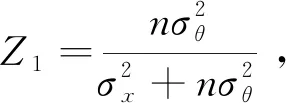
3 参数估计
命题1结构参数μ的无偏估计为
(25)
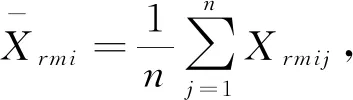
由于
EμΘmi,Λm,Γ=μ,
则
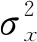
(26)
证明记Θm=(Θmi,…,ΘmK)′和
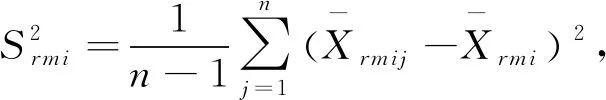
σ2Θmi,Λm,Γ,
从而
所以,结构参数σx的无偏估计为
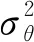
(27)
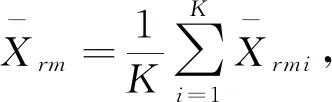
因为
注意到
所以
从而命题3得证。
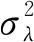
(28)
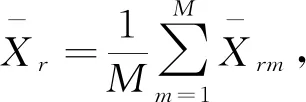
注意到
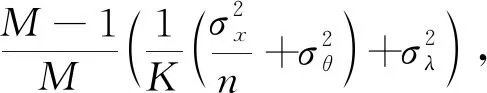
所以
(29)
证明记
利用条件方差公式,
从而
所以
4 结束语

