基于属性分割的高维二值数据差分隐私发布
2022-01-19洪金鑫吴英杰蔡剑平
洪金鑫 吴英杰 蔡剑平 孙 岚
1(福州大学数学与计算机科学学院 福州 350108)2(厦门华厦学院信息与智能机电工程学院 福建厦门 361024)
随着大数据产业的日趋成熟,在日常生活中有越来越多的数据被采集.通常这些数据蕴含着大量的隐私信息,例如交通数据中的个人移动轨迹、医疗数据中的病人患病记录等.如果直接使用这些数据很有可能会导致隐私的泄露.因此在使用时需要采取一些措施来保证数据的隐私安全.
差分隐私[1-5]是一种严格可证的隐私保护技术,它通过向数据注入满足特定分布的噪声干扰,使攻击者难以对特定的隐私数据进行精确的计算.经过扰动后的数据仍然保留着原始的统计学特征,但攻击者无法重构出真实的原始数据.这样便能够在保证数据安全的前提下,提高数据共享和使用的效率.
高维数据的隐私发布问题一直以来都是差分隐私领域里的一个研究热点与难点问题.如何在有效地保护数据中隐私信息的同时保证数据的可用性是该问题的研究重点.当前已有许多基于差分隐私的高维数据发布方法,这些方法大体上可以分成2类:
1)通过对高维数据进行降维来减小扰动原始数据时产生的噪声大小,主要包括主成分分析[6-9]、随机投影[10-13]、仿射变换[14]、截断分组[15-16]、PriView视图[17]等方法.
2)通过构建数据集的概率图模型来计算数据属性间的概率分布,然后对概率分布进行加噪,并用来生成合成数据发布,以此来避免直接扰动原始数据时产生的巨大噪声干扰.这类方法主要有朴素贝叶斯分类器[18]、贝叶斯网络[19-25]、Markov网络[26-28]等.
第1类方法(降维方法)是一个比较简单有效的方法,但是该类方法无法发布一个完整的高维数据集,这也限制了它的作用范围.一般这类方法主要用于回答一些查询操作或者作为数据挖掘、机器学习等领域的预处理方式.
第2类方法(概率图模型方法)通过生成合成数据的方式,能够发布一个完整的高维数据集,这使得它的适用范围更加广泛.
虽然现有的概率图模型方法在一定程度上能够解决高维数据的隐私发布问题,但当它应用于实际场景时,这些方法仍然存在着一些问题:
第一,这些方法都过于统一地认为属性间是相互独立或是相互关联的.其实对于不同的数据集来说,它们属性间的关联性是不一样的,有的属性间是具有联系的,有的属性间是相互独立的.为了能够让构建的概率图模型更符合真实的分布规律,就不能对这些关联性不同的属性一概而论.而是需要找到一种能够识别属性间不同关联性的方法,并以此来将不相干的属性分开处理.
第二,实现这些方法所需的时间复杂度普遍偏高.尤其是在构建概率图模型的过程中,大部分方法都使用了指数级时间复杂度的算法.虽然理论上这些方法都可适用于任意维度的高维数据,但是在实际使用时由于时间因素的影响,大多数的方法都只能处理到中低维数据,这明显无法满足实际应用的需求.
第三,这些方法中很少有针对高维二值数据的方法,以致于忽视了高维二值数据中存在的可以利用的性质,例如利用条件概率在二值数据上的取值特点.导致在对概率分布加噪时很容易出现概率值大规模失真问题,使得后续由该概率分布生成的合成数据的精度下降.
为解决上述3个问题,本文提出了PrivSCBN(differentially private spectral clustering Bayesian network)方法.本文的主要贡献包括4个方面:
1) 为了解决高维二值数据的差分隐私发布问题,本文提出了一种满足差分隐私的高维二值数据发布方法PrivSCBN.该方法由3个子算法组成,每个子算法都满足差分隐私的定义.然后基于每个子算法的噪声公式,设计了一种策略来分配隐私预算ε.最后,通过实验验证了PrivSCBN方法在时间性能和发布精度上都要优于现有的发布方法.
2) 为了解决不同属性间关联性不一致的问题.本文针对高维二值数据,设计了一种基于Jaccard距离的属性间关联程度衡量指标,并从理论论证了相比于常用的互信息,Jaccard距离在二值数据属性上拥有更低的全局敏感度和更高的准确度.然后基于该衡量指标,本文提出了一种满足差分隐私的谱聚类(differentially private spectral clustering, DPSC)算法来对数据属性进行合理的划分,然后根据划分结果进一步分割原始数据集,以此达到独立属性分开处理和数据降维的双重目的.
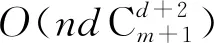
4) 为了解决概率分布加噪时容易出现的概率值失真问题.本文利用贝叶斯网络最大入度数的限制和条件概率在二值数据上的取值特点,提出了一种概率分布加噪算法BNC(binary noisy conditionals)来为每个从贝叶斯网络中提取的概率分布进行加噪,在一定程度上减少了出现概率值失真的问题.
1 相关工作
目前,概率图模型方法已取得了一些研究成果.
Qardaji等人[17]针对高维二值数据的隐私保护问题提出了PriView方法,该方法假设所有属性都是相互独立,通过构建一组带噪声的View视图来回答用户的α-way查询.Zhang等人[19-20]针对高维数据隐私发布问题提出了PrivBayes方法,该方法认为属性间都是相互关联的,通过贪心算法GreedyBayes来构建贝叶斯网络,然后利用贝叶斯网络和拉普拉斯机制计算出属性间带噪声的条件分布,并通过贝叶斯网络的近似推理来计算出所有属性的联合分布,最后基于这个联合分布来生成合成数据发布.在PrivBayes方法的基础上,加权PrivBayes[21]、平滑PrivBayes[22]、PrivBayes_Hierarchical[23]等一系列方法被相继被提出.王良等人[21]提出了加权Priv-Bayes方法,该方法认为不同属性的敏感程度是不一样的,并不能一概而论,因此该方法通过为每个属性分配一个权值,然后在构建贝叶斯网络的过程中优先选择权值高的属性结点,以此来构建更好的贝叶斯网络.Li等人[22]提出了平滑PrivBayes方法,该法方法引入了差分隐私的平滑敏感度机制,使其能够在牺牲部分隐私保护程度的情况下减少产生的噪声大小,从而提高联合分布的精度.郝志峰等人[23]提出了PrivBayes_Hierarchical方法,该方法利用语义树来对数据属性的语义层次关系进行抽象,然后在构建贝叶斯网络的过程中考虑父结点的语义层级对子结点的影响,从而能够平衡数据的可用性与安全性.
除了基于贝叶斯网络的有向图模型方法,还有基于Markov网络的无向图模型方法.Chen等人[26]提出了Jtree方法,该方法先是使用基于稀疏向量的采样技术来探索属性间的关系,然后基于这些关系来构建Markov网络,接着将该网络分割成若干个完全团,并基于这些完全团通过联合树算法和拉普拉斯机制计算出属性间带噪声的联合分布.张啸剑等人[27]在Jtree方法的基础之上提出了PrivHD方法,该方法通过高通滤波技术来加速Markov网络的构建,然后利用最大生成树算法来构建更好的联合树.
从这些分析中可以看出,现有的概率图模型方法主要集中在研究如何更好更快地构建概率图模型、减少产生的噪声干扰、获得更准确的概率分布值,从而生成更高精度的合成数据.但是这些方法仍然存在着时间复杂度过高、没有考虑属性间不同程度的关联性、注入的噪声过大导致概率值失真等问题.为此本文提出了PrivSCBN方法来进行解决.
2 理论与定义
2.1 差分隐私
定义1.ε-差分隐私[1].设兄弟数据集D和D′,它们彼此相差1条记录.给定1个随机算法A,若A满足ε-差分隐私,则有
Pr[A(D)=O]≤exp(ε)×Pr[A(D′)=O],
(1)
其中,ε表示隐私预算,预算越小则隐私的保护程度就越高.Pr[A(D)=O],Pr[A(D′)=O]分别表示算法A在数据集D和D′上输出为O的概率.
实现差分隐私的机制主要有拉普拉斯机制[2]和指数机制[3].这2种机制产生的噪声大小与查询函数的全局敏感度有关.
定义2.全局敏感度[2].设查询函数f:D→n,其全局敏感度定义为

(2)

定理1.拉普拉斯机制[2].设查询函数f:D→n,给定1个随机算法A,若A满足ε-差分隐私,则有
A(D)=f(D)+Lap(Δf/ε),
(3)
其中,Lap(Δf/ε)表示满足拉普拉斯分布的噪声变量.隐私预算ε越大或全局敏感度Δf越小,产生的噪声就越小.
定理2.指数机制[3].设评分函数u(x)表示输出结果为x的评分,给定一个随机算法A,若A满足ε-差分隐私,则有
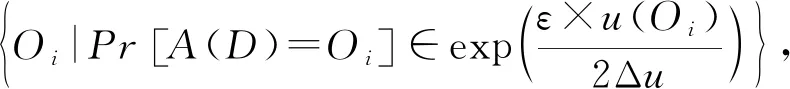
(4)
其中,Δu表示评分函数u(x)的全局敏感度.输出Oi的评分越高,则被选中的概率就越大.
此外,在设计和证明满足差分隐私的算法过程中,需要用到2条重要的差分隐私组合性质.

性质2.并行组合性质[4].给定数据集D,将D分割成m个互不相交的子集D={D1,D2,…,Dm}.设算法A1(D1),A2(D2),…,Am(Dm)均各自满足ε-差分隐私,并且任意2个算法的随机过程相互独立.那么这些算法的组合算法A也满足ε-差分隐私.
2.2 谱聚类
谱聚类(spectral clustering)[28]是一种基于图论的分割式聚类方法,通常能够收敛于全局最优解.它的作用机理是先将数据集映射成一张带权无向图,然后通过对图中的结点进行分割,使得子图内部的结点尽量相似,子图外部的结点尽量不同.
标准的谱聚类算法实现过程如算法1所示:
算法1.谱聚类算法.
输入:数据集D={x1,x2,…,xn}、类簇个数k、尺度参数σ;
输出:分割结果集C={C1,C2,…,Ck}.
① 使用式(5)计算n×n的距离矩阵W:
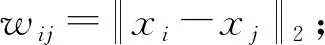
(5)
② 使用式(6)计算n×n的相似度矩阵A:
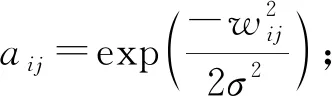
(6)
③ 使用式(7)计算n×n的度矩阵B:
(7)
④ 计算拉普拉斯矩阵L=B-1/2(B-A)B-1/2;
⑤ 计算L的特征值,然后从小到大排序,取前k个特征值计算其特征向量u1,u2,…,uk;
⑥ 将k个特征向量(列向量)组成n×k的矩阵U=(u1,u2,…,uk),令yi为矩阵U的第i行向量,并对其进行单位化yi=yi/|yi|;
⑦ 使用k-means聚类算法对新样本点Y={y1,y2,…,ym}进行划分得到划分结果C;
⑧ returnC.
算法1中的拉普拉斯矩阵L是对称的半正定矩阵,可以计算出n个非负实数的特征值和n个对应的特征向量.因此,该算法最终一定可以得到k个聚类的结果.
2.3 贝叶斯网络
贝叶斯网络(Bayesian network)是一种概率图模型,主要用来探索一组随机变量之间的关系.贝叶斯网络通常使用1张有向无环图来表示,图中结点代表随机变量、边代表随机变量之间的关系.
例如图1是1张拥有5个结点的贝叶斯网络图,该网络的最大入度数为3.
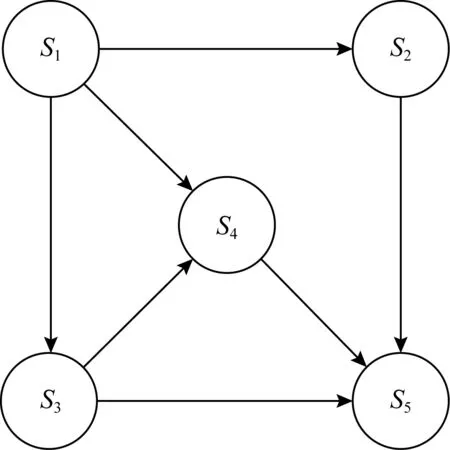
Fig. 1 Bayesian network of 5 nodes
一般给定一组属性S={S1,S2,…,Sm},由条件概率的链式法则可得这组属性的联合分布为
Pr[S]=Pr[S1]×Pr[S2|S1]×…×Pr[Sm|S1,…,Sm-1],
(8)
通过贝叶斯网络可将该联合分布近似为
(9)

表1显示了图1中各个结点的父结点集:

Table 1 Parent Set of Each Node in Bayesian Network
利用式(9),可得该属性集的近似联合分布为
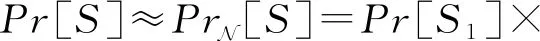
(10)
实际上越复杂的贝叶斯网络所蕴含的信息就越丰富,计算出来的联合分布也会越接近真实的分布规律.但由于时间因素的影响,通常在构建贝叶斯网络时会限制整个网络的最大入度数,以此来降低构建网络所需的时间成本.
2.4 互信息
互信息常用来表示1个变量由于已知另一个变量所能减少的不确定程度.互信息也可以用于衡量2个属性间的相互依赖程度.互信息越大,则属性间的相互依赖程度就越高.
定义3.互信息.给定2个离散的随机变量X∈{x1,x2,…,xn},Y∈{y1,y2,…,ym},它们间的互信息为
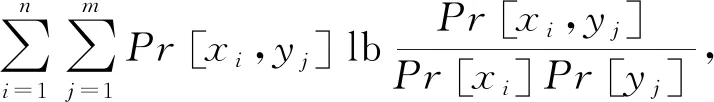
(11)
其中,Pr[xi,yj]表示随机变量X,Y取值为xi,yj的联合分布.当I(X,Y)→0时,有Pr[xi,yj]→Pr[xi]Pr[yj],即随机变量X与Y接近于相互独立.
2.5 Jaccard距离
Jaccard距离常用来表示2个集合间的差异程度.距离越小,集合间的差异程度就越小.
定义4.Jaccard距离.给定2个集合X,Y,它们之间的Jaccard距离为
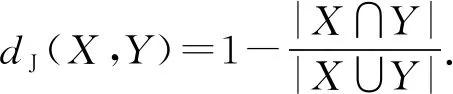
(12)
Jaccard距离也可以用来表示同一数据集中2个二值属性间的差异程度.
假设给定2个二值属性X,Y,它们取值为X=1,Y=1的数据量为n11,取值为X=0,Y=1的数据量为n01,取值为X=1,Y=0的数据量为n10.那么这2个属性之间的Jaccard距离为
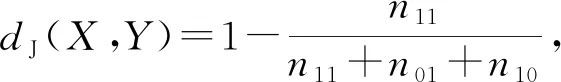
(13)
可以看出距离越小,属性间的关联程度就越高.
3 PrivSCBN算法
3.1 概 述
PrivSCBN算法的整体流程如图2所示:
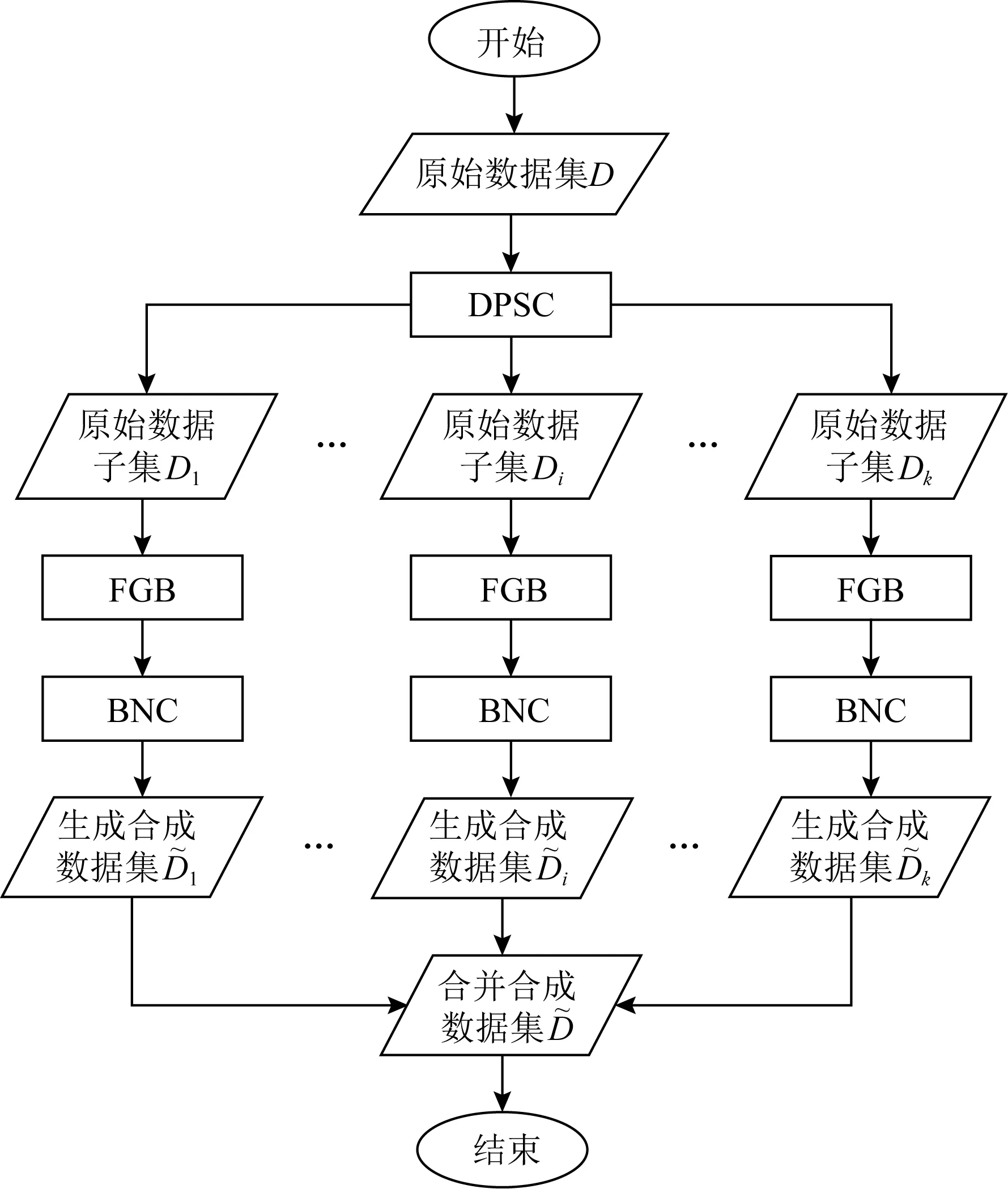
Fig. 2 PrivSCBN algorithm flowchart
PrivSCBN算法的实现过程如算法2所示:
算法2.PrivSCBN算法.
输入:数据集D={x1,x2,…,xn}、属性集S={S1,S2,…,Sm}、类簇个数k、尺度参数σ、最大入度数d、隐私预算ε;
① 计算a1=(m-1)/(n-1),a2=2m/(nk),a3=2m/(nk),并计算a=a1+a2+a3;
② 计算ε1=(a1/a)ε,ε2=(a2/a)ε,ε3=(a3/a)ε;
③ 求属性划分结果集C={C1,C2,…,Ck}←DPSC(D,S,k,σ,ε1);
④ 依据C分割原始数据集D={D1,D2,…,Dk};
⑥ fori=1 tokdo
⑩ end for
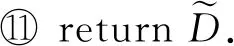
PrivSCBN算法可以拆解成4个独立的步骤:
1) 通过DPSC算法将属性集S划分成k个属性子集C1,C2,…,Ck,然后根据这些子集将原始数据集D分割成k个互不相交的数据集子集D1,D2,…,Dk.
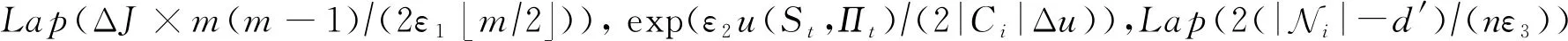
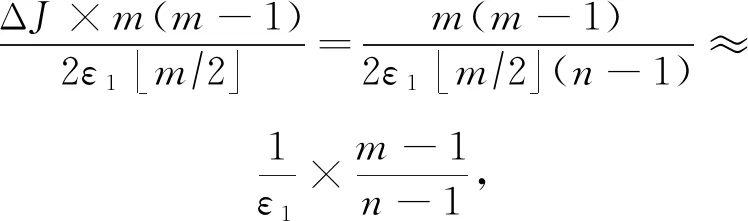
(14)

(15)
(16)
故可得隐私预算ε1,ε2,ε3的分配策略为ε1=(((m-1)/(n-1))/a)ε,ε2=((2m/(nk))/a)ε,ε3=((2m/(nk))/a)ε,而a=(m-1)/(n-1)+2m/(nk)+2m/(nk).
最后,说明PrivSCBN算法满足ε-差分隐私.由3.2~3.4节的最后一段满足差分隐私性质的说明可知,步骤③⑦⑧中的DPSC,FGB,BNC算法均各自满足ε1,ε2,ε3-差分隐私.虽然其中的FGB和BNC算法会被执行k次,但每次执行所使用的数据集Di之间是没有交集的.由性质2可知,它们仍然满足ε2,ε3-差分隐私.并且除了上述的3个算法之外,PrivSCBN算法没有其他地方再涉及原始数据集D的使用.因此,由性质1可知,整个PrivSCBN算法满足ε=(ε1+ε2+ε3)-差分隐私.
3.2 差分隐私谱聚类算法
由于高维数据的来源非常广泛,其属性间的关系错综复杂,即有的属性间是具有联系的、有的属性间是相互独立的.一般在构建概率图模型时,是希望模型能够很好地反映出这些属性间的关系.但由于高维数据中可能存在着毫无因果关系的属性对,而如果将这些属性对放到一起来构建概率图模型,那么得到的模型将无法很好地反映真实的分布规律.因为,这时引入了一些全局无关的变量(属性),导致模型为这些无关的变量建立了有关的联系.举个例子,给定一个属性集S,满足下标奇偶性相同的属性间是具有联系的、奇偶性不同的属性间是相互独立的.如图3所示:
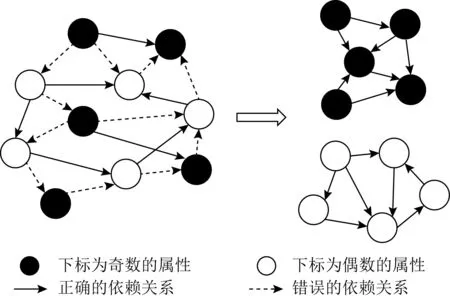
Fig. 3 Black and white node network diagram
从图3可以看出通过将黑白结点分开并分别构建网络图,可以消除图中所有错误的依赖关系.当然这是在能够将黑白结点完全区分开来的最理想条件下实现的,但在一般情况下是无法完全将它们区分开的.因此,如何找到一种较好的区分方法是本文研究的重点.为此本文提出了一种满足差分隐私的谱聚类算法DPSC来对数据集属性进行合理的划分.
考虑如何衡量属性间的关联程度,一个比较常用的方法是使用互信息来进行衡量.但是这在处理高维二值数据时可能遇到一个问题,那就是高维二值数据通常是稀疏型数据,其中存在大量同时取值为0的属性对.而在一般的高维二值数据中能够反映出客观规律的是同时取值为1的属性对.因此,如果使用互信息来作为衡量指标,那么会很容易得出所有属性都是具有联系的这种无效结论.而由式(13)可知Jaccard距离是不会考虑这种情况的,并且它也能很好地反映出2个属性间的差异程度.因此,DPSC算法采用Jaccard距离来作为属性间关联程度的衡量指标.
DPSC算法的实现过程如算法3所示:
算法3.DPSC算法.
输入:数据集D={x1,x2,…,xn}、属性集S={S1,S2,…,Sm}、类簇个数k、尺度参数σ、隐私预算ε1;
输出:属性划分结果C={C1,C2,…,Ck}.
① 使用式(17)计算m×m的距离矩阵W:
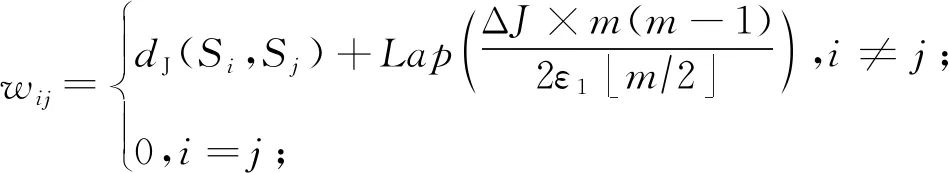
(17)
② 执行算法1的步骤②~⑥;
③ 使用k-means++聚类算法对新样本点Y={y1,y2,…,ym}进行划分得到划分结果C;
④ returnC.
DPSC算法先将属性集S映射成一张带权无向图.图中以每个属性Si(1≤i≤m)作为顶点,以属性间的关联程度作为边权,边权使用的是属性间的Jaccard距离进行度量.由于在计算边权时涉及到了原始数据集D的使用,为了保护数据中的隐私信息不被泄露,我们需要对计算结果进行扰动.这里使用拉普拉斯机制来进行扰动,扰动所产生的噪声大小与边权函数的全局敏感度有关.因此,我们需要先考虑Jaccard距离的全局敏感度大小.
定理3.Jaccard距离的全局敏感度为ΔJ=1/(n-1).
证明.根据式(13),不失一般性地假设n11+n01+n10=n,并且令x=n11.考虑减少一条记录给dJ(X,Y)带来的影响,存在2种情况:
1) 减少的是X=1,Y=1的记录,根据式(2)有
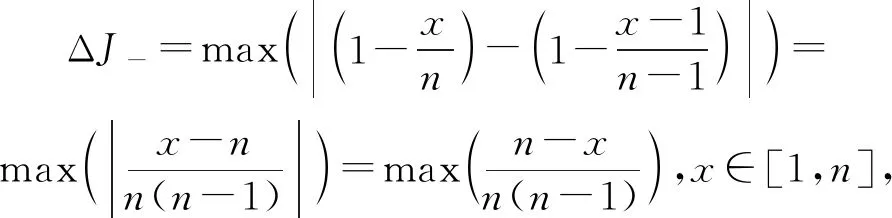
(18)
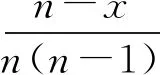
2) 减少的是X=0,Y=1或X=1,Y=0的记录,同样由式(2)有
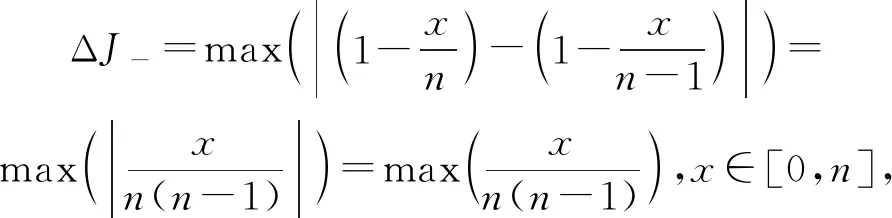
(19)
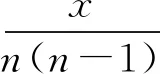
同理,当增加一条记录时,有ΔJ+=1/(n-1)成立.
综上所述,Jaccard距离的全局敏感度为ΔJ=max(ΔJ-,ΔJ+)=1/(n-1).
证毕.
实际上对于互信息,由Zhang等人[19]的论文可知,互信息在二值属性上的全局敏感度ΔI为
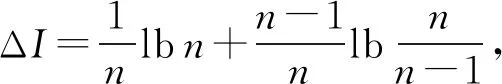
(20)
很明显相对于Jaccard距离ΔJ=1/(n-1)的全局敏感度,互信息的全局敏感度要来得更大.根据式(3)可知相比于互信息,使用Jaccard距离产生的拉普拉斯噪声大小会更小.
在确定完边权的全局敏感度之后,DPSC算法会对每个边权值进行加噪,这个加噪过程会进行多次.由性质1可知每次加噪都需要分配一部分的隐私预算.因此需要先确定加噪的总次数,即构建距离矩阵W总共需要查询原始数据集D的次数.


综上所述,我们可以得到加入边权函数的拉普拉斯噪声大小为
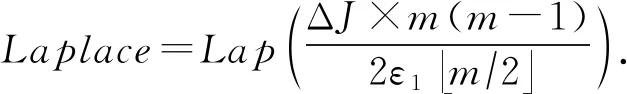
(21)
此外DPSC算法为了能够进一步提升属性的聚类效果,我们将原本算法1步骤⑦使用的k-means聚类算法换成了k-means++算法.该算法在初始点的选择上更为合理,因此能够产生更好的聚类效果.
在聚类完成后,算法会根据得到的样本点Y的聚类情况,按照样本点y1对应属性S1,样本点y2对应属性S2,…,样本点ym对应属性Sm的对应规则,将每个属性分配到其所对应的样本点所在的类簇中,这样就完成了对数据属性的划分.

3.3 差分隐私贝叶斯网络算法
在现有的贝叶斯网络模型方法中,大多都是使用由Zhang等人[19]提出的GreedyBayes算法来构建贝叶斯网络.该算法基于贪心的思想,即通过枚举所有的情况,选择能够使整个贝叶斯网络的互信息量达到最大的网络结构进行构造.
GreedyBayes算法的实现过程如算法4所示:
算法4.GreedyBayes算法.
输入:数据集D={x1,x2,…,xn}、属性集S={S1,S2,…,Sm}、最大入度数d;
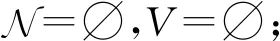
③ fori=2 tomdo
④ 初始化集合Ω=∅;
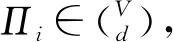
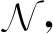
⑦ end for
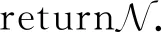
由于Zhang等人[19]在论文中没有给出该算法具体的时间复杂度公式,故本文先对GreedyBayes算法的时间复杂度进行论证.
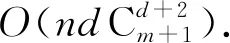

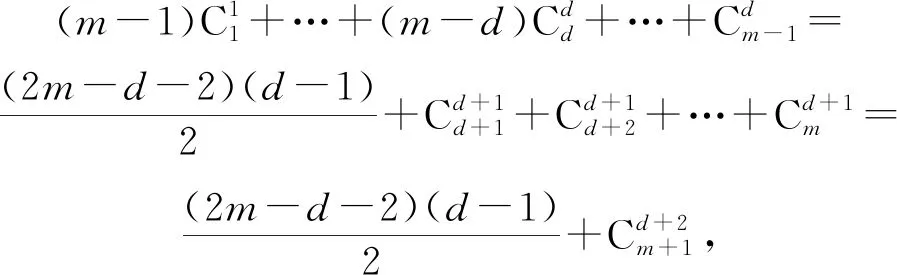
(22)
在最坏情况下,即d+2=(m+1)/2时,有
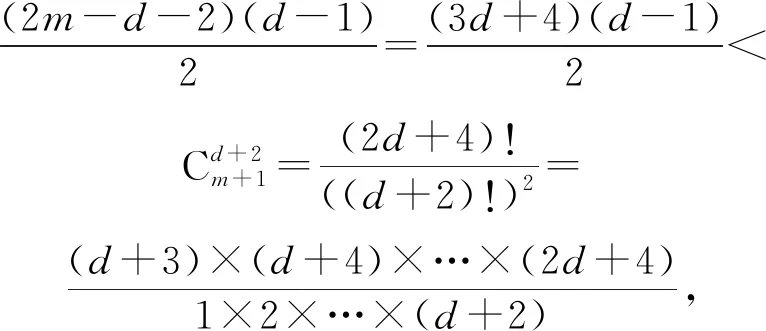
(23)
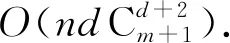
证毕.
很明显由于时间复杂度的影响,GreedyBayes算法仅能适用于属性维度m较小或者贝叶斯网络最大入度数d很小的情况.
为了能够更直观地说明,我们以含有50个属性的数据集为例.当贝叶斯网络的最大入度数d分别为5,10,15,20,25时,GreedyBayes算法所需要枚举的(Si,Πi)对的个数如表2所示:

Table 2 Enumeration Number of GreedyBayes Algorithm
从表2中可以看出,假设计算机每秒可以计算1万个(Si,Πi)对的互信息.当最大入度数d=10时,就已经需要184天每天24 h的不间断处理才能完成.而当d=25时,就变得连计算机也无法解决,因为它一共需要728年零11天每天24 h的不间断处理时间才能完成任务.
为了能够“真正”地处理高维数据、构建更复杂的贝叶斯网络,本文提出了一种简洁高效的贝叶斯网络快速构建算法FGB.该算法只需要O(nm2d2)的时间就能够构建出一个完整的贝叶斯网络.
FGB算法的实现过程如算法5所示:
算法5.FGB算法.
输入:数据集子集Di={x1,x2,…,xn}、属性子集Ci={S1,S2,…,S|Ci|}、最大入度数d、隐私预算ε2;
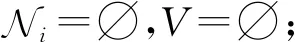
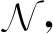
③ fort=2 to |Ci| do
④ 初始化集合Ω=∅;
⑤ 对每个Sj∈CiV和Πj←DPBestParent(Di,Sj,fa,min(t-1,d)),将(Sj,Πj)加入Ω;
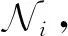
⑦ end for
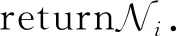
由算法4和算法5可知,FGB与GreedyBayes算法的一个主要区别在于步骤⑤求解每个待选结点的最佳父结点集的过程.FGB使用了一个时间复杂度为O(nd2)的算法DPBestParent来进行求解.而GreedyBayes算法是通过枚举所有的情况,然后从中选择最优的.实际上在枚举的过程中是存在着大量的重复计算和无意义计算的.而FGB算法利用了动态规划的记忆化手段和最优子结构特性,在保证解是当前最优解的前提下极大地减少了大量的重复计算和无意义计算.这在很大程度上提升了贝叶斯网络的构建速度.
DPBestParent算法的实现过程如算法6所示:
算法6.DPBestParent算法.
输入:数据集Di={x1,x2,…,xn}、属性Sj、新增父属性fa、当前最大入度数d′;
输出:最佳父属性集Πj.
①dp[Sj,0]=∅;
② forl=d′ to 1 do
③Π′=dp[Sj,l-1]∪fa;
④Π″=dp[Sj,l];
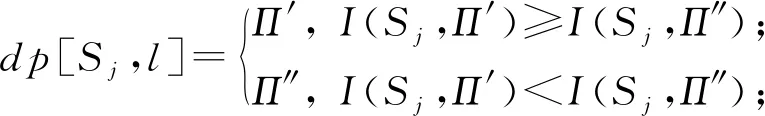
⑥ end for
⑦Πj=dp[Sj,d′];
⑧ returnΠj.
算法6中dp[Sj,l]表示结点集合,含义是结点Sj选择l个结点作为父结点的最佳选择情况.从步骤②~⑥的for循环中可以看出,实际上在新一轮的DPBestParent算法执行时,dp[Sj,l]就已经记录了上一轮中在该状态下的最佳父结点集的选择情况.因此对于本轮来说,只需要关心上一轮新加入网络的结点fa对当前最佳父结点集的选择情况的影响即可.这里for循环采用的是倒序遍历的方式,即从d′到1.其原因是为了保证当前更新的状态不会影响到下一次的状态更新,这个操作避免了结点fa被加入到同一个父结点集多次.
接下来证明FGB算法的时间复杂度.
定理5.FGB算法的时间复杂度为O(nm2d2).
证明.FGB算法的时间消耗主要集中在步骤③~⑦的for循环.该for循环一共会执行|Ci|-1次.
对于步骤⑤,循环每次执行时都会调用|Ci|-t(t∈[1,|Ci|-1])次 DPBestParentSet子算法,而每次调用子算法所需的时间为O(nd2).因此,执行完|Ci|-1次步骤⑤所需的总时间复杂度为O(n|Ci|2d2).
对于步骤⑥,循环每次都会为|Ci|-t个待选组合(St,Πt) 计算其被选择的概率Pc(St,Πt),而每次计算所需的时间为O(nd).因此,执行完|Ci|-1次步骤⑥所需的总时间复杂度为O(n|Ci|2d).
又因为每个属性子集的大小|Ci|∝m.因此,整个FGB算法的时间复杂度为O(nm2d2).
证毕.
除了解决GreedyBayes算法在执行效率上的问题之外,FGB算法还引入了差分隐私指数机制来扰动贝叶斯网络的构建过程(步骤⑥),从而解决了构建的贝叶斯网络存在隐私泄露风险的问题.
差分隐私指数机制的思想是依据评分函数以一定的概率来选择当前加入贝叶斯网络的(Si,Πi)对.我们使用互信息I来作为指数机制的评分函数u(S,Π)=I(S,Π).当(S,Π)对的互信息越大时,评分函数u(S,Π)的值就越高,则被选择的概率也就越大.由式(20)可知,该评分函数的全局敏感度为
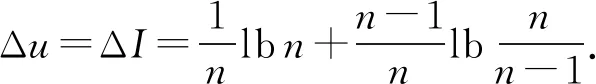
(24)
虽然Zhang等人[19]在PrivBayes方法中提出了一种全局敏感度更低的评分函数F,其全局敏感度仅为ΔF=1/n.但计算该评分函数所需的时间为O(n2d),仅能适用于构建d较小的贝叶斯网络.因此本文不采用该方法,仍然使用互信息作为评分函数.
在执行FGB算法之前,PriveSCBN算法(算法2)的步骤④会将原始数据集D分割成k个相互独立的数据集子集Di.由性质2可知,处理这些子集的过程可以共享同一个隐私预算.
FGB算法会执行步骤⑥共|Ci|-1次,每次都需要使用指数机制从Ω中选择一个(St,Πt)对加入贝叶斯网络.由性质1可知,每次选择都会消耗一部分的隐私预算.这里采用平均分配的方式,即将隐私预算ε2平均分成|Ci|份.结合指数机制,可得概率值Pc(St,Πt)的表达式为

(25)
其中,u表示评分函数,Δu表示评分函数的全局敏感度,Ω表示当前所有可选的组合情况.
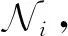
3.4 差分隐私条件分布计算
通过贝叶斯网络可以在很大程度上简化联合分布的计算过程,并且越好的贝叶斯网络计算出来的联合分布越接近真实值.但是如果直接使用贝叶斯网络来进行计算,很有可能会导致隐私的泄露.因此,我们需要对计算出来的联合分布做进一步的扰动,以此来达到保护隐私的目的.
Zhang等人[19]在论文中使用NoisyConditionals算法来实现贝叶斯网络的安全计算.该算法通过向每个结点与其父结点集的联合分布Pr[Sj,Πj]注入拉普拉斯噪声来得到带噪声的联合分布Pr*[Sj,Πj].虽然这样做能够保证联合分布是受差分隐私保护的,但当属性维度m较大或者属性的取值情况较多时,计算得到的联合分布的概率值会普遍偏小.而如果直接对这些较小的概率值注入噪声干扰的话,那么很有可能会导致这些概率值被完全覆盖,造成大规模的概率值失真问题,这将严重影响后续生成的合成数据的精度.因此,本文不直接采用NoisyConditionals方法,而是针对二值数据的取值特点提出了一种概率分布加噪算法BNC来实现贝叶斯网络的安全计算.
由于BNC算法每次处理的是一个数据集子集Di,由性质2可知,处理这些子集的过程可以共享同一个隐私预算. 因此,BNC算法的实现过程如算法7所示:
算法7.BNC算法.
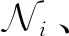
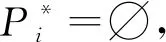
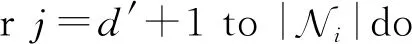
③ 求联合分布Pr[Sj,Πj]和边缘分布
Pr[Πj];
④ 求条件分布Pr[Sj|Πj]=Pr[Sj,Πj]/
Pr[Πj];
⑤ 对Pr[Sj|Πj]加入噪声得到
Pr*[Sj|Πj];
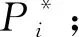
⑦ end for
⑧ forj=1 tod′ do
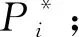
⑩ end for
从算法7中可以看出,BNC算法不会直接对联合分布进行加噪,而是改为对由联合分布和边缘分布计算得来的条件分布进行加噪.这里利用了条件概率在二值数据上的取值特点,即当分布为条件分布时,有以下式子成立:
PrSj=0|Πj=Oj+PrSj=1|Πj=Oj=1,
(26)
其中,Sj表示当前结点所对应的属性,Πj表示Sj的最佳父结点集所对应的属性集,Oj表示Πj的某个取值情况.
由式(26)可知,在条件概率Pr[Sj=0|Πj=Oj]和Pr[Sj=1|Πj=Oj]中至少会存在一个条件概率的概率值比较大或者2个条件概率的概率值相差不大即都在0.5上下.这样即使直接对条件概率注入噪声干扰,也至少存在一个较大的条件概率的概率值不会被完全覆盖.所以就不会出现2个概率值同时被覆盖的情况,除非是注入的噪声干扰原本就是非常大的,那在这种情况下即使采取任何措施也都无法避免概率值失真的情况发生.因此,利用条件概率在二值数据上的这个特点能够在很大程度上减少概率失真发生的次数.
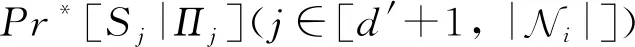
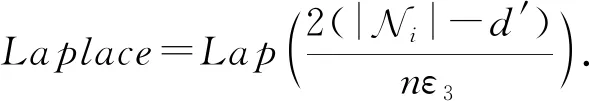
(27)
注意到BNC算法在步骤⑨中计算Pr*[Sj,Πj](j∈[1,d′])是直接基于Pr*[Sd′+1,Πd′+1]计算的,不会涉及原始数据集Di的使用.因此不需要对其加入拉普拉斯噪声干扰,这样可以节省下d′个隐私预算的分配.
除了利用条件概率在二值数据属性上的取值特点来减少概率失真发生的次数之外.根据式(27)可知,当贝叶斯网络的最大入度数d′在不断增加时,其所产生的拉普拉斯噪声大小也在逐渐减小.因此,BNC算法还允许使用者通过控制d′来减小产生的噪声大小,以此来进一步减少概率值失真发生的次数.
考虑到在对条件分布注入拉普拉斯噪声后,条件分布的概率值可能出现取值为负和每一对条件相同、取值相对的条件概率之和不为1的问题.BNC算法还会对加噪后的概率值进行“一致性处理”,即算法7中的步骤⑥,从而保障求出来的条件分布的概率值满足概率的基本性质.
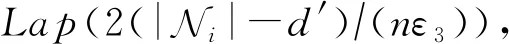
4 实 验
4.1 实验环境
本次实验使用C++编程语言来实现所有的方法,其中贝叶斯网络部分的实现参考了Zhang等人[20]论文的实验相关代码.
实验平台的具体配置信息如表3所示:

Table 3 Experimental Platform Configuration Information
4.2 实验数据集
实验采用3个真实的数据集NLTCS,ACS,Retail.其中NLTCS是一项美国长期护理调查记录,其中包括21 574名老年残疾人的日常生活、医疗情况;ACS是由IPUMS-USA所发布的全球人口普查和调查数据,记录了47 461条个人信息;Retail是美国零售市场的88 162条购物记录,每条记录包含其所购买的商品条目,总共有16 469种商品类别,我们从中选取了前50个销量最多的商品,并将它们处理成含有50个属性的高维二值数据集.这3个数据集的具体信息如表4所示:
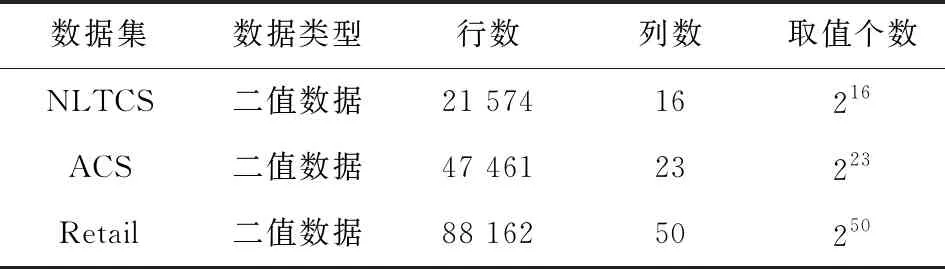
Table 4 Description of Datasets
4.3 评价指标
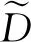
(28)
4.4 实验和结果
我们将通过3个不同的实验来验证PrivSCBN算法的高效性和可用性.
第1个实验是为了验证PrivSCBN算法中的FGB子算法与传统的GreedyBayes算法在构建贝叶斯网络的时间性能上的表现.实验将在NLTCS和ACS这2个数据集上进行100次随机的重复实验,贝叶斯网络的最大入度数d分别设置为2,3,4.对于FGB算法所需的隐私预算ε,由于不是本次实验关心的变量,因此我们将其恒定为1.实验结果将通过对比这2个算法构建贝叶斯网络的平均时间消耗来进行验证.实验结果如表5所示:

Table 5 Average Time Consumption Record
从表5中可以看出,FGB算法在时间性能上的表现要明显优于GreedyBayes算法,这是符合我们预期的.当d=2时,GreedyBayes算法的时间消耗是FGB的9倍(NLTCS)和18倍(ACS),并且随着d的增加这个倍数也在逐渐扩大.当d=3时是18倍和54倍,当d=4时是30倍和137倍.这个实验结果表明相较于传统的GreedyBayes算法,使用FGB算法来构建贝叶斯网络更为高效.
从另一个角度来看,不管是随着数据属性维度m的增加还是随着贝叶斯网络最大入度数d的增大,FGB算法的时间消耗增长幅度都要比Greedy-Bayes小很多.例如当d=2,m从16增加到23时,FGB的运行时间只扩大了5倍左右,而GreedyBayes的运行时间扩大了10倍左右.并且随着d的增加FGB的运行时间的增幅一直维持在5倍左右,而GreedyBayes的增幅是明显变大的,d=3时是15倍,d=4时是24倍.这个结果表明FGB算法在执行效率上具有一定的稳定性.
因此,以FGB算法作为核心子算法的PrivSCBN算法本身也具有高效性和一定的稳定性.
第2个实验是为了分析PrivSCBN算法的可用性.为了能够知道在无噪声环境下,PrivSCBN算法本身可能会产生的噪声大小.我们通过设置无差分隐私保护的NoPrivSCBN算法来与之进行对比.实验将在NLTCS,ACS这2个数据集上进行100次随机的重复实验,隐私预算ε分别设置为0.05,0.1,0.2,0.4,0.8,1.0.实验结果将通过200次随机的α-way查询进行验证,其中α的取值为3,8,12.实验结果如图4所示.
从图4中可以看出,即使是没有差分隐私保护的PrivSCBN算法也会产生一定的误差.其原因是PrivSCBN是一种贝叶斯网络模型方法,在构建贝叶斯网络的过程中,以及通过贝叶斯网络的近似推理求得的联合分布本身,还有使用联合分布生成的合成数据集,在这些过程中本身就会产生一定的误差.因此随着隐私预算ε的增加,PrivSCBN的误差逐渐逼近NoPrivSCBN的误差,这是符合差分隐私规律的.
注意到当隐私预算ε=0.05时,所有实验的查询误差都达到了很高的量级.而当ε增大时,这些查询误差开始呈明显的下降趋势.这是符合我们的预期的.因为当ε=0.05时,注入的噪声干扰是非常大的,这会使得大部分的概率值都出现失真问题,导致最后生成的合成数据的精度变得非常差.
通过进一步的观察我们发现随着隐私预算ε的增加,PrivSCBN算法的查询误差在快速地下降.最后会达到NoPrivSCBN的误差界限,并且大多都只需要较少的隐私预算就能达到.这个实验结果表明PrivSCBN具有较高的可用性.
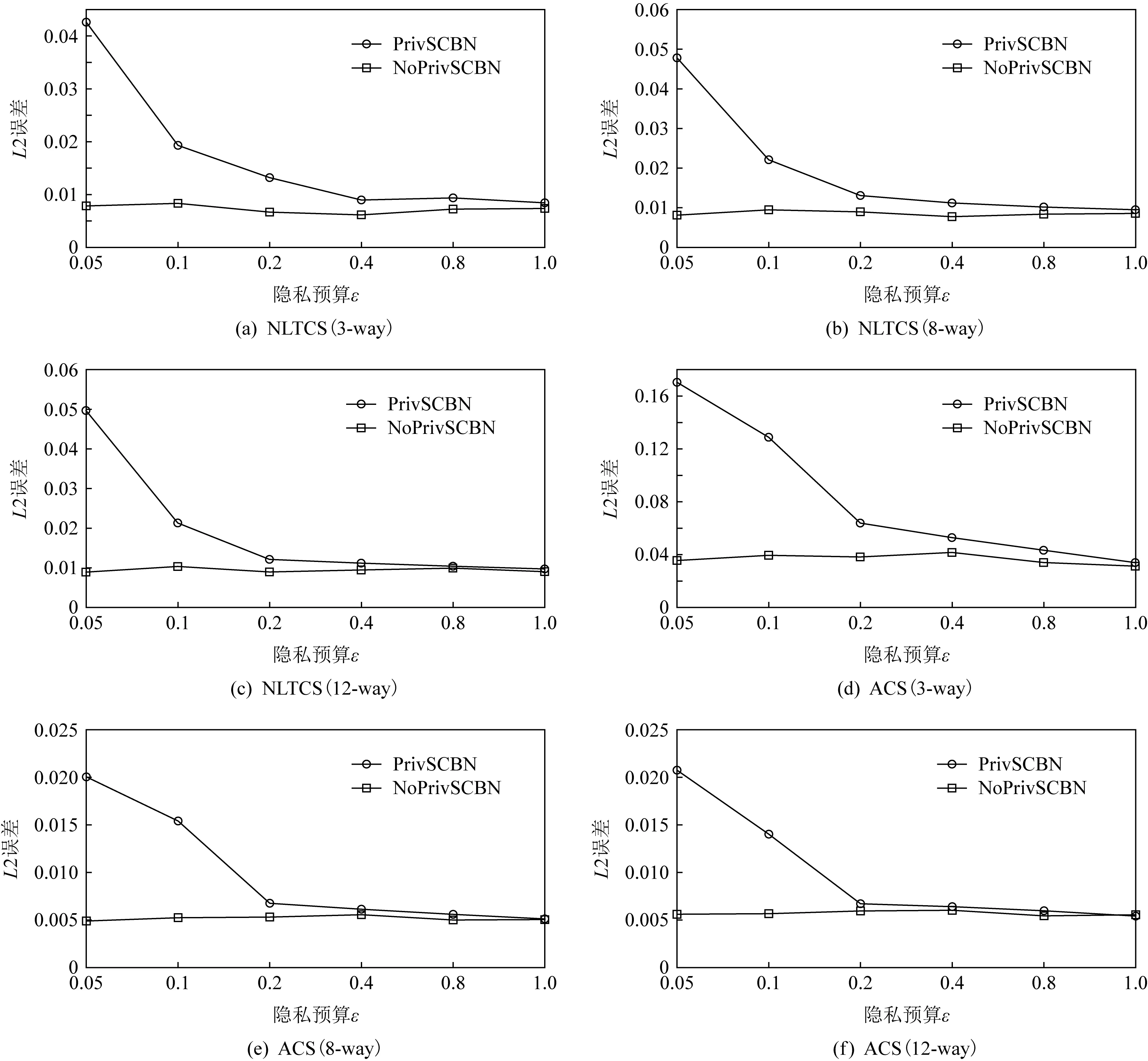
Fig. 4 Analysis of α-way query error with or without differentially private on NLTCS and ACS datasets
第3个实验是为了分析PrivSCBN算法在真正的高维数据集Retail上的表现.为了能够做更好的说明,本次实验从现有的高维数据差分隐私发布方法中挑选了3个最具有代表性的方法来作为实验对比.这3个方法为降维系列方法中的PriView[17]方法、贝叶斯网络模型方法中的PrivBayes[19]方法、Markov网络模型方法中的Jtree[26]方法,它们都是目前比较最经典且权威的发布方法.以这3个方法作为实验对比,能够增加实验结果的可信程度.
我们将在Retail数据集上进行100次随机的重复实验,隐私预算ε分别设置为0.1和1.0.实验结果将通过200次随机的α-way查询进行验证,其中α的取值为4,6,8.实验结果如图5所示.
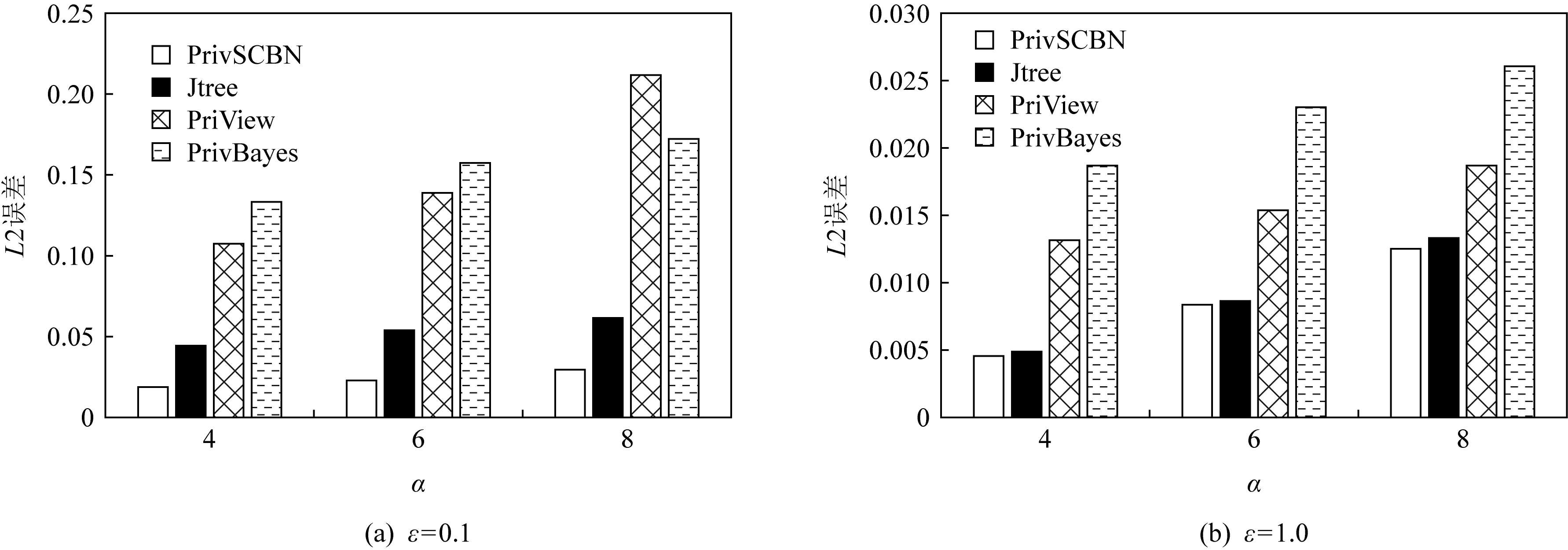
Fig. 5 Error analysis of α-way query in different methods on Retail dataset
从图5中可以看出,当隐私预算ε较小时(ε=0.1),PrivSCBN方法的表现要明显优于其他3种方法.而当隐私预算ε较大时(ε=1.0),PrivSCBN虽然仍优于其他3种方法,但与Jtree方法的结果相差不大.这是符合差分隐私规律的.因为随着隐私预算的不断增加,算法的隐私保护程度将会不断地下降,直至与无差分隐私保护算法的执行结果一致.因此,可以看出通过PrivSCBN方法构建的概率图模型本身的精度与用Jtree方法构建的模型精度相比,要来得更好一些.而与用PrivBayes方法构建的模型精度相比,要来得更好许多.这也进一步验证了本文提出的各种改进策略是有效的,并且取得了不错的效果.本次实验结果表明了PrivSCBN相较于其他3种方法具有更高的可用性.
5 结束语
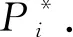
在未来的研究中,我们将进一步关注高维非二值数据的差分隐私发布问题,以及研究如何解决流式数据环境下的发布问题.
作者贡献声明:洪金鑫负责分析问题,设计算法,验证实验和撰写论文;吴英杰负责提出问题,参与算法讨论,指导论文写作;蔡剑平负责协助分析,参与算法讨论,指导论文写作;孙岚负责协助分析,参与算法讨论,指导论文写作.
