ESA：一种新型的隐私保护框架

王雷霞 孟小峰

(中国人民大学信息学院 北京 100872)

随着数据驱动的人工智能等技术的飞速发展，用户数据收集的需求越来越迫切.但随着隐私泄露事件的频发，用户隐私保障逐步成为各企业数据收集的“壁垒”[1-2].具体而言，近几年典型的隐私泄露事件包括Uber账户数据泄露事件、Facebook剑桥分析事件，造成了千万级的用户数据外泄或滥用[3].为严防此类事件的频发，各国政府都颁布了相关法令以对用户隐私数据进行法律意义上的保护.典型的，2016年4月，欧盟通过了《通用数据保护条例》(General Data Protection Regulation, GDPR)[4]，明确规定用户在数据上的查阅权、被遗忘权等权利；2019年5月，中国国家互联网信息办公室发布了《数据安全管理办法(征求意见稿)》[5]，以保障用户个人信息和重要数据在网络空间中的安全，并从数据收集、处理使用、安全监管3个方面讨论其办法.然而，数据的特殊性质决定用户的隐私问题不能仅通过法律法规界定其归属解决[6]，企业也不能因此放弃对用户敏感数据的收集，发展在大数据收集场景下兼顾数据隐私性与可用性的隐私保护技术势在必行.

隐私保护技术经过近20年的发展，已经有了诸多较为成熟的方法与体系[7]，典型的包括匿名化技术[8-11]、差分隐私技术[12-13]、密码学技术等.在大数据场景下，当前主流的隐私保护技术是差分隐私技术，更具体的指本地化差分隐私技术(local differential privacy, LDP)[14]，谷歌[15]、微软[16]和苹果[17]等企业都借助该技术完成特定的用户行为信息统计.差分隐私类方法本质上都是在保证数据整体分布不变的情况下对数据进行扰动，本地化差分隐私技术的优势主要体现在对隐私的严格定义和对数据收集场景的适用性上.具体地，在隐私定义上，它保证了任意一条用户数据的增、删、改都对用户发布数据的统计分布几乎无影响，可从根本上抵御匿名化方法难以应对的背景知识攻击；在场景适用性上，它直接在用户本地端对数据进行扰动，并只对外发布扰动数据以保护隐私，无需依赖任何第三方.但该方法也存在着致命的缺点，即在本地端添加过多噪声，使得数据的可用性较差.使用该方法，企业要么承受该数据误差，要么为提高数据可用性提高隐私损失ε，从而使得用户数据的隐私度降低.

从理想的角度出发，是否存在一种隐私保护方法在不对数据扰动的情况下保护隐私，使得数据的隐私性与可用性两者兼得?2017年谷歌的Bittau等人[18]提出ESA(encode-shuffle-analyze)框架，向该理想状态跨出有力的一步.该框架主要由编码器(encoder)、混洗器(shuffler)和分析器(analyzer)3部分组成：编码器运行在客户端，对用户数据进行本地化的编码、分割、扰动等处理；混洗器运行在一个半诚信的第三方，它可借助现有的安全混洗协议[19-25]在对数据一无所知的情况下完成安全的混洗操作；分析器运行在真正的数据收集者端，对收集的数据进行校正与分析.该框架中，混洗器完成了对用户数据完全匿名的操作，使得用户可以在尽可能对数据本身进行较小扰动的情况，获得较多的隐私保护.

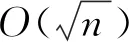
更具体地，图1对该例子中数据收集者获得频数估计的分布进行展示，基于ESA框架扰动后的结果更接近于原始数据，而本地化差分隐私方法扰动后的结果则与真实结果相距甚远.值得说明的是，基于ESA框架扰动后的结果与中心化差分隐私方法(central differential privacy, CDP)在该案例下获得的结果近似，但该中心化差分隐私方法假设数据收集者可信(或存在一个可信第三方)，是在对用户真实数据的计算结果(即直方图)上直接添加1次Laplace噪声得到的，而基于ESA框架的方法上需在用户本地添加总共n次噪声.

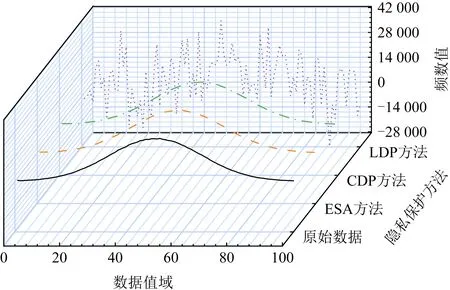
Fig. 1 Comparison of different methods’ results

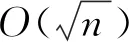
当前对ESA框架的研究仍处于起步阶段，以混洗差分隐私为主要方法，主要集中在2个方面：1)对其隐私增强效果的理论证明，即隐私放大(privacy amplification)理论；2)基于该模型提出不同统计估计方法.就混洗差分隐私而言，隐私放大理论是指用户在本地通过本地化差分隐私的方法对数据进行扰动，使得扰动后的数据经混洗实现接近于中心化方法所获得的数据统计结果.在不同统计估计方法实现时，可基于现有的差分隐私技术[31-32]进行设计，为了进一步提高准确性，也可借助密码学中Split-Mix方法[33]进行构建.

本文对该新型的隐私保护框架进行综述，主要贡献有4个方面：

1) 本文对ESA框架的实现机理与隐私保护程度进行详尽的分析，并以混洗差分隐私为例与其他差分隐私模型进行对比，以说明该框架的优势(第1节)；

2) 本文对ESA框架实现的主要方法——混洗差分隐私进行分析总结，包括该方法设计与实现的基础理论与技术(第2，3节)，以及该方法下具体的隐私保护机制(第4，5节).具体地，本文按研究问题分类，对混洗差分隐私的计数估计、频数估计、求和估计及其他的简单统计问题进行了对比分析.

3) 本文通过实验对混洗差分隐私下不同统计问题的隐私保护机制进行对比.当前绝大多数工作都是理论研究，本文通过实验对比，可以更直观地说明不同理论机制在实际应用时的效用和效率差异.

4) 基于对混洗差分隐私的理论与实验分析，本文提出ESA框架应用与发展的挑战问题，对本文进行总结.其中，考虑到混洗差分隐私在应用上固有的局限性、在方法设计中的明显不足，本文对ESA框架下的非差分隐私方法进行展望(第6，7节).

1 ESA隐私保护框架

之后，以当前主流的混洗差分隐私框架(即ESA框架与差分隐私的结合)为主要案例，在实现同样隐私目标的情况下，与传统的隐私保护框架对比，包括中心化差分隐私框架、本地化差分隐私框架及基于密码学的差分隐私框架.最终通过对比说明，ESA框架不仅有利于隐私保护中数据高隐私度与高可用性的实现，对当前各企业已部署的本地化差分隐私框架也极具适应性.

1.1 ESA框架定义

ESA框架如图2所示，主要由编码器、混洗器和分析器构成，并假设这三方是不可合谋的.

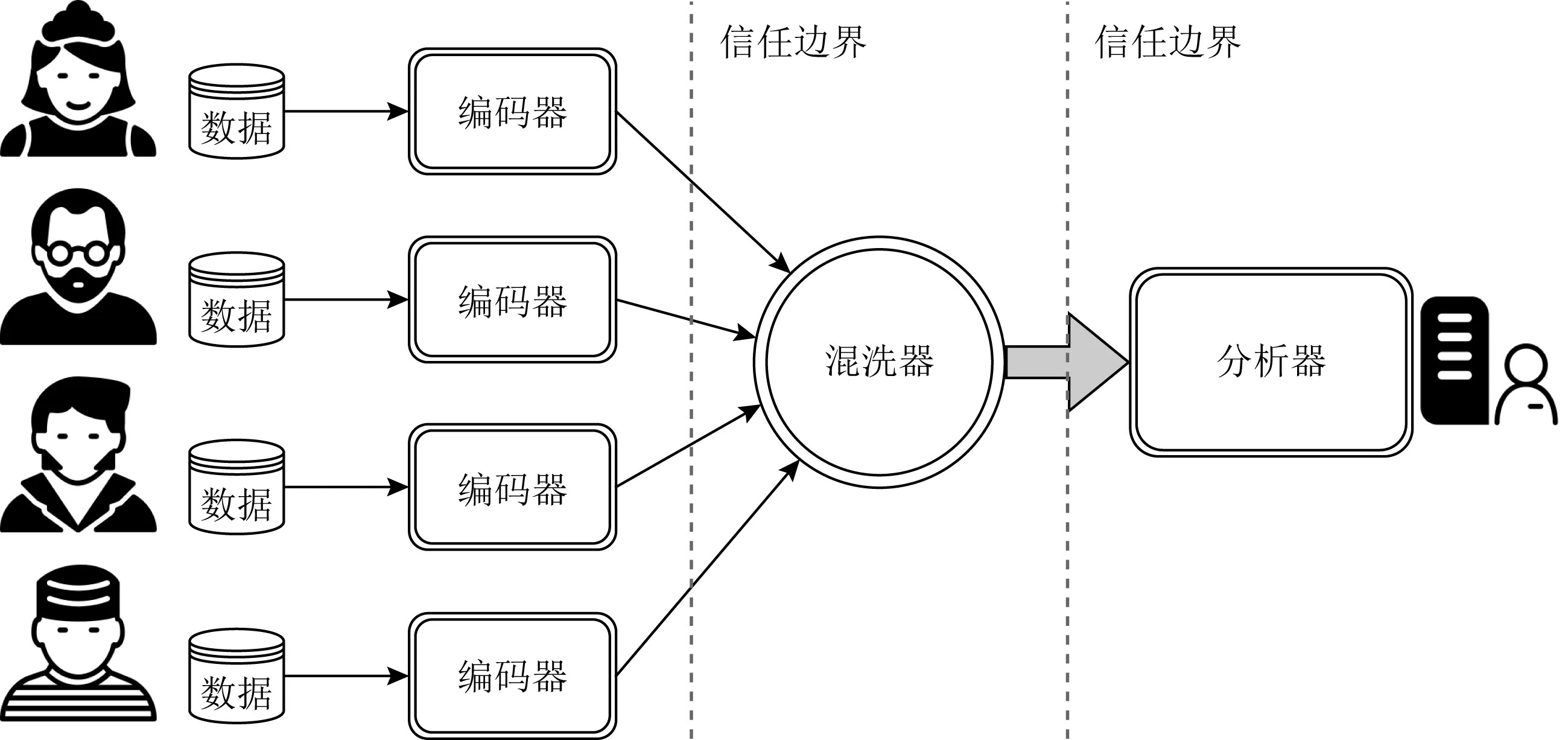
Fig. 2 ESA framework

① 半诚信参与方(semi-honest party)[36]，又称诚实且好奇的参与方(honest-but-curious party)，是源于密码学中的一个安全假设，假设该参与方会正确遵循协议的执行，但对计算的中间结果保持好奇，并依此进行推理攻击(inference attack).

1) 编码器.主要运行在用户的本地客户端，通常被认为是可信的.它的作用是对用户数据进行编码，以完成对用户数据的发布范围、粒度、扰动程度以及随机化程度的控制，在不依赖任何信任假设的情况下保护用户数据隐私[15].

编码器可根据其输出消息的多寡分为单消息模式和多消息模式[34-35].单消息模式指用户将数据编码为1条消息，形式上可以是1个数值、1个二元组或1个数组，每个消息都是后续处理的最小单元；多消息模式指用户将数据编码为多条可分别处理的消息，如多个数值、二元组和数组等.对于同一输入，通常情况下多消息模式可携带更多信息，有助于分析器获取更准确的分析结果.

编码器的具体实现，可通过数据泛化、数据分割、加密、添加差分隐私噪声的方式实现，以达到消除或减少数据所蕴含的隐私信息的目的[18].

2) 混洗器.是独立的半诚信(semi-honest)①服务器，可在对数据内容一无所知的情况下执行安全的混洗操作，是ESA框架的核心组件.它的作用是接收用户编码后的数据，消除相应的元数据(包括接收时间、顺序、IP地址等)，并对接收数据进行混洗(即打乱顺序)，以达到匿名目的.为保证足够的隐私保护效果，该混洗器需等待一段时间收集足够的用户数据进行混洗，并对数据量满足一定阈值的数据进行发布.当数据量为敏感信息时，可对该阈值添加满足差分隐私的噪声进行扰动，或者随机丢掉一些数据使数据量满足差分隐私[18]，从而保护数据量隐私.

在混洗器的模式上，可分为单混洗器模式和多混洗器模式[34-35].单混洗器模式是将所有编码器输出的数据一起混洗，即从逻辑上使用1个混洗器进行混洗；多混洗器模式是将编码器输出的数据按属性或其他特征进行分类，从逻辑上使用多个混洗器对每个分类内的数据分别进行混洗.多混洗器模式通常用于属性或分类特征不敏感的情况下，与多消息模式的编码器相结合.但多混洗器模式并不与编码器中的多消息模式对应，多消息的消息也可以使用单混洗模式的混洗器.单混洗模式将所有数据混淆，具有更高的隐私性；但对多消息的分类特征不敏感的情况，使用多混洗模式会获得更高的数据可用性.

混洗器的具体实现可根据该模型部署的条件借助已有的安全混洗协议[18-24]，基于可信硬件[25]、同态加密[36-38]或安全多方计算[39]等方式完成.特别地，单混洗模式和多混洗模式并不与混洗器具体实现的数量一一对应，这2个混洗模式是从隐私的逻辑层面进行定义的.多混洗模式可使用1个混洗器实现，即为每个分类添加标签，对属于不同标签的数据分别进行混洗；这2个混洗模式都可基于现有的安全协议使用多个混洗器实现，以避免单点失败.

3) 分析器.由数据收集者运行，是不可信服务器.它的作用是接收混洗器发布的数据，依据相应的编码和混洗规则对数据进行分析与校正，并获取最终的统计结果.该框架中数据的隐私性主要是针对分析器而言的，即将分析器视为数据的窥探者.

本文综述的重点在于如何设计编码器和分析器，选择恰当的混洗模式来进行满足一定隐私保证的统计计算.本文将混洗器作为黑盒来使用，假设其可以完成安全的混洗操作，主要原因是安全混洗协议已经发展成熟，在诸多安全相关的文献中已有过总结和论述[18-24]；同时安全混洗协议的不同实现并不会对该框架下隐私保护方法的隐私性和可用性造成明显影响.

1.2 ESA隐私分析

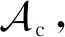
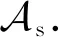
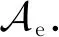
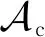
1.3 应用实例：混洗差分隐私方法

通常情况下，研究者们将ESA框架与隐私定义严格的差分隐私进行结合，即保证分析器所获得的最终输出满足差分隐私定义，以此来对数据隐私进行保证与度量.该结合被称为混洗差分隐私，如图3(b)所示，是本文所探讨的核心方法.

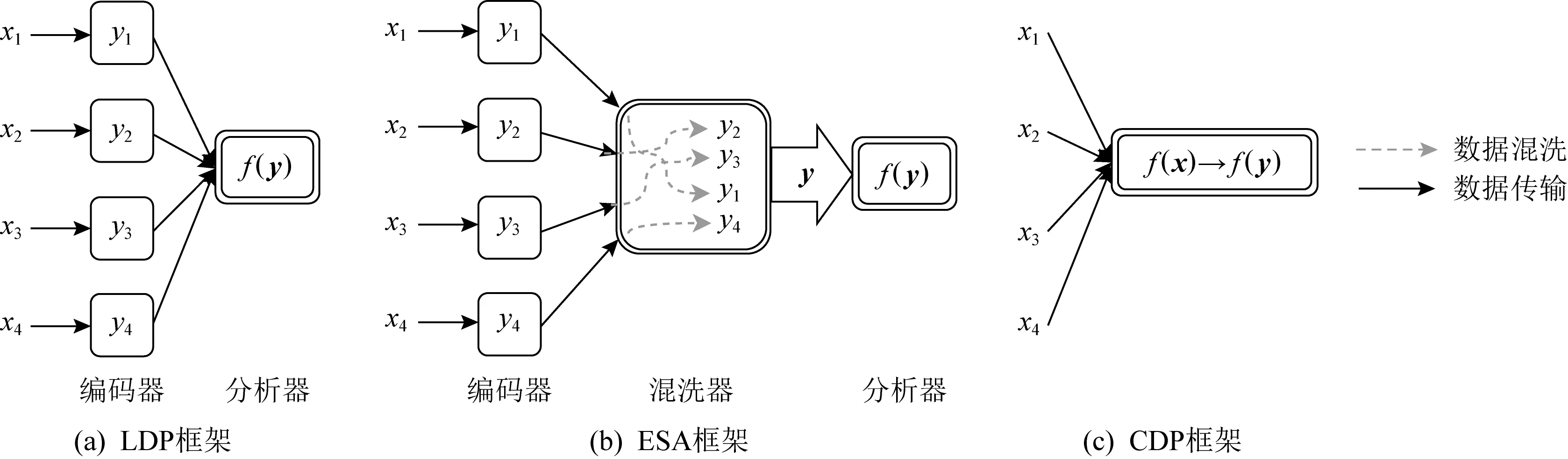
Fig. 3 Comparison of differential privacy methods under different frameworks

对发展历史已久的差分隐私方法而言，现存在着中心化差分隐私、本地化差分隐私、基于加密的差分隐私等多种基于不同隐私保护框架实现的差分隐私方法.本节将混洗差分隐私与其他差分隐私方法进行对比，以说明ESA框架在数据隐私性、数据可用性和框架易用性上的显著优势.

1.3.1 与中心化、本地化差分隐私对比

混洗差分隐私方法与本地化差分隐私方法具有高度的相似性，它们可使用相同的编码器，实现用户本地数据的差分隐私.混洗差分隐私方法可视为在本地差分隐私框架上增加混洗器得到的，该混洗器依赖于半诚信的安全假设，相比于无任何可信依赖的本地化差分隐私框架，其可信假设更强.但混洗器所完成的匿名操作，可有效实现隐私增强的效果，意味着在保证同样ε-差分隐私保护的前提下，混洗差分隐私框架可通过编码器添加较小的噪声来提高最终数据的可用性.

中心化差分隐私使用集中式隐私保护框架，将分析器和编码器集成在一起，放置于一个可信的第三方，该第三方可视为数据收集者.该方法中，数据收集者收集用户原始数据，在该数据上进行分析，之后发布添加差分隐私噪声的分析结果.混洗差分隐私方法与之相比，虽在用户数据上添加了较多噪声损失了一定数据的可用性，但摆脱了对可信服务器的强依赖.

总体而言，在模型对可信第三方的依赖程度上，本地化差分隐私<混洗差分隐私<中心化差分隐私，即本地化差分隐私拥有最小的可信假设；以同一ε-差分隐私为目的，在分析结果的可用性上，中心化差分隐私>混洗差分隐私>本地化差分隐私，即中心化差分隐私拥有最高的结果可用性.由此可发现，混洗差分隐私方法在隐私与可用性上，均介于本地化与中心化差分隐私两者之间，实现了更好的平衡.

1.3.2 与基于加密的差分隐私对比

仅从数据可用性的角度出发，基于加密的差分隐私也可在无需可信第三方支持的隐私保护框架上，实现可用性与中心化方法接近的差分隐私[41]，与混洗差分隐私方法的结果相似.如图4所示，在该框架中，用户需在本地端对数据进行同态加密，将加密后的数据发送给服务器.之后，服务器借助2个不可共谋的云，在加密数据上计算查询结果并添加满足差分隐私的噪声，发布该扰动的数据.

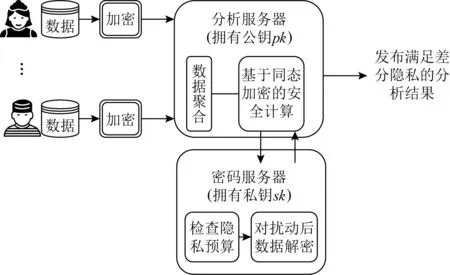
Fig. 4 Cryptographic differential privacy framework

但相比混洗差分隐私方法，该方法借助同态加密完成查询计算，会产生较高的计算代价和通信代价.同时，该框架需针对每一个查询特别设计隐私协议，而混洗差分隐私框架可通过简单的更改部署在现有的、广泛应用的本地化差分隐私框架上，具有较强的适应性.类似基于图4的加密差分隐私方法还有文献[42-43]，均具有上述不足.

综上，通过对不同框架下差分隐私方法的直观对比，说明了混洗差分隐私在隐私性、可用性和易用性上的突出优势，而这些优势均得益于ESA框架的应用与部署.后文，将对该混洗差分隐私方法进行详细的理论分析与实验对比，同时对ESA框架下其他隐私保护问题与方法的实现进行分析与展望.

2 基于ESA的隐私保护基础理论

本节以混洗差分隐私为主要方法，对ESA框架下隐私保护机制设计与实现的基础理论进行介绍.首先，本节对差分隐私的基本定义和重要性质进行回顾，之后，在ESA框架下基于差分隐私概念提出混洗差分隐私.最终，基于混洗差分隐私，本节给出ESA框架下隐私放大理论的严格定义与实验分析.该理论严格证明了混洗器对用户本地端隐私保证的增强效果，说明ESA框架可在本地添加较少噪声来实现较强的隐私保护效果，从而提高数据可用性.

2.1 差分隐私

Pr(M(D)∈S)≤eεPr(M(D′)∈S)+δ.

(1)

该定义为差分隐私的一般定义，也可将其视作中心化差分隐私的定义.相应地，本地化差分隐私考虑分布式数据集，即每个用户拥有1个数据，且数据收集者可将收集的数据和用户相关联.为保证数据收集者所收集的数据满足差分隐私，需保证每个用户的输出均满足差分隐私，因此得到如下本地化差分隐私的定义：

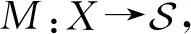
Pr(M(x)∈S)≤eεPr(M(x′)∈S)+δ.

(2)

在定义1和定义2中，当δ=0时，可得到纯差分隐私(pure differential privacy)的定义，可分别标记为ε-DP和ε-LDP；否则称为近似差分隐私(approximate differential privacy).ε被称为隐私代价或隐私预算，该值越小，说明相邻数据集或不同用户输入产生同一结果的概率越相近，该算法的隐私保护程度越高.δ表示相邻数据集输出结果存在概率δ使其不满足纯差分隐私，该值越小，该算法的隐私保护程度越高.

中心化与本地化的差分隐私均具有序列组合性(sequential composition)、并行组合性(parallel composition)和后处理性(post-processing)这样3条重要性质.差分隐私的组合性可帮助协议设计者进行隐私预算ε的分割，后处理性质对定义在ESA框架上的差分隐私十分关键.

性质1.序列组合性[45].给定数据集D和m个随机化算法{M1,M2,…,Mm}，算法Mi，1≤i≤m满足εi-DP，则这m个Mi(D)算法构成的序列满足∑εi-DP.

性质2.并行组合性[45].给定数据集D={D1∪D2∪…∪Dm}，其中Di，1≤i≤m和Dj，1≤j≤m且i≠j为互不相交的数据集，设Mi满足εi-DP的算法，则这m个Mi(Di)算法构成的序列满足max{εi}-DP.

性质3.后处理性[46].给定满足(ε,δ)-DP的随机化算法M，令f为任意的随机化函数，则f∘M依旧满足(ε,δ)-DP.

序列组合性说明隐私预算ε可以在算法设计的不同步骤进行分配；并行组合性则定义了算法在不相交数据集上的隐私保证；后处理性则强调，在满足ε-DP的数据结果上进行随机操作，其输出依旧满足ε-DP.这3条性质适用于本地化差分隐私时，数据集D相应地定义在用户本地的数据集上.

2.2 混洗差分隐私

基于定义1～2与性质1～3，结合ESA框架，本节给出混洗差分隐私的定义.简单而言，混洗差分隐私要求对分析器来说，其收集的数据满足定义1中差分隐私的要求.同时，差分隐私的后处理性说明，只要ESA框架中的随机化编码器R和混洗器S处理过后的数据满足差分隐私，最终结果即满足差分隐私.该结果的隐私效果与分析器无关，分析器的重要作用是对扰动数据进行计算，对估计结果进行校正.

定义3.混洗差分隐私[47].给定n个可信用户，每个用户对应1条记录xi.令R:X→Ym表示随机化的编码器，其中m表示编码后消息的数量；S:Ym→Π(Ym)表示混洗操作；算法A:Π(Ym)→Z为分析函数，其中Π表示乱序，则混洗差分隐私协议可表示为P=(R,S,A).根据后处理性，则协议P满足(ε,δ)-DP,当且仅当扰动后的数据S∘Rn=S(R(x1),R(x2),…,R(xn))=Π(R(x1),R(x2),…,R(xn))满足(ε,δ)-DP.

定义3假设参与计算的用户都是可信的，即都会按照协议正确地参与计算.但如果存在用户不可信、掉线或者与分析器共谋，则会大大影响混洗的效果，从而影响最终的差分隐私效果，由此，具有鲁棒性的混洗差分隐私被提出.

定义4.具有鲁棒性的混洗差分隐私(robust shuffle differential privacy, RSDP)[48].给定N个用户和可信用户比例γ∈(0,1]，如果对于所有的N∈+，γ′>γ，算法S∘Rγ′N满足(ε,δ)-DP，则混洗差分隐私协议P=(R,S,A)满足(ε,δ,γ)-RSDP.

定义4保证了，在至少有γ比例的用户正确遵循协议的情况下，混洗差分隐私协议P满足(ε,δ)-DP.特别说明，此处的鲁棒性是对隐私性的保证，而非算法可用性的保证.

2.3 隐私放大理论

隐私放大(privacy amplification)是ESA框架中混洗器对隐私效果增强的理论分析，基于该理论，可将现有的本地化差分隐私方法直接应用在ESA框架上.具体地，在混洗差分隐私框架中，假设用户在本地端通过随机编码器R扰动后的数据满足εl-LDP，经过混洗后，分析器所获取的数据满足εc-DP，从εl到εc的转变可通过隐私放大理论获取.εl对应于较大的数值，表示较低的隐私性；εc对应于较小的数值，表示较高的隐私性.针对具体的差分隐私机制，研究者们提出了不同的隐私放大定理.

2.3.1 通用隐私放大定理

与差分隐私相同，混洗差分隐私也存在交互式和非交互式2种隐私保护机制[49-50]，如图5所示.假设存在n个可信用户，每个用户拥有输入xi和相同的随机化的编码协议Ri，在交互机制中，协议Ri的输入为{R1(x1),R2(x2),…,Ri-1(xi-1),xi}，即与前i-1个编码器结果和用户的输入xi相关；而非交互机制中协议Ri仅与用户的输入xi有关，可视为交互机制的简化.

交互机制可以处理较为复杂的、用户间有关联关系的统计分析，如果一些遗传病的统计，被统计者与其亲属可能存在关联关系；而非交互机制仅可以处理用户数据独立的统计分析.相应地，基于这2种机制，研究者们提出了2个通用隐私放大定理.

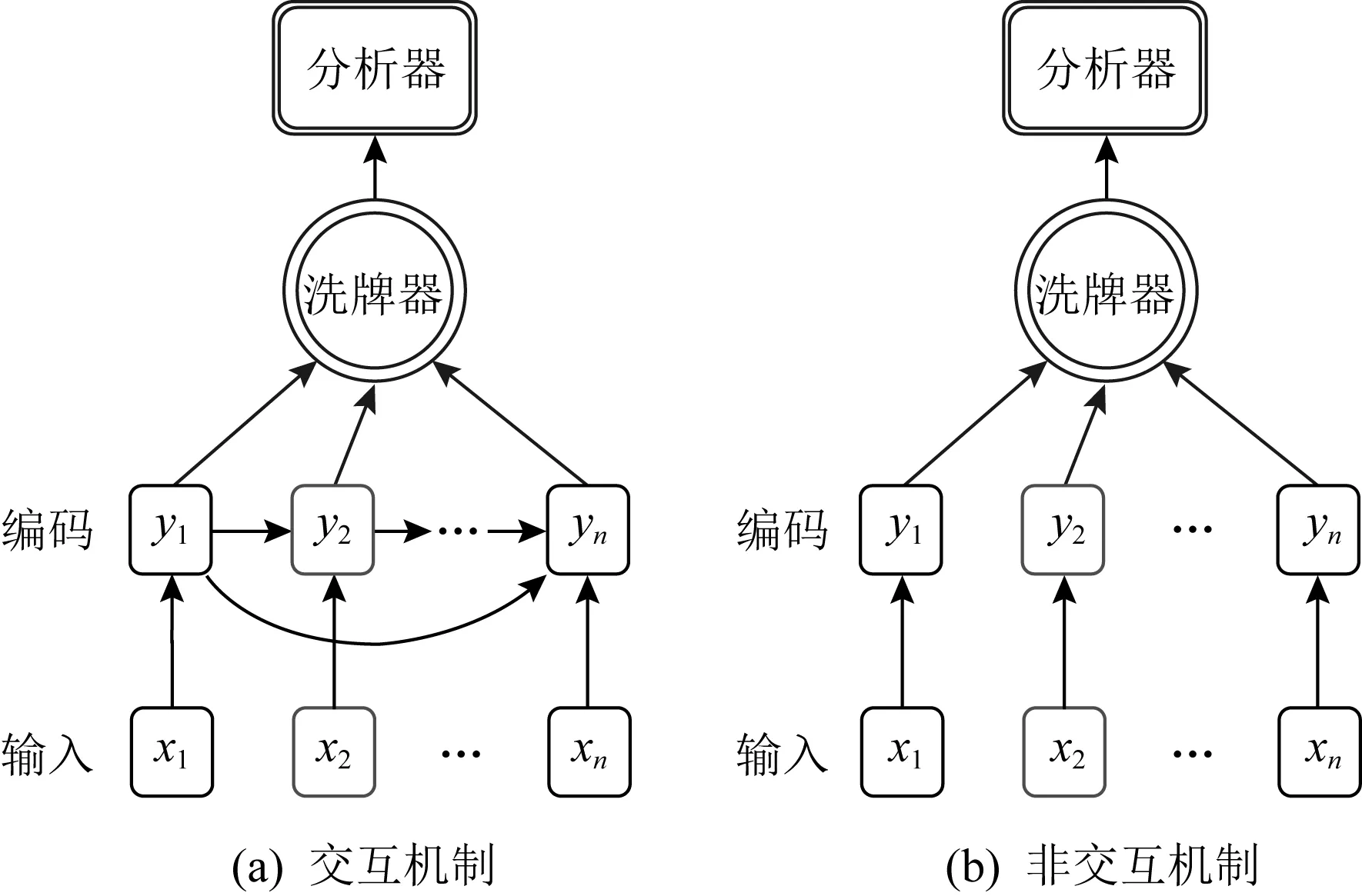
Fig. 5 Interactive mechanism and non-interactive mechanism

定理1.通用交互机制的隐私放大定理[26].给定n个用户，每个用户对应1条记录xi，且在本地运行随机化编码协议R.对于任意的n>1 000，δ∈(0,0.01)，如果协议R满足εl-本地化差分隐私，且εl∈(0,0.5)，则协议S∘Rn对应混洗后的n个输出满足(εc,δ)-DP，其中

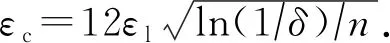
(3)

定理2.通用非交互机制的隐私放大定理[47].给定n个用户，每个用户对应1条记录xi，且在本地运行随机化编码协议R.对于任意的n∈+，δ∈[0,1]，εl∈(0,ln(n/ln(1/δ))/2]，如果协议R满足εl-LDP，则协议S∘Rn对应混洗后的n个输出满足(εc,δ)-DP，其中

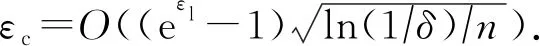
(4)

根据定理1和定理2，设定δ=10-9，可得到表1和表2中隐私放大结果.令n表示参与计算的可信用户数量，表1为根据式(3)计算εl经隐私放大后得到的εc取值；表2为根据式(4)计算εc对应的被放大前的εl取值.根据表1和表2可发现，通过隐私放大，可轻易实现在用户本地端添加满足较大εl-LDP的噪声，而在分析器端获得较小的εc-DP保证.同时，隐私放大效果随着参与用户数量的增加而增大.

Table 1 Results of Privacy Amplification on General Interactive Mechanism

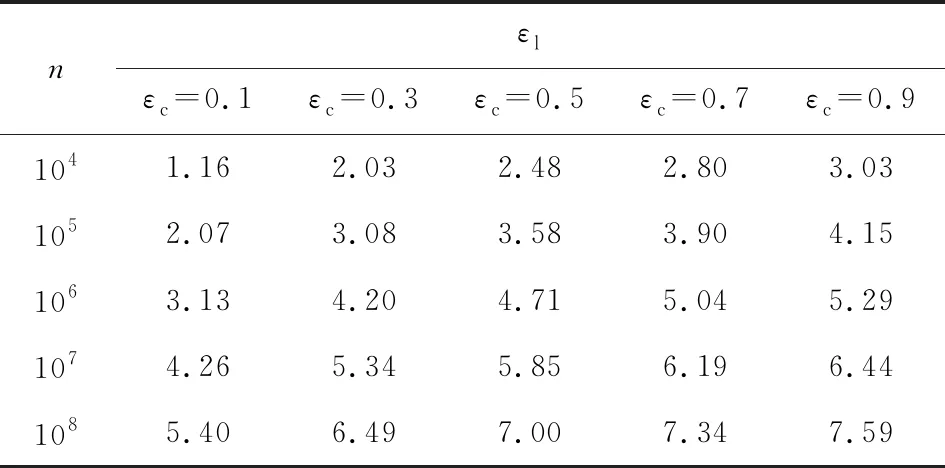
Table 2 Converse Results of Privacy Amplification on General Non-interactive Mechanism

通过表1中的分析计算可发现，通用交互机制的隐私放大结果是不适用于现实情况的.由于该机制仅在εl∈(0,0.5)时生效，此时εc的取值往往小于0.2.现实情况中，通常并不需要如此严格的(如此小的εc)差分隐私保证，并且用户端添加过小的εl，会给统计结果造成较大误差.由此，通用非交互机制的隐私放大定理往往会有更多的应用.

2.3.2 基于随机响应的隐私放大定理

为了获取更好的隐私放大的效果，研究者们针对具体的差分隐私机制提出了更精确的隐私放大定理.被应用最多的，是基于随机响应机制提出的隐私放大定理.随机响应机制是本地化差分隐私的基本扰动技术，Warner[51]于1965年提出.为方便后续应用，本节对该机制进行一定程度的扩展，并描述如下[27,47].

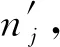
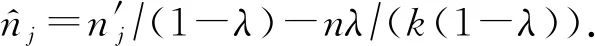
(5)

当k=2时，假设v1=‘Yes’，v2=‘No’，则上述机制即为经典的随机响应机制，回答“Yes/No”的问题，本文将其称为布尔随机响应机制(Boolean random response mechanism).当k≥2时，本文将其称为k值随机响应机制(k-random response mech-anism,kRR).之所以将其区分开，是由于在进行复杂差分隐私机制设计时，通常要考虑对数据01编码或直接使用该数值的问题，涉及上述2种不同方案.基于此，研究者们提出了2种相应的隐私放大定理.

定理3.布尔随机响应机制的隐私放大定理[28].给定n个用户，每个用户对应1条记录xi∈{0,1}，且在本地运行协议R.对于任意的n∈+，δ∈[0,1]，λ∈[14 ln(4/δ)/n,1]，如果协议R以λ的概率均匀输出{0,1}中的值，1-λ的概率输出真实值，则协议S∘Rn对应混洗后的n个输出满足(εc,δ)-DP，其中

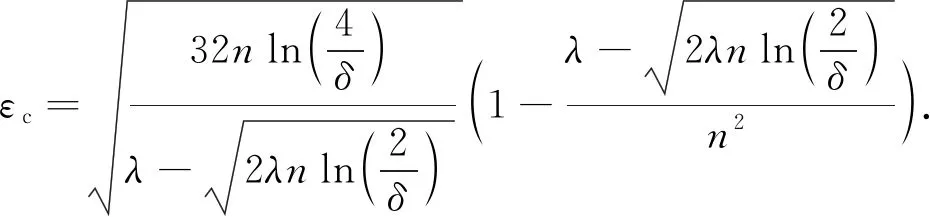
(6)

在定理3中，当λ=2/(eεl+1)时，布尔随机响应机制满足εl-LDP.将该式代入式(6)，通过简化，可得到宽松的隐私放大效果[52],即当0<εl≤lnn-ln(14 ln(4/δ))时，

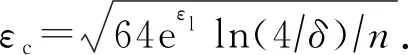
(7)

定理4.k值随机响应机制的隐私放大定理[47].给定n个用户，每个用户对应1条记录xi∈{1,2,…,k}，且在本地运行协议R.对于任意的k,n∈+，λ∈[0,1]，εc∈(0,1]，如果协议R以λ的概率均匀输出{1,2,…,k}中的值，以1-λ的概率输出真实值，则当λ满足式(8)时，协议S∘Rn对应混洗后的n个输出满足(εc,δ)-DP.

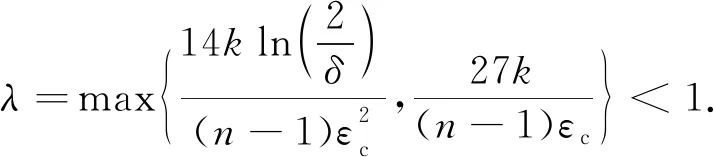
(8)

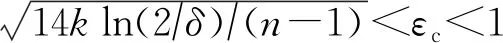
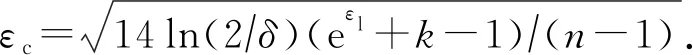
(9)

与2.3.1节相同，设定δ=10-9，针对不同的可信用户数量n，表3表示根据定理3在给定n和εc的情况下，计算εl的取值情况；表4表示根据定理4，在给定n，εc，并假设k=2的情况下，计算εl的取值情况.在表3(表4)的结果中，None表示εl的取值不满足定理3(定理4)，无法进行隐私放大.

显然，在针对2个离散值进行扰动时，定理4的隐私放大效果优于定理3，由此选用定理4进行基于随机响应机制的隐私放大是更明智的选择.同时通过分析发现，随着k值的增大，定理4的隐私放大效果会缩减，但并不明显.通过实验发现，在给定n和εc的情况下，不同k值所造成隐私放大逆向计算结果εl的差异仅在小数点后几位体现.由于该计算结果较为简单，此处不予以展示.

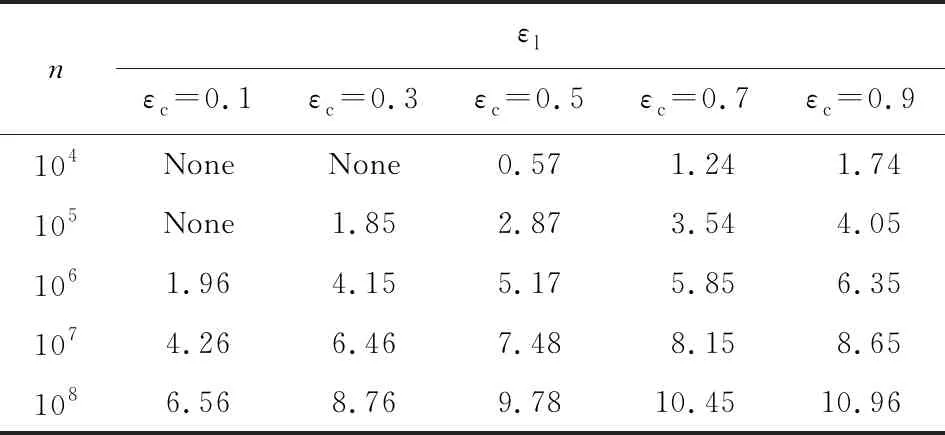
Table 3 Converse Results of Privacy Amplification on Boolean Random Response Mechanism

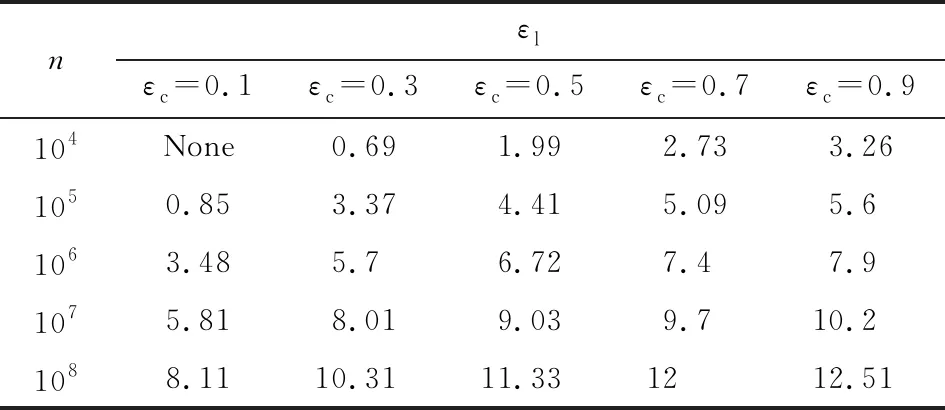
Table 4 Converse Results of Privacy Amplification on k Random Response Mechanism

3 基于ESA的隐私保护基础技术

本节以混洗差分隐私作为ESA实现的主要方案，对该方案构建的基础技术进行总结与介绍，为后文不同隐私保护方法的对比分析奠定基础.

这些基础技术主要分为2类：一类是差分隐私技术，包括中心化差分隐私、分布式差分隐私和本地化差分隐私中的具体隐私保护机制；另一类是基于匿名的密码学技术，具体指Split-Mix方法.差分隐私技术中，本地化差分隐私技术可与2.3节所述的隐私放大定理相结合以实现混洗差分隐私，该途径所获得的差分隐私模型较为简洁.基于匿名的密码学技术Split-Mix方法通常与中心化或分布式的差分隐私技术相结合以满足最终的差分隐私保证，在该过程中Split-Mix方法可进一步减少在原始数据中添加的噪声，使计数结果具有较高的准确性，但同时也会产生较高的通信代价.

3.1 差分隐私技术

差分隐私技术根据不同的使用场景，可分为中心化差分隐私、分布式差分隐私和本地化差分隐私3种，均可通过与ESA框架不同的结合方式实现混洗差分隐私，具体技术如下.

3.1.1 中心化差分隐私技术

中心化差分隐私技术指一般的差分隐私机制，该机制通常在统计分析结果(如直方图)上添加满足一定分布的噪声，使该扰动后的结果满足(ε,δ)-DP，以响应用户查询.为保证扰动后结果的无偏性，通常需要保证添加噪声的期望为0.常用差分隐私机制如下：

定理5.拉普拉斯机制[46].令f:Xn→是一个敏感度为Δ的函数，即对所有的相邻数据集D,D′∈Xn，|f(D)-f(D′)|≤Δ.当ε>0时，生成噪声η～Lap(Δ/ε)，则添加噪声后的输出f(D)+η满足ε-DP.

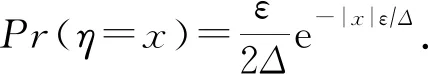
定理6.二项分布机制[53].令f:Xn→是一个敏感度为Δ的函数，即对所有的相邻数据集D,D′∈Xn，|f(D)-f(D′)|≤Δ.当ε>0，δ∈(0,1)，λ≥20(eε/Δ+1)/(eε/Δ-1)2ln(2/δ)时，生成噪声则添加噪声后的输出f(D)+η满足(ε,δ)-DP.

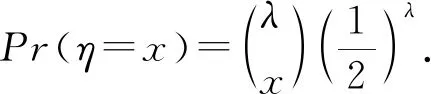
定理7.几何分布机制[54].令f:Xn→是一个敏感度为Δ的函数，即对所有相邻数据集D,D′∈Xn，|f(D)-f(D′)|≤Δ.当ε>0时，生成噪声η～SG(ε)，添加噪声后的输出f(D)+η满足ε-DP.

其中，SG(ε)表示对称几何分布，它对应的概率分布函数为Pr(η=x)=e-ε|x|/Δ×(eε/Δ-1)/(eε/Δ+1).该分布可看作离散化的拉普拉斯分布，其期望为0.该机制通常为整数数值添加噪声.

3.1.2 分布式差分隐私技术

分布式差分隐私技术与中心化差分隐私技术不同的是，该方法不直接在统计结果上添加噪声，而在用户端的原始数据上独立添加满足一定分布的随机噪声，并使得扰动后的数据在服务器端满足差分隐私.分布式差分隐私技术通常利用拉普拉斯分布无限可分性质，在用户端独立添加满足一定分布的噪声，使得在服务器端这些噪声的和满足拉普拉斯分布[31].

定理8.分布式几何分布机制[32,55].令n为可信用户数量,f:Xn→是一个敏感度为Δ的函数，即对所有的相邻数据集D,D′∈Xn，|f(D)-f(D′)|≤Δ，独立随机变量满足分布Pólya(1/n,e-ε/Δ)，则噪声η～SG(ε)可通过式(10)模拟：

(10)

3.1.3 本地化差分隐私技术

本地化差分隐私技术在用户端的原始数据上添加噪声，并保证任一用户的发布数据均满足差分隐私定义.该技术中最常用的是随机响应机制，亦可基于一般的差分隐私机制(指中心化差分隐私技术)实现，但会产生较多噪声.该技术是混洗差分隐私方法设计中最常用的基础技术，它结合混洗器的隐私放大效果可达到较强的差分隐私保护效果.

具体技术中，为了在随机响应机制的基础上进一步降低通信代价和均方误差，使计算结果不依赖于用户数据的值域，基于略图的本地化差分隐私(sketch-based local differential privacy)算法[56-57]被提出，即首先使用散列函数对用户数据进行映射，对该映射后的值进行扰动.Wang等人[57]针对此类方法以均方误差为目标函数对该最小值问题进行求解，提出了OLH方法，可在值域较大的情况下，实现与值域[d]大小无关的最优误差，[d]表示{1,2,…,d}.该方法将较大的数据值域[d]通过散列函数进行压缩，映射至较小的值域[d′]，用户将其拥有的值先用该散列函数进行散列，而后进行随机扰动，即以εl/(εl+d′-1)的概率保持该值不变，以1/(εl+d′-1)的概率扰动为值域{1,2,…,d′}内的其他值.当d′=eεl+1时，可使结果对应的均方误差最小.较大值域[d]指的是d≥3eεl+2时，否则应用通用的k值随机响应算法即可获得较小的均方误差.更多本地化差分隐私方法在文献[14]中已有详细综述，本节不再赘述.

3.2 基于匿名的密码学技术

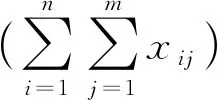
ESA框架中的混洗器相当于完成了彻底的匿名操作，由此可基于Split-Mix方法设计实现满足分析器端差分隐私的算法.同时，利用Split-Mix方法中类似秘密共享的操作，可进一步对用户端编码后的数据提供保护，分析器将会看到几乎完全随机的数据分片，如此可进一步减小差分隐私噪声的添加.Split-Mix方法与加法秘密共享不同的是，后者需保证不同的数据分片(即shares)由不同的参与者拥有，而该算法对数据分割获得的数据分片可由1个或多个混洗器持有，取决于混洗器的实现方式.

Ghazi等人首次提出并证明使用该算法可以在ESA框架中实现差分隐私[58]，并证明了该算法的误差上界，以及一轮协议(one-round protocol)下的误差下界[59].Balle等人[60]给出了与Split-Mix方法结合的差分隐私保证，见定理9.基于定理9，可以进一步设计出多消息模式下的混洗差分隐私机制.

定理9.假设算法M和算法M′的统计距离(总体方差)为μ(σ)，算法M满足(ε,δ)-DP，则算法M′满足(ε,δ+(1+eε)μ(σ))-DP.

4 基于ESA的隐私保护方法对比

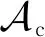
Table 5 Research Fields of Shuffle Differential Privacy

其中，计数估计、频数估计和求和估计是统计估计的基础问题，受到广泛关注，也是本节分析的重点.在本节的理论分析中，一般假设有n个用户参与计算，实现了分析器端(εc,δ)-DP的隐私保护效果.部分机制假设参与计算的用户不完全可信，此时使用的N表示用户数量，γ表示可信用户比例，可在分析器端实现具有鲁棒性的(ε,δ,γ)-RSDP；当γ=1时，它等同于(εc,δ)-DP.同时，在文中使用[d]表示{1,2,…,d}，[n]表示{1,2,…,n}.在不同估计机制的对比表中，通信代价指每个用户发送消息的数量，“—”表示该项隐私未得到严格的理论保证.

4.1 计数估计

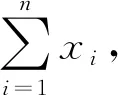
针对该问题，研究者们提出了若干方法，分别实现了不同的隐私目标.Cnt_RR[28]基于隐私放大理论，可实现不同ε的中心端差分隐私和本地端差分隐私.Cnt_2M[61]，Cnt_PURE[62]，Cnt_SGM[48]，Cnt_BN[48]仅考虑中心端差分隐私，其中，Cnt_2M实现近似差分隐私，Cnt_PURE实现纯差分隐私，Cnt_SGM和Cnt_BN则进一步考虑了用户不完全可信的场景，分别实现了分析器端具有鲁棒性的纯差分隐私和近似差分隐私.具体方法对比见表6，方法分析为：

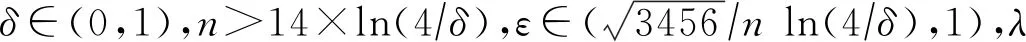
(11)

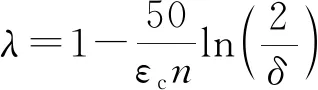
Table 6 Comparison of Counting Estimation Methods on Shuffle Differential Privacy

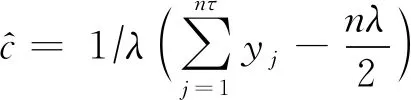
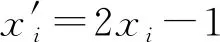
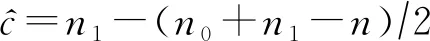
4.2 频数估计

频数估计中假设每个用户拥有1个离散型的值xi∈[d]，分析器端基于匿名的用户扰动数据估计这些数值频数count(j),j∈[d]，即估计用户数据的直方图.

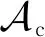
Table 7 Comparison of Frequency Estimation on Shuffle Differential Privacy

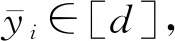
为了在值域[d]较大时进一步减少频数估计的误差，研究者们相继提出了若干频数估计方案，可实现与值域[d]无关的误差边界.

Hist_MM[61]方法基于计数机制Cnt_2M构建，仅考虑分析器端的差分隐私，不考虑用户端的差分隐私，由此无需根据值域[d]对用户端的隐私预算进行划分，分析器也可计算得到与[d]无关的误差边界.在该方法中，每个用户将其拥有的数据进行独热(one-hot)编码，即生成1个d长的向量，第xi位为1，其余位为0.之后对每一位{0,1}分别使用满足(εc/2,δ/2)-DP的Cnt_2M中的扰动机制进行扰动，得到yij={1}*.为了使得分析器能够在彻底的混洗后依然识别yij对应于哪一个离散值，用户将j×yij发送给混洗器进行扰动.最终分析器分别统计每一个值j∈[d]的计数，使用Cnt_2M中的校正机制进行校正，计算其频数.该机制的优点在于它的误差边界并不依赖于值域[d],但该机制所获得的估计结果是有偏的，且仅考虑了分析器作为攻击者时的隐私保护，不能保证对任意攻击者的用户端隐私.

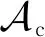
SLH机制使用1个混洗器进行混洗，一旦该混洗器与分析器串通，用户的隐私将不能得到保证.为了解决该问题，Wang等人[40]在SLH方法的基础上进一步提出了一个通用协议MURS(multi uniform random shufflers)，使用m个混洗器对用户数据进行混洗，每个混洗器在混洗的过程中都随机添加一些均匀分布的假数据.此处的多个混洗器完成的是几乎相同的工作，仍对应于1.1节中介绍的单混洗器模式，只是使用多个服务器来实现该模式.这样一来，即使有m-1个混洗器和除被攻击用户外其余n-1个用户都与分析器合谋，用户数据至少能得到由1个混洗器所添加的假数据构成的“隐私毯子”带来的保护.

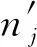
分析器端满足(εc,δ)-DP.

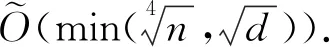
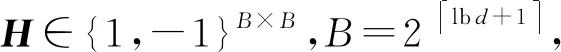
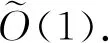
至此，上述分析的所有方法均针对单值频数估计，对于多值频数估计(即用户拥有多个值的情况)，通常情况下，可通过对隐私预算εc进行分割，或从多值中随机采样1个值进行扰动，文献[65-66]证明后者的误差更小.而针对ESA模型下的多值频数估计，Erlingsson等人[52]提出了“属性分段”(attribute fragmenting)的通用方法.对于一些独立的自然属性，如统计人群的年龄、性别等，可将不同的属性作为单独的分段分别扰动，每个属性使用1个单独的混洗器进行混洗，以提高数据可用性；对于非自然属性，可人为将其拆分为多个分段，应用该属性分段技术.该属性分段的应用特例是，对于用户拥有的数值xi可进行独热编码，而后使用Cnt_RR方法对每一比特位的数据分别进行扰动与混洗.

4.3 求和估计

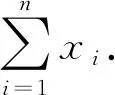
研究者们基于上述针对离散值的扰动方法(包括计数估计方法和频数估计方法)，提出了若干实数求和估计机制，如RSum_RR，RSum_KR，RSum_RM，RSum_DSG，RSum_PURE，其中RSum_PURE实现了纯差分隐私，其余均实现了近似差分隐私.每一个方法的提出，都相比前一个方法降低了统计结果的误差边界；但兼顾结果可用性和方法通信代价，RSum_RM应是当前可行性较高的估计方法.

在具体实现时，为了应用上述对离散值扰动的方法，首先需要将该实数根据一定规则编码为若干整数.通常情况下，研究者们会依据一定的准确度p将实数值xi其放大p倍得到pxi，而后将其无偏映射为离散型的整数，该过程称为随机舍入(random rounding).最终，在若干离散型数据上，基于布尔求和或频数估计方法进行计算.通常随机舍入算法需保证无偏，以保证最终结果的可用性.求和估计的方法对比见表8，具体方案如下所述.

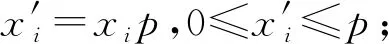
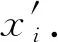
实数求和估计结果的准确性一方面依赖于隐私预算εc的分配与方法的隐私放大效果；另一方面也与随机舍入的结果的准确性有关.进一步地，RSum_RM[35]方法将用户拥有的xi∈[0,1]随机舍入为多个更为准确的值，以提高方法的可用性.

RSum_RM[35]方法的核心思想是，通过将用户拥有的数值xi∈[0,1]依据m个固定的准确度编码为多个值，并对编码后的值分别独立地应用随机响应方法，从而尽可能利用混洗器提供的隐私保护.具体地，给定一系列准确度p1,p2,…,pm∈+，令则

其中

Table 8 Comparison of Sum Estimation on Shuffle Differential Privacy

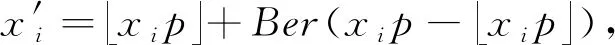
虽然RSum_DSG方法从理论上获得了与n无关的均方误差MSE，但该方法的通信代价过大.通常情况下，选择方法RSum_RM更具实用性，用户可根据其带宽选择多消息模式编码器中消息的数量m，当m=2或3时，即可取得可用性相对较好的结果.

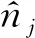
4.4 其他统计问题

除了基本的计数估计和频数估计，研究者们还关注了其他相对复杂的统计和查询问题，包括不同元素计数(distinct elements counting)、范围计数和均匀性检验，具体可见表7.本节对这些方法进行理论分析与总结，由于这些方法均使用了多消息模式和单洗牌器模式，不再将这2项罗列在对比的表格当中.

4.4.1 不同元素计数

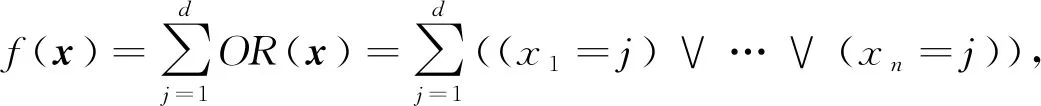
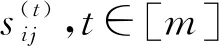
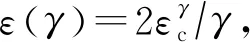
4.4.2 范围计数

给定数据的值域[d]，每个用户拥有1个xi∈[d],该问题统计在范围[j,j′]内值的计数，也就是取范围[j,j′]对应的直方图.令Y=hist(X)表示用户数据的直方图统计，w∈{0,1}d为该范围的编码表示，其中1≤j≤j′≤d，wj=wj+1=…=wj′=1，其余项为0，则范围计数的结果可以用[w,Y]表示，[·,·]表示点积.

Ghazi等人在文献[64]通过矩阵机制[67-68]将该范围计数问题归约为频数估计问题.根据矩阵机制，对于给定的数据集X，可基于可逆矩阵M∈{0,1}d×d，构造噪声扰动的直方图Y+ΔM-1ψ，Δ表示敏感度，即M中列的最大1范数，z表示随机的噪声向量.扰动后范围计数的结果[w,Y+ΔM-1ψ]等同于[wM-1,MY+Δψ]，令表示正常的频数估计方法扰动后的结果，由此范围计数可通过频数估计问题得到.基于该归约，用户可根据其拥有的数据xi，选择矩阵M中第xi列非0项对应的索引值j∈[d]作为其编码，并调用之前任一频数估计方法分别对每一个值进行扰动并输出；分析器收到混洗后的用户数据，首先估计频数之后通过即可返回范围计数的结果.

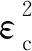
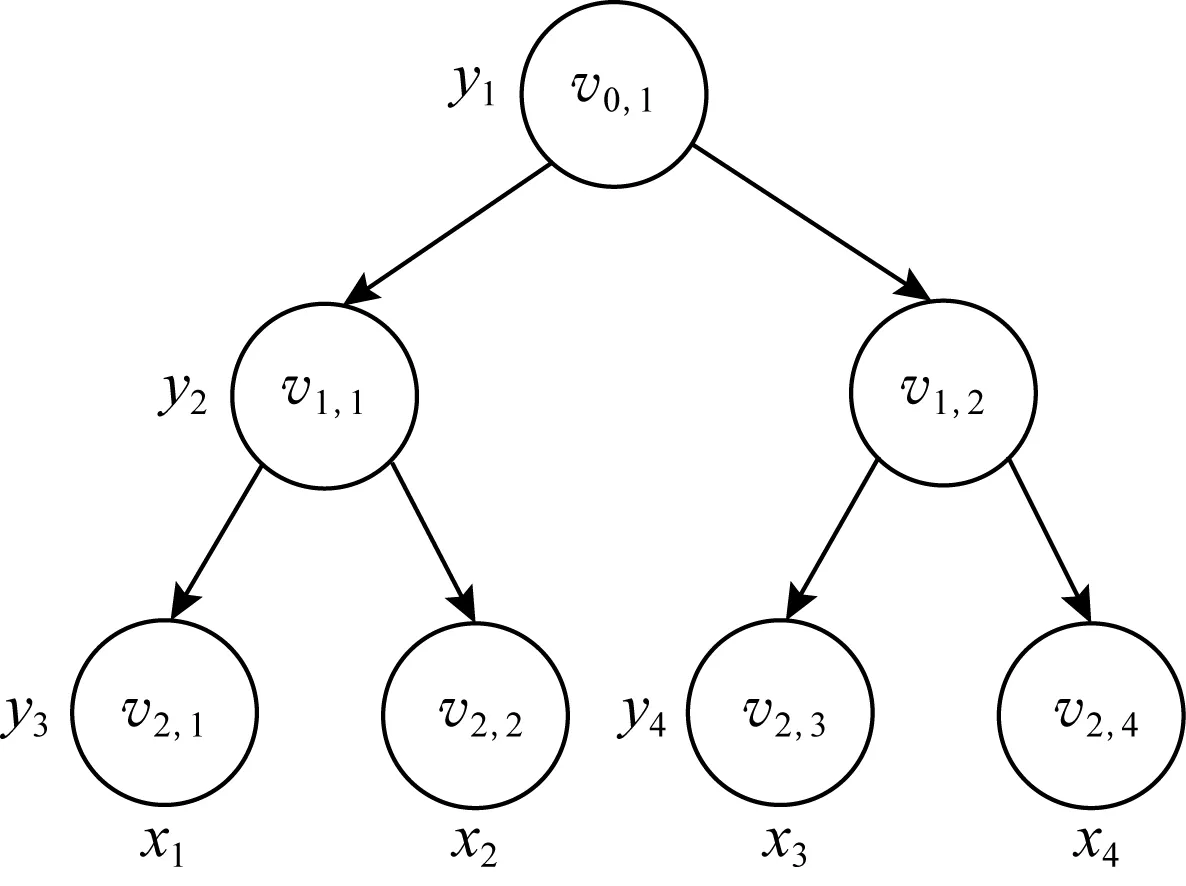
Fig. 6 Range query tree(d=4)

Table 9 Summary of Other Statistic Estimation on Shuffle Differential Privacy

4.4.3 均匀性检验

均匀性检验是指对于1个在值域[d]上的未知分布，检验该分布是否是均匀分布.下述用于均匀性检验的2个方法，均满足具有鲁棒性的差分隐私.

AUT[48]实现了具有鲁棒性的近似差分隐私.该方法的编码和扰动过程与PUT方法相似，将应用于编码后每一位的Cnt_SGM方法替换为Cnt_BN方法即可.与其他问题不同的是，在表9中，这2个方法的误差用样本复杂度来度量.

5 实验评估

基于ESA的隐私保护方法对比中，计数估计、求和估计和频数估计作为重点的基础问题，存在着若干种隐私保护方法.本节将这些方法进行了实现，并对其中的重要参数进行实验评估，对于本节未提及的参数，使用该方法在获得最优边界时的参数设定.该实验一方面评估部分参数对分析结果的影响，另一方面使同一问题下不同方法的对比更加直观.

本节的实验环境为Ubuntu系统，2个6核1.70 GHz的Intel®Xeon®CPU，94 GB内存.本节所使用的数据集为不同分布的人工合成数据集，此类数据集易于调整参数，以便观察不同分布数据集对不同方法结果的影响.该实验的参数设置中，所有实验都给定同一个εc，满足近似差分隐私的方法给定δ=10-6，使它们尽可能在同一隐私保护程度下进行对比.

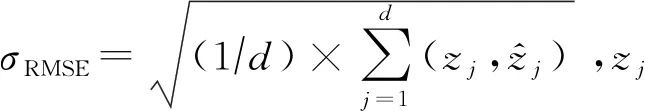
5.1 计数估计实验评估

该节通过人工生成n项满足伯努利分布Ber(q)的{0,1}数据作为数据集，并假设每个用户拥有其中1个数值，对计数估计问题中的Cnt_RR，Cnt_2M，Cnt_SGM，Cnt_BN方法进行实验评估.此处没有对Cnt_PURE进行评估，主要原因是根据其理论，该方法仅对n较大且ε较小的情况下适用，很难与其他方法放在同一标尺下度量.如当n=107时，εc需小于0.1，该方法对数据扰动的概率λ才能处于其正确的区间[0,1]，更具体地，εc=0.01时，λ=0.82；而通常其他方法的εc取小数点后第1位即可.

给定参数n=106，εc=0.9，q=0.5，上述方法的对比结果如图7(a)所示.在该部分，本节实现了随机响应方法[51]和Laplace方法[46]作为本地化差分隐私(LDP)方法和中心化差分隐私(CDP)方法的实现与这些方法进行对比.结果显示，所有混洗差分隐私方法的RMSE都介于LDP与CDP方法之间，且计算代价和通信代价均高于这2种方法.不同混洗差分隐私方法中，Cnt_SGM有着最小的估计误差；而Cnt_2M由于使用了多消息模式编码，并为了保证计数为0时结果永远为0，对估计结果使用了较为暴力的截断，有着比其他方法明显较高的估计误差和通信代价，以及较低的计算代价.

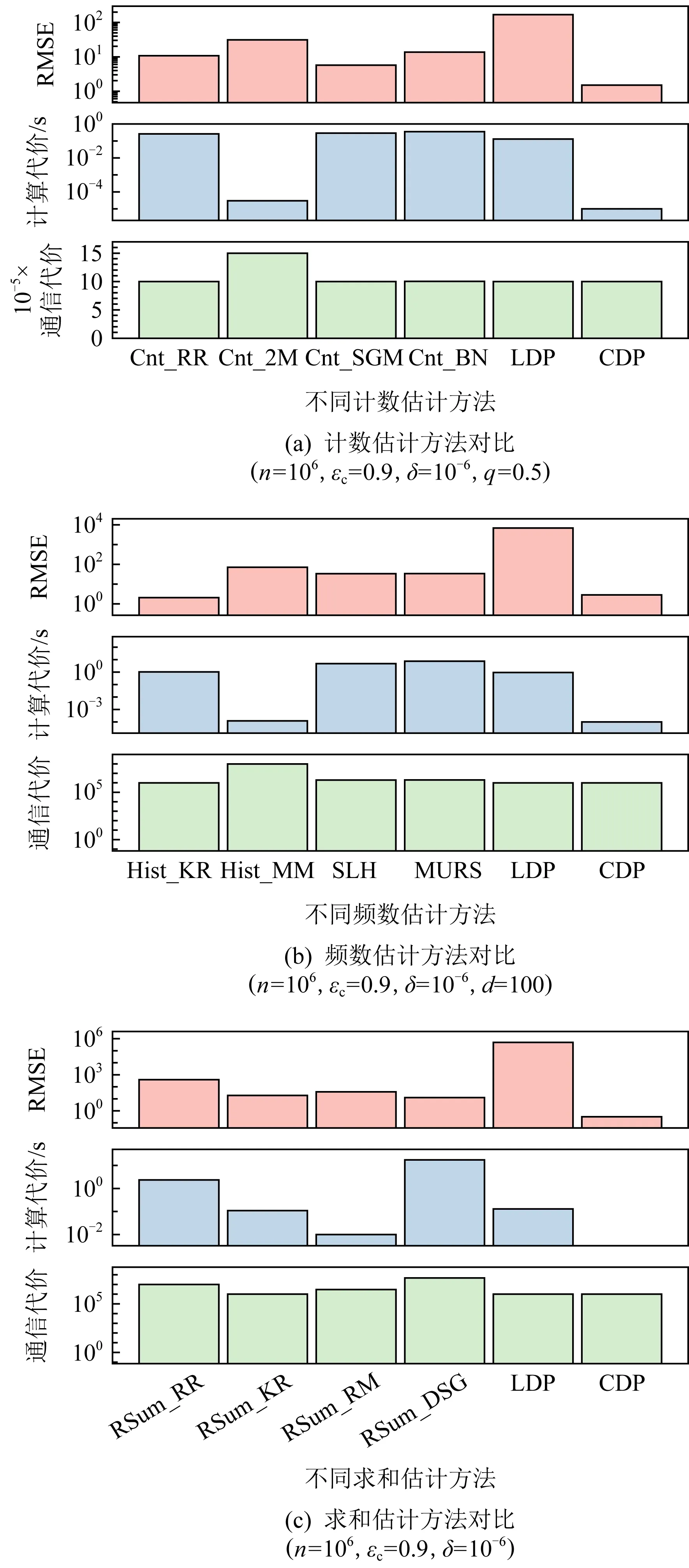
Fig. 7 Comparison of methods for different estimation issues

在图8～10中，分别评估不同εc，n和q对不同计数估计方法的影响.

1) 随着εc的增大，即隐私要求的降低，这些计数估计方法的误差都有明显减低，但计算代价和通信代价并无明显变化.

2) 随着n的增大，LDP方法误差增大，但混洗差分隐私方法的误差却几乎维持不动，进一步证明了在n较大的情况下混洗差分隐私方法的优越性.在计算代价和通信代价上，这些方法都随着n的增大而指数级上升.特别地，在对n值变化的实验对比中，Cnt_SGM方法一直维持着最小的估计误差；Cnt_2M方法不仅计算代价小，其计算代价增长的速度也比其他混洗差分隐私方法缓慢.

3) 随着q值的增加，数据集中1的数量变多，大多数混洗差分隐私方法的RMSE、计算代价和通信代价并无明显变化，Cnt_2M方法由于在用户端输出了更多扰动结果{1,1}，因此有着明显增加的通信代价.

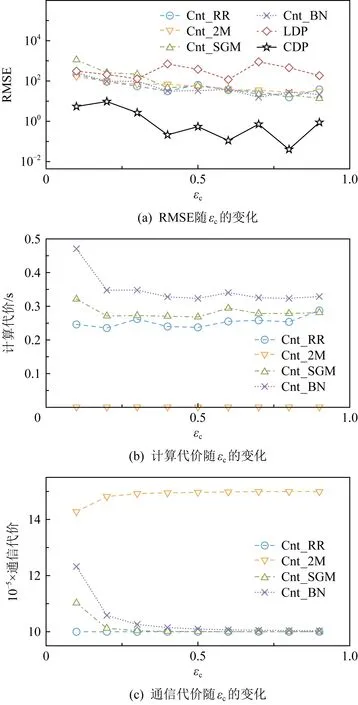
Fig. 8 Impact on counting estimation methods by varying εc

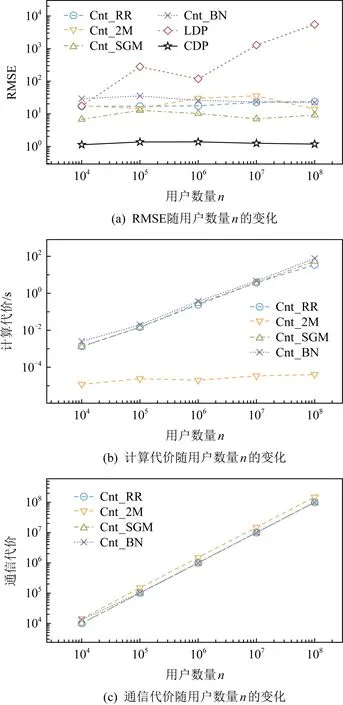
Fig. 9 Impact on counting estimation methods by varying n

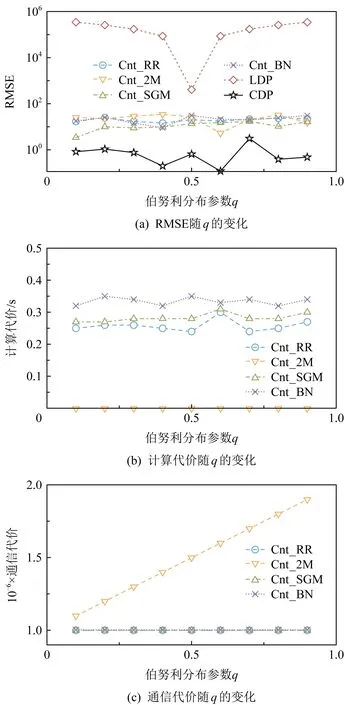
Fig. 10 Impact on counting estimation methods by varying q

5.2 频数估计实验评估

该节通过人工生成在给定值域[d]内满足正态分布的数据作为数据集，并假设每个用户拥有其中1个数值，对频数估计问题中的Hist_KR，Hist_MM，SLH，MURS进行评估，MURS方法实现时假设其添加假数据的数量为用户数量的1%.而PRHR由于计算代价和通信代价过大，不对其进行实验评估；PUCM适用于用户数量小于数据值域d的情况，亦难以与其他方法一同进行实验比较.具体地，在图7(b)所给定的参数下对PRHR方法进行评估，仅对30%用户数据进行编码就需要花费5 h并占用22 GB内存.对于同样计算代价较大的SLH和MURS方法，本节实现时通过预计算散列值与原值对应的索引表，并将该表保存，通过足够大的存储空间来换取实验结果中该方法较小的计算代价.由于现实世界中数据的存储相对廉价，该技巧对这2个方法的实际应用也是可行的.

图7(b)中对比的LDP方法是k值随机响应机制[27]，CDP方法是Laplace机制[46].在该图中，误差RMSE的纵轴坐标指数变化，Hist_KR方法有着最小的估计误差，与CDP方法近似.该结果产生的原因是，限于计算代价和通信代价，本实验选取了较小的值域对这些方法进行对比，而SLH，MURS方法主要针对值域较大的情况进行优化，当值域接近或大于用户数量时，这些方法才能体现出明显优势.从计算代价和通信代价上看，基于Cnt_2M方法实现的Hist_MM方法在这2方面均与其他方法有明显不同，并与Cnt_2M方法的实验结果相一致.

在图11～13中，分别评估不同εc，d和n对不同频数估计方法的影响.

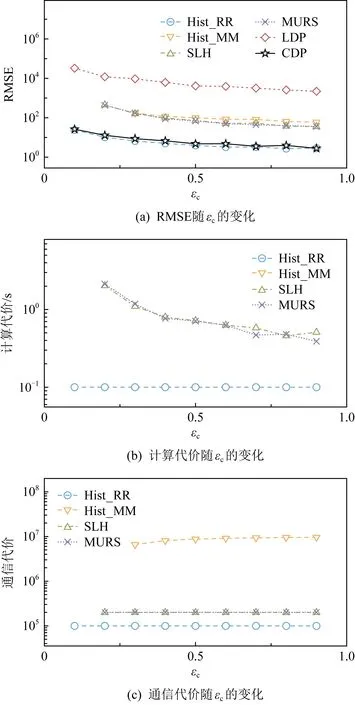
Fig. 11 Impact on frequency estimation methods by varying εc

1) 结果显示随着εc的增大，频数估计的误差和计算代价都有明显降低，通信代价几乎无变化，这与前面的理论分析是一致的.

2) 随着值域[d]的增大，Hist_KR方法的估计误差随之增大，与LDP方法变化的趋势一致；MURS方法的计算代价逐步增大，但其他混洗差分隐私方法并无明显变化，与4.2节的理论分析一致.

3) 随着用户数量n的增大，大多数方法在各个方面并没有显现出明显的变化，仅MURS方法的计算代价增加明显，这主要是混洗器添加假数据所造成的.而该实验设置中n仅从104变化到106，主要原因是除Hist_KR方法外，其他方法在本机模拟构建的总体计算代价过大(实验图仅展示分析器的计算代价)，难以进行评估.需说明的是，总体计算代价大并不代表实际中该方法难以应用，主要原因是实际应用时每个用户分别对自己的数据进行扰动，n个编码器是完全并行的；而本节进行实验模拟时这n个编码器串行或部分并行地计算，大多数消息模式方法的编码过程都长达数小时.

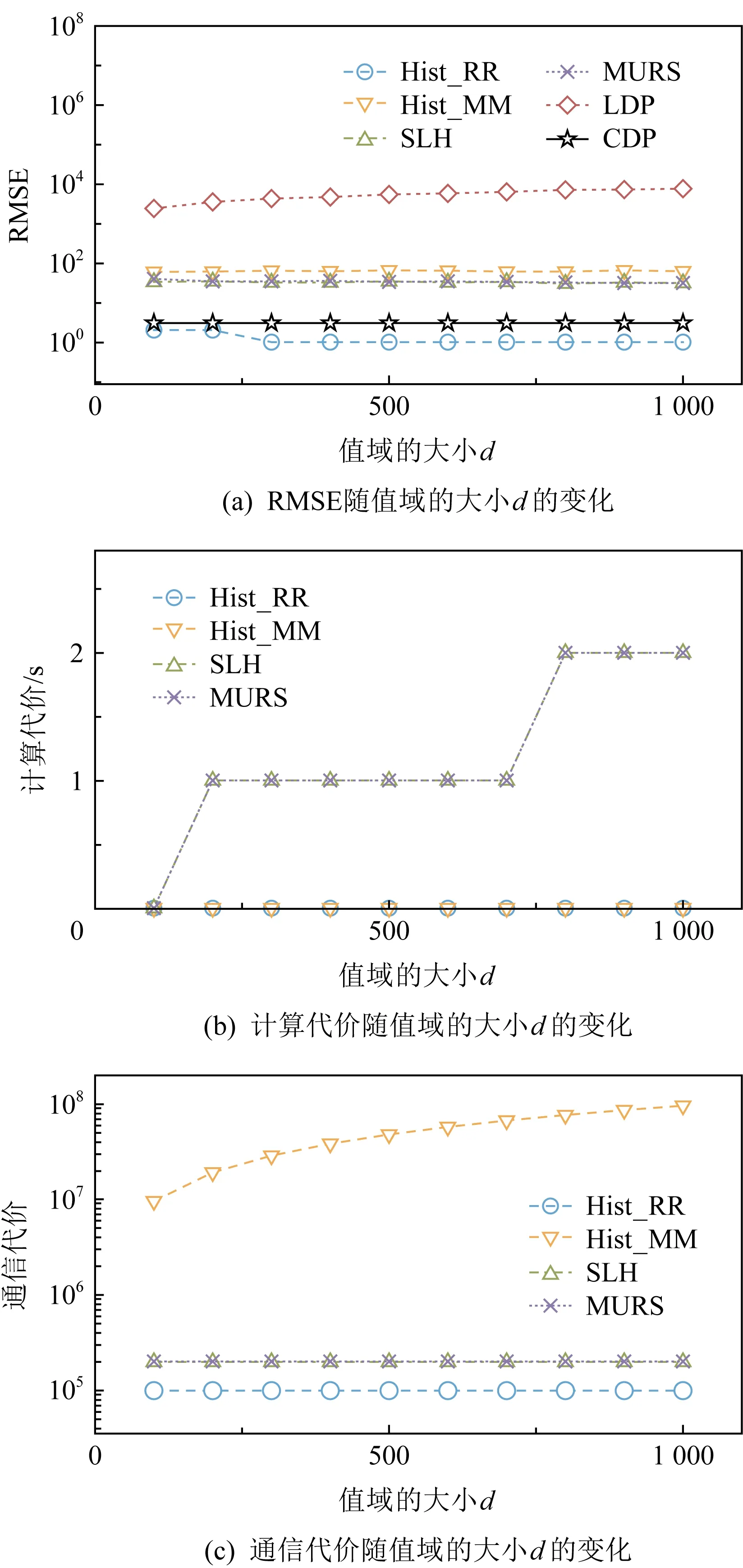
Fig. 12 Impact on frequency estimation methods by varying d

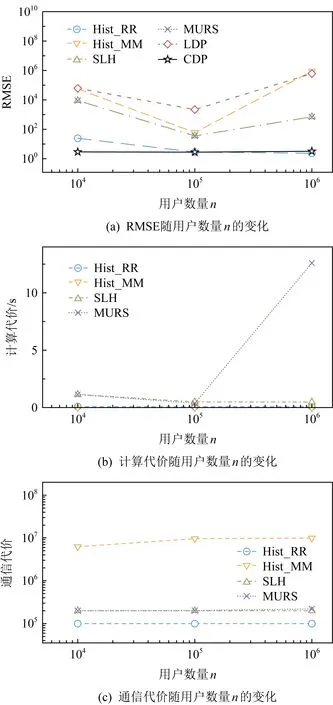
Fig. 13 Impact on frequency estimation methods by varying n

5.3 求和估计实验评估

该节通过人工生成满足正态分布的[0,1]数据作为数据集，并假设每个用户拥有其中1个数值，对求和估计问题中的RSum_RR，RSum_KR，RSum_RM，RSum_DSG进行评估.由于RSum_PURE方法基于Cnt_PURE方法实现，基于5.1节的分析，不对其进行实验评估.

图7(c)中，用作对比的LDP方法是Harmony机制[70]，CDP方法是Laplace机制[46].该实验中，将RSum_RM方法中多消息模式的消息数量设为3，其他方法随机舍入的精度设为10.结果显示，RSum_RM方法有着接近小的估计误差和明显较小的计算代价，RSum_DSG虽计算代价和通信代价较大，但估计误差在所有混洗差分隐私方法中最低，与4.3节的理论分析一致.

在图14，15中，分别评估不同εc和n对不同求和估计方法的影响.

1) 结果显示，随着εc的增大，求和估计的误差有明显降低，但计算代价和通信代价并无明显变化.

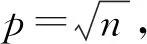
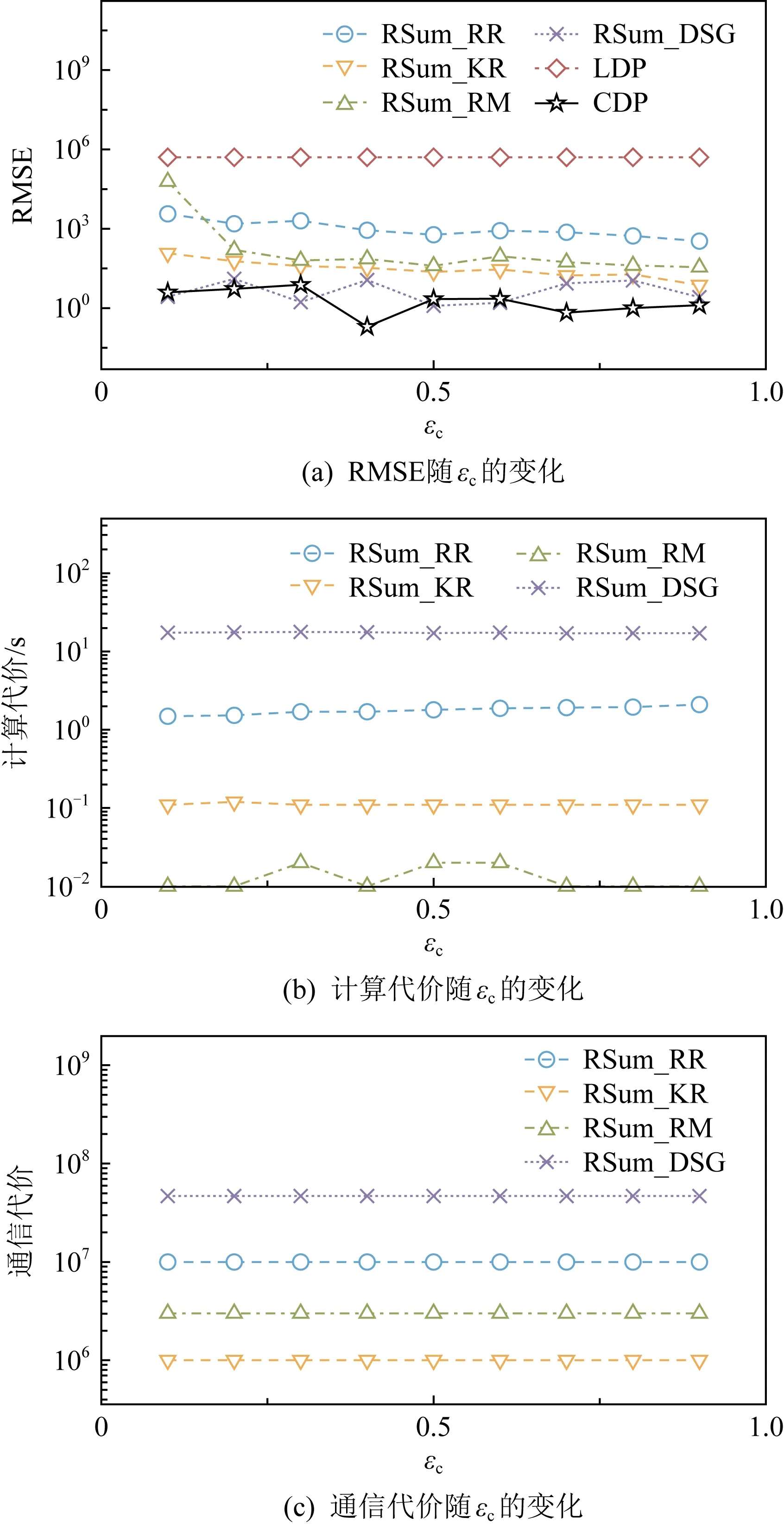
Fig. 14 Impact on sum estimation methods by varying εc

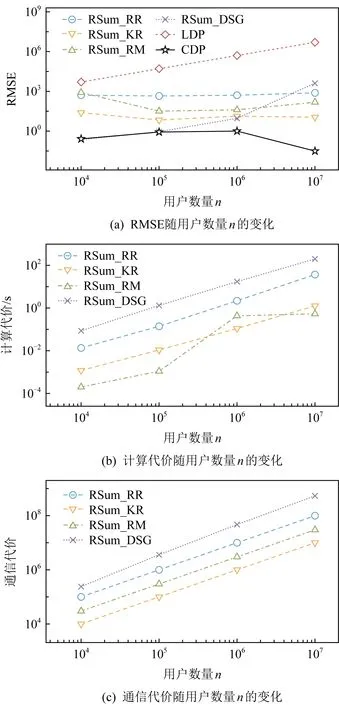
Fig. 15 Impact on sum estimation methods by varying n

5.4 实验小结

从实验分析的总体上看，混洗差分隐私方法在各统计问题的结果可用性上都有着相比本地化差分隐私方法明显更优的结果.但从通信代价和计算代价的角度分析，ESA框架中混洗器的引入，一方面使得用户数据与用户所使用的编码器之间的关联性消失，使得分析器端的计算代价增大；另一方面促使研究者们使用富含信息更多的多消息模式对数据编码，造成了分析器端的通信代价增大.如何兼顾数据的隐私性、可用性、方法的计算代价和通信代价是后续基于ESA框架构建的隐私保护方法需加以考量的部分.

从各混洗差分隐私方法评估的结果看，随着εc的增大，各方法的数据可用性均会得到提高；而随着用户数据n的增加，基于本地化差分隐私方法设计的混洗差分隐私方法在计算误差上会有轻微的增加，其他大多数混洗差分隐私方法在计算误差上没有明显变化，甚至部分方法有着轻微的降低.总体上，基于多消息模式设计的混洗差分隐私协议由于携带了更多与用户数据相关的信息，有着相对较高的数据可用性，与第4节的理论分析相一致.

6 挑战问题

当前对ESA框架的研究，以混洗差分隐私方法为主，而该方法主要聚焦于理想假设下的理论研究，重点侧重在2个方面：一方面是对该机制本身的隐私放大等理论的研究；另一方面致力于统计问题的估计，以谋求比LDP方法更高的可用性，比CDP方法更好的隐私性.但ESA框架在实际应用上，仍存在着诸多挑战，这些挑战问题一部分是ESA框架与生俱来的，另一部分是差分隐私方法的应用所带来的.由此，本节提出，在ESA框架下探索非差分隐私的隐私保护方法以应对更多更为复杂的隐私问题，是ESA框架未来发展的主要挑战与趋势.

6.1 ESA的有效性

如实验部分所示，ESA框架中混洗器的引入，打破数据之间的关联性，有效增加了数据的隐私性和可用性，但相比同类方法，分析器端存在着明显增加的计算代价和通信代价.同时由于混洗器本身通常基于MixNet等密码学网络构建，对加密数据的安全混洗操作本身就有着昂贵的计算与通信开销.带宽受限、算力受限、需要处理实时任务，这些都是ESA框架应用受阻的重要因素.如何基于该框架设计兼顾隐私度、准确度、计算代价和通信代价的隐私保护方法是ESA框架的挑战之一.

对于基于ESA框架实现的混洗差分隐私，为提高结果的准确性，设计方法通常会引入如散列簇、多消息模式的编码器、多混洗模式的混洗器等方法对数据进行处理，往往伴随着计算代价或通信代价的增加.尽管保证数据隐私性和可用性是差分隐私方法的核心，算法的计算代价和通信代价亦不容忽视.

6.2 ESA的鲁棒性

ESA框架中的混洗器作为ESA框架隐私保护的核心组件，存在着单点失败的可能，极易对整个框架的平稳运行造成影响.一旦框架中的混洗器出现问题，如被攻击、与分析器合谋、宕机等，分析器便不能收集或收集到错误的用户信息.如何增强混洗器在实际应用过程中的鲁棒性，对其混洗结果的正确性进行有效验证，亦是ESA框架的挑战之一.

对于基于ESA框架实现的混洗差分隐私方法，其方法的鲁棒性难以得到保证.一方面，当前方法假设参与计算的n个用户是可信用户，且会几乎同时发送他们扰动后的数据给混洗器.但实际问题中，该条件很难获得保证.基于现有的上述方案，当存在用户端被攻击者控制或网络状况差使用户掉线时，要么混洗器需等待极其长的时间，收集满足要求(有时是为了满足隐私放大定理中的参数n)的足量数据；要么，分析器会得到可用性和隐私性都相对理论较差的结果.另一方面，当前的混洗器分为单混洗器模式和多混洗器模式2种，但无论哪种，任一混洗器失效都会使系统存在单点失败的可能.应用现有的具有鲁棒性的秘密共享机制实现混洗器[32]是一种可能的解决方案，但应如何与基于ESA模型实现的具体问题进行结合，尚待研究.

此处，仍需重复阐明一点，第4节中介绍的部分方法可实现具有鲁棒性的差分隐私RSDP，但该鲁棒性并非本节所探讨的系统鲁棒性.RSDP的鲁棒性是仅针对隐私而言，即保证可信用户数量大于一定阈值γ时，分析器端依旧可以获得满足(ε,δ)-DP，该定义不对与数据的可用性、算法(尤其是混洗器)的等待时间、混洗器本身相关的鲁棒性做任何定义与约束.

6.3 ESA的复杂问题应用

当前ESA框架主要通过与差分隐私结合，用于解决简单的统计问题，但ESA框架本身应支持解决更复杂的问题，并不局限于此.具体而言，该复杂问题应包含2类：

一类是ESA与差分隐私结合可能解决，但尚未解决的复杂问题.如值域未知情形下的混洗差分隐私、高维度数据上的混洗差分隐私、复杂数据类型上的混洗差分隐私等.在实际应用中，这样复杂的应用场景随处可见，如当需要对用户浏览的网页进行统计时，由于网页的数量在不断增长，很难对当前作为候选集的网页进行枚举，需可处理值域未知的混洗差分隐私方法；又如，将混洗差分隐私应用在机器学习上，往往涉及到成千上万个维度的数据，需有效的隐私保护方法对其进行处理；再如，生活中常见的相对复杂的键值对类型数据，如果对键与值分别扰动，键与值之间的关联性很可能被混洗器打断，难以获得有效的估计结果.这些问题通过应用散列函数映射[52]、数据降维[71]等可能会被解决，但如何应用仍是挑战.

另一类是ESA可能解决，但差分隐私不能解决的问题，需要基于该框架对非差分隐私的方法进行探索.具体而言，差分隐私本质上可用于回答“有多少”的问题，而不是回答“是什么”的问题，对一个点是不是异常点、一个人是不是新冠肺炎的感染者这样的问题，应用差分隐私将这些数据进行扰动并不能得到可用的答案，差分隐私更趋向于将这样出现频数极低的点抹平，使其不在结果中凸显以保护隐私[72-73].但ESA框架为这样问题的回答创造了可能性，即ESA框架可在对数据进行尽可能少的扰动情况下保护隐私，便为异常点检测、新冠肺炎发现这样的问题提供条件.由此，发展非差分隐私的ESA方法十分关键!

6.4 ESA与联邦学习

联邦学习算法近2年在工业界和学术界迅速发展，该模型一定程度上打破数据孤岛，解决了隐私问题[74].该模型的基本思想是基于用户或企业独立的数据在本地进行模型的训练与更新，将模型的参数(如梯度)在服务器端进行安全聚合，从而训练一个中心化的模型提供服务器.虽然联邦学习不直接传递用户数据，仅与服务器共享模型参数，但该参数往往包含着一定程度的用户隐私，易遭受成员推理攻击[75-76]，需使用高可用性的隐私保护方法进行保护.

ESA框架与联邦学习均适用于用户在本地端进行数据处理，对处理后数据进行收集的场景，ESA框架本身的特性与联邦学习的需求不谋而合.ESA与联邦学习最简单的结合，即使用第4节所述的混洗差分隐私方法对用户共享的梯度进行保护，但该方法如何适用于参数维度巨大的机器学习模型的训练仍是难点[77-78].同时，混洗差分隐私虽相比本地化差分隐私方法引入了较小噪声，但在数据量较小、隐私损失较小的情况下仍对数据可用性有着不小的威胁.基于ESA框架发展与联邦学习高度适配的隐私保护方法应该是该方向的主要挑战.

7 结束语

数据驱动的人工智能时代，数据隐私问题备受关注，但数据可用性亦是社会与科技发展的重中之重.ESA框架为提出数据可用性更好、隐私性亦更好的隐私保护方法开辟了新的路径，混洗差分隐私即为该框架下的典型方法.混洗差分隐私方法兼具了本地化差分隐私在数据收集场景中的易用性和中心化差分隐私在数据分析结果上的可用性，在多种统计问题上的表现卓越.本文对ESA框架及其应用——混洗差分隐私方法进行了详细的综述，对混洗差分隐私下的研究方向进行总结，针对不同统计问题的若干算法进行理论分析与实验对比.基于上述总结分析的结果，本文提出了当前ESA框架应用面临的主要挑战，并以混洗差分隐私为例对这些挑战进行详细的说明.本文提出，混洗差分隐私是ESA框架应用的有效途径，但不是唯一途径，存在着诸多具有现实意义的复杂问题混洗差分隐私难以解决，但ESA为这些问题的解决创造了条件.基于ESA框架探索适用性更广的、可用性更高的、非差分隐私的隐私保护算法是数据隐私保护未来可能的发展方向之一.

作者贡献声明：王雷霞负责论文总结、撰写与实验；孟小峰指导总体架构.