基于二元Logit回归模型的大学生学业问题影响因素研究*
2022-01-19王红青赵祖平
王红青,陈 波,赵祖平,宋 菁
(三峡大学科技学院,湖北 宜昌443002)
随着高等教育规模不断扩大,生源质量和类型发生变化,学生人数剧增,生源质量参差不齐,学生情况多样化,就业压力增大间接带来的学业压力增大等,导致不少学生缺乏自控能力并出现学业问题,无法顺利完成学业。
本文通过调查问卷的方式,研究学业问题的影响因素,提出有针对性的应对方案,为学业出现问题的学生合理安排学习进程,提供必要的帮扶措施,帮助其更好地完成学业,最终实现高等教育的根本目的,以期为高校学业预警机制建设方面提供参考途径。
1 调查方案与数据分析
1.1 调查方案
根据研究需要设计了调查问卷,内容包括基本信息、学业成绩认知、学业现状及问题、学业预警制度认知、学业预警实施现状及评价5个维度,共40道题目。研究团队在S高校面向本科生开展了问卷调查,采取自愿原则、实名制方式,保证了调查数据的科学性与准确性。调查共回收1 486份问卷,剔除无效问卷后,有效问卷数量1 476份,有效问卷率为99.33%。被调查样本中,男生占39.43%,女生占60.57%。调查问卷选项“是否出现过学业问题”中,出现过学业问题的样本数量为520人,占调查总人数的35.23%,符合分析要求。使用SPSS软件对样本的定量问题进行信度分析,得出克隆巴赫α系数信度系数为0.869,说明研究数据信度质量良好,可用于进一步的研究分析。
1.2 统计分析
总共有1 476个样本参加分析,且没有缺失数据。对自变量项进行描述性统计及交叉分析。对大学生是否出现过学业问题的因素进行统计。具体统计结果如表1所示。
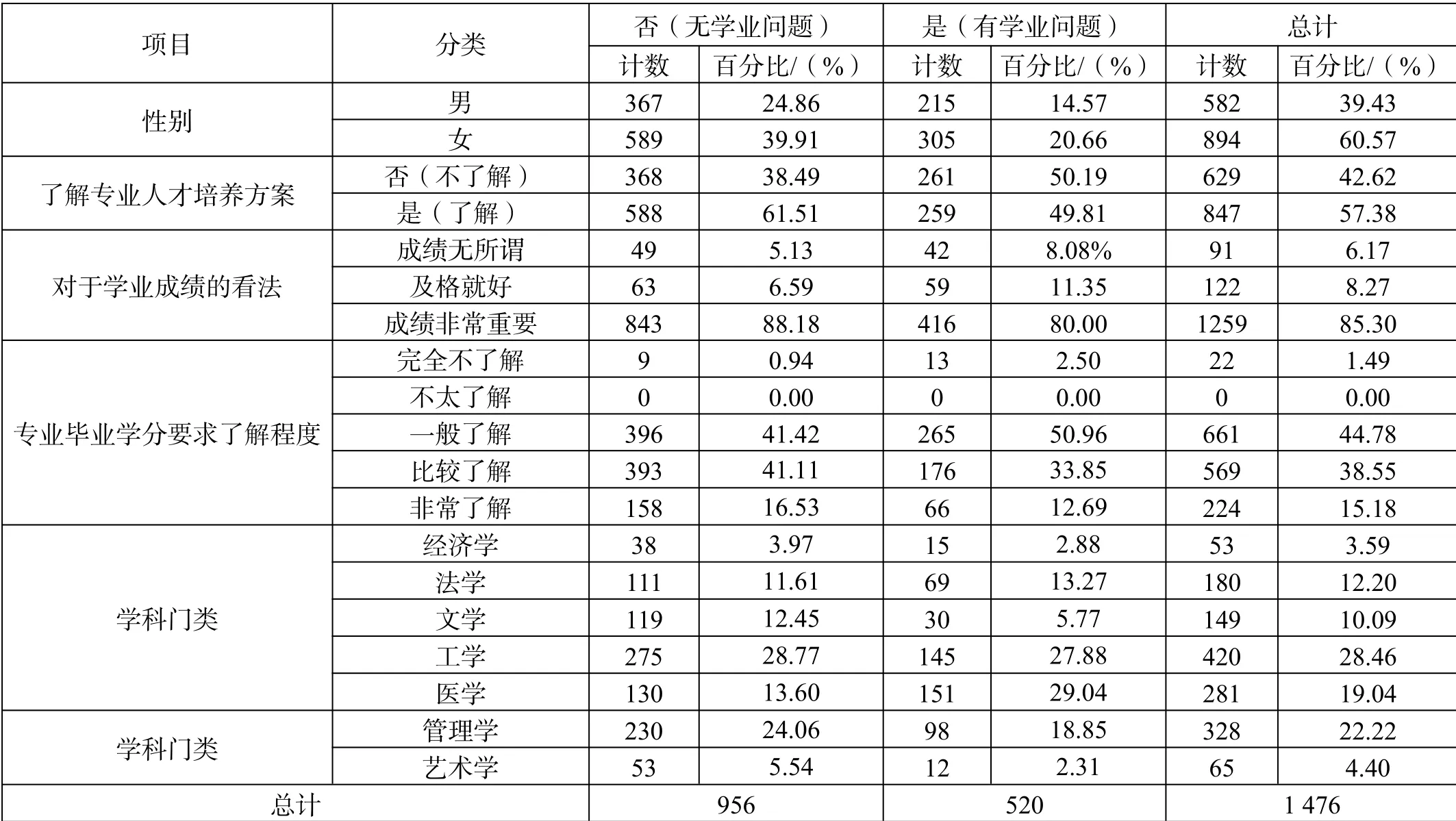
表1 大学生是否出现过学业问题的因素统计表
采用卡方检验方法研究不同性别样本对于是否出现学业问题的差异关系,男女生在出现学业问题上,前者占14.57%,后者占20.66%,结果显示无显著性差异。有无学业问题两类学生样本对于是否了解专业人才培养方案呈现出0.01水平显著性(Pearson χ2=18.849,P=0.000<0.01),通过对比差异可知,有学业问题的学生“不了解培养方案”的比例为50.19%,明显高于无学业问题的学生比例(38.49%)。无学业问题学生“了解培养方案”的比例为61.51%,明显高于有学业问题的学生比例(49.81%)。对于学科门类呈现出0.01水平显著性(Pearsonχ2=71.150,P=0.000<0.01),通过对比差异可知,两类学生样本对于不同的学科门类呈现出0.01水平显著性,医学学科有学业问题的学生比例为29.04%,明显高于无学业问题学生比例(13.60%);文学学科有学业问题的学生比例为5.77%,明显少于无学业问题学生比例(12.45%);管理学学科有学业问题的学生比例为18.85%,明显少于无学业问题学生比例(24.06%)。
利用方差分析法研究样本中有、无学业问题两类学生对于“是否了解本专业的毕业学分要求、如何看待成绩好对提升自身能力有帮助、如何看待成绩好对毕业以后的发展有帮助、了解学校关于学业预警的相关规定、学业预警制度能提高你学习的自主性、学业预警对自己的行为是否具备足够的约束力”共6项定量题项的差异性。结果显示,两类学生样本对上述6项全部均呈现出显著性(P<0.05),均呈现出显著性差异。
结果表明,与不存在学业问题的学生相比,存在学业问题的学生不太了解专业毕业学分要求,也不太了解学校学业预警相关规定。不存在学业问题的学生更倾向于认可成绩好对提升自身能力有帮助、对毕业以后的发展有帮助的观点,他们认为学业预警制度可以提高学习的自主性,具备足够的约束力。方差分析结果如表2所示。
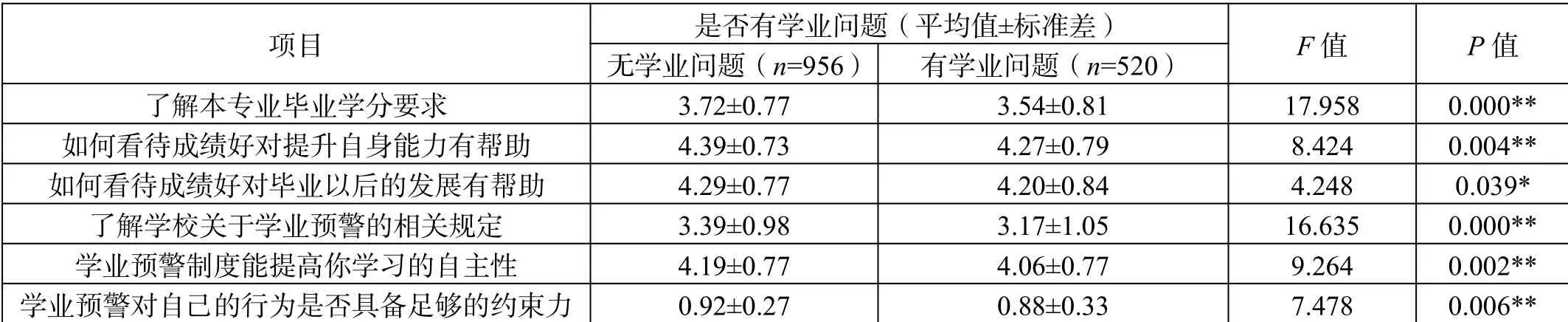
表2 方差分析结果
2 模型构建与实证分析
2.1 模型的构建
本文的研究目的是探讨学业问题的影响因素,“是否出现学业问题”为定类数据且值为两项,是或否,因而适用于二元Logit回归分析方法。二元Logit模型的被解释变量是二分类变量,模型常用于研究分类概率与解释变量之间的关系。
通过分析,产生学业问题的因素主要有“是否了解专业人才培养方案”“学科门类”“对于学业成绩的看法”“本专业毕业学分要求了解程度”4个潜在的自变量影响因素,被影响项为因变量“是否出现过学业问题”。
构建二元Logit模型可分为3步:确认危机事件,构建模型的因变量,将因变量与自变量代入模型并得出最终结果[1]。
构建模型:

式(1)中:P为发生学业问题的概率;1-P为不会发生学业问题的概率为模型的截距项;为解释变量(自变量);
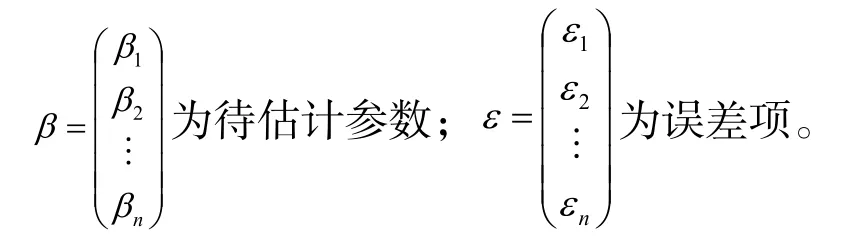
对模型整体有效性进行分析。二元Logit回归模型似然比检验结果如表3所示,从表3中可知,模型检验的原定假设为:是否放入自变量两种情况时模型质量均一样。结果表明,P值小于0.05,因此拒绝原定假设。即说明本次构建模型时,放入的自变量具有有效性,本次模型构建有意义。

表3 二元Logit回归模型似然比检验结果
2.2 结果分析
本次调研采用SPSS 26.0软件、SPSSAU[2]网页版数据科学算法平台工具及WPSOffice软件对问卷结果进行综合统计分析,各变量回归分析结果如表4所示。
最终的模型表达式为:ln(P/1-P)=0.020-0.365×是否了解专业人才培养方案(是)+0.748×学科门类(管理学)+1.812×学科门类(医学)+0.936×学科门类(工学)+0.182×学科门类(文学)+1.118×学科门类(法学)+0.791×学科门类(经济学)-0.614×对于学业成绩的看法(成绩非常重要)-0.248×专业毕业学分要求了解程度。
由表4可知,学科门类医学、法学、工学、管理学会对学生在“出现学业问题”上产生显著的正向影响关系,学生了解专业人才培养方案、认为学业成绩非常重要、本专业毕业学分要求了解程度3个指标项会对学生在“出现学业问题”上产生显著的负向影响关系,具体如下:①学生对人才培养的了解每增加一个单位时,学生在“是否会出现学业问题”的变化(减少)幅度为0.694倍。②学业成绩的看法是(非常重要)每增加一个单位时,学生在“是否会出现学业问题”的变化(减少)幅度为0.541倍。③学生对毕业学分要求的了解程度每增加一个单位时,学生在“是否会出现学业问题”的变化(减少)幅度为0.781倍。④学科门类以艺术学作为对比项,与艺术学类学生样本相比,结果发现,医学、法学、工学、管理学类学生出现学业问题比例要远远高于艺术学类学生,分别为艺术类学生的6.122、3.059、2.550、2.112倍。经济学、文学回归系数值为0.791、0.182,未呈现出显著性。
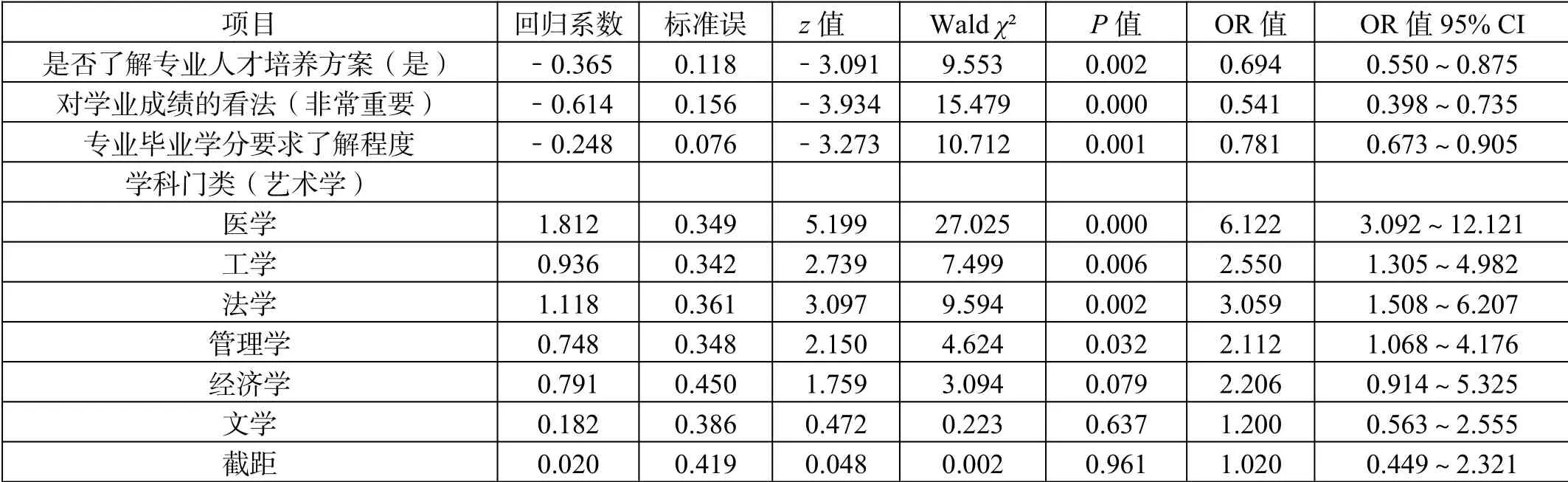
表4 二元Logit回归分析结果汇总
通过模型预测准确率去判断模型拟合质量,模型的整体预测准确率为67.21%,模型拟合情况不太理想。但本研究模型重点在于找出对学业问题有影响的因素,因此准确率的关注意义较小。使用Hosmer-Lemeshow拟合度检验用于分析模型拟合优度情况,P值大于0.05(Pearsonχ2=5.327,P=0.722>0.05),即说明研究模型通过HL检验,拟合优度较好。
3 研究结论与建议
研究结果表明,S高校医学、法学、工学、管理学学科学生出现学业问题的可能性更高;学生了解人才培养方案,认为成绩非常重要,对毕业学分要求了解程度越高,越不容易出现学业问题。根据以上研究结论,本文建议事前提出预警,有效避免学业问题,事中、事后提供必要的帮扶措施,帮助学生更好地完成学业,具体如下:①建立科学的学业预警制度。建立和完善学校学业预警机制,建立科学的学业预警制度的途径。制定配套的学业预警工作管理办法,建立一套科学的学业预警体系。加强学业预警管理的队伍建设,建立完善上下贯通、执行有力的组织体系,建立一支专业化的管理队伍。构建预警信息管理平台,推进学业预警管理信息化建设,运用现代信息技术手段,为学业预警工作机制顺利运行提供强有力的保障。②建立多层次学业帮扶体系。做好新生入学教育工作;加强学业指导工作,在学校现有“新生导师制”的基础上,组建一支专业的学业指导队伍,统筹推进全校学业指导工作。加强心理健康教育工作,构建和完善大学生心理问题预警和干预机制。③建立多元主体协作平台。进一步落实学校、学生、家长三方互动育人机制,充分发挥学校、家庭合力教育的功能,由学校主导,积极引导学生自主参与、家庭主动参与到学业预警工作中,共同做好学业帮扶工作。
