基于Copula密度函数的毛竹胸径年龄结构特征二元联合分布*

刘恩斌 姚鸿文 任泽茜 周国模 杜华强

(1.浙江农林大学省部共建亚热带森林培育国家重点实验室 浙江省森林生态系统碳循环与固碳减排重点实验室 浙江农林大学环境与资源学院 杭州 311300;2.伦敦大学学院地理系 伦敦 WC1E 6BT；3.浙江省森林资源监测中心 杭州 310020)

毛竹(Phyllostachysedulis)是我国南方重要的森林资源之一，生长快、成材早、产量高、伐期短、收益期长,不仅具有较高的经济价值和社会价值，而且其光合能力较强，全年都能维持良好的生物量和碳储量，具有重要的生态功能(周国模等，2004；方晰等，2002；李意德等，1998；阮宏华等，1997)。毛竹生长过程中，主要依靠地下茎(俗称竹鞭)上的笋芽逐步发育成竹笋，再长成新竹，新竹在第一年内即可完成胸径、高度生长，之后虽然胸径和竹高不再发生改变，但生物量会随年龄增长而变化，因此，胸径和年龄是影响毛竹林生物量易测易辨的独立变量。

毛竹林胸径与年龄联合分布较一元分布更能完整反映其资源结构特征，精确预估各径阶、各龄阶株数以及产量、枯损量等，为毛竹林经营决策提供科学依据；且结合毛竹胸径年龄二元单竹生物量模型(周国模，2006)，还能对区域尺度毛竹林生物量进行精确估算，为毛竹林碳库精准测算奠定基础。到目前为止，二元广义β、二元Johnson’s Sbb、二元Weibull等分布函数常被用来描述森林结构特征因子的二元分布，如采用二元广义β和 Johnson’s Sbb分布函数描述胸径树高二元联合分布(Lietal.，2002；Gorgosovarelaetal.，2019；Cardil Forradellasetal.，2016；Wangetal.，2007；Mnness，2015)基于二元Weibull和二元β分布函数描述树冠内细枝叶面积分布的二维结构以及毛竹胸径年龄联合分布(Temesgenetal.，2003；葛宏立等，2008；刘恩斌等，2010)等，森林结构特征因子的概率分布对森林生物量估算及森林经营具有非常重要的作用。但已有森林结构特征因子二元联合分布研究方法存在如下缺陷：1)2个森林结构特征因子的边缘分布函数类型必须相同，如二元β、二元Weibull和二元Sbb的边缘分布函数必须是一元β、一元Weibull和一元Sbb分布函数，在实际应用过程中，当2个森林结构特征因子的边缘分布函数类型不同时，常用二元分布函数不能描述2个因子的联合分布，适用性不广；2)不能由边缘分布确定对应的联合分布，森林结构特征因子二元联合分布研究通常先建立联合分布函数，后推导联合分布对应的边缘分布(葛宏立等，2008；刘恩斌等，2010；Hafleyetal.，1976)，建立的联合分布函数不是由对应的边缘分布函数确定的，事实上，边缘分布函数的类型和理论较联合分布函数更多、更完善，但理论和应用价值远不及联合分布函数，根据森林结构特征因子的边缘分布函数建立其对应的二元联合分布函数具有重要意义；3)拟合参数需要森林结构特征因子联合分布(密度)的实测值，这在很多情况下难以满足，如要研究2014年浙江省毛竹胸径年龄的二元分布结构，从已有数据资料能够获得每块样地各径阶、各龄级的毛竹分别有多少株，但无法获得每块样地中每株毛竹的胸径和年龄实测数据，即只能得到全省毛竹胸径和年龄的边缘分布值，无法获得全省毛竹胸径和年龄的联合分布值；再如要研究某区域杉木(Cunninghamialanceolata)胸径树高二元联合分布，从各种文献中获取满足该区域抽样精度的2套样本，一套可得到胸径分布值，另一套可得到树高分布值，但由这2套样本无法得到杉木胸径树高联合分布值，也就无法使用常用二元分布函数构建其对应的联合分布模型。

随着科学研究的逐步推进，在统计领域快速发展的Copula函数理论为解决上述相关非正态变量建模问题提供了新思路(Nelsen，1998)。Copula函数理论的核心思想是任意一个二元联合分布函数均可拆分为1个包含相关性大小和相关结构信息的Copula分布(密度)函数与2个对应的边缘分布函数，其在建模时的灵活性和适应性具有无可比拟的优势，如2个森林结构特征因子的边缘分布函数类型可以不同、可由边缘分布函数确定其对应的联合分布(密度)函数、对实测值依赖性不强等，已在金融和水文等领域广泛应用(张尧庭，2002；谢华等，2012；Sklar，1959；Fangetal.，2020；Wangetal.，2016)。在林业领域也有相关研究，如采用三元Copula函数对单株材积进行估算(Petrauskasetal.，2011；Wangetal.，2010)，采用二元Copula函数描述树木胸径树高联合分布与树高曲线(Wangetal.，2008；Oganaetal.，2020；Gorgoso-Varelaetal.，2016；Rupšysetal.，2012)，还用于河岸林下植被盖度的估算(Eskelsonetal.，2011)以及林分结构特征因子的模拟(Kershawetal.，2010)等，但用于描述毛竹林分结构特征因子联合分布的研究鲜见报道。鉴于此，本研究针对森林结构特征因子常用二元联合分布研究方法存在的缺陷，选择适用条件低、适应范围广、应用价值大的二元Copula密度(分布)函数构建毛竹胸径年龄二元联合分布模型，以期为精确测量森林结构特征因子联合分布提供参考。

1 材料与方法

1.1 试验材料

浙江省于1979年建立森林资源连续清查体系，以5年为一个复查周期，固定样地4 250块，样点格网大小为4 km×6 km，样地形状为正方形，边长28.28 m，面积800 m2。本研究利用2009年浙江省177块毛竹连续清查固定样地数据进行描述。样地调查因子包括土层厚度、海拔、坡位、坡度、坡向、样地毛竹平均胸径、样地毛竹株数以及样地内每株毛竹的胸径和年龄等。经统计，各样地毛竹株数22～897不等，胸径5～15 cm，年龄1～5度(当年生毛竹记为1度竹，2～3年生毛竹记为2度竹，依此类推)，具体数据见表1。

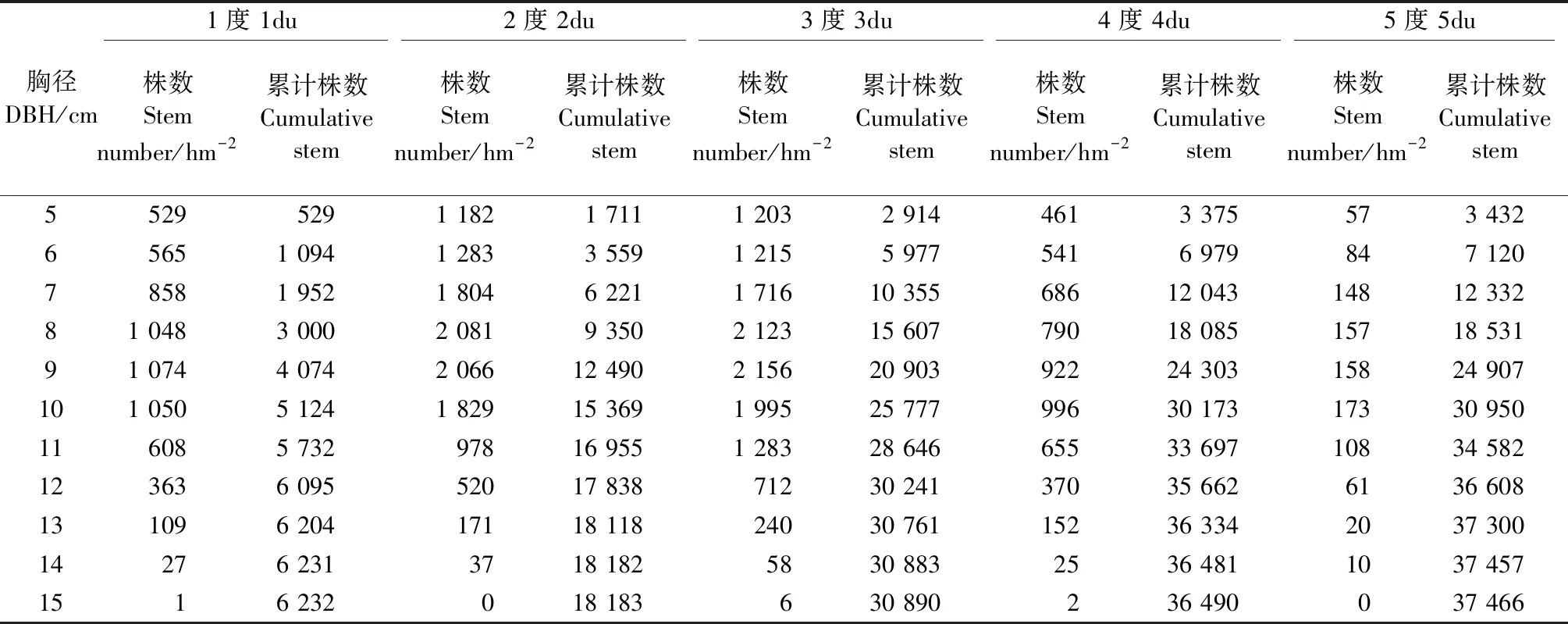
表1 浙江省毛竹林胸径、年龄统计数据Tab.1 Statistical data of DBH and age of moso bamboo forest in Zhejiang Province

1.2 研究方法

1.2.1 基本公式 借用Coupla函数理论，设D为胸径、A为年龄，令u=F(D)和v=G(A)分别为毛竹胸径和年龄的边缘分布函数，则对于毛竹胸径年龄联合分布函数H(D,A)，存在着一个Copula分布函数C，使得

H(D,A)=C[F(D),G(A)]。

(1)

设毛竹胸径年龄的二元Copula分布函数和密度函数分别为C(u,v)和D(u,v)，则由式(1)得：

(2)

令f(D)=∂u/∂D为胸径D的边缘概率密度函数，g(A)=∂v/∂A为年龄A的边缘概率密度函数，则毛竹胸径年龄的联合概率密度函数h(D,A)为：

(3)

有关Copula密度函数更详细的介绍参考有关文献(Sklar，1959；Fangetal.，2020；Wangetal.，2016)。具体应用时，可根据毛竹连续清查数据确定其胸径和年龄的边缘分布函数值。

常用Copula密度函数包括正态Copula、t-Copula和阿基米德Copula密度函数，其中Gumbel Copula、Clayton Copula和Frank Copula密度函数是最常用的3种阿基米德Copula密度函数(张蕾，2017)。

1.2.2 最优Copula密度函数识别方法 二元正态Copula和二元Frank Copula密度函数适合描述具有对称尾部且尾部渐进独立的二维森林结构特征因子，二元t-Copula密度函数适合描述具有对称尾部且尾部相关的二维森林结构特征因子，二元Gumbel Copula密度函数适合描述具有非对称尾部且上尾相关、下尾渐进独立的二维森林结构特征因子，二元Clayton Copula密度函数适合描述具有非对称尾部且下尾相关、上尾渐进独立的二维森林结构特征因子。

赤池信息准则(Akaike information criterion，AIC)是衡量统计模型拟合优良性(goodness of fit)的一种标准，其以极大似然函数为基础评价概率密度模型拟合数据的优良性。本研究采用AIC识别最优Copula密度函数，计算公式为：

(4)

式中：m为所选模型参数个数；L为所选分布的极大似然函数；N为拟合的原始数据样本量；当所选模型为二元 Gaussian Copula、二元Frank Copula、二元Gumbel Copula和二元tClayton Copula密度函数时，m=1；当所选模型为二元-Copula密度函数时，m=2；ui,vi(i=1,2,…,N)为原始样本数据第i个胸径和年龄的边缘分布函数值；θ为所选模型参数；D(ui,vi;θ)为所选模型的概率密度函数值。

对比所有备选密度函数的AIC，AIC越小，表明密度函数拟合原始数据的性能越好。

1.2.3 毛竹胸径年龄二元Copula密度模型 为更好说明二元Copula密度函数的性能，利用2009年浙江省177块毛竹连续清查固定样地数据，采用Matlab软件编写极大似然算法，应用上述5个二元Copula密度函数对毛竹胸径年龄的联合密度函数进行研究，并根据AIC从5个二元Copula密度函数中优选出1个最优二元Copula函数，进而构建浙江省毛竹胸径年龄二元Copula密度模型。

1.2.4 最优Copula密度函数与常用二元分布函数的对比分析 从测量精度、参数个数和参数迭代收敛性3方面，对毛竹胸径年龄最优Copula密度函数、二元Weibull分布函数和二元Johnson’s Sbb密度函数进行深入分析。由于二元广义β概率密度函数参数较多，采用已有参数估算方法(Lietal.,2002)多次尝试后迭代始终不收敛,故本研究未选用。

采用Matlab软件编写程序并进行绘图。

2 结果与分析

2.1 最优二元Copula密度函数的选取

2.1.1 毛竹胸径年龄累计分布二维频数直方图 根据表1得出毛竹胸径和年龄的累计分布值，绘制毛竹胸径年龄累计分布的二维频数直方图(图1)。令u、v分别为胸径(D)和年龄(A)的累计分布函数值，则图1即(u,v)联合频数直方图，可作为(u,v)二元Copula密度函数图像的形状。可以看出，毛竹胸径年龄密度函数具有不对称尾部，上尾相关性大、下尾渐进独立。

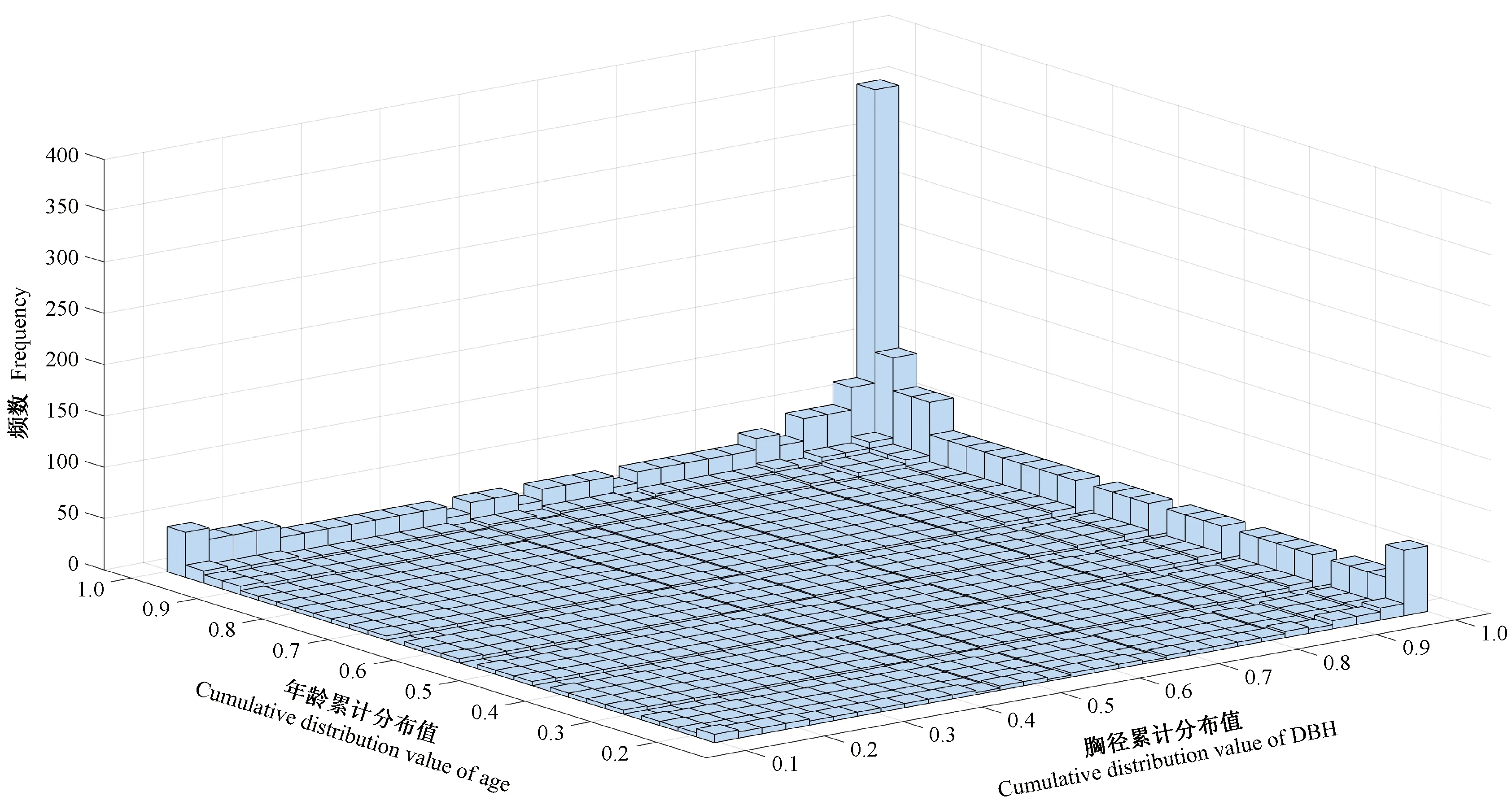
图1 毛竹胸径年龄累计分布的二维频数直方图Fig.1 The bivariate frequency histogram of cumulative distribution of DBH and age of moso bamboo

2.1.2 毛竹胸径年龄的二维Copula密度函数图 根据表1得出毛竹胸径和年龄的累计分布值，绘制毛竹胸径年龄各二元Copula联合密度图如图2所示。可以看出：1)二元Gumbel Copula和二元t-Copula联合密度图与图1接近，其他二元Copula联合密度图与图1存在较大差异，故优先选择二元Gumbel Copula和二元t-Copula密度函数测量毛竹胸径年龄联合分布；2)二元正态Copula、二元t-Copula和二元Frank Copula密度函数具有对称尾部，无法描述毛竹胸径年龄二元结构的非对称尾部相关性；二元Gumbel Copula密度函数具有非对称尾部，曲线呈J形，说明该函数对毛竹胸径年龄二元结构的上尾部变化较为敏感，能更好描述下尾低、上尾高的尾部相关性；二元Clayton Copula密度函数也具有非对称尾部，曲线呈L形，说明该函数对胸径年龄二元结构的下尾部变化较敏感，能更好地描述下尾高、上尾低的尾部相关性。

2.1.3 基于AIC的Copula函数优选 根据式(4)，计算二元t-Copula和二元Gumbel Copula密度函数的AIC分别为 -14.310 4和-19.519 6，确定系数(R2)分别为0.967 6和0.984 1，可见二元Gumbel Copula密度函数描述毛竹胸径年龄二元联合分布效果最好。

2.2 二元Gumbel Copula分布(密度)函数与常用二元分布(密度)函数的对比分析

以胸径和年龄的累计分布为自变量，采用极大似然法拟合二元Gumbel Copula密度函数参数α为1.055 0，R2=0.984 1，以胸径和年龄为自变量，拟合二元Weibull分布函数与二元Sbb密度函数参数分别为(a1,b1,c1,a2,b2,c2,r)=(-0.163 7,8.917 0,4.211 9,-1.192 6,3.573 4,3.506 2,1.003 2)和(ρ,ξ1,ξ2,λ1,λ2,γ1,γ2,δ1,δ2)=(0.082 5,1.903 1,-2.530 1,15.146 4,7.530 1,0.610 2,1.582 0,1.386 2,0.072 5)，R2分别为0.990 1和0.736 2。毛竹胸径年龄实测概率以及各概率密度函数的估计值如表2所示。

表2 实测概率以及二元Gumbel Copula(GumCp)密度函数、二元Weibull分布函数和二元Sbb密度函数估计值Tab.2 The measured probability and estimated values of the bivariate Gumbel Copula density function, the bivariate Weibull distribution function and the bivariate Sbb density function

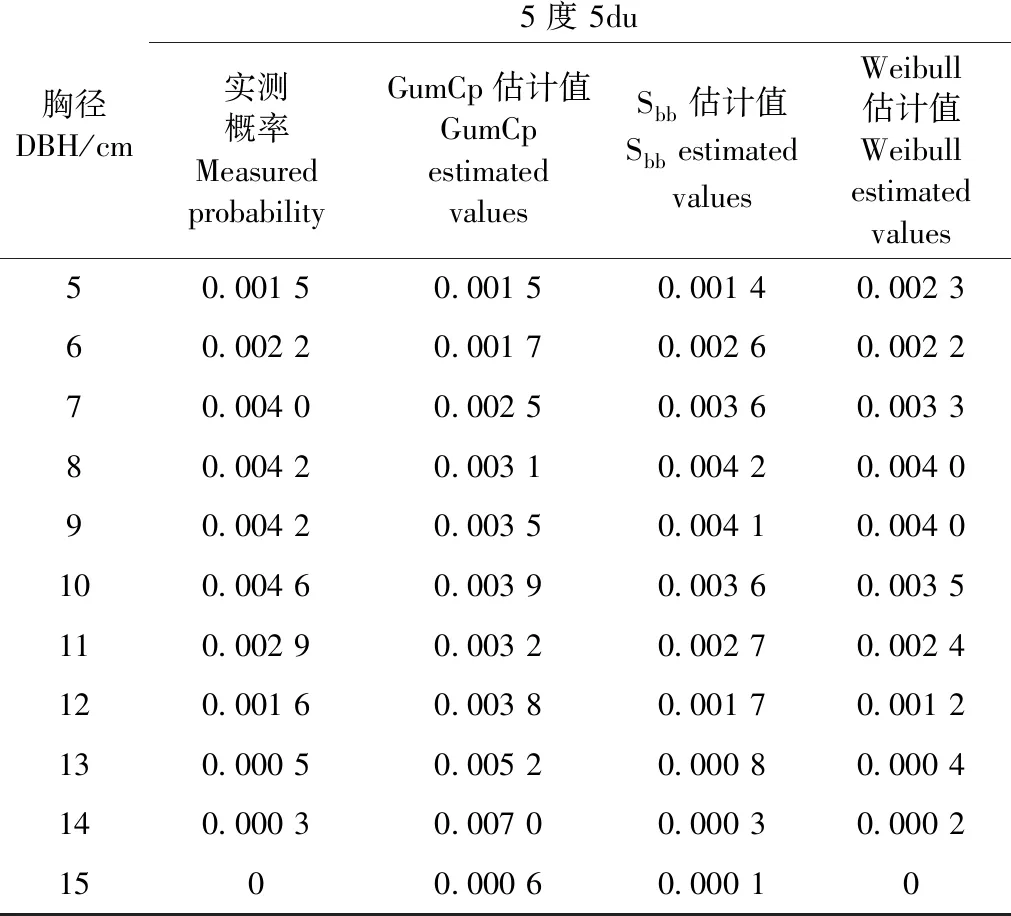
胸径DBH/cm5度 5du实测概率Measured probabilityGumCp估计值GumCp estimatedvaluesSbb估计值Sbb estimatedvaluesWeibull估计值Weibull estimatedvalues50.001 50.001 50.001 40.002 360.002 20.001 70.002 60.002 270.004 00.002 50.003 60.003 380.004 20.003 10.004 20.004 090.004 20.003 50.004 10.004 0100.004 60.003 90.003 60.003 5 110.002 90.003 20.002 70.002 4 120.001 60.003 80.001 70.001 2 130.000 50.005 20.000 80.000 4 140.000 30.007 00.000 30.000 21500.000 60.000 10

采用柯尔莫哥洛夫检验各分布(密度)函数的拟合优度(王岩等，2006)，此时二元Gumbel Copula密度函数、二元Weibull分布函数和二元Sbb密度函数累计值的最大偏差分别为D55,Copula=0.015 8、D55,Weibull=0.007 0、D55,Sbb=0.078 1，在0.05显著性水平下的阈值为D55,0.05=0.179 8，可见毛竹胸径年龄均服从这3种分布(密度)函数。

从表2可以看出：1)二元Weibull分布函数的测量精度比二元Gumbel Copula密度函数略高，二元Sbb密度函数测量精度最低；2)二元Weibull分布函数有7个参数，二元Sbb密度函数有9个参数，而二元Gumbel Copula密度函数只有1个参数，因参数越多越难收敛，故二元Gumbel Copula密度函数在估测精度非常高的情况下参数最易收敛；3)二元Weibull密度函数由分布函数求二阶偏导才能得到，导出的密度函数非常复杂，用二元Weibull分布函数估算森林结构特征因子二元概率密度时，首先要将原始数据变换成联合分布值，然后再将估算出的二元分布值变换成相应的联合密度值，联合密度值估算较繁琐，而用二元Gumbel Copula密度函数可直接得到森林结构特征因子二元概率密度的估计值，估测简单快捷；4)二元Gumbel Copula密度函数对小径阶、低龄级与大径阶、高龄级的测量值较实测值偏大，这也是该Copula密度函数本身固有的缺陷，混合Copula密度函数可克服这一缺陷，有关二元混合Copula函数的建模有待进一步研究。

2.3 毛竹胸径年龄二元概率密度图与二元Gumbel Copula分布图

根据表1得出毛竹胸径和年龄的边缘分布值，由式(1)计算毛竹胸径年龄二元Copula分布函数值，绘制图形如图3所示。可以看出：随着胸径和年龄累计分布值增大，毛竹胸径年龄联合分布值也增大，并在两边缘分布值取1和0时联合分布值达到最大和最小，与实际相符。

图3 毛竹胸径年龄二元Gumbel Copula分布函数图Fig.3 The joint distribution between DBH and age of moso bamboo using the bivariate Gumbel Copula distribution function

根据式(2)，可由毛竹胸径年龄二元Gumbel Copula分布函数推导出相应的二元密度函数，再根据式(3)，可计算毛竹胸径年龄二元密度值，以胸径和年龄边缘分布值为横轴和纵轴，胸径年龄二元密度值为竖轴，绘制图形如图4所示。可以看出：1)由于立地条件、人为经营等因素影响，毛竹胸径和年龄边缘分布值具有一定分布规律；2)毛竹胸径年龄二元密度值并不随胸径和年龄边缘分布值增大而增大，当胸径累计概率为0.664 6和0.999 8、年龄累计概率为0.824 2和0.973 8时，胸径年龄二元密度值达到最大和最小。

3 讨论

3.1 二元Copula分布(密度)函数与常用二元分布(密度)函数的比较

1)二者自变量不同：常用二元概率分布(密度)函数，如二元Weibull、二元Sbb、二元β分布函数等，其自变量为森林结构特征因子，因变量为对应的联合分布(密度)值，而二元Copula分布(密度)函数的自变量为森林结构特征因子的边缘分布函数值，因变量为对应的Copula连接函数值。

2)拟合参数所需条件不同：常用二元概率分布(密度)函数的参数拟合必须是森林结构特征因子实测数据的联合分布(密度)值，而二元Copula分布(密度)函数的参数拟合只需森林结构特征因子实测数据的边缘分布值，前者参数拟合所需条件比后者多，从侧面说明二元Copula分布(密度)函数适用性更广、实用性更强。

3)胸径与年龄边缘分布函数的类型：应用二元β分布(密度)函数拟合胸径年龄联合分布时，要求胸径和年龄的边缘分布函数类型必须为一元β分布(密度)函数，二元Weibull分布函数、二元Sbb密度函数也有类似要求，如果胸径和年龄边缘分布函数类型不同，则常用二元分布(密度)函数不适用，而二元Copula分布(密度)函数则适用于任意类型的胸径和年龄边缘分布函数。

4)联合分布函数的建立：常用二元分布(密度)函数不是由对应的边缘分布(密度)函数推导建立的(葛宏立等，2008；刘恩斌等，2010；Hafleyetal.，1976)，而无论在理论还是在实践中，森林结构特征因子边缘分布的类型众多且较容易确定，但其联合分布的价值较边缘分布更大，因此如何根据森林结构特征因子的边缘分布确定对应的联合分布意义重大。二元Copula分布(密度)函数通过连接胸径和年龄的边缘分布函数构建毛竹胸径年龄二元联合分布(密度)，为边缘分布推算对应的联合分布提供了一种可行方法。

5)模型的检验：实测森林结构特征因子的联合分布(密度)值是拟合常用二元概率分布(密度)函数参数必需的数据，为了检验实测数据是否服从指定的分布(密度)函数，需进行柯尔莫哥洛夫或卡方检验，而二元Copula分布(密度)函数的参数拟合只需森林结构特征因子的边缘分布函数值[不需要其联合分布(密度)值]，且在很多情况下，对于有些样本的实测联合分布(密度)值是得不到的，故AIC常被用来优选与检验二元Copula分布(密度)函数。

6)实现功能的比较：常用二元分布(密度)函数的功能是由两森林结构特征因子得到对应的联合分布(密度)值，二元Copula密度函数的功能是由两森林结构特征因子的分布函数值得到对应的Copula密度函数值，故常用二元分布(密度)函数图描述的是两森林结构特征因子的结构特征，而二元Copula密度函数图描述的是两森林结构特征因子的相关性特征(图2)。经变量相互转换，二元Copula分布(密度)函数可实现常用二元分布(密度)函数的功能，如设D为胸径，A为年龄，u=F(D)为胸径的边缘分布函数,v=G(A)为年龄的边缘分布函数，则由反函数D=F-1(u),A=G-1(v)可得对应的胸径和年龄值，由式(1)得胸径年龄二元Copula联合分布值就是毛竹胸径年龄二元联合分布值，与常用二元分布函数得出的胸径年龄联合分布值类似，以胸径和年龄为自变量，绘制毛竹胸径年龄的二元联合分布图如图5所示。可以看出：随着胸径和年龄增大，毛竹胸径年龄的累积分布值也增大，当胸径为5和15 cm、年龄为1和5度时，累计分布值分别取最小值和最大值，与实际相符。

以胸径和年龄为自变量，由式(3)得胸径年龄二元密度函数h(D,A)，绘制毛竹胸径年龄的二元联合密度图如图6所示。可以看出：1)胸径年龄二元密度函数值不随胸径和年龄取值增大而增大，当胸径为9和15 cm、年龄为3和2度时，其值为最大和最小；2)虽然对单株毛竹而言，其胸径和年龄的相关性不大，但由于立地条件和人为干扰等因素使省域尺度毛竹胸径年龄具有某种分布规律。

图6 毛竹胸径年龄的二元联合密度图Fig.6 The bivariate joint density of DBH and age of moso bamboo

3.2 森林结构特征因子的相关性

相关系数和偏相关系数常用来描述两森林结构特征因子之间的相关性(范叶青等，2013)，但其只能从线性角度进行描述，即两森林结构特征因子尾部与中间的相关性相等，当森林结构特征因子间的关系不能用线性函数描述时，则上尾部与下尾部的相关性可能不同，如从图2可知浙江省毛竹胸径和年龄的相关性上尾部较大、下尾部较小且渐趋于0，此时(偏)相关系数得出的结果是有误的，这也说明二元正态Copula密度函数不能描述毛竹胸径年龄分布的原因。

二元Gumbel Copula密度函数是毛竹胸径年龄的最优Copula密度函数，在此基础上，得出胸径和年龄Kendall秩相关系数为0.052 1、下尾相关系数为0、上尾相关系数为0.070 9、Pearson线性相关系数为0.000 0。

因毛竹独特的生物学特性，对单株毛竹而言，其胸径和年龄互不相关，但对省域尺度的毛竹而言，由于受立地因子、频繁经营等诸多不确定因素影响，使得省域尺度毛竹的胸径和年龄结构发生改变，从而使毛竹胸径和年龄存在某种复杂关系。Pearson相关系数的使用前提是假定毛竹胸径和年龄满足线性关系，显然不能反映胸径和年龄存在的这种复杂关系，故得出毛竹胸径和年龄不相关的结论不可靠。Kendall秩相关系数能反映两变量的变化趋势是否一致，故可以度量毛竹胸径和年龄的非线性复杂关系，毛竹胸径与年龄的Kendall秩相关系数为0.052 1，说明毛竹胸径和年龄的变化趋势一致，即随着毛竹林分年龄增大，林分胸径也在增大，这从上尾相关系数为0.070 9也能得到体现。

综上所述，二元Copula密度函数既能描述两森林结构特征因子的联合分布，也能客观反映两森林结构特征因子之间的相关性。

3.3 森林结构特征因子联合分布研究展望

本研究应用二元Copula分布(密度)函数探讨毛竹胸径年龄的二元联合分布，Copula分布(密度)函数对森林结构特征因子联合分布具有很大的应用价值，主要体现在以下4方面：1)使森林结构特征因子联合分布动态模型的建立成为可能，二元Copula分布(密度)函数的参数少，容易建立函数参数与时间t的函数关系；2)建立森林结构特征因子联合分布的混合概率模型，有些森林结构特征因子因受诸多因素影响，使得因子间存在复杂的尾部相关性，而不同二元Copula分布(密度)函数可以反映不同的尾部相关性，Copula分布(密度)函数混合即可全面描述森林结构特征因子间的这种复杂关系；3)使森林结构特征因子联合分布的研究范围大大拓宽，由于条件所限，只能获得两森林结构特征因子的实测边缘分布值，无法得到其实测联合分布(密度)值，在这种情况下，应用常用二元分布(密度)函数无法建立其联合分布模型，但使用二元Copula分布(密度)函数仍可研究其联合分布；4)本研究方法也可建立其他森林结构特征因子的联合分布(密度)模型，即，首先根据实测数据得森林结构特征因子的边缘分布值，然后确定最优Copula密度函数并拟合相应Copula密度函数的参数，最后建立森林结构特征因子的联合分布(密度)模型。

4 结论

1)二元Weibull分布函数的测量精度最高，R2=0.990 1，但其参数较多，迭代不易收敛，且在估算毛竹胸径年龄联合密度值时需进行数据相互转换，较为繁琐；二元 Sbb密度函数的测量精度最低，参数最多，R2=0.736 2；二元Gumbel Copula密度函数的测量精度也非常高，R2=0.984 1，只有1个参数，迭代过程非常容易收敛，估算联合密度时操作简单方便。

2)基于Copula分布(密度)函数建立毛竹胸径年龄二元分布模型的方法，适合于胸径和年龄的任意边缘分布函数，具体应用时，不需要确定边缘分布函数的类型，由实测数据得胸径和年龄的边缘分布函数值即Copula分布(密度)函数的自变量。

3)二元Gumbel Copula密度函数的 AIC为-19.519 6，为5个常用Copula密度函数中AIC最小的密度函数，是毛竹胸径年龄联合分布的最优Copula密度函数。

4)二元Gumbel Copula密度函数、二元Weibull分布函数和二元Sbb密度函数累计值的最大偏差分别为 0.015 8、0.007 0、0.078 1，在0.05显著性水平下的阈值为0.179 8，故毛竹胸径年龄联合分布均服从3种分布(密度)函数。

5)二元Copula分布(密度)函数较常用二元分布(密度)函数有较低的适用条件与较广的应用范围。