基于ARIMA 模型对全国农业受灾面积的数据分析与预测
2022-01-18李窈于丽婷
李窈 于丽婷
(大连民族大学,辽宁 大连 116600)
我国是一个拥有历史悠久的农耕文明的国家,随着时间推移经济发展,如今我国的耕地面积排在世界第三,农业人口约有三亿。由于特殊的地理条件,我国人多地少,局部地区的地理位置特殊,大多的大型农业设备无法投入使用,所以需要大量劳动力进行耕耘,这也导致了在自然灾害发生之后所带来的结果是可预见的。
要实现对灾情的管控,就要从根源上分析解决问题,防灾减灾工作的完善程度是重要的一环,灾后重建工作也是必须考虑到的问题。本文针对构造ARIMA 模型,预测未来1 年受灾面积的大小,为未来防灾减灾工作尽可能的提供帮助。
1 资料与方法
1.1 数据的收集,见表1。
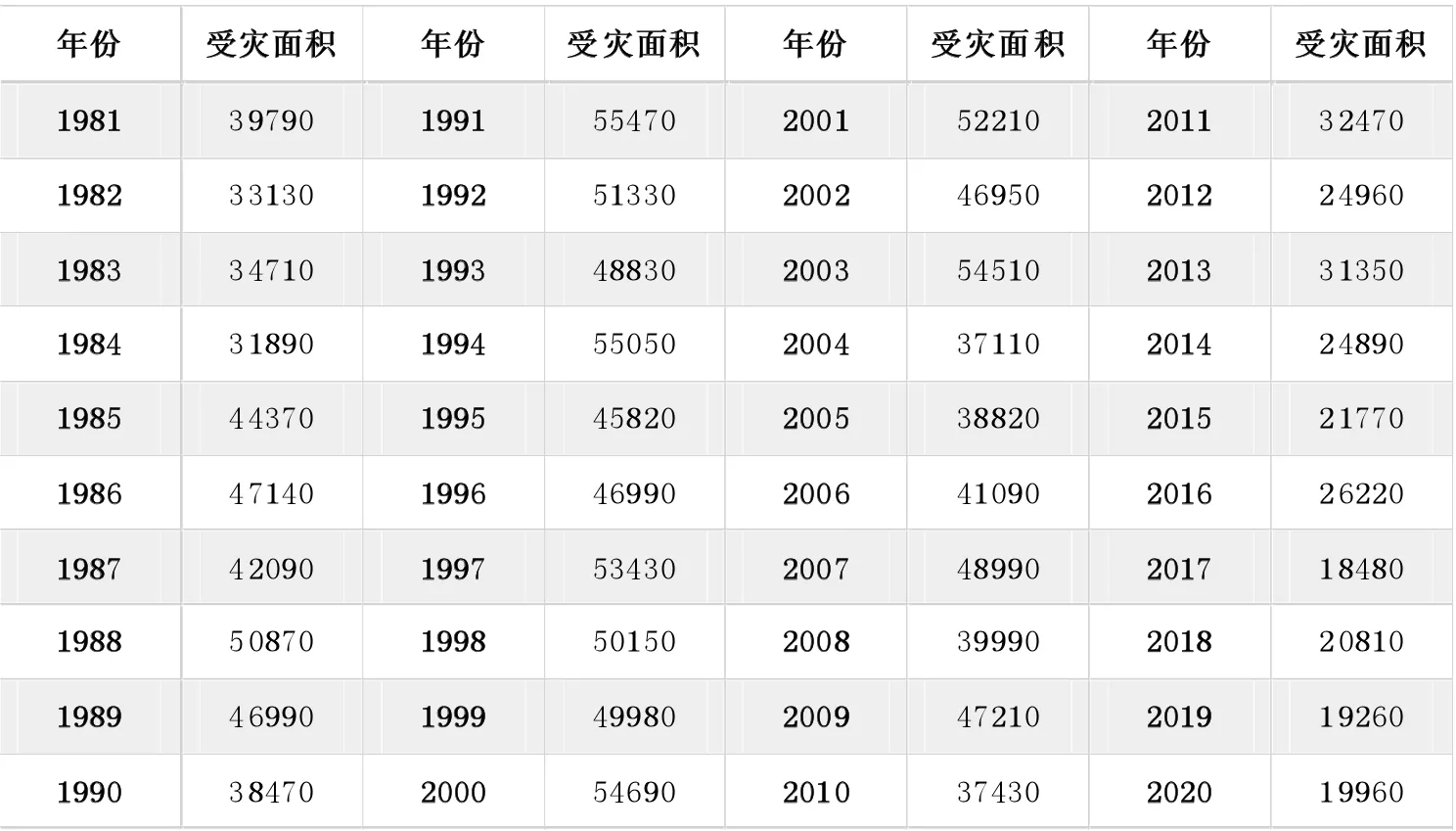
表1 农业受灾面积数据统计表 单位:千公顷
1.2 模型建立及数据分析
1.2.1 ARIMA 模型
去除不平稳的时间序列的趋势或者去除其局部水平以后会表现出序列一定的同质性。同时也就能知道这一类型的非平稳时间序列可以用差分处理将其转换为稳定的时间序列。这样的时间序列也被称为齐次非平稳时间序列。其中齐次的阶数是差分次数。

1.2.2 P 值介绍
需要测量样品观测数据和原假设假定的偏差值,要测量它的P 值。
如果原始假设是真的,则得到的样本结果会像实际观测结果那样极端或更加极端的概率被称为P 值。
P 值和原始假设是否正确的概率无关。只是一个与数据相关的概率。选择的是5%的显著性水平,如果原始假设是真的,这样的数据发生只有5%的可能性。P 值越小,说明实际观测到的数据与原假设之间的不一致程度越大,检验结果越显著。
在P 值已知的条件下,将与其给定的显著性水平α 值进行比较,就可以知道我们是否可以拒绝原假设。(下文中使用P值决策时,我们选择的是显著性水平为5%的情况,α 值为0.05,原假设为残差序列为不相关的序列)如果P 值<α,拒绝原假设;如果P 值>α,不拒绝原假设。
1.3 模型的建立
1.3.1 时间序列预处理
在绘制完序列的时序图后,需要观察序列是否为平稳序列。序列的自相关图是使用ACF 函数来描绘的,并且可以根据自相关图的具体情况来确定序列的稳定性。当自相关图中的自相关系数快速衰减到0 时,序列是平稳的,否则是不平稳的。
首先,由图1 可看出,农业的受灾面积近40 年来明显呈减少趋势,自相关图的自相关系数没有快速衰减为0,所以这个序列是不平稳的。因此,需要对序列进行差分提取,然后制作差分序列的时序图。
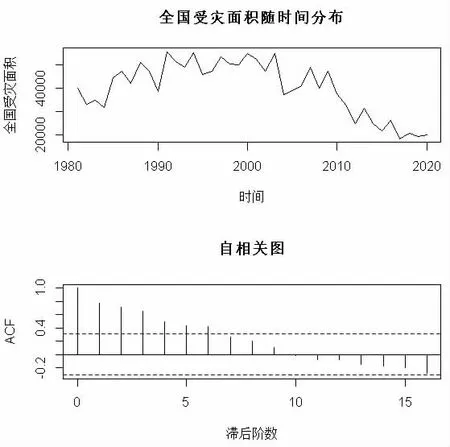
图1 全国受灾面积随时间分布图及自相关图
差分的主要目的是消除数据的变动,使数据处于稳定状态,更好的分析数据。如图2 的样本自相关函数图来看,从自相关函数延迟一阶之后,逐渐减小到两倍的标准偏差范围内。序列通过一阶差分后变得平稳,自相关图也表明自相关系数在一阶延迟之后迅速减少到0,也从另一方面验证序列是平稳的。
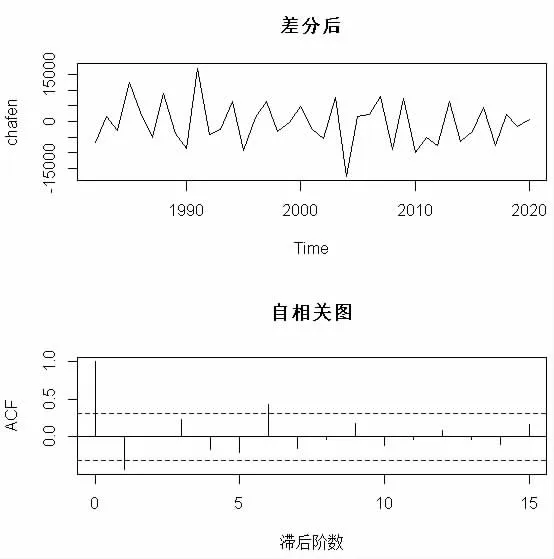
图2 差分后全国受灾面积随时间分布图及自相关图
1.3.2 模型识别及定阶
如表2 所示,可以使用ACF 图和PACF 图来判断模型的阶数。在图3 中,ACF 在lag=1 时截尾,即1 阶之后快速减为0,即q=1;PACF 在lag=0 时拖尾,即0 阶之后逐渐为0,即p=0,得到了模型为ARIMA(0,1,1)。

表2 模型的定阶原则
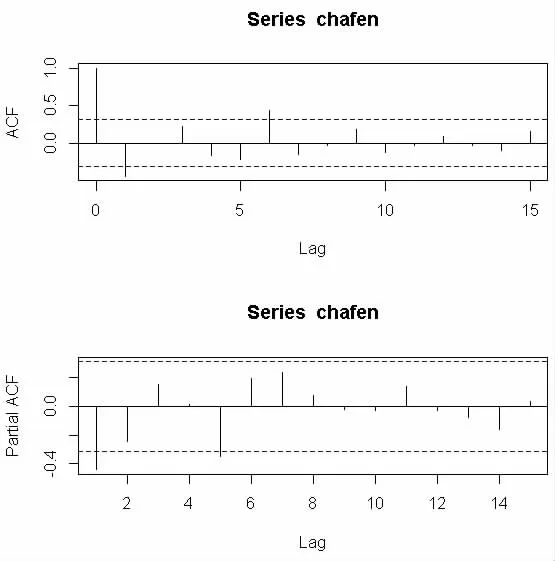
图3 差分后全国受灾面积自相关图和偏自相关图
2 结果检验及分析
2.1 模型检验
2.1.1 残差的正态性检验
可以根据残差QQ 图进行判断。如果QQ 图中的残差几乎分布在对角线附近,则与正态性假设一致。否则,模型中可能存在错误。
2.1.2 残差的无关性检验
根据白噪声定义可知,残差值等于估计值减去真实值,被检测序列应该是一个不相关的序列。得到残差后一般会使用LB统计量来检验残差。
R 语言运行程序得到LB 检验结果:p-value=0.5829
由图4 可知残差绝大多数都落在了对角线附近,说明结果符合正态性假设;因为P=0.5829>0.05,所以,我们没有理由拒绝原始假设,即残差序列是一个不相关序列。验证表明,残差序列通过了白噪声,并且模型的数据拟合充分,可以接着进行下一步预测。
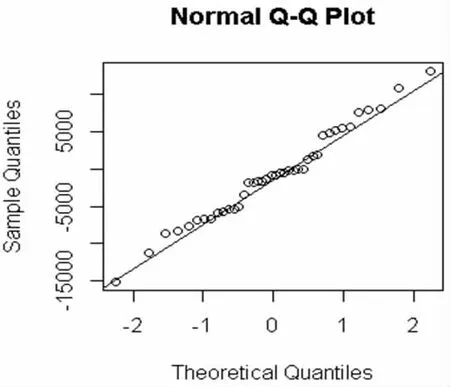
图4 残差QQ 图
2.2 预测
根据表3 结论,预测结果中自动给出了置信区间水平为80%和95%的置信区间,最终得到2021 年全国受灾面积预测值为200126.76 千公顷,如图5。

表3 2021 年全国受灾面积预测值表
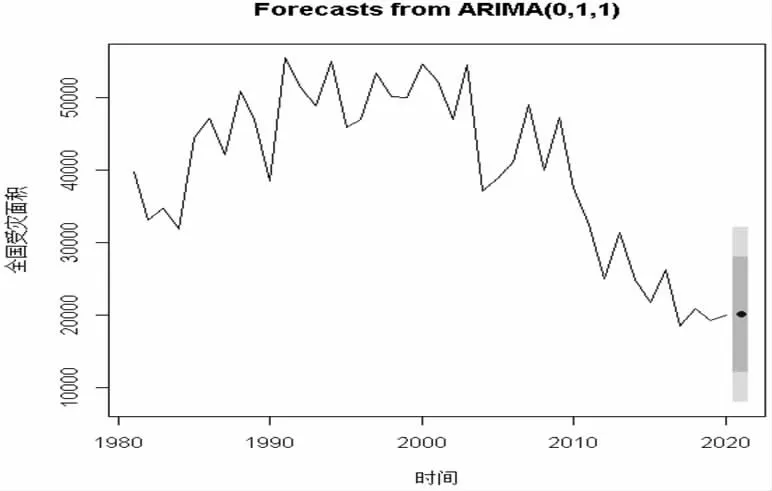
图5 2021 年全国受灾面积预测图
2.3 预测效果检验
我们用ARIMA 模型相应的程序对2018-2020 作了滚动预测, 即用2017 年以前的数据预测2018 年的值;用2018 年以前的数据预测2019 年的值;用2019 年以前的数据预测2020 的值。3 年平均绝对预测误差为4.79%,误差相对较小,可使用该模型对2021 年全国受灾面积进行预测,见表4。
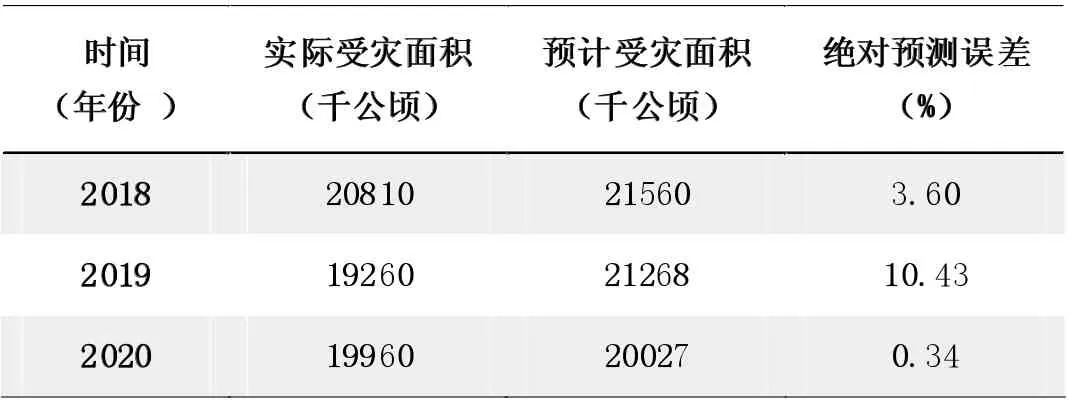
表4 用ARIMA 方法对近3 年的滚动预测结果
3 结论与讨论
3.1 本文运用了统计学时间序列下的ARIMA 模型进行预测,通过收集大量数据进行整合分析,建立数学模型并检验,最后进行预测,并将预测结果检验后得出绝对误差在11%以内,可信度较高。
3.2 在全球气候变暖、各种灾害频发的大环境下,我国也是世界上受自然灾害影响比较严重的国家之一,特别近几年来旱灾、水灾、台风频发,因此预测未来农业受灾面积的走势也可以对农业灾害方面的防治有帮助。
3.3 我们可以多关注天气预报,了解气候的变化规律,依据规律合理规划农事活动。及时清理积水,加强排水系统的管理,调整农业结构。掌握温度规律,合理搭配农作物品种、安排播种期,可以选择抗性较强的作物。
