智能头盔抗电磁干扰性能的非线性建模研究

张旭东，周年荣，唐立军

（云南电网有限责任公司电力科学研究院，云南 昆明 650217）

0 前言

随着电子技术、通信技术、传感器技术不断的融合和发展，出现了智能头盔，其在许多领域得到了成功的应用，如：煤矿井下信息采集，其可以对瓦斯浓度进行采集和实时分析，如果瓦斯浓度超过临界值，就会报警[1-3]。然而在智能头盔的实际应用中，外界电磁会对其进行干扰，影响其对信息采集和正常工作，智能头盔抗电磁干扰性能是一项评价其质量的重要标准。对智能头盔抗电磁干扰性能进行建模和估计具有十分重要的实际应用价值[4-6]。

针对智能头盔抗电磁干扰性能建模问题，一些发达国家投入大量人力和财力进行研究，而且研究的时间相当长，对智能头盔抗电磁干扰性能建模的技术相当成熟，而对国内由于对智能头盔出现的时间比较短，对智能头盔抗电磁干扰性能相关研究的文献比较少，还有许多难题有待攻克[7-9]。智能头盔抗电磁干扰性能的建模当前主要采用线性方法，如多元线性回性、时间序列分析法等，它们对智能头盔抗电磁干扰性能历史数据进行挖掘，描述智能头盔抗电磁干扰性能的变化特点，由于智能头盔抗电磁干扰性能具有强烈非线性，没有考虑该变化特点，使得智能头盔抗电磁干扰性能建模效果差，无法获得令人相信的智能头盔抗电磁干扰性能建模结果[10]。

1 抗电磁干扰性能的非线性建模

1.1 抗电磁干扰性能建模学习样本的构建

设采集的原始智能头盔抗电磁干扰性能数据为：X={xi,i=1,2..,n}，由于它们根据时间先后的顺序进行采集和整理，因此可以看作是一个时间序列数据集合，n表示数据点的数量，由于智能头盔抗电磁干扰性能数据由于其它因素的影响，这要使得它们的变化特点比较复杂，表面上看没有什么变化规律，但是进行深层次分析可以发现存在一定的变化规律，即混沌变化特点，因此需要引入混沌分析算法对智能头盔抗电磁干扰性能数据进行重建，建立智能头盔抗电磁干扰性能建模的学习样本。通过混沌分析算法确定嵌入维(m)和延迟时间(τ)，得到一个与原始智能头盔抗电磁干扰性能数据变化特点相同的多维数据，即：

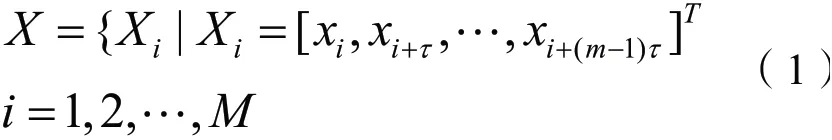
m和τ值的设置十分重要，直接决定了智能头盔抗电磁干扰性能建模效果，本文选择关联积分方法确定m和τ，以重建智能头盔抗电磁干扰性能数据。关联积分计算公式：

式中，θ(x)的计算公式为：

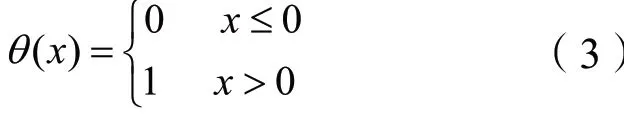
智能头盔抗电磁干扰性能数据序列的检验统计量计算公式为：

将其进行细分产生多个子序列，那么会有：

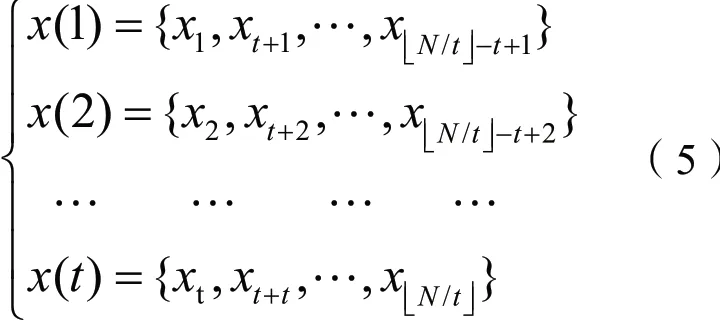
根据分块算法对式(5)的统计量进行计算，得到：

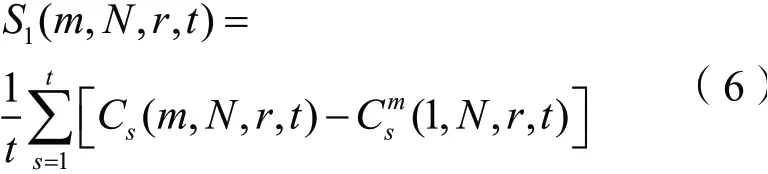
式中，r为两个智能头盔抗电磁干扰性能数据点之间距离。

当智能头盔抗电磁干扰性能数据序列相空间点数N无限大时，那么式(6)就可以简化为

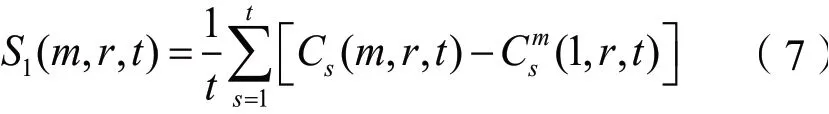
计算最大值和和最小值点的偏差，具体为：

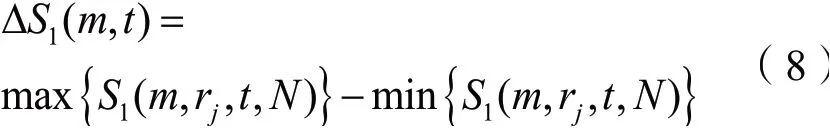
当ΔS1(m,t)为了个极小值点时，就可以得到最优的τ。

基于BDS(Brock Dechert Scheinkman)得到：

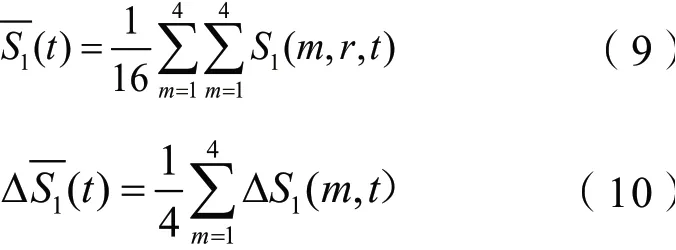
得到最优的m和τ值，根据m和τ值重建智能头盔抗电磁干扰性能数据，从而产生了智能头盔抗电磁干扰性能建模学习样本，然后引入BP神经网络建立智能头盔抗电磁干扰性能分析模型。

1.2 抗电磁干扰性能分析模型

1.2.1 BP神经网络算法

BP神经网络是一种具有良好建模性能的数据挖掘技术，其模拟人大脑的神经网络工作机制，其包括多层结构，最为经典的是3层，每一层包括了大量的神经元节点，同一个层的神经元节点没有什么直接关联，各相邻层之间的神经元节点互相关联。

1.2.2 BP神经网络的工作步骤程

根据式(13)和(14)可以得到隐含层和输出层的神经元输出。

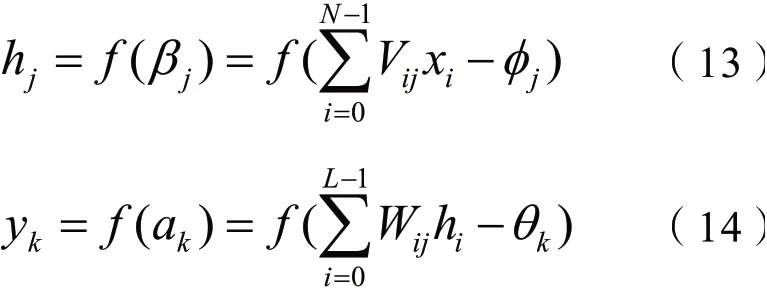
Step2：计算yk和dk之间的偏差，那么得多个输出偏差项：

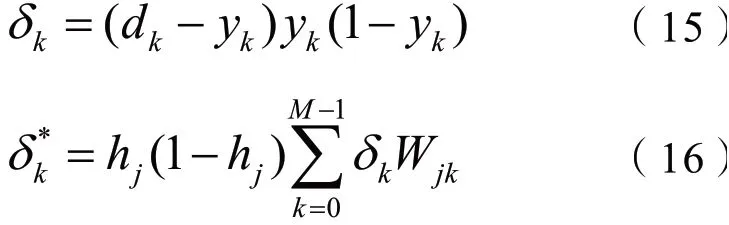
Step3：如果输出偏差大于实际要求，那么采用式(17)和(18)对各神经网络间的权重进行调节。

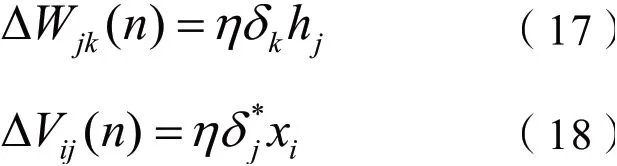
式中，η为神经网络的学习速率。

Step4：计算公调节后的各神经网络之间的权重值，具体如下：

Step5：不断重述步骤，直接到输出层的误差实际应用要求。

1.3 BP神经网络建立智能头盔抗电磁干扰性能分析步骤

Step1：采集一个智能头盔一段时间的抗电磁干扰性能数据。

写好书，体现的是“基础工作”建设的核心内容，也是老干部工作的总体任务。换言之，叫做“基础工作建设，从写书开始”。那么，要写什么样的书呢？目标是要写一本有特色的书。这个特色主要体现在以下五个方面。

Step2：引入混沌分析算法确定智能头盔抗电磁干扰性能数据重建的最优m和τ。

Step3：基于最优m和τ的值，建立一个多的智能头盔抗电磁干扰性能数据，即智能头盔抗电磁干扰性能分析的学习样本。

Step4：根据智能头盔抗电磁干扰性能分析的学习样本设计BP神经网络的结构。

Step5：初始BP神经网络的隐层的神经元与输入、输出层的神经元权重值以及阈值。

Step6：采用智能头盔抗电磁干扰性能分析的学习样本训练BP神经网络。

Step7：根据训练好的BP神经网络建立智能头盔抗电磁干扰性能分析模型。

智能头盔抗电磁干扰性能的非线性建模流程如图1所示。

图1 智能头盔抗电磁干扰性能的非线性建模流程

2 抗电磁干扰性能的非线性建模仿真

2.1 测试数据

为了测试智能头盔抗电磁干扰性能的非线性建模方法的有效性，选择5个智能头盔的抗电磁干扰数据作为实验对象，针对每一个智能头盔，采集一段时间抗电磁干扰数据，数据分布如表1所示。选择线性建模方法：多元线性回性、时间序列分析法进行对比实验。

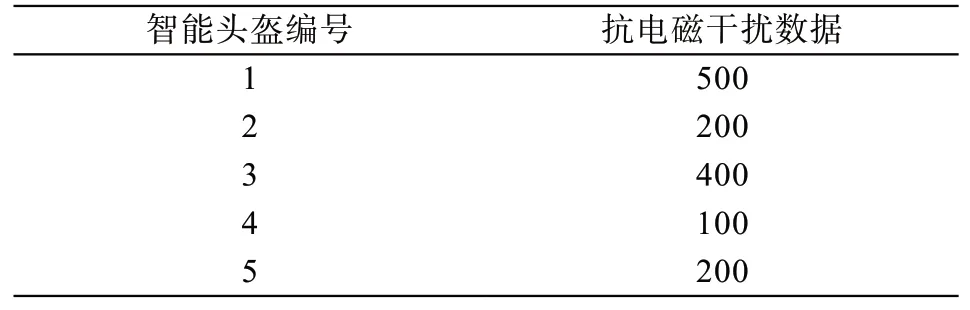
表1 5个智能头盔的抗电磁干扰数据分布

2.2 测试数据的嵌入维和时间延迟

采用混沌分析算法，确定表1中5个智能头盔的抗电磁干扰数据的嵌入维和时间延迟，具体如表2所示。根据表2的结果建立智能头盔抗电磁干扰性能数据学习样本。

表2 测试数据的嵌入维和时间延迟

2.3 结果与分析

采用本文方法和多元线性回性、时间序列分析法对5个智能头盔的抗电磁干扰性能的学习样本进行建模和分析，统计它们的单步分析精度，结果如图2所示。从图2的单步分析精度可看出：

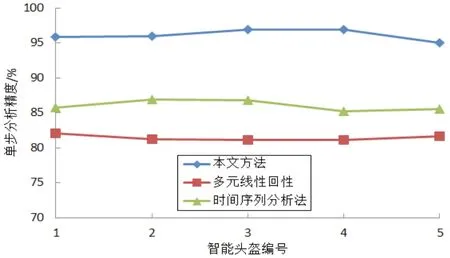
图2 智能头盔的抗电磁干扰性能单步分析精度

1）多元线性回性、时间序列分析法的智能头盔的抗电磁干扰性能单步分析精度均低于88%，智能头盔的抗电磁干扰性能分析误差比较大，无任何实际应用价值，这是因为它们无法描述智能头盔的抗电磁干扰变化态势。

2）本文方法的智能头盔的抗电磁干扰性能单步分析精度高于95%，智能头盔的抗电磁干扰性能分析误差大幅度减少，这是因为本文方法引入混沌分析方法对智能头盔的抗电磁干扰数据进行重建模，并引入BP神经网络刻画智能头盔的抗电磁干扰变化态势，建立了更优的智能头盔的抗电磁干扰性能分析模型。

由于智能头盔的抗电磁干扰性能单步分析结果只能描述下一个时间点的抗电磁干扰性能，在实际应用单步分析结果更具有价值，因此统计智能头盔的抗电磁干扰性能多步分析精度，结果如图3所示。从图3可知，本文方法的智能头盔的抗电磁干扰性能多步分析精度同样高于多元线性回性、时间序列分析法，这表明，本文方法可以对将来一段时间的智能头盔的抗电磁干扰性能进行有效描述。

图3 智能头盔的抗电磁干扰性能单步分析精度

3 结束语

为了获提高智能头盔抗电磁干扰性能预测精度，提出一种智能头盔抗电磁干扰性能的非线性建模方法，仿真实验结果表明，本文方法是一种精度高、误差小的智能头盔抗电磁干扰性能建模技术。