外加变位磁场作用GTAW 焊接电弧的数值模拟

周祥曼 刘 练 陈永清 袁有录 田启华 杜义贤 何青松 付君健

（1.三峡大学 机械与动力学院, 湖北 宜昌 443002；2.水电机械设备设计与维护湖北省重点实验室（三峡大学）, 湖北 宜昌 443002）

钨极惰性气体保护焊(gas tungsten arc welding,GTAW)是指在惰性气体保护下,利用阴极(钨极)和阳极(工件)之间产生的电弧熔化填充焊丝和母材的一种焊接方法.GTAW 的电弧稳定、焊缝美观且质量高,因此在航空航天、国防军工、轨道交通等领域有非常广阔的应用[1-2].

外加磁场作用作为焊接过程中一种非常重要的辅助手段,可以改变焊接电弧与熔池的传热传质过程,进而改善焊缝的质量.为此,国内外学者们对外加磁场调控焊接电弧行为开展了大量的研究工作.Ando等[3]探索了外加横向磁场改善TIG 焊缝成形的机理,研究结果表明,外加横向磁场能够使焊接电弧向前倾斜,加强了熔池内液态金属向前流动的趋势,从而达到改善焊缝质量的目的.周祥曼等[4]建立了基于GMAW 电弧增材成形过程中电弧和熔池的弱耦合模型,并揭示了外加横向磁场对电弧增材成形过程中电弧和熔池传热传质以及成形件微观组织影响的内在机理.刘海华等[5]建立了微束等离子电弧三维模型,并分析了外加横向稳态磁场作用下电弧特性与电弧对工件热、力输入的变化规律.卢振洋等[6]揭示了外加交变横向磁场作用下TIG 焊接电弧的运动机制,结果表明,外加横向交变磁场能使TIG 焊接电弧做有规律的交替进行的旋转运动和偏移运动.Melnikova T S和Prokalov V V[7]采用参数法和测量法研究了外加纵向磁场作用持续增压的非对称非稳态电弧等离子体温度场的局部参数,研究结果表明,电弧温度等值线的形状取决于电弧燃烧区域中心轴线的位移值.刘政军等[8]建立了基于磁流体动力学的二维轴对称的数学模型,分析了外加纵向磁场作用下的焊接电弧传热与流动特性.肖磊等[9]建立了外加高频纵向磁场作用下GTAW 焊接电弧的三维稳态数值模型,并解释了外加高频纵向磁场作用下的电弧收缩现象.常云龙等[10]通过研究外加纵向磁场对CO2焊接过程产生的影响,对比分析了不同磁场参数作用下的焊接电弧形态.

虽然国内外学者对外加磁场作用焊接电弧的研究较多,但大多局限于外加横向磁场和纵向磁场对焊接电弧的影响.基于此,本文提出一种兼具纵向和横向分量的外加变位磁场作用于焊接电弧,并利用FLUENT 软件建立纯氩保护的GTAW 电弧熔积过程的电弧模型,系统分析外加变位磁场作用下GTAW 焊接电弧的形态以及传热传质规律,为今后磁控焊接及磁控电弧增材技术的应用提供理论基础.

1 数学模型

1.1 基本假设

1)焊接电弧满足局域热平衡假设和光学薄的假设[11]；

2)忽略金属蒸汽对电弧的影响[12],电弧的流动状态为层流[13]；

3)在一个标准大气压下,保护气体(纯氩气)的密度、比热、热导率、黏度、电导率仅为温度的函数[9].

1.2 控制方程

本文描述电弧等离子体的控制方程为磁流体动力学数学模型,该模型已经在作者前期的研究工作[11,14]中做了详细的解释说明,故不再详细叙述.

1.3 物理模型和边界条件

本文建立的物理模型如图1所示.

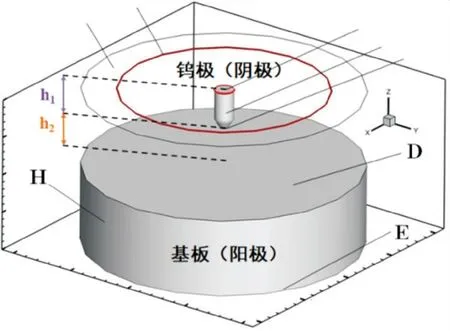
图1 电弧的物理模型

图中:阳极(基板)厚度为6 mm；阴极(钨极)直径为1.4 mm；下底面C直径为0.6 mm,尖角为60°；钨极的整体高度h1为3 mm,钨极固定不移动；电弧计算区域高度h2为3 mm；保护气入口F直径为15 mm；焊接电流为170 A；保护气为纯氩气,其流量为15 L/min,纯氩气的物性参数参考文献[14]；阴极的材料为钨,阳极的材料为SUS304 不锈钢,钨和SUS304不锈钢的物性参数参考文献[15].

表1为本文电弧模型的边界条件.

表1 电弧模型边界条件

其中,在钨极的上顶面A处设置焊接电流密度边界条件,基板底部E处设置为零电势边界条件,F处为氩气入口边界.焊接电流击穿G区域氩气,在阴阳两极之间气相区域放电产生电弧.保护气入口F的速度与气流量以及保护气喷嘴内径有关[11],相关公式见式(1):

式中:hconv为金属与空气的对流换热系数；Tamb为环境温度；α为斯蒂芬波尔兹曼常数；ε为辐射发射率[14].

2 外加变位磁场的施加方式

外加变位磁场是一种偏离竖直方向一定角度的磁场,即具有横向和纵向磁场分量的一种磁场.本文施加变位磁场的强度为0.005 T,外加变位磁场的施加方式以及对电弧整体作用力分析示意图如图2所示.其中B表示本文所施加变位磁场的磁通密度的大小和方向；BZ表示磁通密度B的Z向分量；BY表示磁通密度B的Y向分量；β表示变位角度；J表示电弧区域中电弧的电流密度；J1为电流密度矢量J的Z向分量；J2为电流密度矢量J的径向分量；Fm1表示磁通密度B的横向分量BY所产生的电磁力,即Fm1＝J1×BY,该电磁力会使电弧整体偏向一侧；Fm2表示磁通密度B的纵向分量BZ所产生的电磁力,即Fm2＝J2×BZ,该电磁力会使电弧整体受到沿顺时针方向的周向电磁力作用.

图2 外加变位磁场的施加及电弧受力分析示意图

3 模拟结果及分析

3.1 无外加磁场作用下的电弧云图

图3为无外加磁场作用下的Z＝7.5 mm 截面的电弧电磁力矢量分布图,可以看到电磁力矢量分布呈现对称并且有向电弧中心聚集的趋势.

图3 无外加磁场作用下Z＝7.5 mm截面电弧电磁力矢量分布

图4为无外加磁场作用下电弧温度为10 000 K的等值曲面图.可以发现电弧呈现周向完全对称,这是由于在平面基板情况下,电弧空间、边界条件均对称,电流密度和电磁力分布对称.

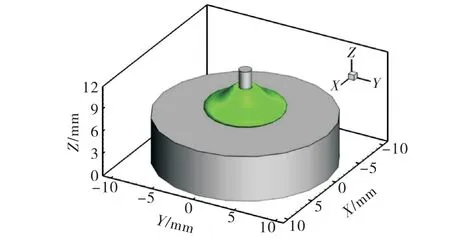
图4 无外加磁场作用时电弧温度10 000 K 等值曲面图

图5和图6分别为无外加磁场作用下XZ(Y＝0)截面的电弧压强分布和电弧温度场分布.可以看到电弧压强云图呈现对称且形似“秤砣”状分布,电弧温度云图呈现对称且形似“锅盖”状分布,电弧温度和压强最大值均出现在钨极下方,这是由于电弧的电流在此处聚集,电流密度最大,电磁力最大且向中心挤压形成的.图7所示为在相同弧长与电流的条件下,电弧模拟所得的等温线分布与参考文献[16]的实验测量所得的等温线结果对比,可以发现模拟结果与实验总体契合,从而验证了本文模型的有效性.

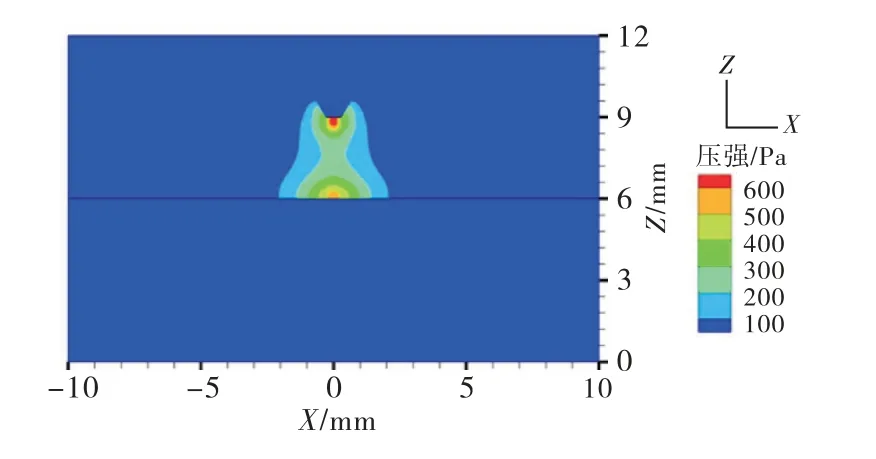
图5 无外加磁场作用时电弧压强分布云图

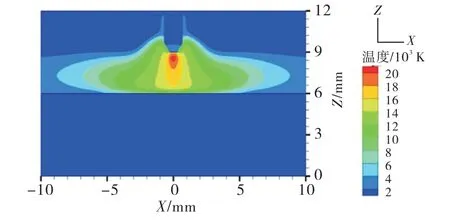
图6 无外加磁场作用时电弧温度场云图

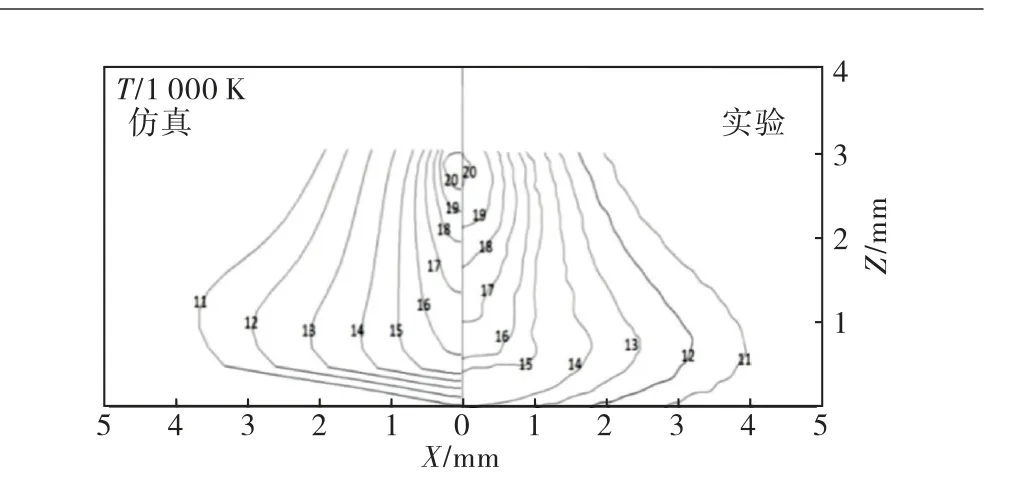
图7 电弧的等温线与实验结果[16]对比(单位:1 000 K)

3.2 外加变位磁场作用下的电弧模拟结果对比分析

图8为外加变位磁场作用下的Z＝7.5 mm 截面的电弧电磁力矢量分布图.可以看到,在外加变位磁场作用下,电弧电磁力矢量不再呈现对称分布,四周的电磁力不再指向中心.此外随着变位角度的增加,电磁力指向的位置偏离中心越来越远,电磁力偏转的角度越来越大.这是由于随着变位角度的增加,外加变位磁场的横向分量BY逐渐增大,纵向分量BZ逐渐减小,横向分量BY产生的指向—X方向的电磁力分量逐渐增大,纵向分量BZ产生的沿顺时针方向的周向电磁力分量逐渐减小,电弧同时受到指向—X方向的电磁“推力”作用和沿顺时针方向的“周向搅拌”电磁力作用,形成了如图8所示的指向—X方向和周向电磁力合力的分布效果,且随着变位角度的增加,电弧中心逐渐偏离轴中心,且往“第二象限”内偏转.

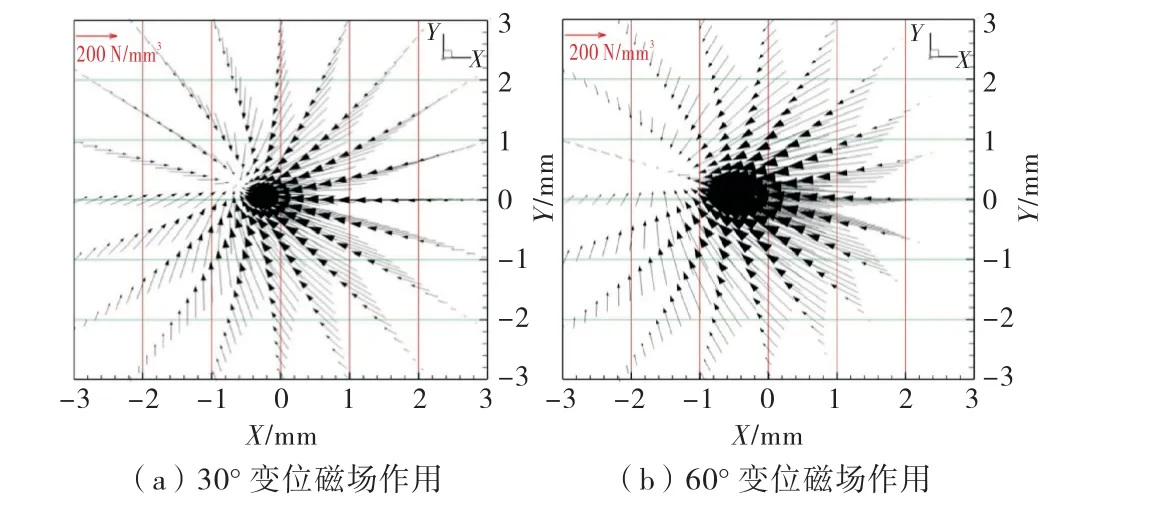
图8 外加变位磁场作用下Z＝7.5 mm 截面的电弧电磁力矢量分布图

如图9所示,外加变位磁场作用下的电弧温度为10 000 K 等值面不再呈现对称分布,随着变位角度的增加,电弧偏向—X方向越明显,并且电弧温度等值面在Y方向上收缩的趋势变得愈加明显.这是由于外加变位磁场的横向分量产生的指向—X方向电磁推力导致温度等值曲面向—X方向偏转,外加变位磁场的纵向分量产生的外加“搅拌”电磁力以及横向磁场产生的指向—X方向外加电磁“推力”使电弧所受的电磁力合力方向发生了偏转并且电磁力合力在Y方向上的分量也逐渐增大,这与图8所示XY截面(Z＝7.5 mm 截面)的电磁力分布相印证.

图9 外加变位磁场作用下的电弧温度为10 000 K 等值面图

图10和图11分别为外加变位磁场作用下的电弧压强分布云图和电弧温度分布云图.可以看到在外加变位磁场的作用下,电弧压强云图和电弧温度云图不再呈现对称分布,都偏向—X一侧,并且随着变位角度的增加,电弧压强分布和电弧温度分布偏向—X方向越明显.这是由于随着变位角度的增加,电磁力的分布呈现如图8分布的态势,即指向—X方向的电磁力逐渐增大,而周向电磁力逐渐减小,电磁力的综合作用使电弧等离子体逐渐向—X方向偏转.

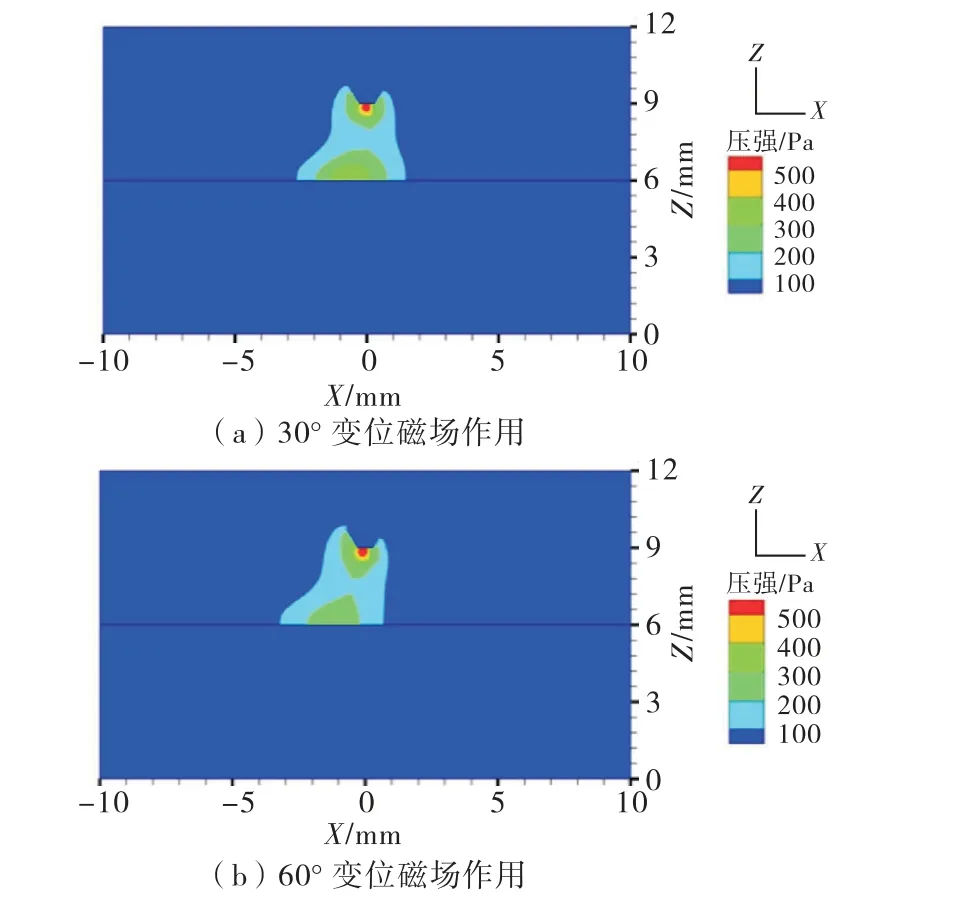
图10 外加变位磁场作用下电弧压强分布云图

图11 外加变位磁场作用下电弧温度场云图

4 路径分析

为了定量对比分析电弧各个参量的分布,本文在模拟空间取如图12所示的路径Path1(X方向,高度方向位于阴阳两极之间的正中间,P1(—10 mm,0 mm,7.5 mm),P2(10 mm,0 mm,7.5 mm)).Path1上的电弧参量分布如图13所示.

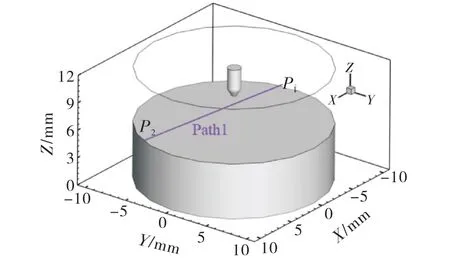
图12 路径选取示意图

如图13(a)、(b)所示,外加变位磁场作用下的电流密度和电弧温度均向—X方向偏移,电流密度和电弧温度峰值均小于无外加磁场作用时的情况且变化规律一致.这是由于电弧热由焦耳热主导,随着变位角度的增加,磁通密度在Y方向上的分量逐渐增大,Z方向上的分量逐渐减小,指向—X方向上的“电磁推力”逐渐增大,沿顺时针方向的“搅拌电磁力”逐渐减小,电弧逐渐向—X方向偏转.随着变位角度的增加,电弧弧柱向—X方向偏转程度越来越大,在Path1上电弧温度和电流的密度峰值也会逐渐降低.

如图13(c)所示,外加变位磁场作用下X方向电磁力分量的“波峰”逐渐上移,右边的“波谷”逐渐下移,且“拐点”位置逐渐向—X方向移动.这是由于随着变位角度的增加,“电磁推力”逐渐增大,指向—X方向的电磁力逐渐增大,指向+X方向的电磁力逐渐减小.如图13(d)所示,外加变位磁场作用下,Path1上的Y方向电磁力分量随着变位角度的增加逐渐从0变为双峰分布,再变为单峰分布,且左边的“波峰”峰值呈现逐渐增大的趋势,这是由于沿顺时针方向的“电磁搅拌力”作用,指向+X方向的电磁力向+Y方向偏转,指向—X方向的电磁力向—Y方向偏转,随着变位角度的增加,“电磁搅拌力”减弱、指向—X方向“电磁推力”增强使得指向+X方向电磁力向+Y方向偏转的角度增大,指向—X方向电磁力向—Y方向偏转的角度减小,即在Path1上指向+X方向的电磁力的Y向分量逐渐增大,指向—X方向的电磁力的Y向分量逐渐减小到0.

如图13(e)所示,在外加变位磁场作用下电弧压强逐渐向—X方向偏移,且峰值小于无外加磁场作用下的情况.这是由于无外加磁场作用下,电磁力呈现对称且具有向轴中心聚集的趋势,电弧等离子体在轴中心处所受挤压力最大,压强峰值最大,而在外加变位磁场作用时,在Path1上指向—X方向的电磁力大于指向+X方向电磁力,且电磁力向Y方向偏转,故电弧等离子体之间的碰撞减弱,压强峰值降低.

如图13(f)所示,外加变位磁场作用下,Path1上的X方向速度分量逐渐从类似余弦函数分布变为“单峰”分布,且“波谷”位置逐渐下移.这是由于随着变位角度的增加,Path1上指向—X方向的电磁力逐渐增大,指向+X方向的电磁力逐渐减小,从而导致指向+X方向的电弧速度X方向分量逐渐减小到0,指向—X方向的电弧速度X方向分量逐渐增大.如图13(g)所示,在外加变位磁场作用下,Path1上的电弧Y方向速度分量逐渐从0变为类似正弦函数分布,且“波峰”逐渐下移,“波谷”逐渐上移.这是由于无外加磁场作用时,电弧速度在Path1上呈现左右对称且具有从电弧中心向外发散的趋势,Y方向的速度分量为0.而随着变位角度的增加,沿顺时针方向的“电磁搅拌力”减弱,指向—X方向的“电磁推力”逐渐增强,导致在Path1指向—X方向的电弧速度向+Y方向,指向+X方向的电弧速度向—Y方向偏转的角度均减小,即指向—X方向的电弧速度在+Y方向速度分量、指向+X方向的电弧速度在—Y方向的速度分量均降低.

图13 Path1上的电弧各个参量对比

5 结 论

1)外加变位磁场产生的沿顺时针方向的“搅拌电磁力”作用和指向—X方向的“电磁推力”使得电弧形态不再呈现对称分布.

2)外加变位磁场作用焊接电弧使得Path1上的X方向电磁力分量“波峰”上移、“波谷”下移；电弧Y方向电磁力分量由0变为“双峰分布”,再变为“单峰分布”,且“波峰”上移；电弧X方向速度分量由类似余弦函数分布逐渐变为“单峰”分布,且“波谷”下移；电弧Y方向速度分量由0逐渐变为类似正弦函数分布,且“波峰”下移,“波谷”上移.