加工及装配误差对气体轴承运动状态的影响规律*

李勇德 何永熹 刘检华

(北京理工大学机械与车辆学院 北京 100081)

气体轴承具有摩阻极低、转速高以及环境适应性好等优点，在高速旋转机械中获得了广泛应用[1-2]。气体轴承具有多种类型，其中动静压气体轴承具有启动特性好、不易磨损、稳定性高等特点[3-5]。气体轴承间隙很小，有较高的加工、装配精度要求[6]。在旋转机械中，不对中是导致转子失稳的重要原因，而加工与装配误差则是造成轴承不对中的主要因素[7]。

针对加工与装配误差对气体轴承性能的影响，国内外多位学者进行了相关研究。任天明等[8]研究了加工误差对H型动压气体轴承刚度的影响，结果表明，0.2 μm的气膜误差会导致气膜刚度降低20%以上。边新孝等[9]研究了加工误差对气体静压轴承承载能力的影响，发现轴承间隙误差为平均气膜间隙的5%时，承载力可产生约10%的变化。姚英学等[10]利用相容性变换条件，研究了制造误差对气体承静态特性的影响，发现误差对气体轴承径向承载能力影响较大。PANDE等[11]基于二维可压缩黏性流的Reynolds方程计算了表面粗糙形貌对静压轴承静态特性的影响。STOUT[12]采用类似的数值分析方法研究了轴承间隙等制造误差对轴承静态特性的影响。CROSBY[13]分析了静压轴承静态特性受椭圆圆度误差与表面粗糙度的影响规律。赵琪等人[14]研究了制造误差造成的轴颈偏斜对轴承性能的影响，发现轴颈偏斜距离变化对轴承性能影响较大，偏斜角度对轴承性能影响较小。但现阶段所做的加工与装配误差对气体轴承运动状态影响的研究多采用以Reynolds润滑方程为基础的数值分析方法，对分析动静压耦合效应误差较大[15]，并且大都为对轴承稳态特性的求解，而对轴承的动态特性问题涉及较少。贾晨辉等[16]采用商业软件FLUENT研究了动静压气体轴承的运动状态随转速变化的规律，发现转子的振动幅度随转速的增加呈现先减小后增大的状态，并指出由于气体轴承转速极高，轴承气膜的变化是非线性过程，因此以气膜为研究对象是研究气体轴承稳定性的关键。

本文作者以螺旋槽动静压气体轴承气膜为研究对象，基于计算流体力学与六自由度耦合方法，采用流体仿真软件FLUENT模拟转子在运转过程中的轴心轨迹，通过分析轴心轨迹及其频谱特征，研究加工和装配误差对动静压气体轴承运动状态的影响规律。研究结果为动静压气体轴承设计、加工与装配精度的确定提供理论依据。

1 气膜模型

1.1 球面螺旋槽动静压气体轴承结构

球面螺旋槽动静压气体轴承的结构简图如图1(a)所示，主要由两部分组成：带有螺旋槽的转子以及带有供气孔的定子。为了简化计算，建立的气膜模型如图1(b)所示，尺寸参数如表1所示。

图1 球面螺旋槽动静压气体轴承Fig 1 A hybrid bearing with spherical spiral grooves (a)the schematicof structure;(b)three-dimensional model of the gas film

1.2 网格划分与边界条件

由于气体轴承气膜厚度很薄，并且需要考虑到由制造、装配误差产生的细微尺寸变化，故采用网格划分软件Pointwise对气膜模型进行网格划分。Pointwise具有极高的尺寸识别以及拟合精度，对于处理复杂细小尺寸几何模型具有独特优势。为检验所用网格分辨率得到的仿真结果的收敛性，对无加工及装配误差的理想模型进行网格无关性检验，测试网格总量分别为90万、120万与150万，网格划分如图2所示。其中对无供气孔区域实施结构化网格剖分，对供气孔与气膜交接处实施六面体与四面体混合网格剖分。图3所示为3种不同网格分辨率下的幅频图。结果表明，随着网格分辨率的提高，轴心轨迹幅值差异在减小，而且120万网格分辨率得到的轴心轨迹幅值相较于150万得到的结果差异已经很小。综合考虑计算精度与计算成本，文中后续仿真均采用网格总量约为120万的分辨率进行模型计算。

图2 气膜网格划分示意Fig 2 Mesh of the gas film of the hybrid bearing

图3 不同网格分辨率下的轴心运动轨迹幅频图Fig 3 Amplitude-frequency graph of the axis orbitfor three different grid resolutions

对气体轴承进行瞬态流体动力学仿真时的边界条件为：(1)轴承两端气膜的大端口与小端口均为出气口，并且出气口处气压为101.3 kPa(1个大气压)；(2)供气孔端面为压力进口，供气压力为稳定的0.2 MPa，气体为氦气，黏度为2×10-5Pa·s，且考虑为可压缩流体；(3)其余边界条件为壁面边界条件，其中内壁面为旋转的刚性壁面，外壁面为固定壁面。

1.3 流体润滑理论

对螺旋槽动静压气体轴承动态特性的仿真过程中，其流体模型主要考虑连续性方程以及动量守恒方程，由于润滑气体在流动过程中气体能量交换较小，故不考虑能量守恒。另外，由于气体在轴承气膜内存在较大的压力变化，需要考虑气体的可压缩性，故为使模型方程封闭，还需要引入气体状态方程。

气体轴承的模型域内无质量源项，其非稳态连续性方程为

(1)

式中：ρ为流体密度；t为流体流动时间；u为流体矢量场。

针对文中研究的气体轴承，其流体为氦气，可以考虑为牛顿流体，且重力作用对气膜内流体的运动影响很小，可以忽略。采用FLUENT中k-εRealizable湍流模型计算气膜流动，其动量方程与湍动能方程为

(2)

另外，边界层选择FLUENT中的标准边界层函数。

对于完全气体，其3个基本状态参数压力p、密度ρ和温度T满足状态方程：

p=ρRT

(3)

式中：T为绝对温度；R为气体常数。

1.4 6DOF理论

工程中可根据物体的运动状态将问题分为2种，一种是运动状态已知的问题，称之为主动运动，另一种是运动状态未知的被动运动。在气体轴承中转子运动，既受到电磁力矩作用，又受到周围气体的作用，而文中关心的转子的质心运动主要受周围气体的作用力的影响，而转子的运动又会影响到气膜结构，进而影响气膜内的流体运动，因此这是一个双向耦合问题，也是被动运动问题。FLUENT中的6DOF(六自由度)模型主要用于模拟计算域中存在运动的刚体的流固耦合问题。

惯性坐标系下刚体结构的重心平移运动的控制方程为

(4)

式中：v为质心的平移速度矢量；m为物体质量；fG为周围流体作用在刚体界面上的外力矢量。

在体坐标系下刚体旋转运动的控制方程为

(5)

式中:ωB为刚体在体坐标系下旋转运动的角速度矢量；L为惯性张量；MB为刚体的力矩矢量。

将以惯性坐标系表达的MG转化为以体坐标系表达，形式如下：

MB=RMG

(6)

其中变换矩阵：

(7)

式中:Cχ=cosχ，Sχ=sinχ，χ为θ、φ、ψ；角θ、φ、ψ分别为绕x、y、z轴旋转的欧拉角。

另外，惯性坐标系中，刚体受到的周围流体合力矩：MG=∑r×fG。

2 仿真结果与讨论

文中分别对球面螺旋槽动静压气体轴承为理想状态(无加工与装配误差)，定子存在对中误差，以及定子存在尺寸误差等几种不同情况下的转子轴心轨迹的动态行为进行分析。

2.1 理想状态分析

在无加工与装配误差的理想情况下，不同转速下转子轴心轨迹图和频谱图分别如图4、图5所示。当转速为10 000 r/min时轴心轨迹由大到小逐渐稳定在较小的椭圆范围内，振幅最高时为0.014 μm(见图4(a)、图5(a))。当转速为20 000 r/min时轴心轨迹依旧由大到小稳定在较小的椭圆范围内，但椭圆长短轴长度有所提升，振幅最高时为0.038 μm(见图4(b)、图5(b))。当转速为30 000 r/min时轴心轨迹一直稳定在较大的椭圆范围内，振幅最高时为0.087 μm(见图4(c)、图5(c))。当转速为40 000 r/min时轴心轨迹发散，转子不能达到稳定状态(见图4(d)、图5(d))。

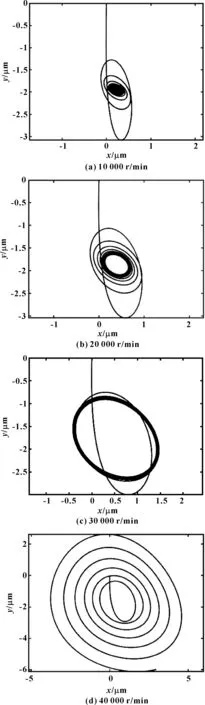
图4 不同转速下转子轴心轨迹图Fig 4 Axis orbits of rotor at revolving speed of 10 000r/min(a),20 000 r/min(b),30 000 r/min(c) and 40 000 r/min(d)

图5 不同转速下转子频谱图Fig 5 Spectrograms of rotor at revolving speed of 10 000r/min(a),20 000 r/min(b),30 000 r/min(c) and 40 000 r/min(d)

图6所示为转子振幅随转速的变化关系，可以看出，随着转子转速增加，转子振幅逐渐增大。另外，从图4可以看出，随着转子转速增加，轴心轨迹从稳定在较小的椭圆轨迹中演变为较大的椭圆轨迹，随着转速继续上升轴心轨迹发散；当转速在临界转速30 000 r/min时，轴承运行状态稳定，轴心轨迹为规则的椭圆形，当转速达到40 000 r/min时，轴承稳定状态被破坏，轴心轨迹发散，轴承处于失稳状态。文献[17]针对气体轴承转子动力学分析得到了类似的结论，虽然具体结构和转速有所差异，但是所得转子轴心轨迹随转速的变化规律是一致的。

图6 无误差时转子转速-幅值曲线Fig 6 Rotor revolving speed-amplituderesponse curves without error

2.2 定子轴线偏移

轴承装配过程中，由于定子两端球壳轴线不对中，一端定子轴线出现偏移，造成两端定子装配出现同轴度误差，如图7所示。

图7 轴线偏移误差模型Fig 7 Error model of axis offset

选取转速为10 000 、20 000、30 000 r/min，在轴线偏移距离h分别为0.5、1、2 μm情况下进行模拟仿真，得到其轴心运动轨迹，并提取频谱成分分析后，得到不同转速、不同偏移距离下的转子振幅变化，如图8(a)所示。可以看出：定子轴线偏移引起的转子幅值变化在低转速的情况下较小，轴承处于稳定运转的状态；当转子速度达到临界速度30 000 r/min时，转子振幅受定子轴线偏移影响较大；随着偏移误差增加，轴心轨迹从稳定在较小的椭圆轨迹到较大的椭圆轨迹再到极限环运动，如图8(b)所示，同时轴心轨迹中心点也随着偏移误差的出现向y轴负向偏移。

图8 转子幅值随轴线偏移距离变化及转子轴心轨迹Fig 8 Variation of the amplitude of rotor with axis offset androtor axis orbit (a)amplitude under different speedsand axis offsets;(b)axis orbit (30 000 r/min,axis offset 2 μm)

2.3 定子轴线倾斜

轴承装配过程中，由于定子两端球壳轴线不对中，一端定子轴线出现倾斜，造成两端定子装配出现同轴度误差，如图9所示。

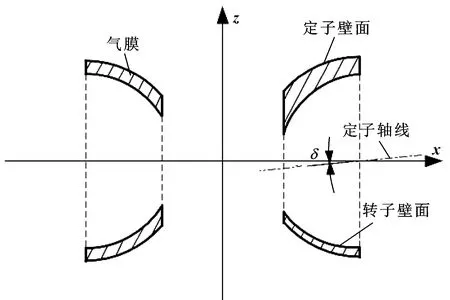
图9 轴线倾斜误差模型Fig 9 Error model of axis tilt

选取转速为10 000、20 000、30 000 r/min，在倾斜角度δ分别为0.5°、1°、2°情况下进行模拟仿真，得到其轴心运动轨迹，通过提取频谱成分分析，得到不同转速、不同倾斜角度下转子振幅的变化，如图10(a)所示。可以看出：定子轴线倾斜引起的幅值变化规律与轴线偏移类似，在低转速情况下影响较小；当转子速度达到临界速度30 000 r/min时，转子振幅受定子轴线倾斜影响较大。随着倾斜误差增加，轴心轨迹也是从稳定在较小的椭圆轨迹演变为极限环，如图10(b)所示，同时轴心轨迹中心点也随着偏移误差的出现向x轴正向偏移。

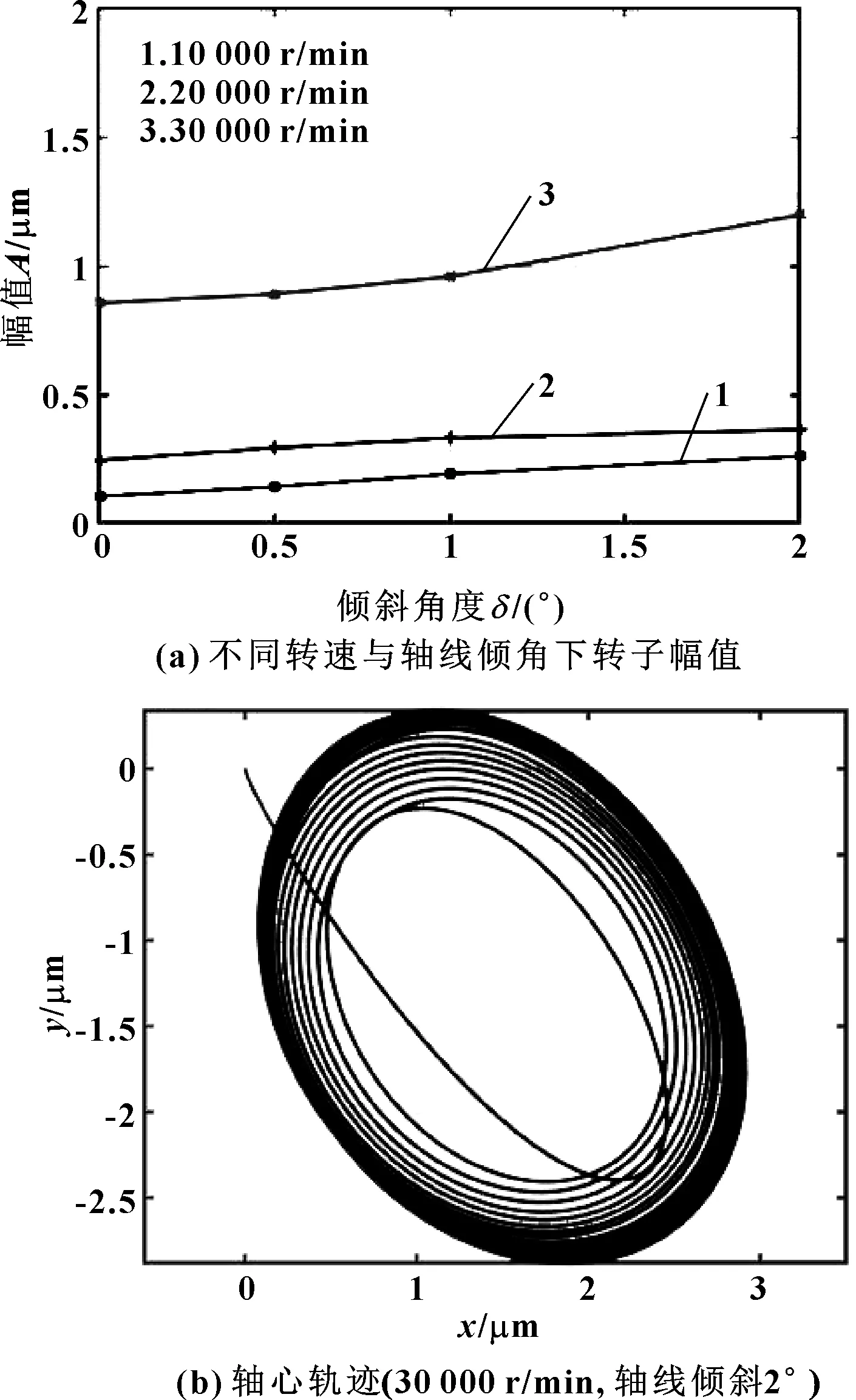
图10 转子幅值随轴线倾斜角度变化及转子轴心轨迹Fig 10 Variation of the amplitude of rotor with the tilting angleof the axis and rotor axis orbit (a) amplitude underdifferent speeds and tilting angle of the axis;(b)axis orbit (30 000 r/min,tilting angle 2°)

2.4 定子尺寸误差

轴承加工过程中，由于两端定子尺寸存在加工误差，导致两端气膜厚度不一致，如图11所示。

图11 定子尺寸误差模型Fig 11 Error model of stator dimension

选取转速为10 000、20 000、30 000 r/min时，在定子尺寸误差r分别为0.5、1、2 μm情况下进行模拟仿真，得到其轴心运动轨迹，并提取频谱成分分析后，得到不同转速、不同定子半径误差下的转子振幅变化，如图12(a)所示。可以看出：虽然存在定子半径误差，但由于单边气膜厚度仍然均匀，所以在所选转速范围以及尺寸误差范围内，转子振幅随着定子半径误差的增大仅发生小幅增大，对运动稳定性影响很小。只有当转速达到30 000 r/min，并且定子半径误差达到2 μm时转子振幅会有一定的提升，但轴心轨迹仍稳定在一定的椭圆范围内，如图12(b)所示。

图12 转子幅值随定子半径加工误差变化及转子轴心轨迹Fig 12 Variation of the amplitude of rotor with the radial errorand rotor axis orbit (a)amplitude under differentspeeds and radial errors;(b)axis orbit(30 000 r/min,radial error 2 μm)

2.5 粗糙度

通过在FLUENT软件中设置气膜两侧壁面粗糙度数值，模拟气体轴承在不同表面粗糙度下的运动状态。模拟计算时考虑粗糙度的影响，实际上是在湍流模型的壁面函数中包含了壁面粗糙度的影响。选取转速为10 000、20 000、30 000 r/min，在表面粗糙度分别为0.1、0.2、0.4 μm情况下进行模拟仿真，得到其轴心运动轨迹以及不同转速与表面粗糙度下轴心轨迹变化，如图13(a)所示。可以看出：在定子与转子表面粗糙度不超过0.4 μm时，转子振幅在较小的范围内上下波动，轴心轨迹均稳定在一定大小的椭圆内，如图13(b)所示，对定子运动稳定性影响较小。

图13 转子幅值随定子与转子表面粗糙度变化及转子轴心轨迹Fig 13 Variation of the amplitude of rotor with the surfaceroughness of the rotor and rotor axis orbit (a)amplitude under different speeds and surfaceroughness;(b)axis orbit (30 000r/min,roughness 0.4 μm)

3 结论

针对螺旋槽动静压气体轴承建立了CFD-6DOF流固耦合仿真模型，针对加工及装配误差对转子运动稳定性的影响进行了仿真分析，得到的主要结论如下：

(1)装配误差对轴承运动稳定性影响较大，当转速达到30 000 r/min，定子轴线偏移误差以及定子轴线倾斜误差分别达到2 μm以及2°时，转子振幅增加明显，轴承运动状态均为极限环运动，处于临界稳定状态。为保证气体轴承运动稳定性，应确保气体轴承的轴线装配精度。

(2)在保证轴承对中良好的情况下加工误差对轴承运动稳定性影响较小。当定子尺寸误差小于1 μm时，转子振幅增大的幅度较小，达到2 μm时，增幅略为明显；当表面粗糙度值不超过0.4 μm时，转子振幅在较小的范围内上下波动，轴承依然保持稳定。