基于多核学习支持向量机算法的隧道掘进速度预测

张海波 曹 科 刘鑫昌 宋康磊 张 帅

(1.中铁十八局集团有限公司, 天津 300222;2.重庆大学 土木工程学院, 重庆 400045)

盾构机因其自动化程度高、安全性强、施工进度快、对地面建筑物干扰较小、不受天气影响等优点被广泛应用.目前,盾构法已成为隧道施工的主要方式,尤其是对于城市地铁隧道和长隧道[1].盾构机虽然优势明显,但对地质条件十分敏感且成本较高,有效预测特定地质条件下盾构机性能对于施工方法选择、进度安排以及工程预算尤为重要,性能预测即对净掘进速度、施工速度、使用率和刀具磨损进行预测[2].

目前,国内外的科研工作者在掘进机性能预测方面做了很多的研究,经过不懈的努力,开发了很多种掘进机性能预测模型.在众多预测模型中,最著名的是CSM 模型[3]和NTNU 模型[4].CSM 模型由科罗拉多矿业学院的Rostami和Ozdemir提出,它基于大量完整岩石的全尺寸切割试验,综合考虑了岩石单轴抗压强度、抗拉强度以及滚刀特征等因素,为多变量回归方程;Yagiz引入了节理面角度、软弱层间距等指标,对CSM 模型进行了修正[5].NTNU 模型由挪威科技大学Bruland提出,它能够预测掘进速度、滚刀损耗及费用预算,由于其采用了多个岩石物理力学参数和机器性能参数,让模型使用较为复杂[6].此外,为了考虑复杂的围岩特性对隧道掘进的影响,Barton对岩体质量Q 分级系统进行改进,选用了多个参数,提出了QTBM 模型[7],用来预测隧道掘进机(TBM)的掘进速度.

近年来,机器学习异军突起,成为了解决复杂工程和科学问题的一大利器.Yagiz等将神经网络运用到掘进机性能预测中,建立的模型预测结果准确度有所提高[8];Grima等通过模糊神经网络建立了TBM掘进速度预测模型[9].Mahdevari等利用支持向量回归建立了一种TBM 掘进速度预测模型[10].Armaghani等建立了基于传统的人工神经网络和粒子群优化人工神经网络以及帝国竞争算法优化神经网络三种算法的TBM 掘进速度预测模型[11-12].然而神经网络模型是以传统统计学中样本无穷大时的渐进理论为基础的,在面对实际问题中有限的样本数据时往往难以取得较好的预测效果.此外,普通的支持向量机在核函数选择上也比较复杂,不能适应不同的问题.

本文将多核学习支持向量回归算法应用于地铁盾构机性能预测,前期通过收集整理深圳地铁10号线坂贝区间的地质勘察资料和盾构机掘进数据,经数据预处理组成本文的样本集,而后分别建立了支持向量回归(support vector regression,SVR)及多核学习支持向量回归(multiple kernel learning-Support Vector Regression,MKL-SVR)智能预测模型,将模型应用于预测盾构机净掘进速度,取得了良好的成效,对后续施工方法选择、进度安排以及工程预算等有重要参考意义.

1 支持向量回归基本原理

1.1 支持向量回归模型

SVM 是由Vapnik等人提出的一种机器学习算法[13-14].SVM 建立在VC 维(vapnik-chervonenkis dimension)理论和结构风险最小化准则基础上,基于最大化分类间隔的方法,首先提取位于类边界上的支持向量,然后利用这些支持向量来构造最优的分类超平面,该分类超平面能够保证数据点被错分的概率最小,在最小化样本点误差的同时,最小化结构风险,提高了模型的泛化能力.SVR 是在SVM 的基础上进一步延伸得到的,其核心是将SVR 问题转化为SVM问题[15-18],因其良好的性能而被广泛应用于回归或者预测等方面.

当SVR 用于线性回归时,其最优化问题的形式如下:

公式(3)是SVR 问题的一般表达式,通过SMO算法可以得到SVR 的决策函数为:

SVR 的核函数和核参数决定了模型的性能,如若选取不当,则性能较差,此外核函数所含核参数的数目过多时,因各个参数相互独立将会导致最优参数的选取极度困难.

线性核函数、多项式核函数、径向基核函数、sigmoid核函数是几种常用的核函数.线性核函数一般适用于简单的线性回归,多项式核因涉及参数太多,各参数相互独立,很难寻找参数的最佳组合,sigmoid核函数一般适用于大数据样本,而径向基核具有较好的兼容性,且参数数量合理,便于寻找最佳参数,是应用最广泛的核函数,所以结合本文数据数量以及复杂程度,选择径向基核作为支持向量回归机的核函数.

1.2 多核学习支持向量回归模型

虽然SVR 能够在非线性回归中变现良好,但由于核函数和核参数的选择十分困难,往往要依靠经验不断尝试才能找到相对较好的组合.此外,由于不同核函数有各自的擅长领域,在SVR 中只能选择对大多数数据表现良好的核函数,往往不能照顾到一些异构点[19].

为了解决上述问题,本节采用加权线性组合的方式将多个核函数融合,建立MKL-SVR 模型,解决了核函数选择的难题,融合后的核同时具有其组成核的性质,能够更好地适应样本中的异构点.

在多核学习中,核函数K(x,x′)由一系列基本的核函数组合而成:

采用梯度下降法来计算权值向量d,将J(d)对d m求偏导得:

通过公式(10),可以求得梯度下降方向D的各个元素,最终求得D;在得到梯度下降方向D之后,根据Simple MKL算法[20]来求得最优权值向量d;将d代入公式(5)以求出核函数K(x,x′);将K(x,x′)代入公式(6)可以将MKL-SVR 问题转化为SVR 问题求解,然后利用2.1节的求解方法进行求解.

2 应用实例

本文依托深圳地铁10号线坂田北路站至贝尔路站区间工程,该区间地质条件如图1所示.隧道穿越复合地层和孤石群,其中复合地层从上到下依次为砾质黏性土、全风化花岗岩、砂土状强风化花岗岩,孤石岩性为微风化花岗岩.地下水位埋深1.80～4.90 m,参照地区以往水位变化情况,地下水位的年平均变化幅度为0.5～2.0 m.根据地质勘察资料和盾构机掘进数据,从盾构机、土层和孤石3个维度共选取10个参数作为盾构机净掘进速度的影响因素,其中盾构机的掘进参数选取土仓压力、总推力、刀盘扭矩和刀盘转速,土层参数选取黏聚力、内摩擦角和压缩模量,另孤石参数选取孤石占比、抗压强度和岩石质量指标(rock quality designation,RQD),而后经数据预处理形成样本集.样本集中10个参数为输入变量,净掘进速度(penetration rate,PR)为输出变量,分别采用SVR 和MKL-SVR 模型对净掘进速度进行预测,并对两种模型的预测结果进行了对比分析.为了评估模型的性能,采用R2、均方根误差(root mean squared error,RMSE)作为评价指标.R2越接近1,证明模型相关性越强;RMSE越小,证明模型误差越小.

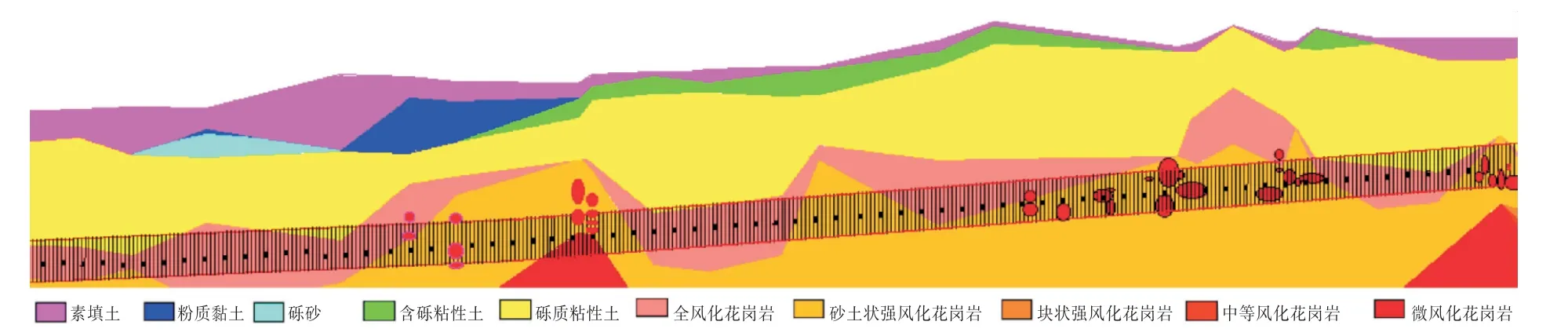
图1 局部地质剖面图

本文样本集总共包含503环的掘进数据,由于掘进速度与盾构机及地质条件相关,因此样本数据中包含这两个维度的相关参数.此外,隧道穿越孤石群会影响掘进速度,因此需要加入孤石相关参数.根据训练集和测试集划分的一般原则[21],将350 环(70%)数据设定为训练集,将余下的153组(30%)数据作为测试集.

2.1 SVR模型预测

SVR 的核参数直接影响其性能,本文选用径向基核作为SVR 的核函数,此时,SVM 模型中有两个参数需要确定,分别为惩罚参数C和核参数的gamma,其中惩罚参数C决定模型对于误差的容忍性,当C越大时,模型对误差的容忍程度越低,那么导致的结果就是模型欠拟合,当C越小时,模型对误差的容忍程度越高,那么此时模型的泛化能力将受到影响;gamma决定样本点在经过核函数映射后的分布,支持向量与gamma的值呈负相关.用SVR 模型进行计算时,首先要确定两个参数的值,本文的方法是在C、gamma组成的二维参数矩阵中,依次对每一对参数进行计算,从而寻求其最优值.在运行过程中,C、gamma相互独立,便于并行化运算,为了尽可能减少数据划分对结果产生的影响,采用网格搜索与k折交叉验证相结合的方式,把训练集拆分成k份,轮流将其中(k-1)份作为训练集,1份作为测试集,总计训练k次,取其平均值作为其最终结果,最终确定最佳参数C和gamma分别为4和22.627.采用SVR 模型进行PR 预测的结果如图2所示.

图2对比了实测值和SVR 模型的预测值,其中蓝色点表示实测值,红色点表示预测值.在训练集中,多数预测值与实际值较为接近,整体拟合效果较好.在测试集中,能够反映实测值的整体走势,但相对预测集而言,误差比较大.表1列出了此时SVR 模型的性能指标,模型在测试集和预测集的R2分别为0.928和0.777,训练集上各样本点比较靠拢拟合线,而在测试集上样本点分布比较散乱,所以模型在训练集上的表现很好,但在测试集上的表现略差,此时是因为模型出现了过度学习的情况,从而在测试集上预测效果不好.图3为SVR 模型相关性分析.

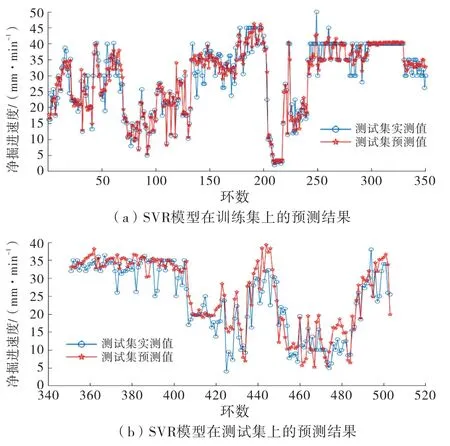
图2 SVR 模型在训练集和测试集上的预测结果

表1 SVR 模型性能指标

图3 SVR 模型相关性分析

2.2 MKL-SVR模型预测

本节采用加权线性组合的方式将多个核函数融合,建立MKL-SVR 模型,解决了核函数选择的难题,融合后的核同时具有其组成核的性质,能够更好地适应样本中的异构点.多核不但可以由多个不同的核函数融合而成,也可以由多个同一类型不同核参数的核函数组成.

MKL-SVR 的流程如图4所示,首先输入数据,选定所要进行多核融合的基础核函数,在基础核函数选择上,应选择涵盖面较广的多个基础核,由核函数将样本集映射到不同的特征空间,根据数据的适应度得出各个基础核函数在多核合成中占的权重,而后进行核函数的融合,建立MKL-SVR 模型进行回归预测并对其性能进行分析.

图4 MKL-SVR 流程图

在多核合成时,选用12参数不同径向基核和4个参数不同的多项式核进行组合,12个径向基核的gamma参数分别取0.01、0.1、0.5、1、2、5、8、10、13、15、17 和20,多项式核的gamma 参数设置为1,degree参数分别取1、2、3和4,训练5次,取其回归预测的平均值.

图5给出了MKL-SVR 模型的预测值和实测值对比,其中蓝色点表示实测值,红色点表示预测值.在训练集上,预测值能够很好地贴合实测值,整体走势一致;在测试集上,能够比较好地预测实测值,依旧存在个别突变点拟合不到位的情况.如图6所示,其中黑色点表示测试集数据,红色点表示预测集数据,可以看出两类点都比较贴合图中蓝色直线,表明预测结果与实测值误差不大.在预测集中,当净掘进速度较小时,相关性非常强,当净掘进速度在20～30 mm/min时,预测值误差增大;在测试集中,当净掘进速度在30 mm/min 以上时,误差较小,当净掘进速度在5～15 mm/min时,此时预测值误差略大,在实测值上下波动.

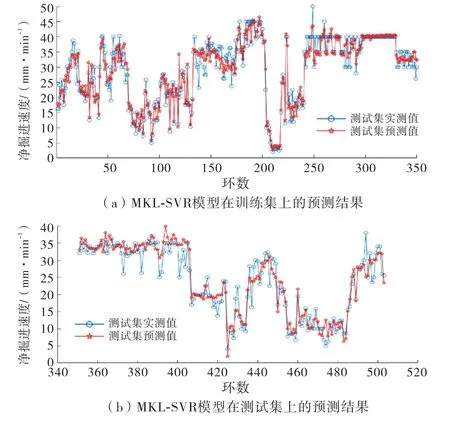
图5 MKL-SVR 模型在训练集和测试集上的预测结果

图6 MKL-SVR 模型预测值与实测值相关性分析

表2给出了MKL-SVR 模型在训练集和测试集上的性能指标.

表2 MKL-SVR 模型性能指标

2.3 两种预测模型的比较

表3 两种模型的性能对比

通过两种模型预测性能的对比,可以得出多个核函数融合的多核学习支持向量机模型在预测性能上要明显优于传统支持向量机.这是因为传统SVR 在核函数和核参数选择上十分困难,往往要依靠经验不断尝试才能找到相对较好的组合.由于不同核函数有各自的擅长领域,在SVR 中只能选择对大多数数据表现良好的核函数,往往不能照顾到一些异构点[19].本文采用加权线性组合的方式将多个核函数融合,建立MKL-SVR 模型,解决了核函数选择的难题,融合后的核函数可以兼具多种核函数的优点,能够更好地适应样本中的异构点,这正符合本文样本数据中有孤石数据的输入.此外,多核不但可以由多个不同的核函数融合而成,也可以由多个同一类型不同核参数的核函数组成,面对复杂多变的实际施工条件,可以灵活选用和融合核函数,以适应复杂的地质条件,具有很好的工程适用性.

3 结 论

本文提出了一种基于多核学习支持向量机算法的地铁盾构机净掘进速度预测模型,并利用深圳地铁10号线坂贝区间的数据验证了该模型的有效性,最终得出以下结论:

1)盾构机的掘进性能和地质条件、掘进及施工参数等因素相关,很难从理论上全面揭示其相关性.本文提出的MKL-SVR 模型能够拟合多种相关因素与掘进速度之间的非线性关系,有效预测掘进效率.

2)为了克服神经网络需要大量数据和SVR 核函数选择困难的缺点,首次将MKL-SVR 模型应用于盾构机净掘进速度预测,与已有模型相比,既增强了处理小数据量的能力又避免了核函数和核参数选择的负担,提高了模型的鲁棒性和泛化能力,在对样本集进行预测时,MKL-SVR 模型的R2达到了0.895,较SVR 模型的R2提高了0.118,MKL-SVR 模型在适应性和精确度方面较SVR 模型都有较大提高.