新建隧道下穿既有铁路的爆破振动控制标准研究

石伟民 何 方 陈士海 揭海荣 李海波

(1.华侨大学 土木工程学院, 福建 厦门 361021;2.中铁二十四局集团福建铁路建设有限公司,福州350013;3.中国科学院 武汉岩土力学研究所,武汉 430071)

在实际隧道工程建设中,由于场地和周边环境的限制,难免会使新建隧道通过下穿铁路结构等方式进行爆破开挖,在这种空间地层联系紧密的环境下进行爆破施工,极易因爆破产生振动而对既有铁路结构稳定产生威胁和影响,进而影响铁路结构的运营和安全[1].制定合理的振动控制标准,能将新建隧道爆破开挖对铁路结构产生的振动影响控制在安全和合理范围内,根据弹性力学波动理论[2],既有建筑物、构筑物受到的爆破拉、压应力主要受质点的振动速度、弹性模量、泊松比和密度的影响,而隧道爆破施工中,弹性模量、泊松比和密度是常量,因此可采用振动速度作为评价振动影响的控制指标.关于铁路振速控制标准的确定,爆破安全规程仅给出表1[3-4]一般施工环境下铁路路基的爆破振动安全允许值,显然对于下穿铁路工程爆破不具有适用性,因此有必要对下穿铁路工程爆破制定合理的振动控制标准.

表1 铁路路基爆破振动安全允许值

由于实际施工中无法进行破坏性试验来寻找安全振速和变形的临界值或极限值,而采用数值模拟能较好地预测和解决临界值问题.曹正龙[5]等以青岛地铁新建2、3号线区间隧道呈立体交叉状为工程背景,通过FLCA3D 动力模型分析验证当振动控制标准为5 cm/s时近距离交叠工程采用钻爆法施工是安全的;叶宇[6]等应用MIDAS/GTS-NX 对沪昆某铁路隧道下穿沪昆高速公路进行数值模拟,得出新建隧道与既有高速公路不同相对位置的峰值曲线变化规律;朱正国[7]等人以南京地铁超小净距隧道为工程背景,通过数值分析得出背爆侧峰值振动速度最大为4.8 cm/s;薛里[8]等人利用埋地管道材料的Von-Mises屈服准则确定爆炸荷载作用下管道的临界振动速度,并将临界振动速度标准设为190 mm/s;于建新[9]等对爆破施工开挖区进行爆破振动监测,计算得出走马岗地区爆破质点峰值振动速度(PPV)的Sadovsk公式,并反演出整个爆破振动控制范围内,振速控制在4.5 cm/s时能满足振动安全控制要求;袁良远[10]等结合现场实测数据与统计分析,理论计算出上行铁路隧道的爆破振动安全控制标准为8.0 cm/s;刘建友[11]等为对京张铁路左右到发线采用微振爆破跨主振周期,中洞采用干扰降振法,得出围岩及喷射混凝土的振动控制标准为37 cm/s、25 cm/s;胡英国[12]等为了确定岩石高边坡爆破振动控制标准,以上台阶振动允许最大振速和当前爆破梯段岩体损伤深度作为计算依据,通过理论计算和应力波衰减机制分析,结果表明振动安全标准的确定与允许开挖损伤深度、台阶高度等密切相关;刘建友[13]等采用经验总结法和理论分析法,建立振动波速与材料强度之间的关系,提出围岩与支护结构的爆破振动控制标准;曲云腾[14]通过在调研分析国内外不同使用功能建筑物的振动控制的基础上,预测了既有铁路站线的振动影响值.

上述学者对爆破振动控制标准的制定开展了一定研究,但基于铁路结构的安全性和敏感性高于一般建筑物,应结合铁路线路变形展开振动控制标准研究.目前根据铁路线路变形来制定振动控制标准的研究较少,本文从铁路线路水平、高低、路基受振变形保护角度出发,提出以铁路线路变形作为爆破振动控制标准的计算依据展开研究.对于下穿铁路爆破施工的振动控制标准研究,多数研究仅建立在一般性爆破安全规范和依托于类似的工程案例进行分析,并没有明确和严格的理论计算依据.本文将铁路轨道结构和铁路路基看成整体柔性结构进行变形分析,通过数值分析,探究爆破振动对铁路结构水平、高低和路基变形的影响程度,得出路基变形是爆破振动后铁路线路的主要变形方式,最后给出本工程的铁路结构振动控制标准,为下穿铁路工程爆破提供一定的借鉴和指导.

1 下穿铁路爆破振动控制标准计算依据确定

1.1 铁路线路保护要求

隧道下穿既有铁路爆破开挖时,爆破振动将使铁路结构发生形变,铁路结构变形的主要方式是轨道的水平、高低变位以及铁路路基的沉降变形.表2[15]给出一般爆破施工环境下铁路结构水平、高低及路基变形的控制值.表2给出铁路结构在一般爆破施工环境下的线路变形保护要求,而下穿铁路路基的变行沉降可以通过沉降槽计算近一步论证其沉降控制值.

表2 轨道动态几何不平顺容许偏差管理值

1.2 下穿铁路路基沉降变形控制值确定

下穿铁路路基由爆破振动引起的沉降并不等同于一般铁路路基的工后沉降,路基工后沉降多为均匀沉降,而下穿工程引起的路基沉降多呈U 型漏斗状[16],如图1所示.

图1 地铁隧道施工地面沉降槽

由于铁路轨道结构和路基联系紧密,为方便后续计算和开展研究,将铁路轨道结构和铁路路基整体看成柔性结构进行变形分析,将铁路路基的沉降变形等效为轨道结构整体沉降变形.

设地表允许沉降控制标准为Smax,则考虑回归系数后Smax可表示为:

其中:F为最大等效应力,取值见表3,a1～a5均为回归系数,取值见表4[17].

表3 最大等效应力

表4 回归系数

路基沉降计算可以根据Peck地表沉降理论计算得到,其中沉降槽宽度系数i与隧道埋深H关系,可采用式2[17]表示:

其中:Z为地表到隧道中心的距离;φ为隧道周围地层内摩擦角.

由Peck公式[17-18]可知,沉降曲线反弯点处的地面沉降量等于隧道中心线上方地面最大沉降的60%,将x=i带入得反弯点处沉降量为

设路基的允许最大沉降值为S路基根据Peck 沉降槽理论得,地面沉降槽10 m 弦长的最大沉降等同于路基沉降值,则可得路基沉降允许值与地面最大沉降的关系:

2 下穿铁路爆破振动控制标准的工程应用

2.1 工程概况

以厦门市地铁3号线区间隧道建设为工程背景,区间隧道左线DK9+546.773～DK10+085.000,总长538.227 m,右线DK9+546.773～DK10+086.000,总长539.227 m,隧道断面为单洞单线马蹄形,洞径约6.2 m,掘进总长度约1077.4 m,区间左、右线间距16.5 m,隧洞拱顶至铁路路基底面的竖向距离约15.1 m.区间隧道与鹰厦铁路位置近似呈现空间下穿正交,夹角为83°,鹰厦铁路为路基—挡墙式结构,设计限速＜120 km/h,为Ⅱ型轨道,隧道与下穿铁路位置关系如图2所示.

图2 新建隧道与铁路位置关系

2.2 土层参数

结合实际工程地质勘探,新建隧道穿越主要土层物理力学参数见表5.

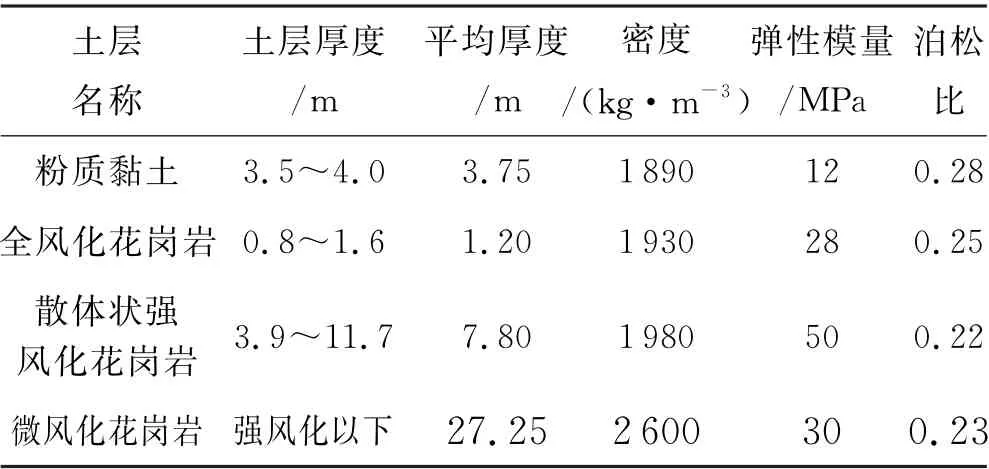
表5 岩土体物理力学参数

2.3 鹰厦铁路路基沉降最大允许值确定

3 下穿铁路结构爆破振动控制标准的数值模拟研究

3.1 建立模型

铁路结构为铁路路基形式,模型部分包含土层、隧道、道砟、铁路路基及钢轨部分.考虑边界影响模型尺寸取40 m×40 m×100 m,其中掌子面开挖方向100 m,上方铁路结构位于掌子面开挖方向45～55 m处,隧道拱顶距离铁路路基底15.1 m,隧道左右中心距16.5 m 均按实际工程情况设计.建立模型采用单元为Solid185和3DSolid164实体单元,模型网格划分单元数为1 906 564,节点数为2 026 708,最小单元网格为2 cm,模型整体示意图如图3所示.

图3 模型建立

路基、道砟及轨道结构参数主要根据实际工程地质勘测报告及部分文献[19-20]得到,见表6.钢轨本构采用各向同性线弹性模型,岩土体本构选用塑性随动硬化材料模型.

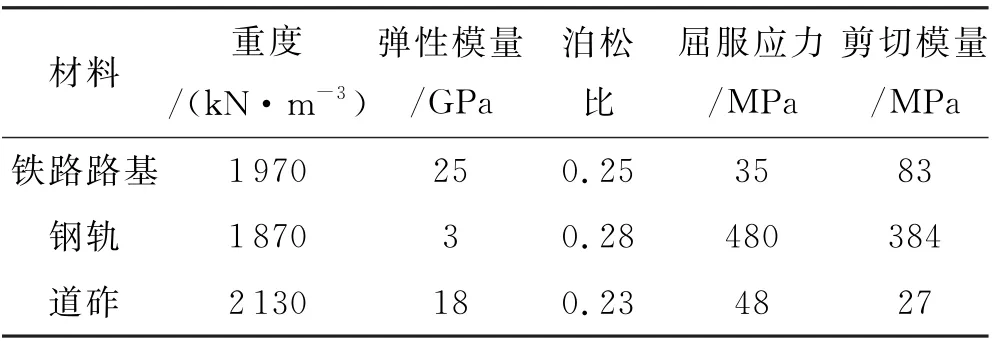
表6 模型材料物理力学参数

3.2 模型考虑重力作用影响

考虑到实际施工中存在重力作用,为确保施加爆破荷载后动力计算结果准确,模型应考虑自重作用产生的位移影响,且铁路结构线路变形应由爆破作用和自重作用共同产生,但考虑到爆破作用对铁路结构的振动变形影响是瞬态的,即爆破作用对铁路结构产生的变形影响远比自重作用产生的变形大,因此在数值分析过程中,模型应在铁路结构消除自重作用产生位移影响下进行爆破动力计算,且计算结果可以视为由爆破振动产生形变.目前有学者[18-19]采用将自重作用产生的边界节点反力施加于人工边界,通过内力平衡的方式消除自重作用产生位移,这样模型在进行爆破动力计算时基本没有自重作用产生的位移影响.

3.3 ls-dyna施加等效爆破荷载的动力计算

ls-dyna进行动力计算的关键是确定等效爆破荷载曲线、荷载大小、作用时间以及作用位置.

由于爆破开挖时[21-22],爆炸应力波均匀地作用在隧道洞周上,爆炸作用刚开始时对围岩的压应力急剧上升,达到峰值后又立刻衰减,整个爆炸过程都非常剧烈.因此选择三角形峰值荷载来简化替代实际爆破荷载模拟爆炸应力波对围岩的作用过程,荷载形式如图4所示.

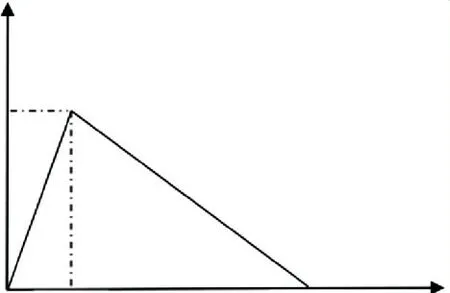
图4 三角形爆破荷载峰值

已有研究表明[21-23],将爆破峰值荷载以压力的形式均匀施加在开挖隧道的洞周,压力方向垂直向里指向隧道洞周,通过这种简化和施加爆破荷载的方式计算出的结果与直接将爆破荷载作用于炮孔壁的计算结果基本一致.爆破荷载应力峰值按式(8)确定[21-23]:

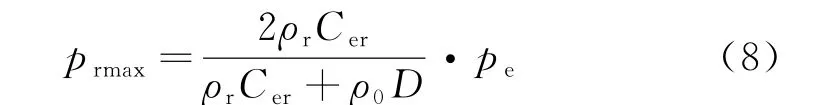
式中:prmax为岩体冲击波的初始波峰压力;ρr为岩石密度;Cer为岩体纵波波速;ρ0 为炸药密度;D为炸药爆速;pe为炸药爆轰压力,可由式(9)确定[18-19]:

根据爆破荷载的作用时间[21-23],其中加载到峰值压力的升压时间为0～10 ms,卸载时间为10～110 ms,则本次模拟中加压时间为10 ms,卸载时间取80 ms,总计算时间取200 ms.

结合工程实际围岩密度、炸药参数等将爆破理论峰值列于表7.爆破荷载峰值曲线如图5所示.

表7 爆破峰值荷载理论计算结果

图5 爆破荷载峰值曲线

3.4 爆破掘进开挖下铁路振动响应的数值分析

为动态分析隧道爆破开挖对上方铁路结构的振动响应机理,在数值分析过程中,选取爆破掘进距离为控制变量,分析铁路路基沉降变化趋势和振动响应规律,铁路结构位于爆破掘进段45～55 m 上方,爆破掘进距离0～100 m 内间隔10 m 的10组模拟计算结果见表8.

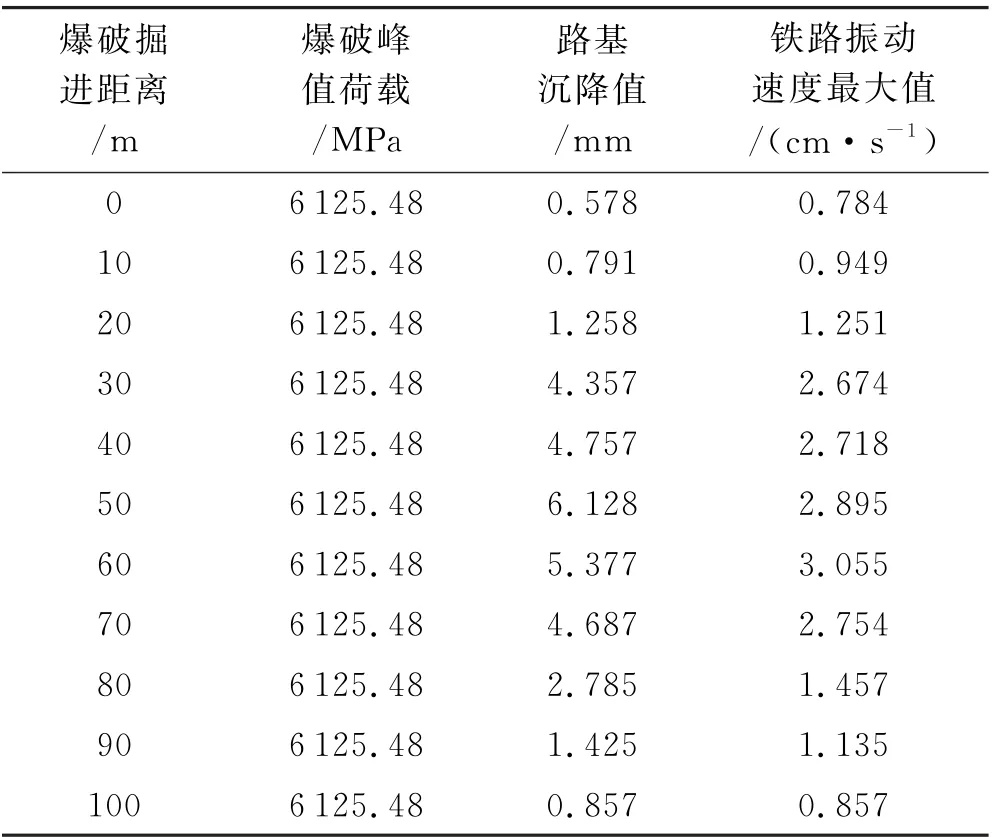
表8 爆破掘进距离变化下路基沉降模拟结果

结合图6分析,结果表明:当隧道爆破掘进段靠近上方铁路结构时,铁路路基沉降值逐渐增大,当隧道爆破掘进段进入铁路结构正下方时,路基沉降突然加剧,在铁路中心线附近路基沉降达到最大值,当爆破掘进段远离铁路结构时,路基沉降值又减小,最后趋于平缓,铁路路基的沉降变形和振动速度存在一定范围内的正相关性.

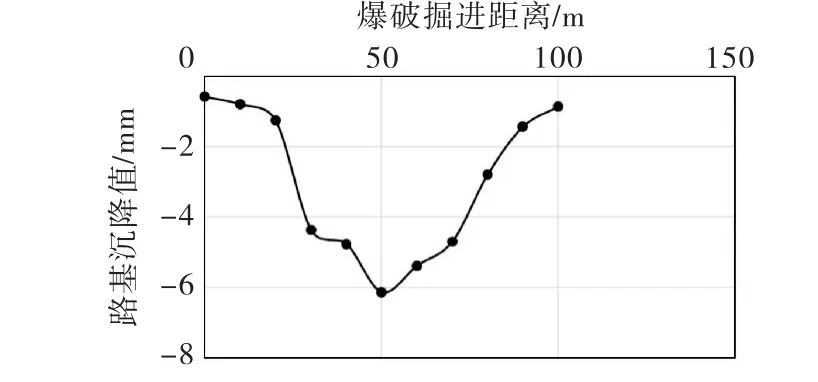
图6 不同爆破掘进距离下铁路路基沉降变化规律

3.5 基于铁路路基沉降允许值的振动控制标准数值分析

为得到合理的铁路振动控制标准以控制铁路路基的沉降允许值5 mm 为计算依据,取9次不同爆破掘进距离下的开挖工况数值计算结果分析,见表9.

表9 不同开挖工况下铁路振速计算

结合图7分析,当铁路路基沉降的控制值达到5 mm 时,铁路结构的振动速度在2.6～2.9 cm/s范围内浮动,基于施工安全考虑,取不同开挖工况下最小振速2.6 cm/s为本工程的振动控制标准.

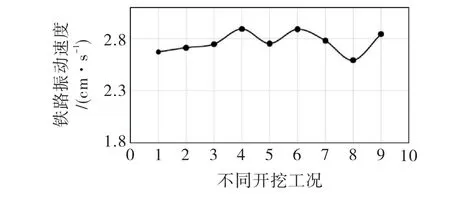
图7 路基沉降控制值为5 mm 时振速计算结果

4 结 论

1)通过Peck沉降槽理论分析路基沉降与地面沉降的关系,计算得出下穿铁路路基沉降的理论允许值为5 mm.

2)用ls-dyna计算得到爆破掘进距离与铁路路基沉降值的关系:当爆破掘进段靠近上方铁路结构时,铁路路基沉降值逐渐增大,当隧道爆破掘进段进入铁路结构正下方时,路基沉降突然加剧,在铁路中心线附近路基沉降达到最大值,当爆破掘进段远离铁路结构时,路基沉降值逐渐减小,最后趋于平缓.

3)随着爆破掘进段靠近上方铁路结构时,爆破峰值荷载值逐渐减小,爆破掘进段远离上方铁路结构时,爆破峰值荷载值又逐渐增大,在铁路结构正下方爆破掘进时,路基达到沉降允许最大值所需爆破峰值最小,但振动响应最激烈,应加强支护和监控测量.

4)以本工程隧道下穿铁路爆破施工为例.通过调整爆破掘进距离和爆破峰值荷载,控制铁路路基的沉降变形值在5 mm 左右时,振动速度范围在2.6～2.9 cm/s内,取最小值2.6 cm/s为安全的爆破振动速度,即在这个振动控制标准内进行施工,是安全合理的,能为下穿铁路爆破施工提供借鉴和参考意义.