翼型近波浪水面气动特性研究

2022-01-15胡浩德马东立杨穆清郭阳

北京航空航天大学学报 2021年12期

胡浩德，马东立，杨穆清，郭阳

（北京航空航天大学航空科学与工程学院，北京 100083）

飞行器贴近水面或者地面飞行时会获得额外的升力，这种现象被称为地面效应。地效飞行器［1］是一种专门利用地面效应提供升力供低空飞行的飞行器，主要用于水面高速运输。与船舶相比，其具有阻力小、速度快等优点；与飞行器相比，其具有升阻比高、所需推进功率小、航程大等优点［2-4］。地效飞行器贴地飞行时具有不同于常规飞行器的气动特性，为此，众多学者对地面效应展开了研究［5-8］。

地效飞行器需要贴地低空飞行，然而陆地上存在建筑物、树木、山丘等各种各样的障碍物。平坦而广阔的海洋为低空飞行的地效飞行器提供了良好的应用场景。因此，绝大多数地效飞行器用于水面运输。地面效应研究中大多将地面假设为刚性平地面，但水面是自由液面并非刚性的，而且水面上往往存在波浪，并非是完全平坦的。因此，地效飞行器在水面上空实际飞行时遇到的情况与大多数地效研究中刚性平地面的假设不相符。部分学者针对自由液面这一边界条件展开了研究。Barber［9］研究了三维机翼飞过静止水面时的水面变形，研究结果显示，水面的变形可能是由翼尖涡引起的，而不是翼下压力分布的增加，而且弗劳德数越大，水面变形越小。Liang等［10-11］应用升力线理论和面元法研究了二维翼型和三维机翼经过自由液面时的气动特性，结果显示，弗劳德数对气动特性存在显著影响，三维机翼经过水面时会使得水面产生变形，同时速度较大时可用固壁代替自由液面。Bal［12］发展了迭代边界元法来研究二维翼型，研究发现自由液面会影响翼型和机翼的气动力特性，并且三维机翼经过自由液面时会在液面上产生卡尔文波。米百刚和詹浩［13］采用数值方法分析了NACA 0012二维翼型近地效应及近水面效应的非定常运动，结果显示，地面/水面的存在剧烈地影响了翼型的动态稳定特性，且水面的自由液面效应导致了2种边界条件下动态特性的差异。

海面大多数时候并不是完全静止的，海面上总是存在波浪，波浪可能会影响地效飞行器气动力特性，因此，部分学者针对该问题展开了研究。Im和Chang［14］通过数值求解欧拉方程研究了翼型NACA 6409经过波浪地面时的气动特性，通过移动的正弦曲线模拟波浪。Qu等［15］应用可压雷诺平均Navier-Stokes方程和SA湍流模型研究了地效飞行器飞过波浪地面时的气动特性，并和平地面进行了对比，研究发现，气动力呈现周期性变化，翼型飞过波浪地面和平地面时，气动力随高度的变化规律相似，并且在大迎角下，翼型飞过波浪地面时高度降低会导致上表面气流分离。Gao等［16］研究了翼型跨声速飞过波浪地面时的气动力变化，发现了激波与波浪地面的相互作用。Lee和Tremblaydionne［17］通过试验对对称翼型经过波浪地面时的气动力特性和流场结构进行了研究；在此基础上，又进一步研究了对称翼型后缘襟翼偏转后经过波浪地面时的气动特性［18］。

上述研究都是将波浪水面简化为波浪形状的地面，再以翼型经过波浪地面来模拟翼型经过水面波浪的情况。为了更进一步地模拟翼型飞过波浪水面的情况，Zhi等［19］应用了数值波浪，从而数值模拟了翼型飞过波浪水面的情况，发现波浪有其自身的扰动速度，会与翼型下的气流产生强烈的相互作用，认为在地面小间隙的情况下不能使用波浪地面完全代替水面波浪。该研究将地效飞行器飞过波浪水面的研究向前推进了一步，但并没有对水面波浪和翼型的相互作用机理做出阐述。

截止目前，针对翼型飞过波浪水面的研究仍然非常有限。翼型飞过波浪水面时气动特性的特殊性、翼型与波浪水面的相互作用机理、不同雷诺数、不同弗劳德数、不同波浪参数、不同翼型形状、不同马赫数对翼型气动特性的影响等诸多问题均没有深入研究。

本文采用数值方法对翼型小间隙经过波浪水面的气动特性做了分析，对翼型与波浪之间的相互作用机理做了深入的分析。

1 数值方法与计算验证

本文选取NACA 4412翼型。翼型弦长0.5 m，迎角为4°，来流速度范围为30～100 m/s，相应的雷诺数范围为1.0×106～3.4×106，弗劳德数范围为13.5～45.2。雷诺数Re和弗劳德数Fr的定义为

式中：V为来流速度；c为翼型弦长；g为重力加速度；ρair为空气密度；μair为空气动力黏度。

计算域和网格划分分别如图1和图2所示。网格在翼型周围和水面附近进行了加密，图2中给出了翼型和水面附近的局部放大图。翼型后缘点与水面之间的距离为h/c＝0.1。计算域的入口，上下边界距离翼型20c，出口距离翼型25c。入口边界设置为速度入口，下边界设置为无滑移壁面，上边界和出口处设置为压力出口。波浪从入口处产生向右传播。波长λ取5c，波幅a取0.05c。波浪采用了边界造波方法，在入口边界处定义气相和液相的速度及波面表达式，水面通过流体体积函数方法（VOF）捕捉，波浪是基于一阶线性波理论［19］的线性微幅波。湍流模型采用k-ω模型。对水面处的网格进行了加密，波长和波高方向上的网格尺寸分别为1/（8a）和1/（25a）。时间离散为二阶隐式格式，空间离散为二阶迎风格式。考虑到非定常计算的稳定性与计算精度，时间步长Δt的选取需满足：

图1 计算域Fig.1 Computing domain

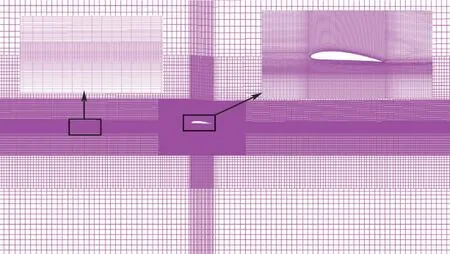
图2 网格划分Fig.2 Grid generation

式中：Δx为网格最小尺寸。

网格通过ANSYS ICEM 软件划分，使用Star CCM+软件进行数值计算。收敛判断标准为数值计算残差和气动力系数的周期性变化，计算残差小于1×10-6，同时气动力系数开始周期性变化，则判定数值计算收敛。

在进行CFD计算之前先对其准确性进行验证。许多学者［4，7，9，20］采用了数值计算和试验等多种方法对NACA 4412翼型进行了大量的研究。试验数据取文献［21］中的试验数据。迎角取4°，地面间隙为h/c＝0.15，雷诺数为3.0×105，这些条件均与文献［21］中的试验条件一致。翼型表面压力系数Cp沿翼型弦向分布计算结果如图3所示，x为翼型表面点与翼型前缘点的水平距离，c为翼型弦长，x／c即为翼型表面点与翼型前缘点的相对距离。由图3可见，计算结果与试验结果吻合得很好。同时，还对网格无关性进行了验证，表1为不同网格数量下的计算结果对比，网格选取中等网格数量即可满足精度需求。Y+为边界层网格与壁面的无量纲化距离。

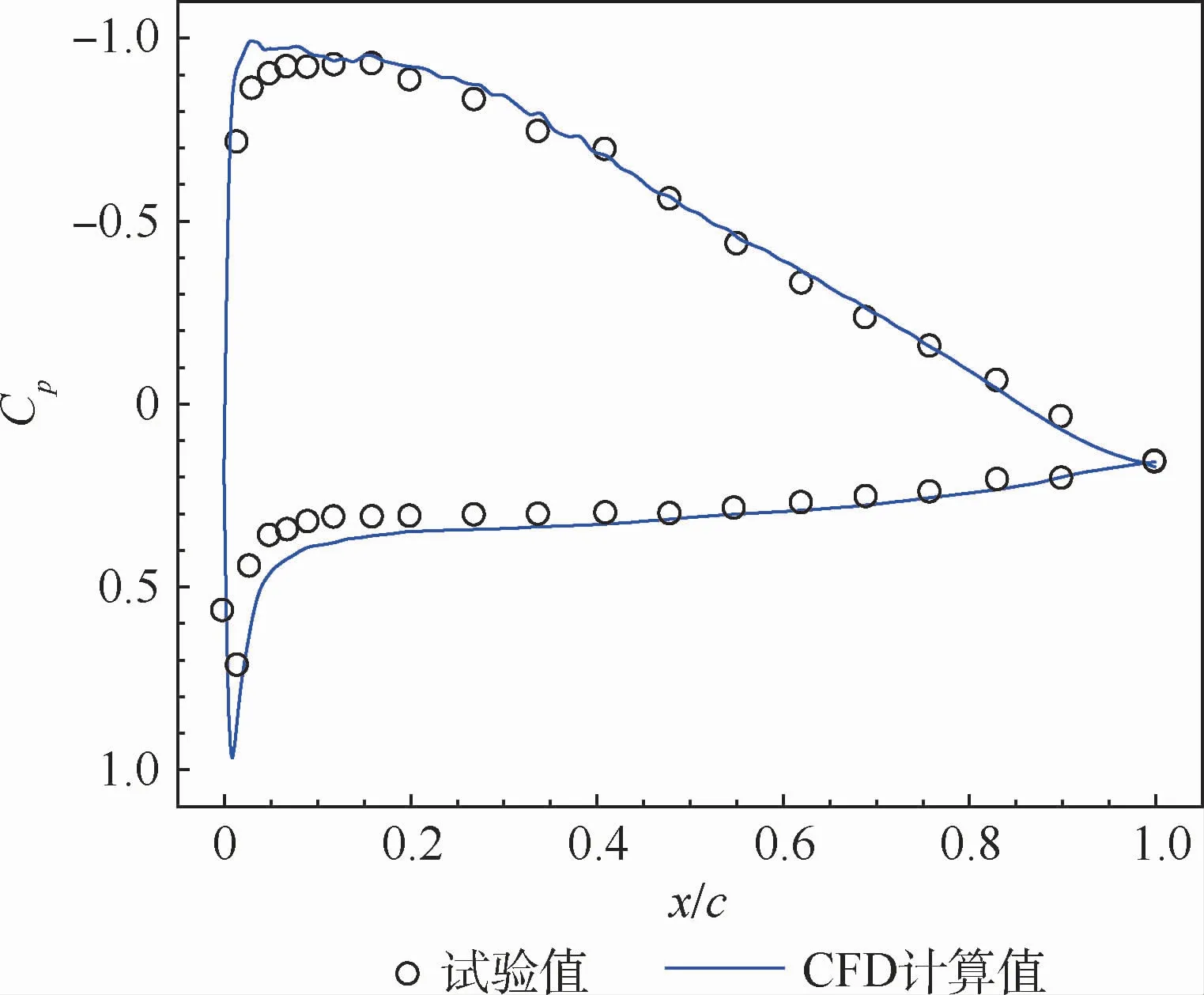
图3 压力系数的计算值和试验值对比Fig.3 Comparison of computed and experimental pressure coefficient

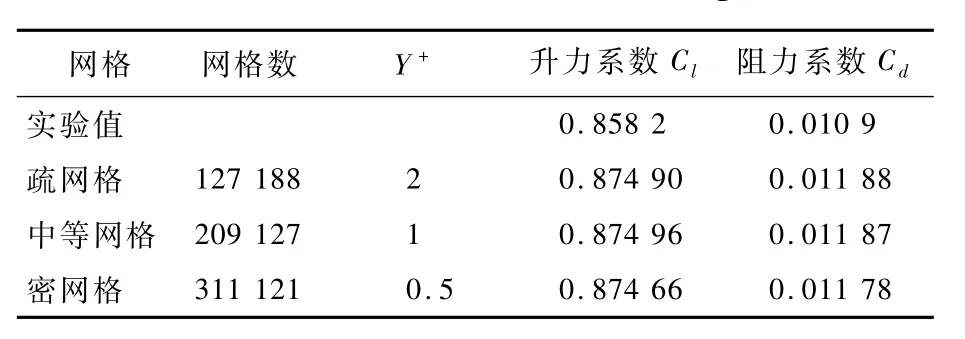
表1 实验值与不同网格数量下的计算结果Table 1 Calculation results with different grid numbers

波浪的数值模拟常常存在衰减等问题，因此，在计算前对波浪的波面形状进行验证。本文原点设置在翼型前缘处，因此在原点前1个波长处、原点处及原点后2个波长处3个地方设置了波高监测点，各个监测点处的波形随时间的变化与理论波形的对比如图4所示。图中纵轴Z表示波高监测点处的波高，t为翼型和波浪的相对运动时间，初始时刻即为t＝0。

图4 波形计算结果与理论结果对比Fig.4 Comparison of calculated and theoretical results of waveform

由图4可见，数值计算结果与理论结果相比，波谷处的衰减比波峰处的稍大，同时x＝2λ处相比x＝0和x＝-λ处的波峰衰减更明显。总体而言，波形计算结果与理论波形很接近，表明数值方法能够很好地模拟波浪。

2 计算结果与分析

2.1 气动特性

以翼型后缘点为参考点，初始时刻翼型后缘点在波峰正上方。T为1个波浪周期，翼型在1个周期内相对波浪的运动距离为1个波长。定义t*＝t／T来描述翼型与波浪之间的相对位置。当t*＝0和t*＝1时，翼型后缘点均位于波峰正上方，因此，这2个时刻是等价的。对于波浪水面的情况，非定常计算模拟了20个周期以上；对于固壁波浪的情况，由于网格滑移距离的限制，首先在网格无滑移的条件下计算收敛，在此基础上网格滑移运动，计算了10个周期以上，结果达到前文所述收敛标准。2种边界条件下的计算结果均取自最后2个周期。

翼型经过波浪水面和固壁波浪地面时，升力系数Cl、阻力系数Cd及力矩系数Cm在2个周期内的变化如图5所示。其中固壁波浪的波高、波长等波浪参数设置均与水面波浪一致，采用滑移网格计算，计算域的设置与文献［16］相似，网格密度与计算波浪水面时的设置一致。图中给出了不同来流速度下的气动力系数，不同来流速度对应的雷诺数和弗劳德数如表2所示。

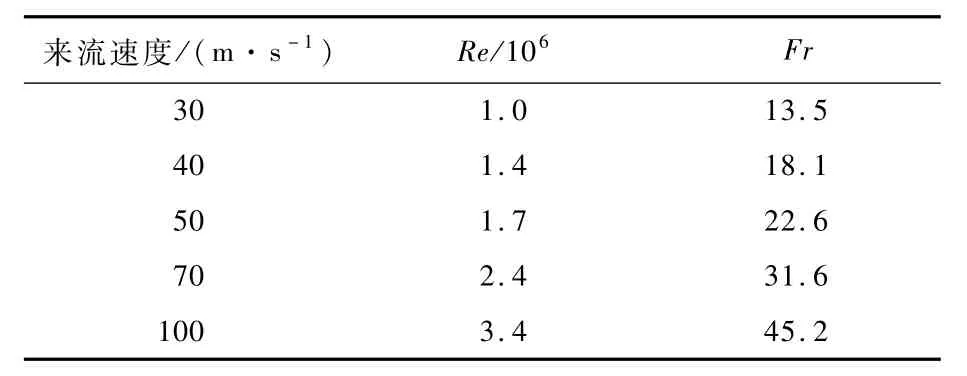
表2 不同来流速度对应的雷诺数和弗劳德数Table 2 Re and Fr corresponding to different velocities

图5 不同来流速度下2个周期内气动力系数变化Fig.5 Variation of aerodynamic coefficient in two cycles at different velocities

固壁波浪地面条件下的升力系数、阻力系数及力矩系数曲线均近似正弦变化，同时可以看到，不同来流速度下的气动力系数变化趋势相同，不同的只是数值大小，来流速度的改变仅会引起气动力系数向上或者向下平移。

对比翼型经过水面波浪和固壁波浪气动力变化可以看到二者之间的差异显著。首先，气动力系数曲线形状存在明显差异，经过固壁波浪时，气动力系数在1个周期内的变化曲线近似正弦曲线，而经过波浪水面时气动力系数的变化曲线并不是正弦曲线。其次，来流速度的改变对气动力系数的影响差异显著，翼型经过固壁波浪时，来流速度的改变不会影响气动力系数曲线的形状，仅仅会使得曲线向上或者向下移动。而翼型经过波浪水面时，来流速度的改变对气动力系数曲线形状会有所改变，而且来流速度的改变并不会使得气动力系数曲线向上或者向下移动，改变的是气动力系数的波动范围。再者，气动力系数的变化范围也存在明显差异，可见不论是时均值还是波动性，2种地面条件下均差异显著。因此，在翼型距离地面较近飞行时，不能用固壁波浪地面代替水面波浪。

为了更方便地研究翼型气动特性，将翼型通过前缘点和后缘点分割为上下表面，上下表面的升力系数分别定义为Cl，up和Cl，down，上下表面的阻力系数分别定义为Cd，up和Cd，down，上下表面的力矩系数分别定义为Cm，up和Cm，down。取来流速度30 m/s时翼型经过波浪水面和固壁波浪的情况。气动力系数在1个时间周期内的变化如图6所示。

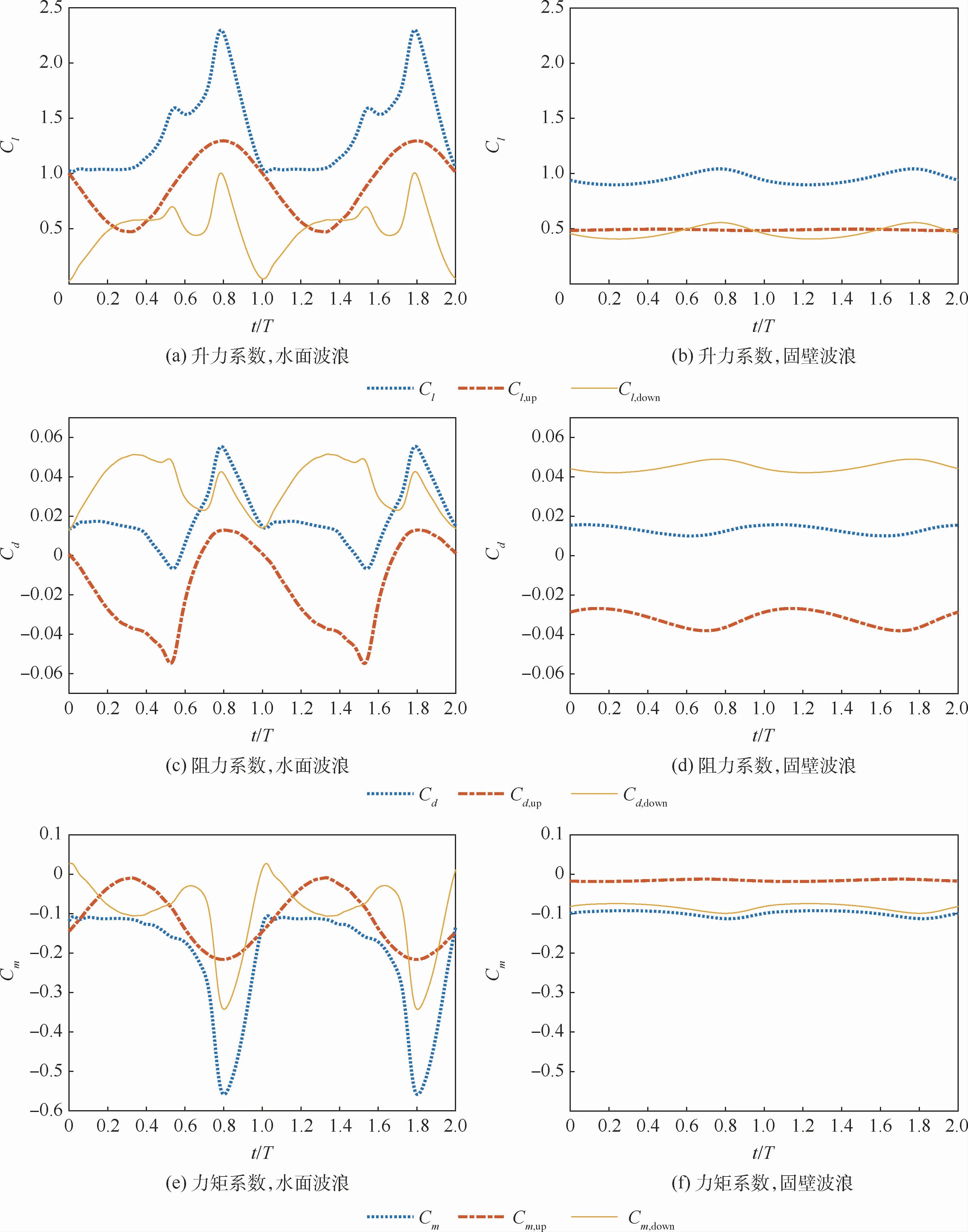
图6 气动力系数随时间的变化曲线Fig.6 Variation of aerodynamic coefficient with time

由图6可见，翼型经过波浪水面时，对于升力系数而言，上表面的升力系数变化近似正弦曲线的周期变化，而下表面的变化曲线并不规则，导致总升力系数呈现出了和下表面升力系数相似的变化趋势。力矩系数和升力系数相似，上表面的力矩系数变化近似正弦曲线，下表面的力矩系数并未呈现出类似正弦曲线的变化。阻力系数不同于升力系数和力矩系数，上表面的阻力系数变化曲线和正弦曲线略有差异，其谷底较尖锐，而下表面的阻力系数变化曲线和正弦曲线存在明显差异。翼型上下表面的升力系数和力矩系数的变化表明，翼型经过波浪水面时，波浪的存在更多的是影响翼型下表面气动力的变化。

翼型经过固壁波浪时，对于升力系数而言，上表面的升力系数波动幅度很小，而下表面的波动幅度较大，因此，升力系数的周期性变化主要是下表面造成的。力矩系数和升力系数的变化相似，上表面力矩系数波动很小，而下表面的波动幅度较大，因此，力矩系数的周期性变化主要是下表面造成的。阻力系数上下表面波动幅度相差不大，上表面阻力系数为负主要是翼型前缘吸力峰造成的，上下表面的波动方向相反，下表面阻力系数增大时上表面的阻力系数在减小，下表面阻力系数减小时上表面的阻力系数在增大，从而造成了总阻力系数波动比上下表面的都小。

2.2 流场分析

翼型经过水面波浪和固壁波浪时，不同时刻的速度云图如图7所示，V*为当地速度与来流速度的比值。在左侧图片中较粗的实线为水面。

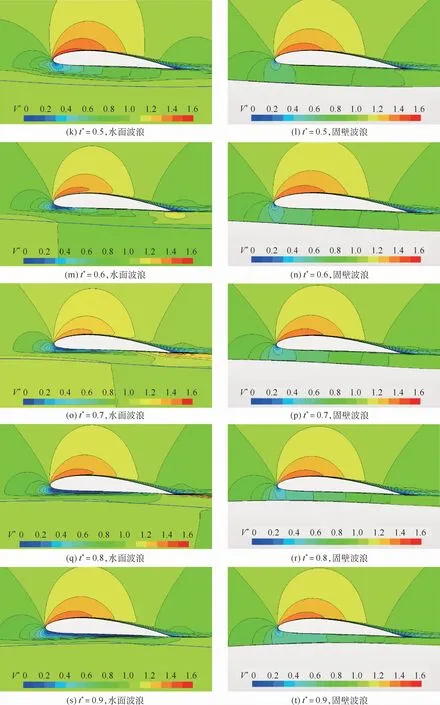
图7 不同时刻下翼型周围速度云图Fig.7 Velocity contours around airfoil at different moments

翼型经过水面波浪时的速度云图和经过固壁波浪时的速度云图存在显著差异。当翼型经过固壁波浪时，翼型下方气流速度变化可以通过流管的收缩或者扩张来解释，这和现有的研究发现是相同的，而翼型经过波浪水面时，下方气流速度变化呈现出了较为复杂的现象，难以简单地用水面和翼型下表面形成的气流通道来解释。

在水面处设置速度监视器监视水面上水质点的速度变化，在t*＝0时刻的水面质点水平速度Vu和垂直速度Vw如图8所示，取距离翼型前缘点上下游7个弦长处的速度分布。图8中也给出了在相同时刻固壁波浪表面上的质点运动速度，用点划线表示。虚线之间是翼型所在的位置。由图可见，水面上的质点在垂直方向上存在速度分量，而且该速度分量呈波动变化，在水平方向上的速度分量使得来流速度大小也呈现出了波动变化。相应的固壁波浪表面质点在垂直方向上的速度分量为0，水平方向上的速度分量等于来流速度。这是因为对于固壁波浪而言，波浪壁面上的所有质点均做水平直线运动，而水面波浪的水面处质点不光存在水平向右的速度，还存在垂直向上的速度分量，而且随着时间的变化而波动变化，这是水面波浪与固壁波浪的显著不同之处。

从图8中还可以看到，翼型正下方水面质点速度不同于翼型前方一个波长处的速度，表明翼型的存在使得波浪表面质点运动速度受到了影响，由此表明，翼型和水面波浪之间存在相互作用。

图8 水面质点在水平和垂直方向上的运动速度Fig.8 Horizontal and vertical velocity of particles on water surface

接下来对翼型经过水面波浪时的流动机理进行分析。翼型的压力系数定义如下：

式中：p为当地静压；p∞为远前方静压；ρair为空气密度；V∞为远前方来流速度。

将翼型经过波浪水面时的时间周期分为10个时间点，在每个时间点翼型表面的压力系数如图9所示。t*＝0和t*＝1时刻是等价的。由图9可见，在t*＝0时刻，在翼型后缘下表面存在一个压力峰，t*＝0.1时刻该压力峰消失。从t*＝0～0.3时刻，翼型上下表面的压力系数均在不断地增大，即下表面的压力在不断增大，而上表面的吸力在减小，且变化幅度差不多，这解释了在t*＝0～0.3这段时间内，升力系数基本不变化这个现象。在t*＝0.4时，下表面的压力系数和t*＝0.3时基本相同，而上表面的压力系数开始减小，即上表面的吸力开始增大，从而导致升力系数开始增大。在t*＝0.4～0.8时，上表面的压力系数在持续减小，直到t*＝0.9时刻，上表面的压力系数开始增大。

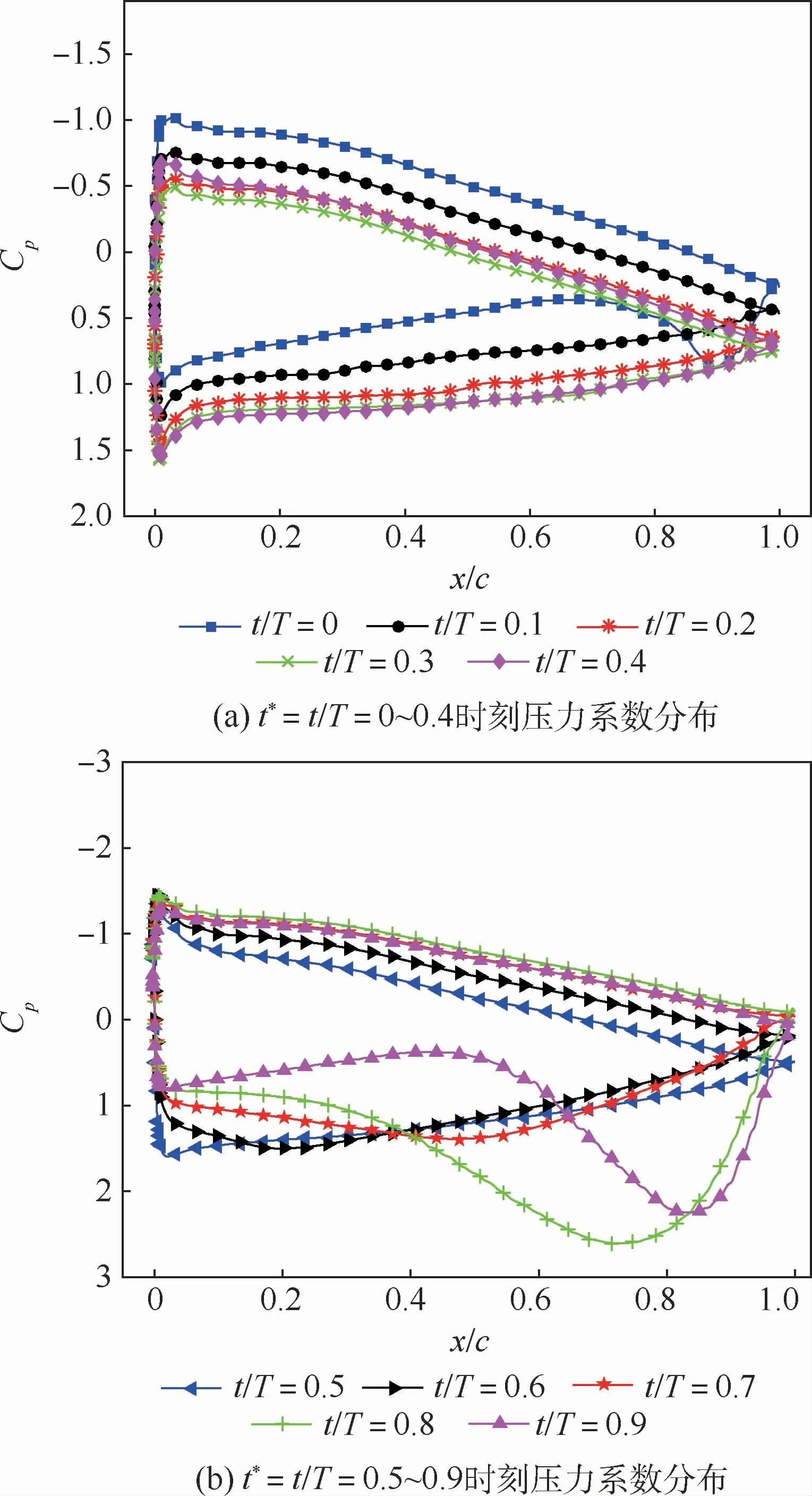
图9 不同时刻翼型表面压力系数分布Fig.9 Pressure coefficient distribution on airfoil at different moments

下表面的压力系数从t*＝0.6时刻开始发生明显的变化，在t*＝0～0.5时刻翼型下表面压力峰均发生在翼型前缘，而t*＝0.6时刻开始，压力峰开始向后移动，t*＝0.6～1.0时刻，压力峰从翼型前缘附近移动到了翼型后缘。在压力峰向后移动的过程中，压力峰值也发生了变化，在t*＝0.8和t*＝0.9时刻的压力峰值显著大于其他时刻的压力峰值。压力峰向后移动的过程中还伴随着翼型前缘附近压力系数的减小。t*＝0.8时刻下表面压力峰值达到最大，此时翼型升力系数达到最大值，阻力系数达到最大值，力矩系数达到最小值。升力系数达到最大值是因为上表面吸力达到最大值，同时，下表面的压力也达到了最大值。下表面压力峰值达到最大值使得翼型的压差阻力达到了最大值。该压力峰值靠近翼型后缘，使得翼型的低头力矩达到了最大值，即力矩系数达到了最小值。t*＝0.9时刻开始，上表面压力系数开始增大，即吸力开始减小，下表面的压力峰值也开始减小。

由压力系数还可以看到，上下表面的压力系数变化存在显著不同，上表面的压力系数变化是沿弦长方向一致增大或者减小的，下表面的压力系数在t*＝0.1～0.5时刻一致变化，在t*＝0.6～1.0时刻下表面的压力系数曲线形状发生了显著变化。这也解释了翼型上表面的气动力系数近似正弦曲线变化，而下表面的气动力系数并未呈现出此现象。

由图6可知，在t*＝0～0.3时刻，翼型下表面的压力系数是增大的，对比图9中t*＝0和t*＝0.1时下表面的压力系数可见，除翼型后缘部分以外，t*＝0.1时刻的压力系数大于t*＝0时刻的压力系数。由速度云图可见（见图7），t*＝0时刻，翼型中部下方区域的低速区域比t*＝0.1时刻的大，而压力系数却小，这不符合文丘里流管理论中的速度降低会导致压力升高的结论。结合图9中t*＝0时刻翼型下表面后缘压力峰，可推断是该压力峰导致了翼型下表面附近的回流，从而损失了压力形成了低压区。该时刻翼型下表面附近的速度矢量图如图10所示，可以清晰地看到在低速区存在回流。

图10 t* ＝0.8时刻翼型周围速度矢量图Fig.10 Velocity vector around airfoil at t* ＝0.8

由翼型下表面的压力系数可见，t*＝0.1～0.5时间段内，压力峰均发生在翼型前缘，相应的速度云图上可以看到速度滞止点也在翼型前缘附近，同时，翼型下方的气流也存在逐步加速的现象。速度云图和翼型经过固壁波浪时的速度云图相似度很高，在翼型下方也存在收敛的流管，不过流管并不是翼型下表面和水面形成的通道，以t*＝0.3为例，流管的大致轮廓如图11所示。这是因为水面上的质点存在运动速度，水面附近的空气也会随着水面的运动而运动，造成了翼型下表面实际的流管小于翼型下表面和水面构成的通道。t*＝0.1～0.3时间段，翼型经过固壁波浪时流管扩张，气流加速，压力减小，导致翼型下表面升力系数减小。而相同的时间段内，翼型经过水面波浪时下表面的升力系数在增大。因此，仅仅通过流管的扩张无法解释这段时间内翼型下表面压力系数增大的现象。

图11 t* ＝0.3时刻流管轮廓Fig.11 Outline of flow tube at t* ＝0.3

前文已分析得到翼型通过水面波浪与固壁波浪的情况不同是由于水面波浪上的质点还存在垂直运动，而且水平方向上的速度也存在一个小波动，不过该波动值相对来流速度是一个小量。因此，水面波浪表面的垂直运动是导致其流场结构特殊性的重要原因。翼型下方的水面上质点垂直方向运动速度Vw如图12所示。由图可见，从t*＝0.1到t*＝0.5，翼型下方靠近翼型前缘的水面质点速度在逐渐增大。虽然这段时间内翼型与水面之间的距离在扩大，但是翼型下方靠近翼型前缘的水面质点垂直运动速度的增大抵消了流管的扩张效应，从而使得下表面压力增大。

图12 翼型下方水面质点垂直方向运动速度Fig.12 Vertical velocity of particles on water surface below airfoil

在t*＝0.6～1.0时间段，翼型下表面的压力峰从前缘向后移动，压力峰意味着翼型下方存在高压区，高压区阻碍了气流的流动，导致了回流区的产生，回流区内压力损失。从图9可以清晰看到，翼型下表面前缘至压力峰这段回流区内压力系数的减小。翼型下表面回流区的存在及在该时间段内翼型与水面的距离越来越近，导致更多的气流从翼型上表面流过，上表面的流速增大，吸力也增大。上表面吸力的增大及下表面压力峰的增大超过了下表面回流区的存在导致的压力减小，因此在t*＝0.6～0.8这段时间内，翼型升力系数在增大。而下表面的升力系数在这段时间内先减小后增大，这是因为在t*＝0.6～0.7时间段压力峰在后移的过程中并没有增大，回流区扩大导致的压力系数减小主导了下表面升力系数的变化。在t*＝0.7～0.8时间段，回流区内压力系数减小幅度较小，而压力峰显著增大，导致下表面升力系数增大。在t*＝0.8～1.0时间段，上表面的升力系数开始减小，在t*＝0.8时翼型前缘到达了水面波浪的波峰，此后在t*＝0.8～1.0时间段翼型前缘与水面的距离逐渐增大，同时下表面压力峰值也在减小，二者的综合作用导致了流过上表面的气流减小，上表面气流减速，吸力降低，上表面的升力系数减小。下表面回流区的扩大导致了更大程度的压力降低，压力峰也在减小，二者的综合作用导致了下表面升力系数的降低。上下表面升力系数的同时减小导致了翼型升力系数急剧减小。

t*＝0.6～0.9时间段内翼型下表面存在明显的回流区，结合翼型表面压力系数分布图9和翼型下方水面质点速度图12可见，翼型下表面压力峰值的位置和翼型下方水面质点速度存在对应关系。t*＝0.6时刻，翼型前缘下方水面质点速度曲线呈现出向右上方隆起的现象，相应地，速度云图呈现出了前缘附近的流管受到压缩的现象。t*＝0.7时刻，翼型下方水面质点运动速度峰值发生在翼型中部，此时，翼型下表面压力峰也出现在翼型中部。t*＝0.8～1.0时刻，翼型下方水面质点运动速度峰值向后移动，相应地，下表面压力峰也向后移动，可见翼型下方水面质点速度是引起下表面压力峰变化的主要原因。在t*＝0.7～1.0时间段，翼型下方水面质点运动速度在翼型弦长方向上的分布曲线存在峰值，且该峰值大于零，即水面质点在向上运动，在向上运动的过程中挤压翼型与水面之间的空气，从而使得翼型下表面的压力骤增，产生了压力系数大于1的压力峰值。

对于单相不可压缩流动，翼型表面的最大压力出现在前缘停滞点。驻点压力是气流的静压和动压之和。根据压力系数的定义，单相不可压流压力系数的最大值为1。然而，当翼型在波浪形水面上移动时，最大压力系数超过了1。这证明了水面上的质点向上运动会挤压机翼下方的空气。t*＝0.8时刻翼型周围的压力云图如图13所示，可以明显看到翼型与水面之间的高压区。

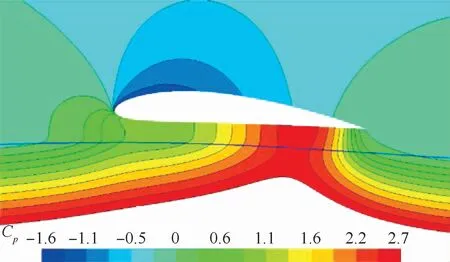
图13 t* ＝0.8时刻翼型周围的压力云图Fig.13 Pressure contour around airfoil at t* ＝0.8

在解释了波浪与翼型之间的相互作用机理后，可以解释气动系数随流速的增加而减小的现象。水面质点的垂直速度决定了翼型下方空气的压缩程度，从而决定了翼型气动力的变化。气动力系数的变化定义为

式中：ΔC为气动力系数的变化；ΔF为气动力的变化。

在波浪的波长和波幅不变的情况下，来流速度的增加对水面质点的垂直速度没有影响，因此，气动力ΔF不变。但气动力系数ΔC的变化与来流速度平方成反比。因此，来流速度越大，气动系数的波动幅度越小。对于100 m/s的来流速度，固壁波浪和水面波浪的空气动力系数曲线对比如图14所示。由图可知，水面波浪的气动系数在1个周期内的变化与固壁波浪相似。