无人集群系统行为决策学习奖励机制

张婷婷，蓝羽石，宋爱国

（1.陆军工程大学指挥控制工程学院，南京 210017； 2.中国电子科技集团公司第二十八研究所，南京 210017；3.东南大学仪器科学与工程学院，南京 210096）

无人集群系统是近年来国内外军事领域发展的重要作战系统，推动无人作战样式由“单平台遥控作战”向“智能集群作战”发展［1］。例如，无人机集群作战是无人集群系统典型的作战样式。无人集群系统可以看作是由若干同构或者异构的无人装备通过自组织构成的智能群体，形成分布式感知、目标识别、自主决策及协同规划与攻击能力，具有交互学习和智能涌现的群体智能特征［2］。人类期望无人集群有自学习、自决策的自主作战能力，随着人工智能技术的发展，无人系统行为自主决策成为可能［3］。无人集群系统往往面临对抗任务，在此类情况下，实现各个无人执行模块高效准确地协同完成既定任务，亟须研究构建在对抗环境中无人系统协同完成任务的高效行为决策方法，如何提高自主行为决策效率是关键问题。目前，勘测、侦察及公共安全等领域所采用的大多既定环境和任务规划下的协同操作策略，缺乏对抗任务下多无人系统自适应感知与自主协同的行为生成策略。在双方对抗任务中，从单个无人系统视角看，其他协同无人系统也是动态变化的，行为是未知的，导致执行环境动态性增强，增加无人系统适应动态环境的不确定性和行为自主决策学习的复杂度，改变传统单智能体学习所依赖的环境转移的不确定性，导致智能体学习的复杂度。

目前，多智能体深度强化学习用于无人集群系统自主行为策略学习是主流的方法。无人系统通过试探和奖励反馈形成决策行为。在设计时，通常会精心设计信息丰富的奖励功能，以引导无人系统正确的行为策略。对于许多实际问题来说，定义一个好的奖励函数并非易事。例如，只在无人系统成功完成任务时奖励，为了完成这个任务需要长时间的试探行动过程，那么奖励就变得很少，在疏松奖励情况下，无人系统策略学习效率非常低。本文增加动作空间边界碰撞惩罚、智能体间时空距离约束满足程度奖励；同时通过智能体在群体中的关系特性，增加智能体间经验共享，进一步优化学习效率。在实验中将先验增强的奖励机制和经验共享应用到多智能体深度确定性策略梯度（Multi-Agent Deep Deterministic Policy Gradient，MADDPG）算法中，多智能体行为学习效率显著提升。

1 相关工作

2017年，谷歌的DeepMind团队开创性地提出MADDPG算法［4］，实现多智能体在协同与对抗的复杂场景中的自主行为决策学习，该算法考虑到智能体之间的协同与对抗关系，设计协同与对抗关系奖励函数。另外，该算法对所有智能体策略进行估计，训练时充分利用全局信息，执行时策略只用局部信息，以缓解执行环境不稳定问题。利用该算法可以解决连续动作空间的无人集群自主对抗策略生成问题。

MADDPG算法虽然解决了多Agent环境的不稳定问题，但解优化性能不好。深度强化学习中最大的难点是对领域问题求解时奖励函数的设计，扩展至多智能体场景时，这一问题更加显著，直接决定了智能体是否能学到目标策略，并影响算法的收敛性和最终的实现效果。近年来，诸多学者围绕该问题进行了研究。文献［5］提出了一种带有网络参数共享机制的MADDPG算法，在此基础上，针对多智能体合作场景中奖励函数设计难题，提出了一种基于群体目标状态的奖励函数，并进一步把带优先级的经验重放方法引入多智能体领域，训练出了稳定的协同策略。文献［6］提出了一种基于赫布迹和行动者-评价者框架的多智能体强化学习方法，利用赫布迹加强游动策略的学习记忆能力，基于同构思想实现了多智能体的分布式学习。文献［7］提出了一种改进的多目标追踪方法，基于追踪智能体和目标智能体数量及其环境信息建立任务分配模型，运用匈牙利算法根据距离效益矩阵对其进行求解，得到多个追踪智能体的任务分配情况，并以缩短目标智能体的追踪路径为优化目标进行任务分工，同时利用多智能体协同强化学习算法使多个智能体在相同环境中不断重复执行探索—积累—学习—决策过程，最终根据经验数据更新策略完成多目标追踪任务。文献［8］提出一种基于MADDPG的改进算法——GAED-MADDPG，解决了多智能体强化学习算法收敛时间过长和可能无法收敛的问题。文献［9］提出了基于并行优先经验回放机制的MADDPG算法（PPER-MADDPG），采用并行方法完成经验回放池数据采样，并在采样过程中引入优先回放机制，实现经验数据并行流动，数据处理模型并行工作，经验数据优先回放，提升了MADDPG算法性能。文献［10］在基于MADDPG算法的基础上，设计了一种CGF空战策略生成算法，为了提高空战策略生成算法的效率，提出了一种基于潜力的奖励形成方法，得到的策略具有较好的收敛性和较好的空战性能。文献［11］提出了一种基于经典MDRL算法的MADDPG并行评价方法（MADDPG-PC），引入了一种策略平滑技术来减小学习策略的方差，提高了多智能体协同竞争环境下训练的稳定性和性能。文献［12］针对MADDPG算法学习效率低、收敛速度慢的问题，研究了一种优先体验重放（PER）机制，提出了一种优先体验重放MADDPG（PER-MADDPG）算法，基于时间差（TD）误差，设计了优先级评估功能，以确定从回放缓冲区中优先采样的体验，解决了智能体学习效率低、算法收敛速度慢的问题。

通过实验发现，仅采用现有的MADDPG算法用于无人集群系统协同对抗行为策略生成，奖励为稀疏奖励，在训练过程中，奖励信号变化不明显，导致智能体采用策略梯度算法进行探索时成功样本数量少，需要长时间训练才能达到最优策略，算法的收敛性表现较差，从而很难真正意义上实现对抗任务下无人集群系统自主行为快速学习，需要提高算法收敛效率。

本文改进MADDPG算法的奖励机制，提出Per-Distance奖励机制。①引入动作空间边界的惩罚、智能体时空距离惩罚，解决延迟奖励问题，以提高无人集群系统行为学习效率；②通过智能体在群体中的关系特性，增加智能体间经验共享，提高无人集群系统合作学习效率。通过实验验证该方法提高了行为学习收敛速度，使其更加稳定。从而提高对抗任务下无人集群行为决策学习的效率。

2 问题描述

针对无人集群系统用多智能体强化学习算法解决行为策略学习，存在奖励稀松、学习效率低下的问题，本文采用MADDPG算法为学习算法，重新设计奖励函数，用于红方无人机群协同围捕蓝方无人机任务案例中，以无人机为智能体实体，验证无人机群协同自主围捕行为效率。

2.1 无人机运动学模型

无人机集群协同围捕是集群作战的典型样式，作战空域内存在多个捕食者和逃逸者，两方无人机具有相反的战术目的，捕食者要追击捕食逃逸者，而逃逸者要躲避远离捕食者追踪。多无人机的捕食-逃逸场景如图1所示。

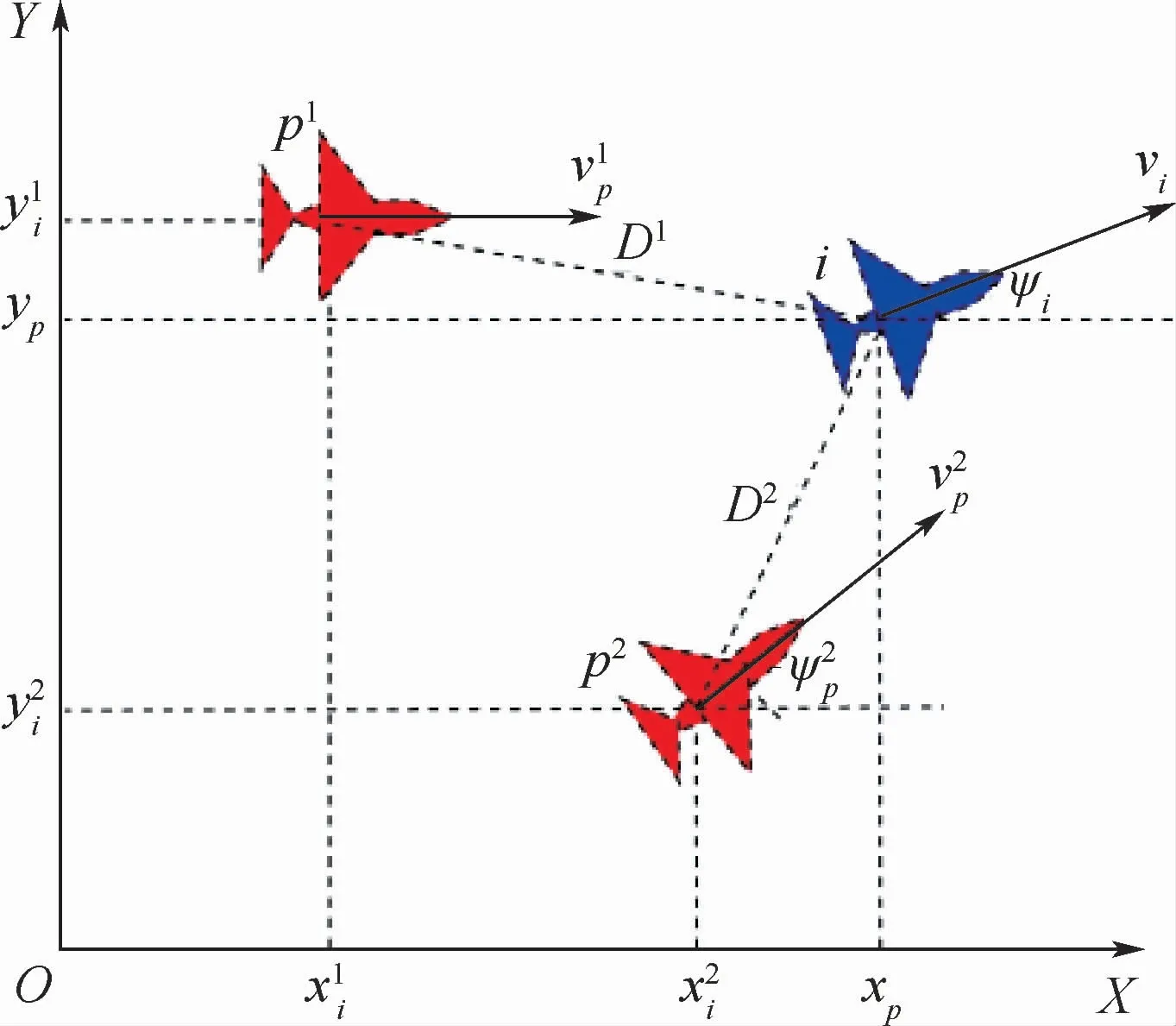
图1 捕食-逃逸几何模型Fig.1 Geometric predation-escape model

本文假定捕食-逃逸问题在有限的二维平面内进行，图1为二维平面区域的捕食-逃逸对抗的笛卡儿直角坐标系，捕食者i和逃逸者p的速度分别为vi、vp，速度航向角分别为ψi、ψp。捕食者无人机的运动学方程为

捕食者和逃逸者的运动需满足边界约束：

式中：xmin、ymin分别为环境边界的最小横纵坐标；xmax、ymax分别为环境边界的最大横纵坐标。当捕食者和逃逸者触碰到边界速度降为零。

2.2 MADDPG算法

2.2.1 算法核心思想

在多智能体强化学习训练过程中，每个智能体的动作是实时变换的，从单智能体视角观测到的环境是不断变化的，从而造成学习算法收敛性差是多智能体深度强化学习当下的困境。为解决该问题，MADDPG算法引入中心化训练、分布式执行的方法，采用Actor-Critic（动作-评价）网络更新策略，以解决训练不稳定性问题。具体方法是：在智能体训练时，将其他智能体的动作信息Actor加入到环境状态中，在t时刻，添加所有智能体的执行动作，作为下一个时刻t＇的环境状态，加入可以观察全局的Critic网络来指导Actor网络训练。测试时只使用有局部观测的Actor采取行动，将不稳定的环境状态变为稳定的环境状态，降低多智能体行为决策的复杂度。

2.2.2 基本假设

MADDPG算法遵循马尔可夫决策过程［13］，可以定义为一个多元组〈S，A1，A2，…，An，R1，R2，…，Rn，T，O，γ〉。智能体所处的环境中包含了n个智能体，S为环境的状态空间。Ai（i＝1，…，n）表示单个智能体i的动作空间，而A1×A2×… ×An表示所有智能体的联合动作空间。Ri由一系列的ri求和而成，表示智能体i的奖励总额，ri为多智能体执行联合动作A时，从状态s∈S转移到状态s′∈S时智能体i所获得的即时奖励。T：S×A×S→［0，1］为状态转移函数，表示多智能体在状态S下，执行联合动作A后转移到状态S′的概率分布。oi∈O为智能体i对环境的观测值，观测属性又可以分为部分观测和完全观测。γ为折扣因子，用于调节长期奖励与即时奖励之间的权重。在多智能环境中，状态转移是所有智能体共同行动的结果。n个智能体根据自身的观测值oi及所获得的即时奖励ri做出行为决策ai，共同输出联合动作A促使环境状态S发生转移。因此，智能体的奖励与联合策略有关。所有智能体的参数集合为θ＝｛θ1，θ2，…，θn｝。假设智能体每次采用的确定性策略为μ，每一步的动作都可以通过公式at＝μ（St）获得，而执行某一策略后获得的奖励，奖励值大小由Q函数决定，实现确定通信方式下多智能体的竞争、合作博弈。

算法运行条件为：①学习策略基于单Agent视角观测信息；②Agent自身的行为仅仅取决于策略；③Agent之间的通信为全联通模式。

2.2.3 算法执行

算法执行过程如图2所示。区别于共享环境下Agent视角，每个Agent的输入状态不一样，每个执行者与环境交互，无需关注其他Agent状态，环境输出下一个全信息状态Sall后，执行者Actor1和Actor2只能获取自己能够观测到的部分状态信息s1、s2，分别执行图2中绿色线标识的循环部分。训练过程中，评论家Critic1和Critic2可以获得全信息状态，同时还能获得所有Agent采取的策略动作a1、a2。

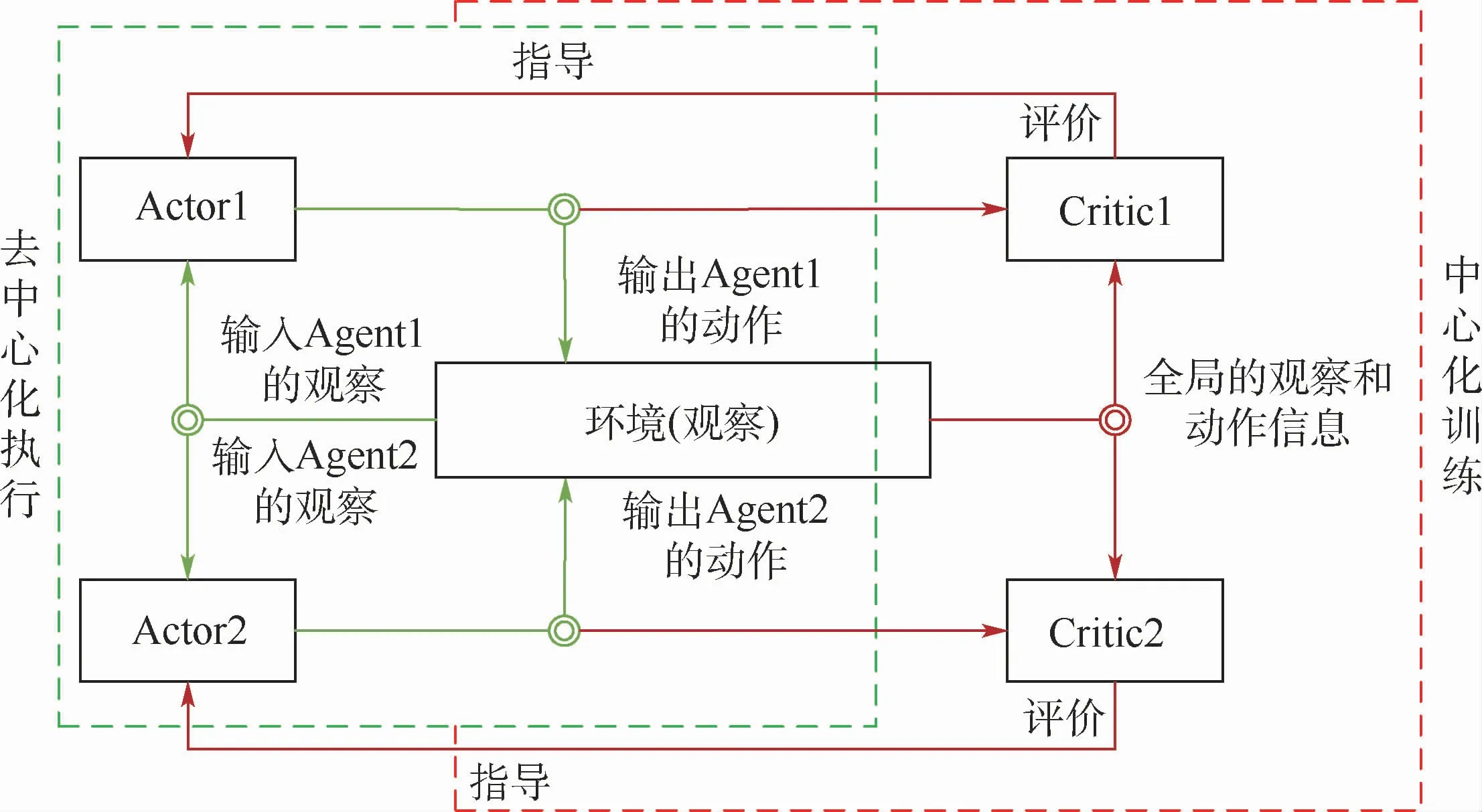
图2 MADDPG算法训练执行视图Fig.2 Training execution of MADDPG algorithm

2.2.4 Actor-Critic网络更新策略

如图3所示，在环境Evns中，智能体由Actor网络和Critic网络构成，这2个网络又分别包含目标网络（target-net）和估计网络 （eval-net）。Actor网络是卷积神经网络对策略函数π的模拟，参数为θπ。Critic网络是卷积神经网络对奖励函数Q的模拟，参数为θQ。

图3 MADDPG算法训练框架Fig.3 Training framework of MADDPG algorithm

Actor网络表示为

由此知道了所有智能体的动作，即使策略发生变化，那么环境也是静止的，随即通过梯度下降更新每个Agent的行为者Actor网络参数：

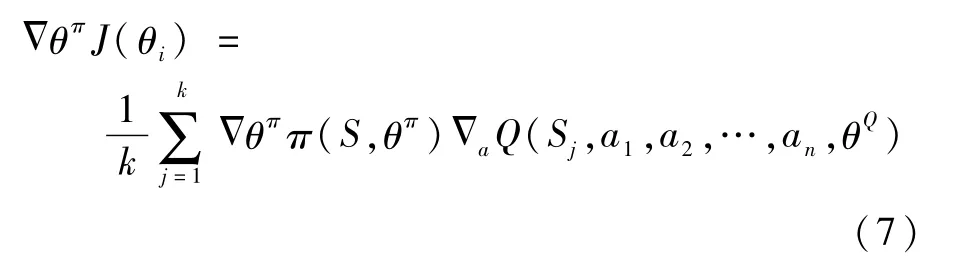
3 奖励机制的改进

3.1 奖励函数设置机制

在对抗任务中，多智能体的奖励不仅取决于自身策略，也取决于对手学习到的对抗策略，两者的策略学习速度未必同步，导致其奖励未必会持续升高，甚至出现波动和震荡［15］。由于智能体之间存在关系结构的约束，会对策略学习产生影响。如何设计一个无人集群系统合适的奖励信号来解决竞争对抗环境中智能体快速学习和稳定收敛，就成为了一个关键问题。

3.2 MADDPG算法奖励机制缺陷的实例

在捕食者i和逃逸者p实例中，MADDPG算法将对抗双方分别标识为捕食者和逃逸者，捕食者奖励机制是碰撞时碰撞者奖励值+10，不碰撞的时间内，惩罚值-1，逃逸者与此相反。这种奖励机制的好处就是捕食者和逃逸者的奖励值绝对值大小相同，双方的策略相反，因此二者的学习速度会逐渐达到同步，缓解了式（7）中Δθπ估计值方差波动和震荡，如表1所示。

表1 奖励机制设置Table 1 Reward mechanism setting

通过实验发现，MADDPG算法奖励信号太过疏松，最优解收敛效率低，即学习效率低，需要增加即时奖励信号，以增强学习效率。

3.3 基于环境信息的显式Per-Distance奖励机制

智能体和环境、其他智能之间的某些关系可以显式地描述，免除学习，并能够提供及时的学习信号。本文对MADDPG算法奖励机制进行改进，提出Per-Distance的智能体和环境之间显式关系的奖励机制、智能体之间关系的经验共享奖励信号，以提高学习的稳定性和效率。

3.3.1 智能体和环境关系的先验奖励信号

智能体执行早期获得的成功样本很少，导致经验池缺乏足够的学习经验用来调整策略。在Critic网络更新时，大部分时间里，捕食者回报值为rji＝-1，逃逸者的回报值为rkp＝1，Loss为α［R（s，a）+γmax Q′（s′，a′）-Q（s，a）］几乎没有变化（α为学习率），智能体做任意动作后的奖励值是相同的，Critic网络无法区分动作优劣，奖励函数不稳定，训练收敛速度很慢。为此，加入越界约束、智能体之间距离约束等先验价值，以提升奖励函数的收敛效率。

MADDPG算法的3V1围猎场景下，捕食者与逃逸者之间的距离为

实验发现，智能体经常出现越界情况，为提高计算效率，尽量保证智能体在设置的运行范围内产生对抗行为，对智能体越界想法进行限制。增加边界奖励，具体做法为：对逃出边界的智能体，施加较大的惩罚，惩罚大小取决于远离边界的程度。Per-Distance奖励机制中增加边界奖励B，保证智能体在环境范围内运动，不产生越界逃逸行为。设（xi，yi）为智能体i在二维环境中的坐标，0.9为智能体i的直径，如果该智能体离边界的最大距离小于0.9，则认为是超出边界，边界奖励值B＝0。如果智能体离边界的最大距离大于0.9，边界奖励值B给定一个智能体与边界距离有关的动态奖励值（max（xi，yi）-0.9）m，为任意给定的权重值，起到放大系数的作用，本文实验m＝200。

以捕食者为例，边界奖励B为

3.3.2 智能体之间关系的先验奖励信号

MADDPG算法的奖励机制，对抗双方的距离设定仅有2种状态，即D（i，p）＞0不碰撞或D（i，p）≤0碰撞。真实情况是：大部分时间对抗双方处于D（i，p）＞0不碰撞状态，需要很长时间才能训练得到最优策略，造成延迟奖励。

为解决延迟奖励问题，Per-Distance奖励机制中增加智能体之间独立计算的距离参数。不再是D（i，p）＞0不碰撞或D（i，p）≤0碰撞2种状态下的奖励值，改为根据距离可变动态设置奖励值，增加距离参数D（i，p）表示每个捕食者与逃逸者之间的距离，距离值在（-1，1）区间内变化，距离越大奖励ri越小，实现通过距离参数引导智能体快速地发生碰撞，以解决原算法中因距离状态过少而产生的奖励延迟问题。通过实验调参发现，距离参数0.1为最优，此时有利于Per-Distance奖励机制的稳定。

捕食者i的奖励机制为

相对于捕食者，逃逸者是反向奖励，只要逃离距离自己最近的捕食者，决策就是成功的，因此逃逸者只需要计算与自己距离最近的捕食者的距离并计算回报值。

逃逸者p的奖励机制为

在实验中发现，增加智能体之间距离动态关系的奖励机制，奖励值随捕食者和逃逸者之间的距离变化，奖励信号明显，智能体行为策略对应的动作区分明显，有利于奖励值收敛。说明考虑智能之间的关系对性能提高有明显影响。

3.3.3 增加智能体间经验值共享

MADDPG算法中，回报值Critic网络中共享容易造成最大值回报值的智能体的行为在群体中扩散，使得其他智能采取类似的策略。为了避免智能体策略的相似性，可以采取以下策略：

1）集中式训练，分布式执行模式的MADDPG算法是各智能体执行的队长，分配每个智能体行为。在Per-Distance奖励机制下，如果智能体的动作趋同，则同一动作的奖励值会降低，避免所有智能体采取同一行为去抓捕逃逸个体，防止整体抓捕效率下降。

2）随机化最大回报，将最大回报加上随机数r′∈（-1，1），每个智能体的回报值修改为r′r。

通过增加其他智能体对当前智能体的影响，同时，把价值引入到学习信号中，最终使得Critic网络在策略更新时能更好地识别出不同动作值之间奖励值的差异，提高学习的稳定性。

4 实验结果与分析

4.1 实验环境

实验设计是将原算法和改进后算法奖励曲线和智能体实际表现进行对比分析。

实验软件环境为Windows10操作系统；硬件环境为英特尔至强E78880v3*2型处理器、NVIDIA GTX 1080TI*3、64 GB内存；测试环境为OpenAI-gym，隐藏层为2层、隐藏单元个数为64的全连接神经网络构成的Actor、Critic网络及对应的目标网络和估计网络。

模型超参数设计为：Actor网络与Critic网络均采用采用全连接4层神经网络结构，隐藏层神经元数量 为64。每个Actor网络拥有单独的Critic网络，实验中发现，由于引入了距离参数，捕食者的距离参数值为负值，探索初期回报值将长时间停留在负数区间，而神经网络中的激活函数的负数域非常小，不利于训练，将神经网络输出层的激活函数去掉。

4.2 实验场景

Simple_tag实验场景是在对抗任务下智能体自主行为仿真，实验空间为二维有界密闭空间，包含4个智能体，其中，3个捕食者（蓝色），1个逃逸者（红色），实验场景描述如表2所示。

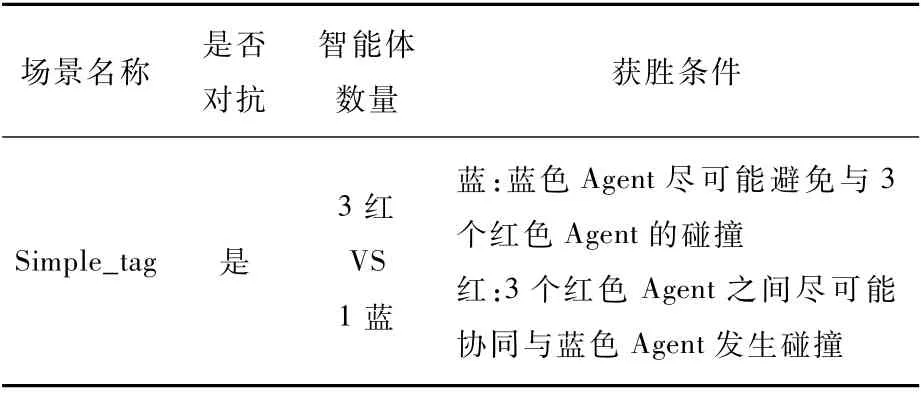
表2 3V1对抗实验场景Table 2 Experimental scenario of 3 versus 1 confrontation

实验参数设置如下：

1）捕食者和逃逸者作为智能形状大小忽略不计，视为质点。

2）坐标轴上智能体的运动范围为［0，20］。

3）3个捕食者合作共同追捕1个逃逸者。

4）捕获者速度上限为1.0/s，加速度上限为0.5/s2，逃逸者速度上限为1.3/s，加速度上限为0.7/s2。

5）当捕食者和逃逸者发生碰撞即间距为0时，视为捕获者捕获成功，逃逸者失败。

6）碰撞规则为碰撞后捕食者加速度减小，逃逸者加速度增大。

7）捕食者和逃逸者触碰到边界速度降为零。

4.3 实验分析

在不降低捕食者的捕获效果情形下，提升算法收敛速度和稳定性。捕食者分别将Per-Distance奖励机制放入MADDPG算法和DDPG算法进行学习训练。表3为经过20 000轮训练后，多智能体学习到的策略在1 000轮、60 000步随机实验下，捕食者执行每步动作后的平均碰撞次数。与原算法相比，看到加入Per-Distance奖励机制捕获效果更好，MADDPG相较于原算法平均碰撞次数提高了3.3%，DDPG算法平均碰撞次数提升幅度较小为1.7%。

表3 平均每步碰撞次数Table 3 Average number of collisions per step

对上述实验进行40 000轮的训练，利用TensorFlow的可视化工具TensorBoard描绘出捕食者和逃逸者的奖励值与训练次数之间的关系，对比MADDPG算法奖励机制和改进后的Per-Distance奖励机制的关系曲线。

图4～图6分别为捕食者1、捕食者2、捕食者3的奖励函数曲线。可以看出，引入距离参数，随道捕食者与逃逸者的距离增大，捕食者的奖励回报值减小，导致整体回报值呈降低趋势，奖励函数曲线下移。随着碰撞次数的增多，更多的直接奖励值开始叠加，使得奖励曲线下降趋势减缓并稳定下来。在改变奖励机制后，算法的收敛速度有较大提升，在5 000轮左右奖励值趋于平稳，奖励值在［2，4］区间内缓慢波动。通过实验证明捕食者奖励函数的收敛性、算法的稳定性提升十分明显。

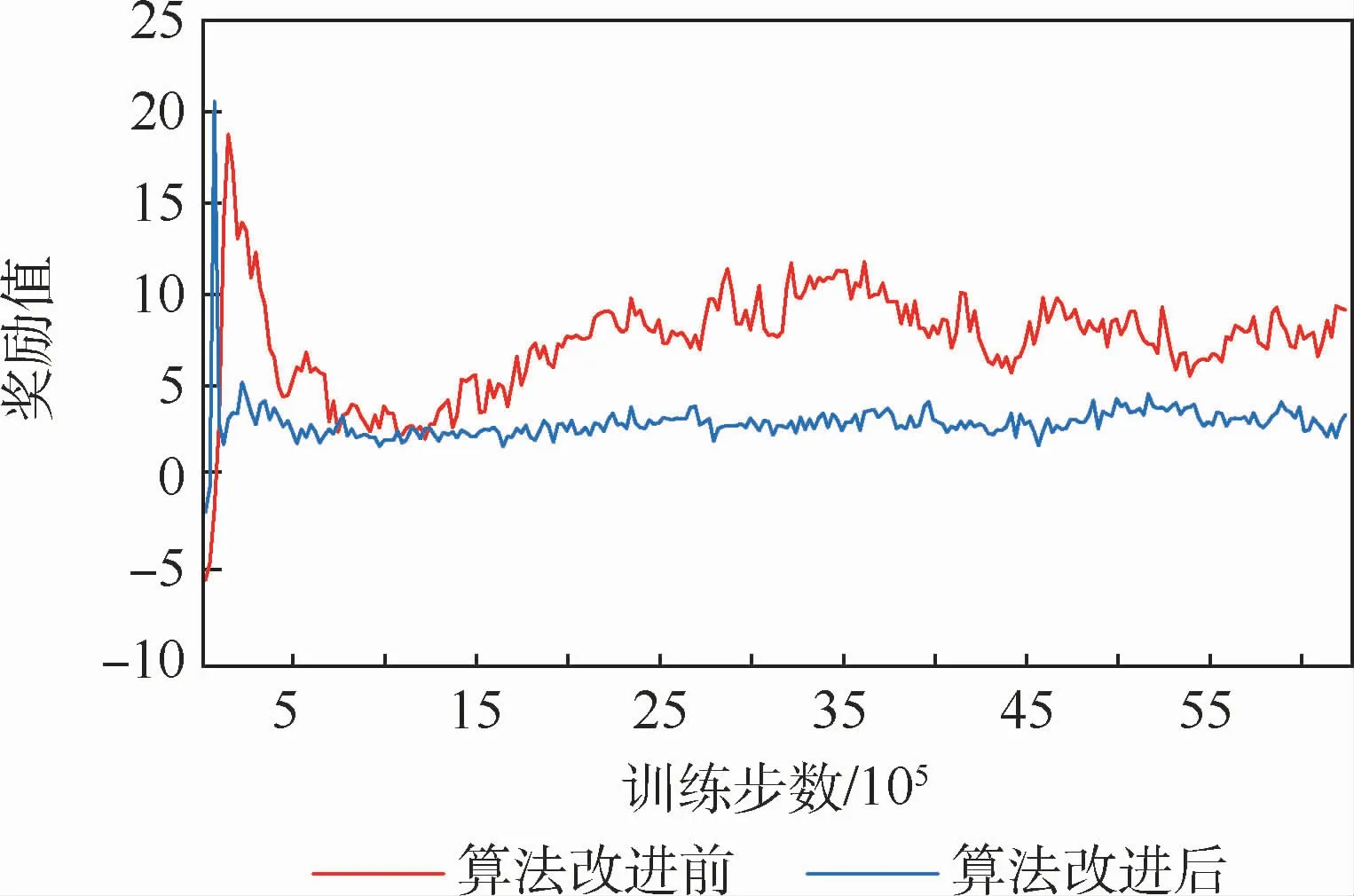
图4 捕食者1奖励函数曲线Fig.4 Curves of Predator 1 reward function

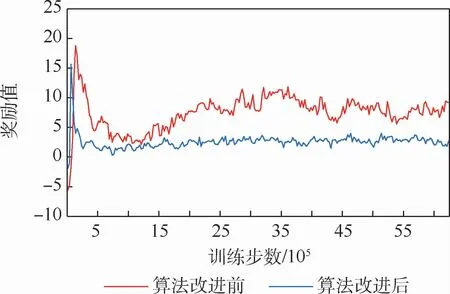
图5 捕食者2奖励函数曲线Fig.5 Curves of Predator 2 reward function

图6 捕食者3奖励函数曲线Fig.6 Curves of Predator 3 reward function

如图7所示，由于捕食者捕获效果的提升，逃逸者获得的负奖励（也称为惩罚）大大增加，导致奖励函数值减小。相较于捕食者收敛速度的明显改善，逃逸者奖励值的收敛速度改善效果不够突出，这是因为逃逸者要计算与捕食者中的最小距离，当离自己最近的捕食者更换时，策略网络要重新计算最小距离，更新步长较大，收敛性会打折扣。

图7 逃逸者奖励函数曲线Fig.7 Curves of escaper reward function

2种算法下，逃逸者的奖励值拐点都处于1 200 000步左右。在原来奖励机制下，逃逸者奖励函数的稳定性较差，奖励值在［-6，-15］的较大域值内上下浮动，函数曲线震荡幅度很大。引入Per-Distance奖励机制后，曲线波动幅度见减小，函数值在［-12，-16］的区间内变化，收敛性也有所提升。新的奖励机制对于逃逸者函数也有改进作用。

对上述实验中所有智能体的奖励值进行叠加，绘制出奖励值总和与训练轮步数的曲线，如图8所示。图8对比很明显，红色曲线显示原算法奖励值曲线在大范围波动，收敛性不好，引入Per-Distance奖励机制后，蓝色曲线显示奖励值曲线较早地进入到小区间波动，算法收敛性及稳定性得到了显著提升。

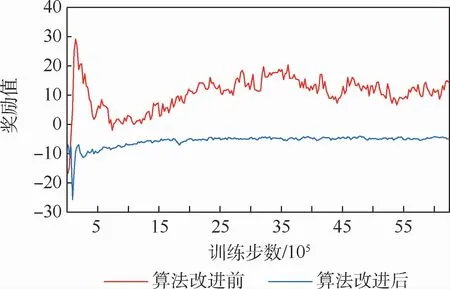
图8 奖励函数曲线总和Fig.8 Reward function curve sum

此外，为了进一步地评估Per-Distance奖励机制下算法的有效性，又与PES-MADDPG算法进行了奖励值与训练步数比较，如图9所示，依然是引入了Per-Distance奖励机制的PD-MADDPG算法奖励值收敛速度快，更快地趋于稳定。

图9 MADDPG、PD-MADDPG、PES-MADDPG算法奖励函数收敛性对比Fig.9 Reward function convergence comparison among MADDPG，PD-MADDPG and PES-MADDPG algorithms

上述实验中看到，在Per-Distance奖励机制下，智能体行为策略对应的动作区分明显，有利于奖励值收敛，说明考虑智能体的先验知识和智能体之间的关系对性能提高有明显影响。

4.4 Swarm Flow仿真平台

在陆军工程大学控制技术与智能系统实验室自主开发的智能陆战协同对抗仿真平台Swarm-Flow上训练改进后的算法，加载山地三维地图。图10为3架捕食者无人机围捕1架逃逸者无人机，实施一次围捕任务时三维可视化效果及围捕航迹图。图11和图12分别为捕食者无人机和逃逸者无人机一次任务的航迹。

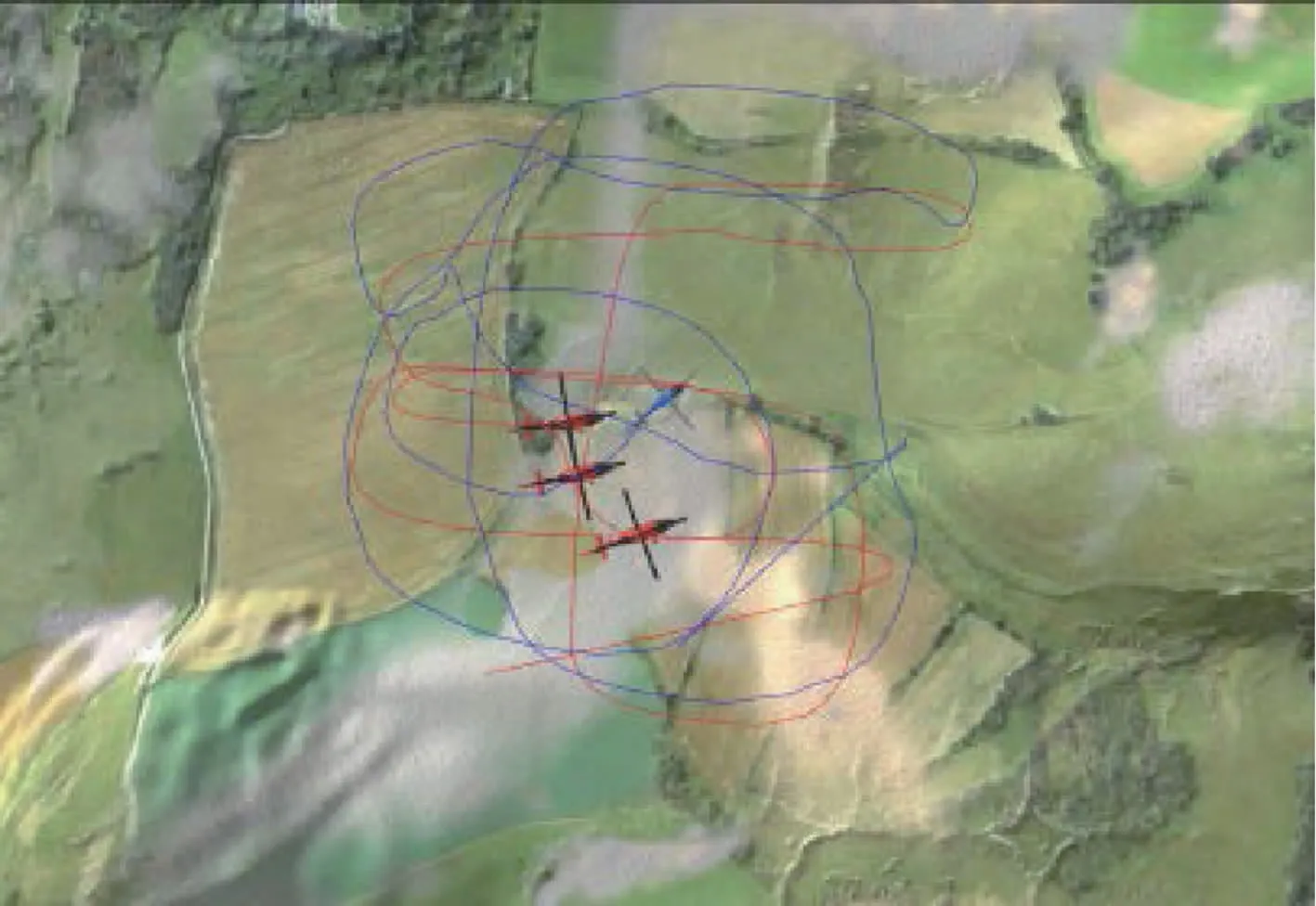
图10 对抗任务下双方航迹Fig.10 Track map of both parties under confrontation mission

图11 捕食者无人机航迹Fig.11 Predator UAV track map

图12 逃逸者无人机航迹Fig.12 Escaper UAV track map

图13为SwarmFlow仿真平台展示的陆战场景下，引入Per-Distance奖励机制的MADDPG算法，智能体3V1最终围捕效果。该算法可以推广至更多的智能体，算法对集群自主系统亦具有适应性。随着集群数量的增加，状态空间指数级增加，行为策略学习训练时间很长。图14展示了集群智能体20V6的围捕效果。

图13 智能体3V1围捕结果Fig.13 Result of agent 3V1 roundup

图14 智能体20V6围捕结果Fig.14 Result of agent 20V6 roundup

5 结束语

目前，将多智能体强化学习算法用于无人系统自主行为决策研究，最大的问题是算法收敛速度慢，使得在无人集群系统中的应用效果较差。

为了解决这一问题，本文着重研究了MADDPG算法的奖励机制，引入距离参数，提出Per-Distance奖励机制。在对抗任务下，改变回报值共享的方式，将对抗双方的距离奖励传递给执行智能体，解决延迟奖励问题。通过3V1围猎场景的仿真实验验证了改进的奖励机制实用性和优越性，提高了对抗任务下无人集群系统的群体行为策略学习效率。该算法可应用于集群对抗任务。

后期的研究中，考虑如何实现提升大规模集群行为决策效率问题。