基于损伤力学的含预腐蚀损伤铝合金的疲劳寿命预测
2022-01-15詹志新余洵胡伟平孟庆春
詹志新,余洵,胡伟平,孟庆春
(1.北京航空航天大学航空科学与工程学院,北京 100083; 2.深圳北航新兴产业技术研究院,深圳 518000;3.中国直升机设计研究所,景德镇 333001)
在机械与工程结构中,大多数构件受到的载荷并非静载,而是随时间循环变化的载荷,即循环载荷或交变载荷。在循环载荷的作用下,构件的承载部位会产生循环应力。研究表明,即使该循环应力远低于材料的强度极限,在经历一段时间的循环载荷作用后,构件也能够产生可见裂纹甚至会发生破坏。这种材料在循环载荷的作用下,所产生的性能逐渐退化直至完全失效的历程就是疲劳损伤破坏。在实际使用的工程材料及结构中,疲劳失效的现象非常显著[1-2]。在航空工业、压力容器、管道等相关的现代工业体系中,考虑到结构的复杂程度和对安全性的要求非常高,因此,解决相关的疲劳问题越来越重要。
在众多的疲劳问题中,腐蚀疲劳是一个非常重要的问题[3-4]。金属材料具有热力学不稳定性,当暴露在复杂的外环境中时,材料可能会在表面或者内部形成损伤,也就是腐蚀损伤[5-7]。对于设计人员来说,一方面,需要合理选择抗腐蚀材料以避免结构发生腐蚀;另一方面,需要考虑对结构的表面进行处理以减弱腐蚀所导致的负面影响。即便如此,防腐蚀设计还是很难保证不被腐蚀。一方面,机械构件的工作环境中一般都会有盐雾等腐蚀性物质;另一方面,在较长时间的使用过程中,表面防护层可能会破损,如受到外物的磕碰等,从而在构件表面产生预腐蚀坑,在蚀坑处会引起应力集中。在后续循环载荷的作用下,预腐蚀坑处会形成疲劳源,从而对材料的疲劳性能造成不利影响。谭晓明等[8]研究了不同程度腐蚀损伤对新型高强度铝合金疲劳裂纹萌生机制及扩展行为的作用。El May等[9]研究了腐蚀对高周疲劳强度的影响,发现预腐蚀试件的疲劳裂纹萌生于腐蚀坑,预腐蚀后试件的疲劳极限明显降低。刘治国等[10]通过开展航空铝合金试件模拟机场环境的加速点蚀试验,分析了航空铝合金点蚀形貌对应力集中系数影响。铝合金是容易引发点蚀的材料,Wang[11]、Burstein[12]及Arunachalam[13]等研究了金属材料蚀坑处的裂纹萌生及破坏规律,发现点蚀会带来构件表面的局部应力集中,点蚀坑处一般是疲劳裂纹源。因此,当预腐蚀损伤出现在承受循环载荷结构的表面时,为了确保其安全使用,必须分析研究材料或结构在预腐蚀损伤下的疲劳寿命。通过文献调研可知,金属材料和结构疲劳寿命预测的方法主要包括名义应力法[14]、局部应力法[15]、场强法[16]、临界平面法[17]、损伤力学方法[18]等,这些方法各有利弊。名义应力法不能考虑应力集中处的局部塑性,较难得到寿命预测的理想结果。局部应力法能够呈现加载顺序的影响,但很难反映局部应力梯度的影响。场强法在缺口疲劳寿命预测中,很大程度上取决于材料的性能。临界平面法在疲劳损伤计算中,往往将应变作为损伤参量,寻找使得损伤参量最大的平面。损伤力学方法通过损伤变量来分析材料性能在疲劳载荷下的劣化规律[19-20],其优点是物理意义相对清晰,通过文献调研可知,基于损伤力学的有限元数值解法是航空金属材料寿命预测的有效方法之一。
本文针对2024铝合金板的预腐蚀疲劳损伤问题,建立了含预腐蚀损伤铝合金疲劳寿命的预测方法。首先,推导了损伤耦合的弹塑性本构模型和多轴疲劳损伤演化模型,并给出了理论模型中材料参数的标定方法;然后,编写UMAT子程序,实现了损伤力学有限元数值计算方法;最后,建立了含预腐蚀坑铝合金板的有限元模型,预测了含预腐蚀坑铝合金板的疲劳寿命,并分析了预腐蚀时间对疲劳损伤演化及疲劳寿命的影响。
1 理论模型
1.1 损伤耦合的弹塑性本构模型
材料在加载条件和环境因素共同作用下,内部会萌生微孔洞及微裂纹等微观缺陷。在连续损伤力学理论中,往往以代表性体积单元(RVE)为研究对象,认为在RVE中某一方向的总截面面积为S,总的微观缺陷面积为SD,则损伤度[21]定义为总微观缺陷面积与总截面面积之比,即

式中:N为背应力分量的个数;Ck和γk为材料参数。
1.2 疲劳损伤演化模型
金属材料在经过预腐蚀后,往往在其表面产生预腐蚀坑,在后续循环载荷的作用下,疲劳裂纹会在预腐蚀坑处萌生。本节从预腐蚀坑的尺寸和初始损伤2个方面来分析预腐蚀对金属材料疲劳寿命的影响。预腐蚀坑的尺寸可以在一定的预腐蚀时间后通过测量仪去测量,考虑到在试件表面不同地方都会出现的预腐蚀坑,采用一个等效的分析方法,即找到试件表面上最大尺寸的预腐蚀坑,并在后续计算时,将预腐蚀坑预置在试件的最危险部位,即侧边上。由于预腐蚀会影响试件的化学性能、材料力学性能等,将这些影响统一用材料的初始损伤De来表示。根据预腐蚀的试验结果与数值计算的结果进行对比,可以确定出不同预腐蚀时间下材料的初始损伤。在初始损伤和预腐蚀坑尺寸这2个基本参数都确定后,就可以进行含预腐蚀构件疲劳寿命的计算。
Chaboche损伤演化模型[22]是一种常用的能够反映非线性损伤累积现象的模型。Chaudonneret[23]在单轴疲劳损伤模型的基础上,提出了多轴疲劳损伤演化方程:

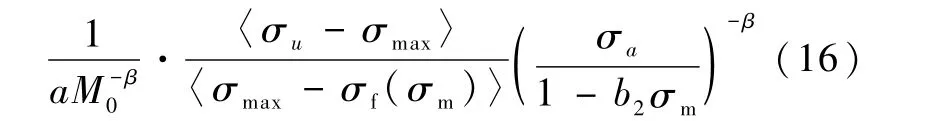
式中:σf为疲劳极限;σm为平均应力。
在工程应用中,疲劳危险部位的应力和应变多数情况是多轴的,多轴情况下,考虑由预腐蚀引起的初始损伤的疲劳损伤演化方程的表达式为

2 数值计算方法与材料参数的标定
2.1 计算方法
具体的计算过程如下:
1)初始化模型中所有的参数。
2)结合预腐蚀试件的疲劳试验数据,在不同的预腐蚀时间下,计算预腐蚀造成的初始损伤De。
3)采用ABAQUS软件,并结合编写的耦合损伤的弹塑性本构模型的UMAT子程序计算应力应变场。由于对每个循环都进行疲劳损伤的计算会非常耗时,在数值实现中采用了阶跃循环过程,假定在ΔN次循环期间,每个循环的循环应力和损伤增量保持不变。根据式(18)计算疲劳载荷下的损伤增量:

然后,计算相应的应力应变场和疲劳损伤场,直到疲劳裂纹萌生。
2.2 材料参数的标定
为了对预腐蚀损伤后的构件进行疲劳寿命预估,需要确定预腐蚀所造成的材料的初始损伤度及疲劳损伤模型中的材料参数。首先,开展静力试验,测得材料的静力力学性能;其次,对试件进行高周疲劳试验,得到材料的疲劳损伤参数;最后,进行试件的预腐蚀疲劳试验,并通过与数值计算结果的对比,得到材料的初始损伤度。
本文根据文献[24]中的静力拉伸试验,得到2024铝合金的静力性能参数,在表1中列出,其中,σs为屈服应力。根据无腐蚀标准试件的高周疲劳试验,标定5个疲劳损伤演化参数,即a、M0、β、b2、b1。第一步,基于标准光滑件的试验数据,得到参数β、b2、b1。其中,参数β和1/[(1+β)·a]可由应力比R=-1的疲劳试验数据确定。结合最小二乘法,根据其他疲劳载荷下的试验结果,标定参数b2和b1。第二步,选用损伤力学有限单元方法,对独立的参数a和M0进行标定。标定的所有参数在表2中列出。

表1 2024铝合金的静力力学性能参数Table 1 Static mechanical property parameter s of 2024 aluminum alloy

表2 标定的2024铝合金的疲劳损伤演化参数Table 2 Calibrated fatigue damage evolution parameters of 2024 aluminum alloy
简单介绍一下文献[24]中的2024铝合金的预腐蚀疲劳试验。①对2024铝合金板进行盐雾腐蚀试验。预腐蚀试验的试验环境是酸性盐雾环境,氯化钠盐溶液的浓度为5%,在盐雾腐蚀试验箱内进行,试验箱的温度为35℃左右,试件共分为3组,进行的预腐蚀时间分别为48 h、120 h和240 h。在完成预腐蚀试验后,观察不同预腐蚀时间下试件的预腐蚀坑尺寸,在后续的数值计算中,采用一种等效的分析方法,将每种情况下得到的最大尺寸的预腐蚀坑置在试件的危险部位,即侧边。②对预腐蚀试验后的标准试件进行疲劳试验,得到2024铝合金板在不同预腐蚀程度下的疲劳寿命。疲劳载荷的应力比为R=0.1。预腐蚀试件疲劳试验的结果及1组无腐蚀试件的疲劳试验结果如图1~图4所示。可以看到,与无腐蚀试件的疲劳寿命相比,预腐蚀后铝合金的疲劳寿命明显降低,说明预腐蚀试验使材料产生初始损伤。此外,电子显微镜下预腐蚀坑的形貌图片如图5[24]所示。根据预腐蚀试件的疲劳试验,并通过数值计算,得到了在不同预腐蚀时间下试件材料的初始损伤度,在表3中列出。

表3 不同预腐蚀时间下的2024铝合金的初始损伤度Table 3 Initial damage degree of 2024 aluminum alloy under different pre-corrosion time

图1 预腐蚀时间为0 h的疲劳试验结果Fig.1 Fatigue experimental results when pre-corrosion time is 0 h

图2 预腐蚀时间为48 h的疲劳试验结果Fig.2 Fatigue experimental results when pre-corrosion time is 48 h
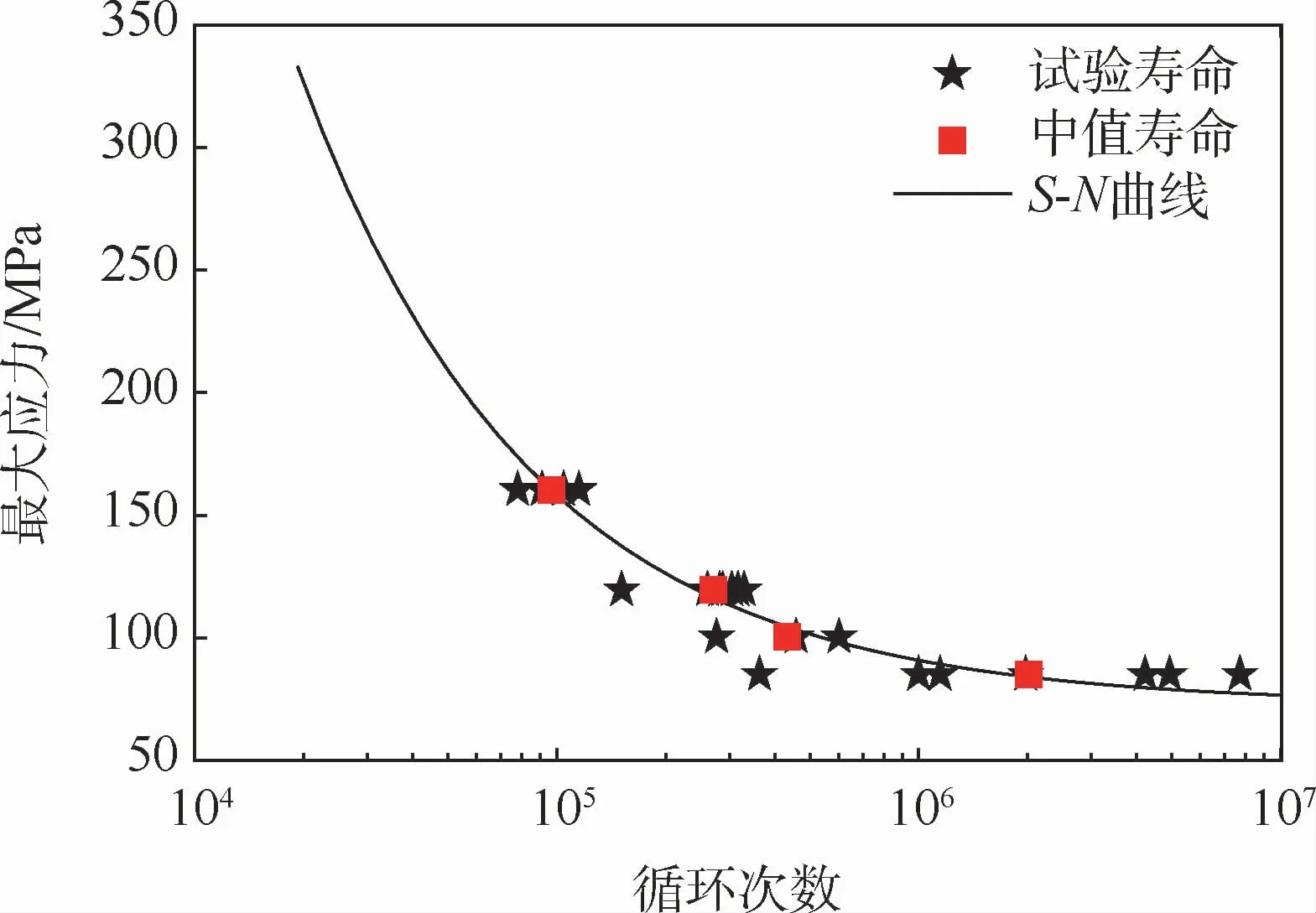
图3 预腐蚀时间为120 h的疲劳试验结果Fig.3 Fatigue experimental results when pre-corrosion time is 120 h

图4 预腐蚀时间为240 h的疲劳试验结果Fig.4 Fatigue experimental results when pre-corrosion time is 240 h

图5 预腐蚀后试件的电镜扫描图[24]Fig.5 Scanning electron microscopy photographs for pre-corroded specimens[24]
3 含预腐蚀坑的铝合金试件的疲劳寿命预测
预腐蚀完毕后,用电子显微镜对试件表面进行观察测量可知,在试件表面有腐蚀凹坑。用半球体近似模拟预腐蚀坑[25]。半球体的半径用r表示,预腐蚀坑的深度用c表示。假设在3种不同的预腐蚀时间(48 h、120 h和240 h)下所对应的预腐蚀坑的3种尺寸分别为:①r=0.25 mm,c=0.15 mm;②r=0.25 mm,c=0.20 mm;③r=0.25 mm,c=0.25 mm。对含预腐蚀凹坑的铝合金试件进行疲劳寿命预估。
3.1 含预腐蚀坑铝合金试件的有限元建模
在ABAQUS平台上,通过分析几何模型的对称性,构建四分之一的模型。采用三维8节点实体单元来进行网格划分,每个节点有3个方向的平移自由度。以深度为0.15 mm的预腐蚀坑为例,整个模型一共有22 386个单元,29 178个节点,划分完网格之后的模型如图6所示。数值解的精度与有限元网格的密度有很大关联,本文也对此进行了有限元网格的收敛性分析,确保数值解的准确性。对于预腐蚀时间为48 h、最大名义应力为120 MPa的情况,预腐蚀坑局部的损伤分布如图7(a)所示,危险单元的von Mises应力随着循环次数的变化情况如图7(b)所示。可以看到,损伤主要发生在局部区域,随着载荷循环的增加,单元的损伤逐渐增大,单元的刚度逐渐降低,承载能力下降,von Mises应力越来越小。

图6 含预腐蚀坑试件的有限元模型Fig.6 Finite element model of specimen with corrosion pit
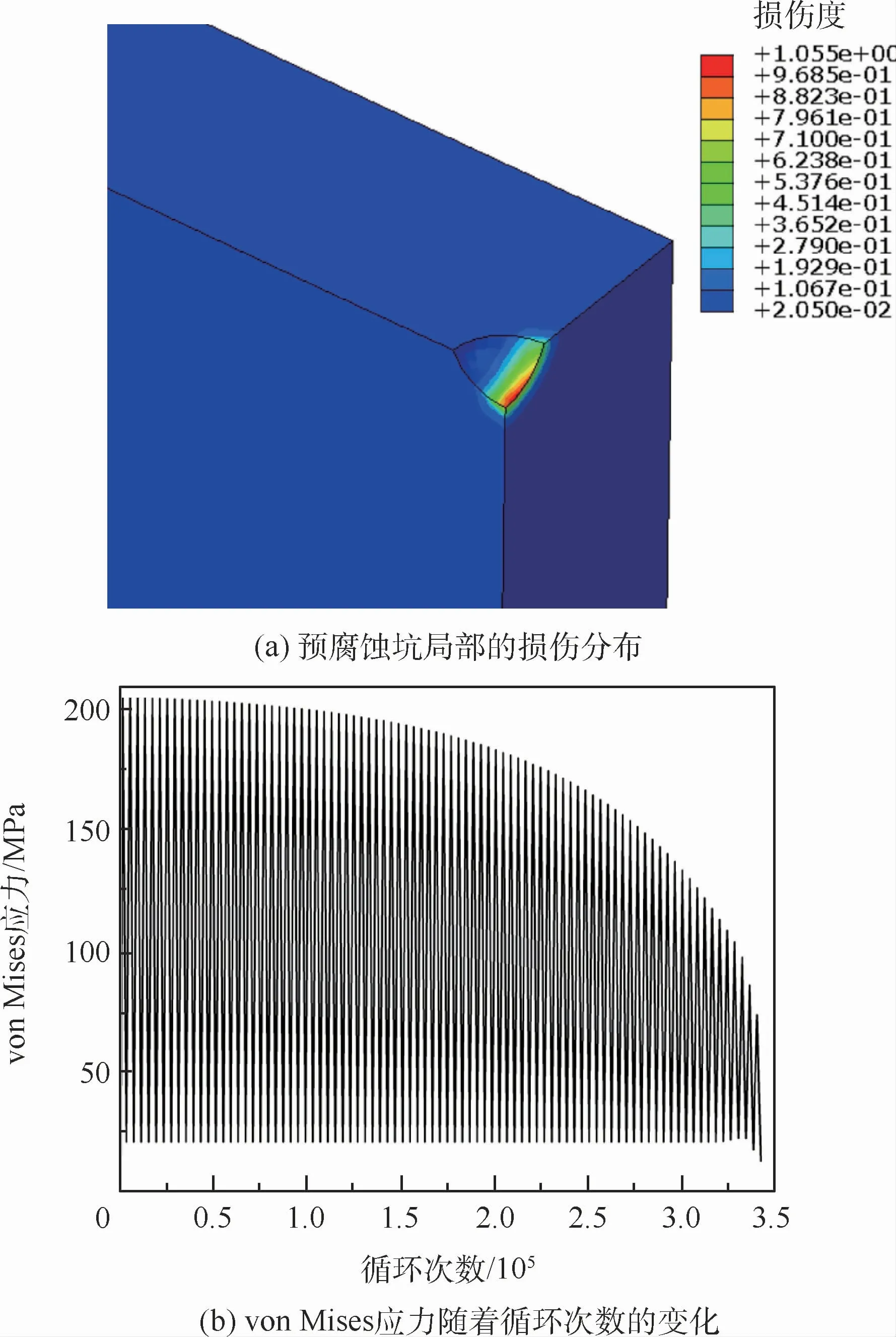
图7 损伤分布及应力演化趋势Fig.7 Damage distribution and stress evolution trend
3.2 疲劳寿命计算
在不同的预腐蚀时间下,根据不同的初始损伤度,计算得到的试件疲劳寿命在图8中给出。可以看到,在不同预腐蚀时间下,计算的铝合金疲劳寿命与试验中值寿命的误差多数位于2倍误差带范围内,并且几乎都在3倍误差带范围内,验证了上述方法的可行性。从对比的结果来看,预估疲劳寿命比试验寿命普遍偏低,主要可能的原因包括2个方面:①在数值计算过程中,所采用的预腐蚀坑的3种尺寸偏大,导致预腐蚀坑局部应力集中偏大,从而预估的疲劳寿命偏短;②将最大预腐蚀坑置于试件的最危险部位,而实际的最大预腐蚀坑位置并不都位于该位置。此外,当疲劳寿命越大时,预腐蚀坑尺寸和位置的影响越大,从而导致预估误差也越大。

图8 不同预腐蚀时间下的预估疲劳寿命与试验中值寿命的对比Fig.8 Comparison between predicted fatigue life and experimental median life under different pre-corrosion time
对于最大名义应力为120 MPa的情况,在3种不同的预腐蚀时间下,损伤度随着循环次数的变化趋势如图9(a)所示,弹性模量随循环次数的变化如图9(b)所示。可以看到,对于预腐蚀时间为48 h的情况,在前80%的载荷循环下,损伤度的增加较为缓慢;对于预腐蚀时间为120 h和480 h的情况,在前50%的载荷循环下,损伤度的增加较为缓慢。之后损伤度会剧烈增长,与此同时,弹性模量的降低也逐渐加快,材料的刚度越来越小。此外,预腐蚀时间越长,疲劳寿命越短,预腐蚀造成的初始损伤是一个主要因素。

图9 损伤度及弹性模量的演化Fig.9 Evolution of damage degree and elastic modulus
4 结 论
本文建立了基于损伤力学的含预腐蚀损伤铝合金的疲劳寿命预测方法,并以2024铝合金板为例进行了预腐蚀疲劳寿命预估,主要结论如下:
1)将预腐蚀对疲劳寿命的影响归结为2个方面,即腐蚀造成的材料初始损伤和腐蚀坑引起的应力集中。根据预腐蚀疲劳试验确定腐蚀造成的初始损伤,建立了损伤力学-有限元数值解法。
2)针对铝合金试件,根据文献中预腐蚀试验结果,采用等效的分析方法,在试件侧边预制最大尺寸的预腐蚀坑,通过数值计算与试验结果的对比,确定预腐蚀引起的初始损伤度,建立含预腐蚀坑的试件有限元模型,采用损伤力学-有限元数值解法给出疲劳寿命计算结果。
3)对于铝合金板的预腐蚀试件,与无腐蚀试件的疲劳寿命相比,预腐蚀后的铝合金疲劳寿命明显降低,在预腐蚀48 h后,其寿命降低速率最大,增加腐蚀时间,寿命降低的速率变小。在腐蚀到一定程度后(预腐蚀48 h),腐蚀产物在表面形成了一层保护层,阻止了腐蚀介质与新的腐蚀面接触,延缓了腐蚀速度,从而疲劳寿命降低的速率也减小。
本文对于验证模型可行性的试验部分仅选用了2024铝合金,未来将开展更多金属材料的预腐蚀疲劳试验,并用本文中的模型及数值方法进行寿命预测,来进一步验证本文提出的含预腐蚀损伤疲劳寿命预测方法及疲劳损伤模型,并推及到其他金属材料,以研究该模型和方法对其他材料疲劳损伤分析的适用性。
