基于抗冻性指标的玄武岩纤维再生混凝土的寿命预测*

侯永利，吕东朔，周磊磊，杨新宸睿

(1.内蒙古工业大学 土木工程学院，呼和浩特 010051；2.内蒙古自治区土木工程结构与力学重点实验室，呼和浩特 010051；3.内蒙古自治区建筑检测鉴定与安全评估工程技术研究中心，呼和浩特 010051；4.山西四建集团有限公司，太原 030012)

0 引 言

在我国北方寒冷地区，由于昼夜温差及季节性温度变化，使混凝土构件长期受到冻融循环作用，影响其耐久性，造成巨大的经济损失[1]。再生粗骨料因原生混凝土损伤积累过程与破碎过程而产生的微裂缝，不仅增大了再生混凝土的吸水率[2]，而且为水分入侵混凝土提供了新的通道[3]，致使再生混凝土更容易产生冻融破坏，因而再生混凝土的抗冻性通常较差。研究表明[4-6]，掺入适量的BF能够有效提高混凝土的抗冻性能。

对BFRC的抗冻性能进行预测，可有效节约试验成本与时间。当前，众多学者基于冻融循环次数建立宏观模型，如用抗压强度作为损伤变量而建立的损伤模型[7-8]，但测试抗压强度通常需要破坏试件，难免造成资源的浪费；也有相关学者利用细观损伤变量建立模型[9-11]来描述混凝土的损伤，如Jin[9]和Tian[10]分别基于分形维数以及内部孔隙结构演化建立细观冻融损伤模型，但混凝土的非均匀性导致微细观的取样难度加大，影响模型的精确度。通过线性拟合可知，经历冻融循环后混凝土的相对动弹性模量既与混凝土受拉压的峰值应力、峰值应变和受拉初始弹性模量等力学性能具有良好的相关性[12]，同时相对动弹性模量又作为一种易测而又直观的宏观参数，可以直接作为损伤变量来建立模型[8,13]，进行混凝土抗冻性的预测。

灰色系统理论可以针对“小样本、贫信息”的数据进行科学的预测。林跃忠[14]、杨璐[15]等虽利用灰色系统理论的GM(1,1)模型的均值形式对普通混凝土以及再生混凝土进行抗冻性的预测，但仅采用GM(1,1)模型的均值形式预测混凝土的相对动弹性模量，仍具有局限性。本文基于BFRC抗冻性能的试验结果，结合GM(1,1)模型的ODGM、EGM、EDGM、DGM 4种形式对BFRC的抗冻性能进行预测，并对4种模型的预测精度以及模型所预测的使用寿命进行比较分析。

1 实 验

1.1 试验原材料

再生粗骨料源于废弃的路面，通过机械破碎、人工筛分形成4.75～26 mm碎石；呼和浩特市冀东水泥厂生产的水泥(P·O42.5)；细骨料采用河砂，表观密度为2 630 kg/m3，细度模数为2.7；BF长度为20 mm，其物理力学性质如表1所示；呼和浩特市自来水；聚羧酸系高性能减水剂，减水率不低于25%。

表1 玄武岩纤维的物理力学性质

1.2 再生混凝土配合比设计与制备

配合比参照《公路水泥混凝土路面施工技术细则》(JTG/T F30—2014)确定，与原生混凝土相比，25%取代率的再生混凝土的力学性能与耐久性下降幅度较低[16-20]，故选用再生粗骨料取代率为25%，BF掺量分别为0、0.1%、0.2%、0.3%，依次编号为BFR0、BFR1、BFR2、BFR3，配合比如表2所示。

表2 再生混凝土配合比

搅拌过程：将水泥、细骨料投入搅拌机内，干拌3 0 s混合均匀；将加入减水剂的拌合用水投入到搅拌机内，再次搅拌60 s；加入BF，搅拌30 s后加入粗骨料，搅拌180 s，然后浇筑成型，试件尺寸为100 mm×100 mm×400 mm。

1.3 测试方法

参照《公路工程水泥及水泥混凝土试验规程》(JTG 3420—2020)，使用NJW-HDK-9微机全自动混凝土快速冻融试验机，按照快速冻融法进行试验，每25次冻融循环停机检测混凝土的共振频率以及质量变化，其中共振频率采用美国NDT共振频率测定仪测定，当试件的相对动弹性模量下降到60%、质量损失率达到5%或者达到225次冻融循环的时候，停止试验。

2 结果分析与GM(1，1)模型建立

2.1 结果分析

图1(a)为不同BF掺量的BFRC在225次冻融循环过程中质量损失率的变化情况。由图1(a)可知，对于未掺入BF的BFR0，25次冻融循环之后质量损失率就开始增长。而掺入BF之后，经50次冻融循环之后，质量损失率才开始增长，随着冻融循环的进行，各试样质量损失速率逐渐加快，75次冻融循环之后，4条曲线开始出现明显的“分层”，从75次到225次冻融循环过程中，4条曲线自下而上依次对应的纤维掺量为0.3%、0.2%、0.1%、0。经历225次冻融循环之后，BFR0到BFR3的质量损失率依次为1.41%、0.94%、0.77%、0.55%。这说明BF的“拉结”作用可抑制BFRC的质量损失。

图1(b)为不同BF掺量的BFRC在225次冻融循环过程中相对动弹性模量损失量的变化情况。通过图1(b)可知，随着冻融循环的进行，各曲线的斜率不断增大，说明BFRC的相对动弹性模量的衰减速率逐渐加快，但从75次到225次冻融循环过程中可看出，4条曲线呈现出与图1(a)相同的“分层现象”，225次冻融循环之后，BFR0到BFR3的相对动弹性模量分别损失18.7%、14.3%、12.4%。9.8%。说明随着BF的不断掺入，BFRC的相对动弹性模量的损失速率在逐渐减缓。故综合分析图1可知，BF的掺入有助于提高BFRC的抗冻性能。

图1 BFRC抗冻性能试验曲线

2.2 建立GM(1,1)模型

灰色系统理论是通过建立与原始数据相关的模型，挖掘、发现、掌握系统的演化规律，从而实现对未来变化的定量预测[21]。本文基于GM(1,1)模型进行预测，GM(1,1)模型表示含有一个变量的一阶微分方程的动态模型，主要有4种基本形式：均值GM(1,1)模型(EGM)、原始差分GM(1,1)模型(ODGM)、均值差分GM(1,1)模型(EDGM)以及离散GM(1,1)模型(DGM)。

将冻融环境下某纤维掺量的BFRC经历225次冻融循环(每隔25次冻融循环进行检测)所测的相对动弹性模量作为原始序列，记为X(0)，即

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(1)

将原始序列X(0)进行一次累加，得到新序列X(1)，则

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

(2)

将利用表3求得的模型参数汇总于表4。通过表4可知，各预测模型参数均满足“-a<0.3”的要求，因此选用的模型可以实现对BFRC的中长期预测[22]。

表3 GM(1,1)模型参数的解析式

表4 灰色预测模型参数

结合式(3)求出各模型的解析式并经累减还原即可得到各模型的预测值，将实测值及所求预测值汇总于表5。

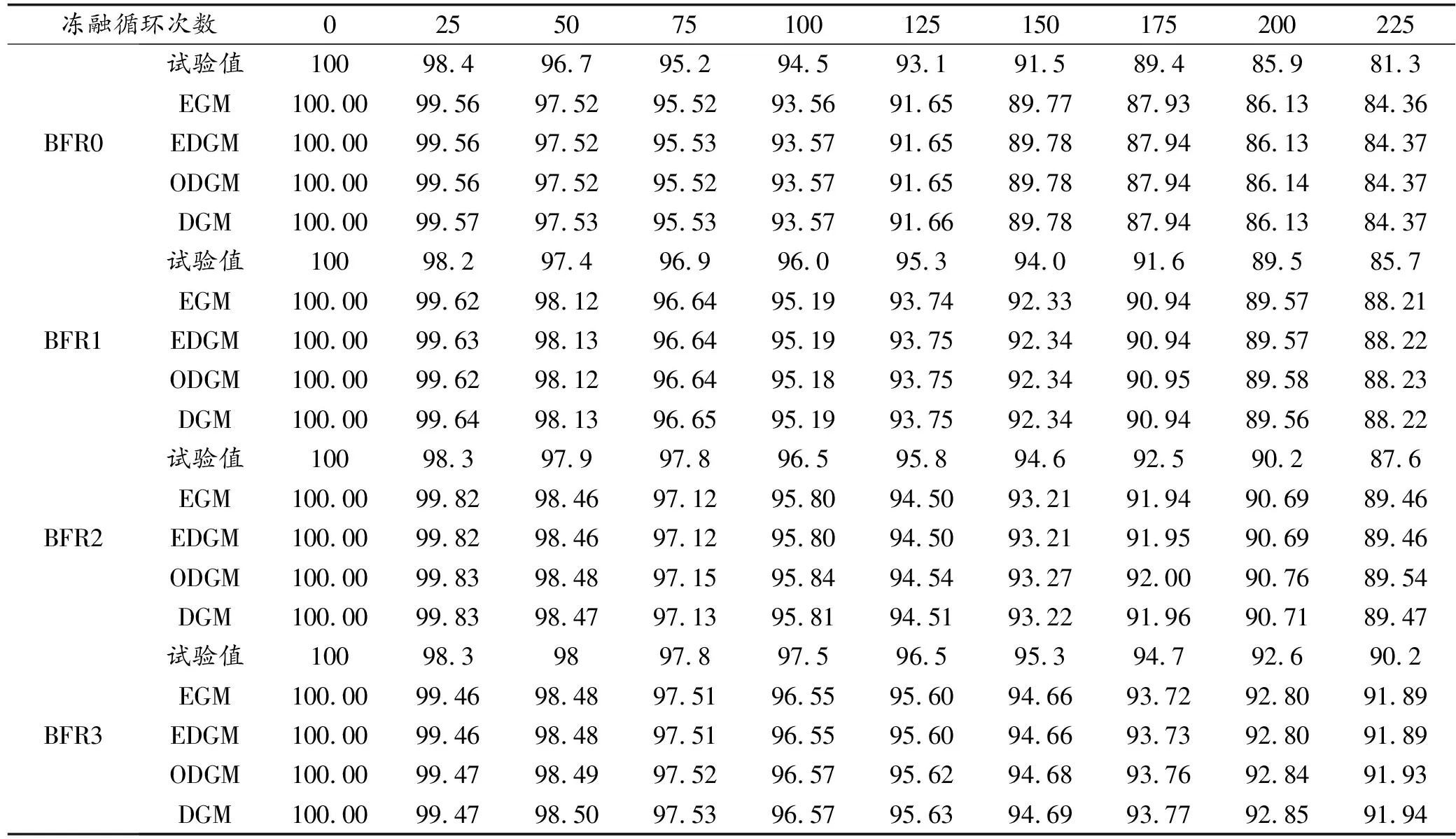
表5 模型预测值

(3)

2.3 GM(1,1)模型精度检验

设模型计算所得到的模拟序列为

(4)

(5)

(6)

(7)

均方差比值

(8)

小误差概率

(9)

利用前225次冻融循环的相对动弹性模量的模拟值，将计算所得的均方差比值C、小误差概率p等结果汇总于表7。根据表6中的精度评定结果可知，4种模型的均方差比值C均小于0.35，小误差概率p均大于0.95，因此4种预测模型对不同纤维掺量的BFRC的预测精度均为Ⅰ级[21]。

表6 精度检验等级参照表[21]

表7 模型精度评定表

为进一步比较各模型的精度，引入相关系数R2，计算见公式10，结果见表8。相关系数R2越大说明模型的精度与拟合程度越高，为便于比较，分别将BFR0、BFR1、BFR2、BFR3中各模型的R2按从大到小的顺序以1、2、3、4进行赋值，对各模型的精度进行统计分析，分析结果汇总于表9。

表8 R2计算结果

表9 R2统计分析

(10)

利用表8、9中R2的计算值与统计分析结果进行综合分析可知，当BF掺量不低于0.2%时，此时参照BFR2和BFR3的统计结果，可以看出，EGM的精度稳居4种模型的首位，EDGM的精度略低于EGM，尽管ODGM、DGM的赋值结果呈现出一定的波动趋势，但二者的精度要低于EDGM和EGM。当BF掺量不超过0.1%时，参照BFR0、BFR1的统计结果，4种模型的精度从高到低依次为DGM、EGM、EDGM、ODGM。倘若纤维掺量介于0.1%到0.2%之间，参照BFR1和BFR2的试验结果，EDGM、ODGM模型的精度应分居4种模型的三四位，而EGM模型精度略高于DGM。综上所述，倘若预测过程中需考虑模型精度，当BF掺量不超过0.1%时，建议使用DGM模型进行BFRC抗冻性的预测，反之，可用EGM模型进行预测。

2.4 寿命预测与分析

有调查研究[23]表明，不同地区的室内外的冻融循环次数可按如下关系式进行转换：

(11)

式中：t表示混凝土结构的室外地区的使用寿命(a)；k为试验系数，即室内冻融循环一次相对于室外自然冻融循环的次数，一般为10～14，本文取平均值12；N为室内的冻融循环次数；M为混凝土结构在室外环境下一年可能经受的自然冻融循环次数(次/年)。

经统计，内蒙古地区的年均冻融循环次数为120次[23]，参照《公路水泥及水泥混凝土试验规程》(JTG3420—2020)，以相对动弹性模量下降到60%作为BFRC经历冻融循环的“失效准则”，结合模型的预测结果，利用公式(11)即可得到基于本文试验条件下的BFRC在内蒙古地区受冻融循环单因素作用的寿命预测年限，汇总于表10。

通过表10中的寿命预测结果发现，即使未掺入BF，再生混凝土的抗冻性也完全满足《公路水泥混凝土路面设计规范》(JTG D40—2011)中一级公路或高速公路规定的30年的基准期的要求，掺入不高于0.3%的BF以后，再生混凝土的寿命预测值逐渐增加，这主要因为BF与基质材料紧密结合，承担部分冻融循环产生的拉应力，并有效地阻止了混凝土内部裂缝的产生、扩展与贯穿，延缓混凝土的冻融损伤进程。

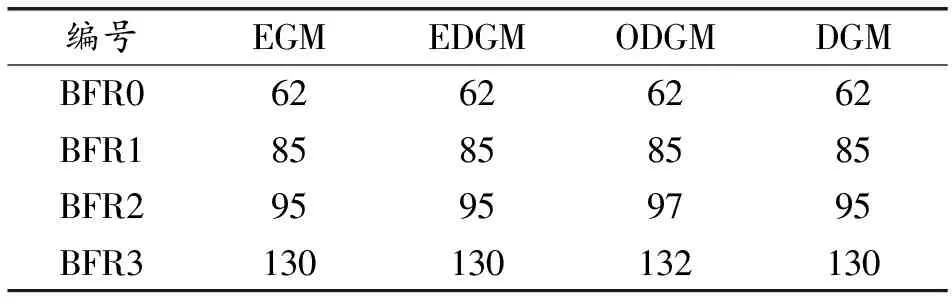
表10 内蒙古地区BFRC的寿命预测表

另一方面，EGM、EDGM、DGM的寿命预测结果相同，但对纤维掺量分别达到0.2%与0.3%的BFR2和BFR3进行寿命预测时，ODGM模型的预测结果与其余模型偏差较大，且预测结果较为激进，这说明ODGM模型在长期寿命预测方面存在不稳定因素，因此不建议用ODGM模型预测BFRC受单因素冻融循环作用的使用年限。

3 结 论

(1)随着BF掺量的增加，相对动弹性模量的衰减速率以及质量损失率的增加速率得到减缓，BFRC的抗冻性能逐渐提高。且通过计算可知，BFRC的抗冻性完全符合《公路水泥混凝土路面设计规范》(JTG D40—2011)中一级公路或高速公路30年的设计要求。随着纤维掺量在一定范围内逐渐增加，BFRC的寿命逐渐增加。

(2)基于试验数据及灰色系统理论建立了BFRC的抗冻模型，尽管4种模型精度均达到Ⅰ级，但模型的精度存在略微差异，故引入相关系数R2，结合赋值的方法对各模型精度进行比较分析后发现，倘若只考虑模型精度，在BF掺量超过0.1%时，建议采用精度较高且更加稳定的EGM进行混凝土抗冻性预测；相反，当BF掺量不高于0.1%时，可采用预测精度最高的DGM进行预测。

(3)通过对寿命预测结果的比较分析可知，建议使用EGM、EDGM、DGM 3种模型预测BFRC受冻融循环单因素作用的使用年限，ODGM模型可能存在预测激进的较大偏差，存在不稳定因素，故不建议使用。