聚丙烯-钢纤维/再生粗骨料混凝土力学性能正交试验研究*

金宝宏，郑传磊，侯玉飞，王晋浩，赵亚娣，李淑翔

(1.宁夏大学 土木与水利工程学院，银川 750021；2.宁夏大学 新华学院, 银川 750021)

0 引 言

石子(NCA)作为配置混凝土必不可少的材料，其储量和质量影响着城市建设和社会经济的发展。随着城市建设脚步的加快，石子作为地球上的不可再生资源，被开采的数量逐年增多，盲目开采造成骨料资源枯竭和发生了一系列诸如山体滑坡、河床改道和泥石流等自然灾害问题。废弃混凝土作为城市建设产生的建筑垃圾，目前除少数被用来垫地基以外，其余处理方式以垃圾场填埋和郊区露天堆放为主。为了保护环境和减少资源浪费，有必要研究将废弃混凝土回收使用，制作成新混凝土的原材料。

废弃混凝土经破碎、筛分和分级等工序处理后得到的再生骨料，部分或全部替代砂石拌制成的再生混凝土，其性能弱于普通混凝土[1-3],但在某些对于强度要求较低的混凝土工程中，还是足够使用。为了增大再生混凝土的应用范围，众多学者对增强再生混凝土的性能做了大量研究工作[4-6]。研究发现，通过掺入纤维对增强混凝土的性能具有显著的作用，掺入不同的纤维对增强性能的表现形式不同，而合理的掺入两种及以上纤维可以弥补单一纤维增强性能的局限性，有效发挥正混杂效应，使混凝土的性能相比掺入单一纤维得到更大增强[7-9]。权长青[7]将不同掺量的聚丙烯纤维(PP)和钢纤维(SF)掺入混凝土中，结果表明，混合纤维对增强混凝土力学性能的效果较为显著。高丹盈[8]研究高温状态下PP-SF高强混凝土的抗爆裂能力和强度变化，结果表明，混合纤维相比单一纤维能有效抑制高强混凝土的高温爆裂，有效增强高强混凝土在常温时和高温后的弯折强度。霍俊芳[9]研究PP-SF对再生混凝土抗冻性能的提升作用，结果表明，适量掺入PP-SF会增加混凝土的含气量，改善孔结构，增强抗冻性能，并且掺混合纤维的混凝土其抗冻性能明显强于掺单一纤维的混凝土。

PP价格低廉，质轻，延展性和耐久性好，具有稳定的化学及物理性质，但其弹性模量和强度较低。SF虽然价格较贵，耐久性差于PP，但其弹性模量和强度高。将PP和SF混合掺入混凝土中得到的PP-SF混凝土的力学性能和工作性能优异，且造价较为低廉。

目前国内外关于PP-SF混凝土的研究较多[7-11]，而关于将PP-SF混合掺入再生混凝土中的研究较少。在本项研究中，笔者将PP-SF和再生粗骨料(RCA)掺入混凝土中用以制备PP-SF/RCA混凝土，研究PP体积分数、SF体积分数和RCA质量分数对混凝土力学性能的影响，应用正交试验法对PP-SF/RCA混凝土的力学性能进行全面的实验与分析评估。

1 实 验

1.1 实验原材料

实验所用水泥为赛马牌42.5R普通硅酸盐水泥，其初凝和终凝时间分别为142和198 min，3和28 d抗压强度分别为28.2和48.7 MPa。粉煤灰为当地火电厂生产的Ⅰ级灰，其细度、比表面积、烧矢量和需水量比分别为5.1%(>45 μm)、510 m2·kg-1、1.83%和94%。砂为银川市兰山砂石厂人工水洗中砂，其表观密度、堆积密度、空隙率、泥浆含量和细度模数分别为2 718、1 630 kg·m-3、40%、1.2%和2.94。减水剂为北京慕湖公司生产的HWR-S型聚羧酸系高效减水剂(粉剂)，减水率约为20%。水为银川市城市自来水。PP为上海影佳公司产品，图示见图1(a)。SF为衡水普方公司产品，图示见图1(b)。NCA为银川市兰山砂石厂生产的碎石，图示见图1(c)。RCA为原始强度C30的路面板状废弃混凝土经处理得到的碎石，图示见图1(d)。PP和SF主要性能参数见表1，NCA和RCA主要性能参数见表2。

图1 PP、SF、NCA和RCA的外观

表1 PP和SF主要性能参数

1.2 试验方案设计

按照L16(45)正交表设计三因素四水平正交试验, 设两列空白列，设计强度C30。因素水平见表3，基准混凝土配合比见表4。试验时通过调整减水剂的用量使塌落度近似50 mm，经过多次试拌，最终确定用水量为156 kg·m-3、水胶比为0.49、粉煤灰替代率为20%、砂率为37%和减水剂掺量为0.05%～0.6%。

表3 因素水平表

表4 基准混凝土配合比(kg/m3)

1.3 混凝土试件制作

试验共设计1个基准组(J-0)和16个正交组(ZJ-1～16)，根据试验需要，每组制作9个100 mm×100 mm×100 mm立方体试件和3个100 mm×100 mm×400 mm棱柱体试件，用于测试7 d抗压强度和28 d抗压、劈拉及弯折强度。

为使PP和SF在混凝土中均匀分布，搅拌时边搅拌边加PP和SF，并充分预留干拌时间。搅拌前使用干净湿抹布擦拭搅拌机和塌落度桶内壁，按照砂、水泥、粉煤灰、NCA、RCA、SF、PP的先后次序依次材料倒入搅拌机内，干拌90 s；加入水和减水剂，搅拌90 s；搅拌结束后将混合物倒入塑料模具，在振动台上振捣抹面，室温静置24 h后将试件脱模，再将试件移入标准养护室养护7和28 d。

2 实验结果

2.1 混凝土试件破坏形态

2.1.1 抗压强度试件破坏形态

图2为试件的抗压强度破坏形态。通过观察试验可知，ZJ-(1～16)在加载过程中的试验现象与J-0类似，ZJ-(1～16)随着纤维掺量的增加，试件表面裂缝出现的时间有所延后。试验开始时，试件首先在中部和底边角处产生微小裂纹；随着荷载的增加，裂纹逐渐扩展成裂缝，并开始横向膨胀，底边角及中部表层混凝土出现开裂、剥落现象；在加载的后期，试件表面相邻短裂纹开始贯通连结，试件内部形成数条长裂缝；加载结束后，J-0侧面破碎并发生整体剥落，表层混凝土剥落严重，如图2(a)所示；ZJ-(1～16)由于掺入了一定量的PP和SF，虽然裂缝虽然比J-0多，但大多为小裂缝，且贯通式裂缝较少，如图2(b)、(c)和(d)所示。试件的纤维体积分数越高，底边角及中部表层混凝土剥落越少，试件整体性越好。试件受到破坏时，PP和SF在混凝土中能起到桥接和应力传递作用，能改善应力分布，在裂缝处形成一道道连接，约束试件受压时产生的横向膨胀，有效遏制裂缝的进一步发展，继而提高试件的抗压强度。

图2 抗压强度破坏形态

2.1.2 劈拉强度试件破坏形态

图3为试件的劈拉强度破坏形态。在劈拉破坏加载的前期，试件处于弹性阶段；随着荷载的增加，试件首先在两端垫条处产生裂纹，并逐渐向试件中部扩大，最终伴随着“嘣”地一声，试件被劈裂。J-0脆性较大，在达到破坏荷载后，试件被直接劈成两半，其断裂面呈现“Ⅰ”型，如图3(a)所示。ZJ-(1～16)在被劈裂时的响声相较J-0较为沉闷，相较J-0没有被劈成两半，试件表面大都呈现出一条较粗长裂缝和数条较细短裂缝，仔细观察裂缝可以看到试件内部仍有部分纤维连接，如图3(b)、(c)和(d)所示。

图3 劈拉强度破坏形态

2.1.3 弯折强度试件破坏形态

图4为试件的弯折强度破坏形态。弯折破坏加载前期试件无明显形变，随着荷载的增加，伴随着“嘣”地一声，试件瞬间被折断。J-0最终被折成两段，而ZJ-(1～16)由于加入了PP和SF，韧性有所增强，试件下端仍有部分连接，如图4(a)和(c)所示。观察J-0的破坏面可见断裂面较为平整，既有骨料与砂浆界面间的黏结破坏，也有再生骨料被劈开，为明显的脆性断裂现象，如图4(b)所示。图4(d)中试件断裂面凹凸不平，随机分布着形态各异的PP和SF。

图4 弯折强度破坏形态

2.2 混凝土力学性能

表5是J-0和ZJ-(1～16)的正交试验结果。从表5可以看出，ZJ-(1～16)的力学性能均大于J-0，7 d抗压强度ZJ-2最大，28 d抗压强度ZJ-4最大，劈拉强度ZJ-3最大，弯折强度ZJ-16最大，较J-0分别提高41.9%、23.0%、59.1%和28.9%。通过对正交试验结果进行分析，得到VP、VS和RR三因素关于7 d抗压强度和28 d抗压、劈拉及弯折强度的极差与方差分析结果如表6和7所示。表6中7 d抗压强度的极差小于空白列(D)的极差，其试验结果存在可行度不足；28 d抗压、劈拉及弯折强度的极差均大于空白列的极差，试验结果可信[12]。图2是VP、VS和RR三因素对PP-SF/RCA混凝土7 d抗压和28 d抗压、劈拉及弯折强度的影响图。

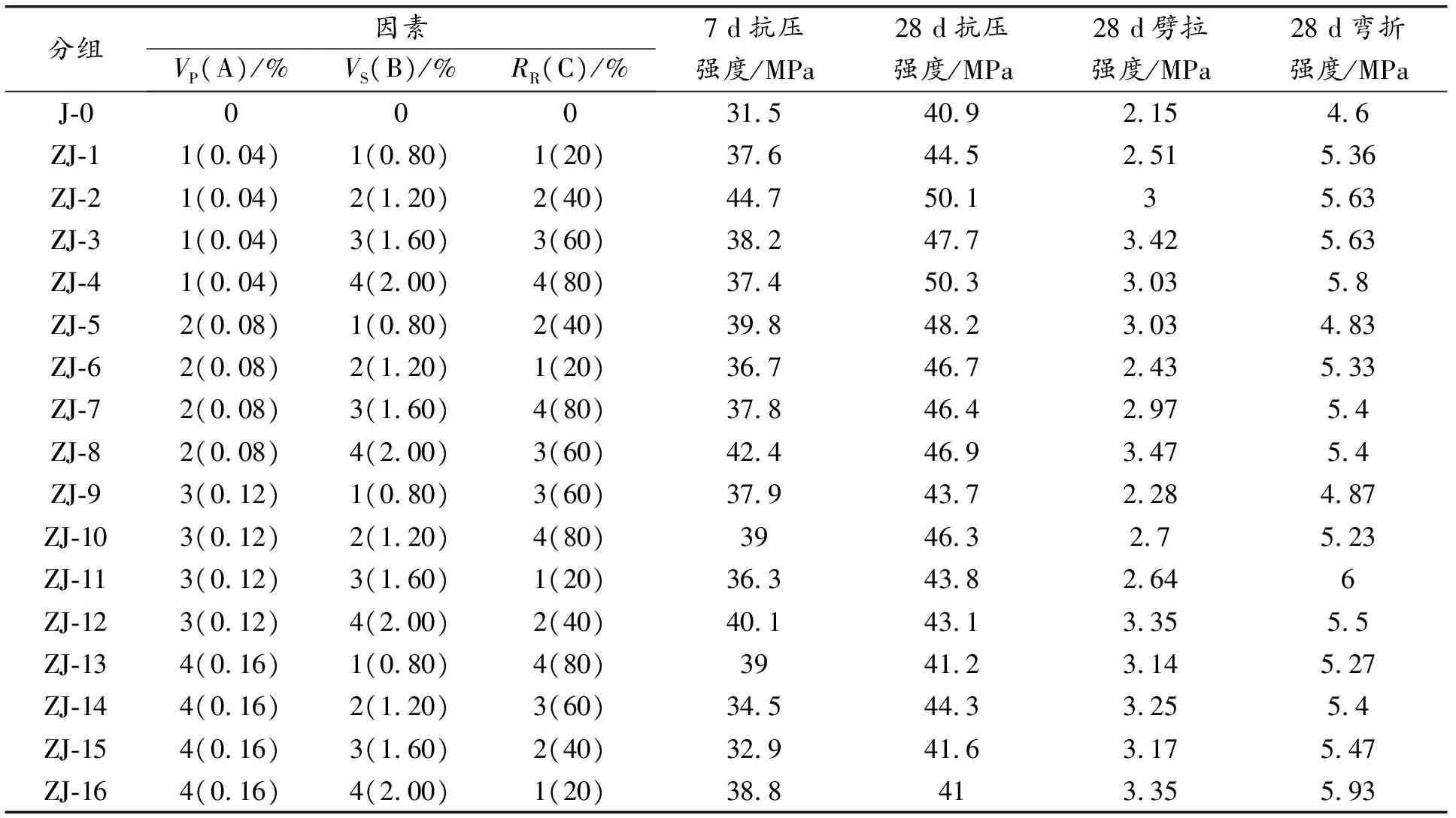
表5 J-0和ZJ-(1～16)正交试验结果

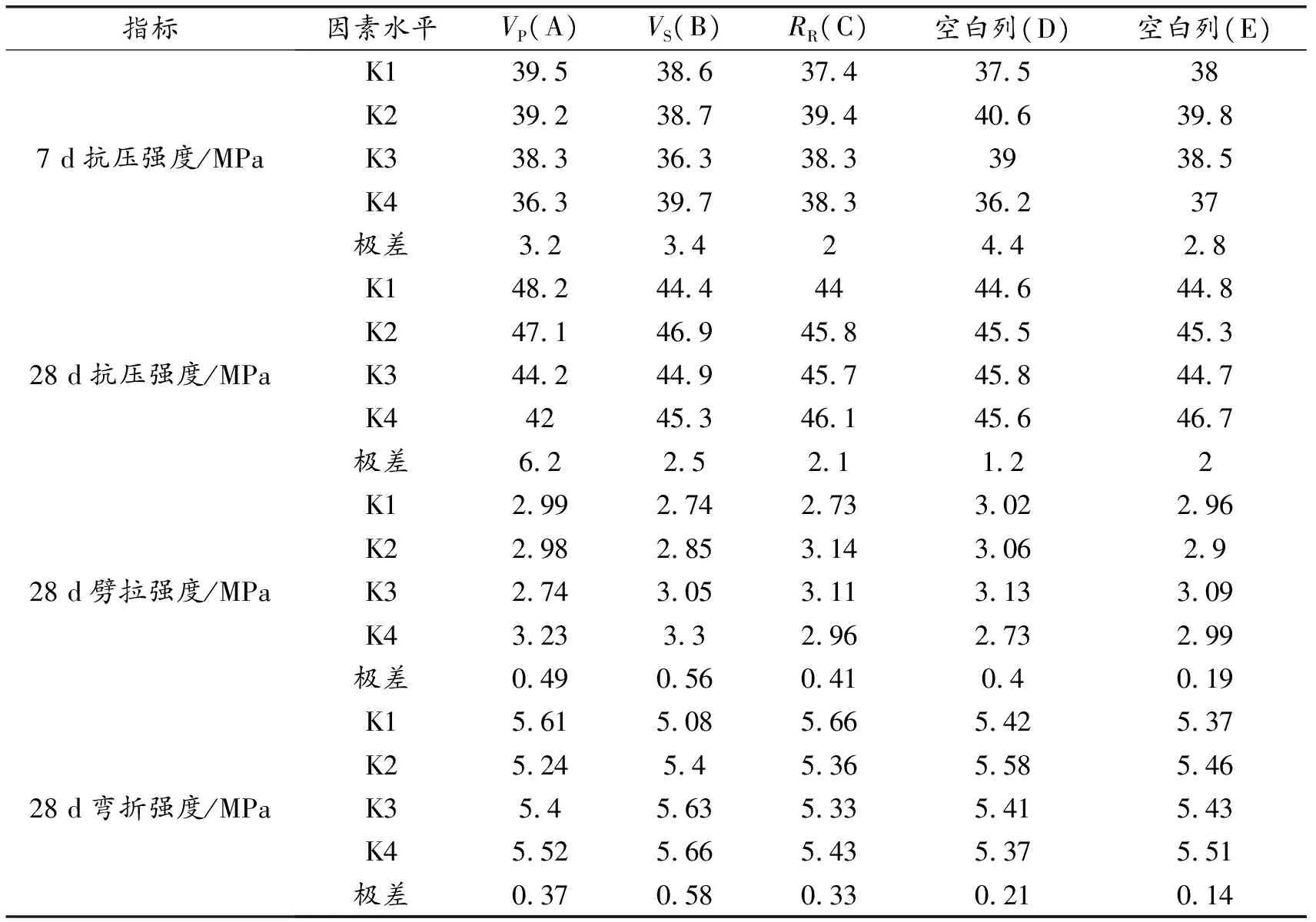
表6 极差分析

2.3 试验数据分析

2.3.1 抗压强度

从表6可以看出，三因素对PP-SF/RCA混凝土28 d抗压强度的影响次序为：VP(6.2 MPa)>VS(2.5 MPa)>RR(2.1 MPa)。表7中三因素对PP-SF/RCA混凝土7 d抗压强度的影响均不显著；VP和RR对于28 d抗压强度影响特别显著，VS有一定影响。

表7 方差分析

在图5(a)和(b)中，除在B2和B3两点强度变化趋势不同，整体上PP-SF/RCA混凝土在7和28 d龄期时的抗压强度随VP、VS和RR的变化趋势相同。由图5(b)可知，随着VP的增加，PP-SF/RCA混凝土28 d抗压强度呈现持续降低的变化趋势，变化范围为13%。当纤维的掺量超过一定水平后，弹性模量较小的PP易相互重叠而相互干扰，在混凝土内部出现结团现象，使纤维与基体的接触表面积减少，降低纤维的有效利用率，在宏观上表现为增强作用减小[13-14]。VS对PP-SF/RCA混凝土28 d抗压强度改善不大，强度随掺量的增加呈现先上升后下降的过程，变化区间在6%之内。过高掺量的SF不利于其在混凝土中充分分散，也会使混凝土不易振捣密实，内部出现空隙，致使强度降低。VP和VS过高的掺量也会导致PP-SF/RCA混凝土出现负混杂效应，从而导致强度下降。

图5 三因素对混凝土7 d抗压强度(a)和28 d抗压(b)、劈拉(c)及弯折强度(d)的影响

在图5(b)中，随着RR的增加，PP-SF/RCA混凝土28 d抗压强度呈现先增加后趋于平稳的变化趋势，变化范围为5%。在搅拌再生混凝土的过程中RCA存在高吸水现象，使混凝土的实际水胶比降低，抗压强度得到增强[15]。随着RR的增加，再生骨料品质劣势的缺陷逐渐暴露出来，使得强度增长随掺量的增加而逐渐放缓。

2.3.2 劈拉强度

从表6可以看出，三因素对PP-SF/RCA混凝土劈拉强度的影响次序为：VS(0.56 MPa)>VP(0.49 MPa)>RR(0.41 MPa)。表7中因素VS对PP-SF/RCA混凝土劈拉强度影响显著，VP和RR有一定影响。

从图5(c)可以看出，VP掺量从0.8%增至2.0%，劈拉强度持续增加了20%；VP掺量从0.04%增至0.16%，劈拉强度先降低后增加，整体上呈现强度增加了8%。高弹模的SF主要依靠其自身与基体间的粘结力和机械咬合力来发挥桥接作用。当混凝土承受荷载作用而产生较小微裂缝时，此阶段PP-SF/RCA混凝土的应力主要由弹性模量较大的SF承担；随着承受荷载的增多，裂缝逐渐扩大，SF承受的应力也随之增多，与此同时，低弹模的PP在发生大的变形后开始发挥增韧作用；PP-SF/RCA混凝土劈拉强度的显著提高体现了PP-SF混杂的良好增强效应，不同性质的PP和SF混杂掺入混凝土中可使纤维在混凝土承受荷载时逐级阻裂，从而增强混凝土的强度。

RR对劈拉强度的影响呈现先先增加后减少的趋势，变化范围为15%。RR<40%时，再生骨料的高吸水现象使得PP-SF/RCA混凝土劈拉强度增大；当RR超过40%后，再生骨料品质劣势造成的劈拉强度下降开始大于实际水胶比降低带来的劈拉强度增长，使得劈拉强度逐步开始下降。

若仅考虑劈拉强度，最佳配合比为：0.16%的VP、2.0%的VS、40%的RR。

2.3.3 弯折强度

23例患者中男10例，女13例；年龄12 ～ 47岁，平均25.6岁；特发性脊柱侧后凸畸形9例，先天性脊柱侧后凸畸形14例，侧凸及后凸顶椎均位于同一节段。侧凸Cobb角均＞ 80°，bending位矫正率均＜ 25%且/或后凸Cobb角＞ 60°［3］。

从表6可以看出，三因素对PP-SF/RCA混凝土弯折强度的影响次序为：VS(0.58 MPa)>VP(0.37 MPa)>RR(0.33 MPa)。表7中因素VS和RR对PP-SF/RCA混凝土弯折强度影响显著，VP没有影响。

VP和VS对弯折强度的影响和劈拉强度呈现相同的变化趋势，整体上呈现强度变化了-2%和11%。随着RR的增加，PP-SF/RCA混凝土弯折强度呈现先减小后增加的变化趋势。RR从20%增至80%分别降低了5%、6%和4%。

若仅考虑弯折强度，最佳配合比为：0.04%的VP、2.0%的VS、20%的RR。

2.4 功效系数法分析

功效系数法可对多个目标问题进行综合评价。从2.3试验数据分析可知，VS、VP和RR对PP-SF/RCA混凝土抗压、劈拉和弯折强度的影响程度不同，无法确定PP-SF/RCA混凝土的最佳配合比，故引入功效系数法。将表5中28 d抗压、劈拉和弯折强度的最大和最小值作为功效系数法评价体系的满意和不满意值[16]，列于表8。

表8 满意值和不满意值

功效系数值计算公式见公式(1)：

(1)

式中：d1、d2和d3分别代表28 d抗压、劈拉和弯折强度的功效系数值。

将表5数据代入公式(1)，得到的功效系数值计算结果见表9。由表9可知，ZJ-4的∑di最大，为281.59。因而综合考虑抗压、劈拉和弯折强度3个指标，建议最佳配合比为：0.04%的VP、2.0%的VS、80%的RR。

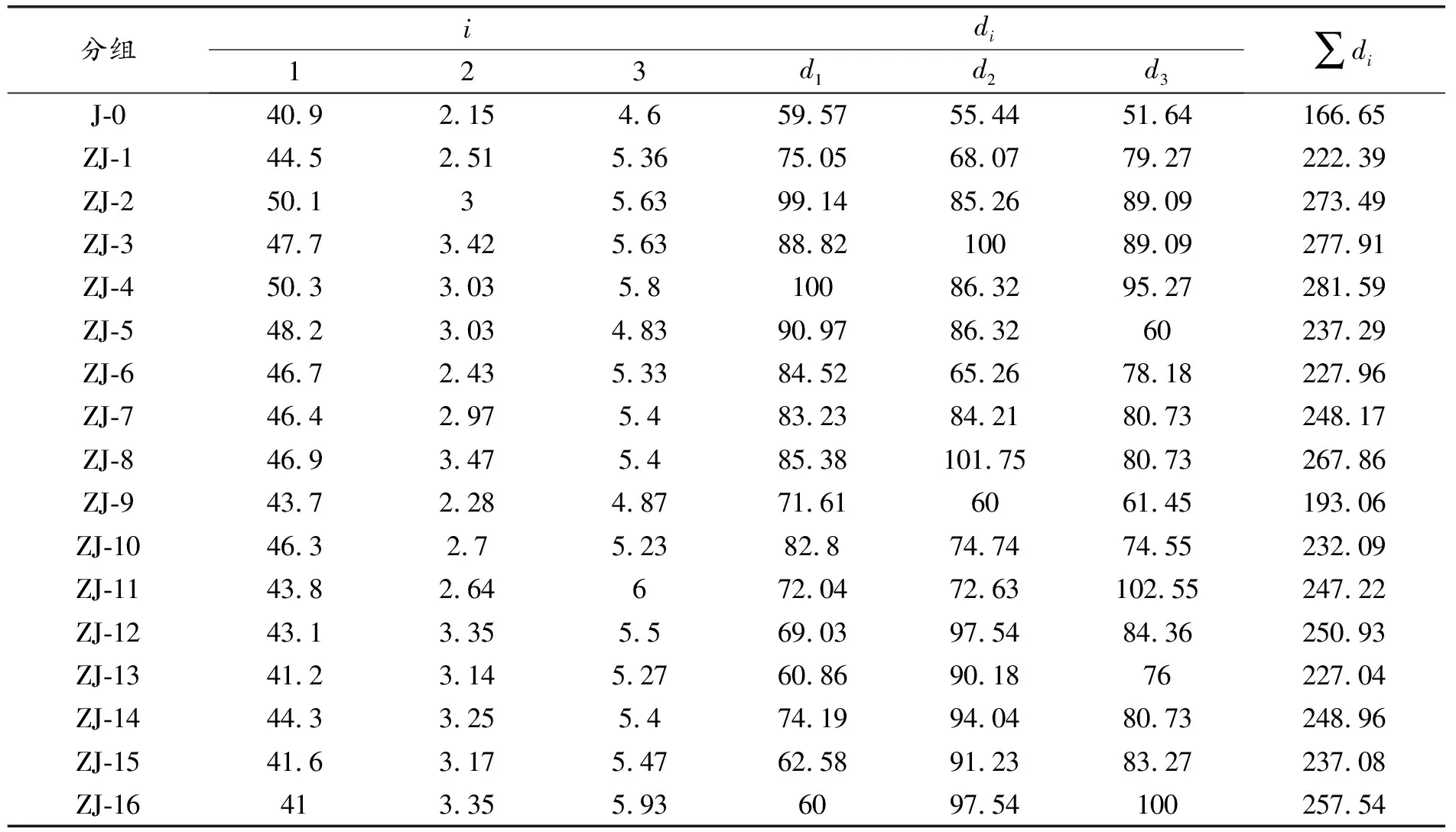
表9 功效系数值计算结果

3 PP-SF/RCA混凝土强度预测模型

引用复合材料力学理论[17]，假设PP-SF/RCA混凝土的强度由基体强度、PP增强项、BF增强项和RCA增强项共同组成。假定强度预测模型见公式(2)：

f=α0+α1x1+α2x2+α3x3+φ

(2)

式中：f为混凝土强度；α0为基体强度；α1、α2、α3为回归系数；x1、x2、x3分别代表VP、VS和RR；为试验参数。

将表5数据代入预测模型公式(2)中，通过最小二乘法估计，得出PP-SF/RCA混凝土的28 d抗压、劈拉和弯折强度的预测模型见公式(3)、(4)和(5)：

fcu=44.36522-4217.11957x1+171.60326x2+5.19076x3(R2=0.5981)

(3)

fts=2.10283+105.25815x1+45.06114x2+0.29552x3(R2=0.5501)

(4)

ff=4.75804+23.76359x1+55.7269x2-0.26247x3(R2=0.6656)

(5)

式中：fcu、fts和ff分别代表28 d抗压、劈拉及弯折强度；R2为决定系数。

从公式(3)、(4)和(5)可以看出，3个公式的决定系数均较低，为0.6左右，离散性较大。图6为根据公式(3)、(4)和(5)进行强度预测得到的PP-SF/RCA混凝土力学性能预测值与实测值的对比图。从图3可以看出，28 d抗压强度在J-0、ZJ-2、ZJ-5和ZJ-6的相对误差较大，均大于±5.5%；28 d劈拉强度在ZJ-3、ZJ-5、ZJ-6、ZJ-9、ZJ-10和ZJ-11的相对误差较大，均大于±11.1%；28 d弯折强度在ZJ-2、ZJ-5、ZJ-8、ZJ-11和ZJ-12的相对误差较大，均大于±5.3%。预测结果与实际值相对误差较大，表明模型精度较低，据推测可能与纤维混杂效应有关[18]。

图6 PP-SF/RCA混凝土力学性能预测值与实测值对比

为精确的预测混凝土的强度，基于纤维混杂效应理论[18]定义新的强度预测模型见公式(6)：

(6)

式中：α4、α5为回归系数。

得出PP-SF/RCA混凝土的28 d抗压、劈拉和弯折强度的新预测模型见公式(7)、(8)和(9)：

(7)

(8)

(9)

根据公式(7)、(8)和(9)得到的新的PP-SF/RCA混凝土力学性能预测值与实测值的对比如图7所示。从图7可以看出，实测值和预测值吻合较好，表明新建立的强度模型精度较高。

图7 PP-SF/RCA混凝土力学性能新预测值与实测值对比

4 结 论

(1)PP-SF/RCA混凝土的7 d抗压强度、28 d抗压、劈拉及弯折强度均大于基准组,较基准组最大增幅分别为41.9%、23.0%、59.1%和28.9%。

(2)7和28 d抗压强度随VP、VS和RR的变化趋势相似，但7 d抗压强度的方差分析结果不显著，据推测原因为7 d龄期时混凝土水化反应不完全，此时混凝土内部各成分之间连接不紧密。

(3)对于28 d抗压强度，VP和RR为特别显著因素，若仅考虑抗压强度，最佳配合比为：0.04%的VP、1.2%的VS、80%的RR；对于28 d劈拉强度，VS为显著因素，若仅考虑劈拉强度，最佳配合比为：0.16%的VP、2.0%的VS、40%的RR；对于28 d弯折强度，VS和RR为显著因素，若仅考虑弯折强度，最佳配合比为：0.04%的VP、2.0%的VS、20%的RR。

(4)采用功效系数法对28 d抗压、劈拉及弯折强度试验结果进行综合评价，建议最佳配合比为0.04%的VP、2.0%的VS、80%的RR。

(5)引用纤维混杂效应理论建立的28 d抗压、劈拉及弯折强度预测模型精度较高。