基于ADAMS的滑块连杆固定型机构动力学仿真分析*

马浩浩，冯彦伟，姚宝珍

(天水师范学院，甘肃 天水 741001)

0 引 言

对机构运动分析在机械设计中具有重要意义，无论开发新机械，还是了解现有机械的动力学性能都是十分重要的。机构的运动分析主要内容是在根据已知的结构参数及原动件的运动规律求解该机构的某些构件上点的位移、速度、加速度、运行轨迹和构件的角位移、角速度、角加速度及工作过程受力分析、做功、能量转化等。平面机构的运动分析主流方法有图解法和解析法，在求解中往往多种方法并行求解，通过对结果分析，绘制运动图线，以更好的解决工程实际问题[1]。笔者选择几种滑块连杆固定型平面四杆机构，分别采用图解法与解析法对机构运动分析，并借助ADAMS软件机构动力学仿真分析，通过分析计算、结果对比，以更加灵活的掌握平面机构运动分析的方法，更好的指导机构创新与应用，具有较高的实践指导意义。

1 滑块连杆固定型平面四杆机构分析

平面连杆在工程应用中应用广泛，如工业机器人、机器臂、机械手、各类展开机构、折叠机构及仿生关节等中均有应用，其中平面四杆机构结构最为简单，加工制造容易、工作使用可靠[2]。

文中在选定两种特殊平面四杆机构加以分析研究，均为滑块连杆固定型机构，运动简图分别如图1中(a)、(b)所示。机构原动件数为1，活动构件数为3，低副数为4，髙副数为0，故机构的自由度为：

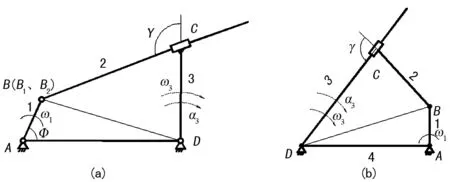
图1 滑块连杆固定型机构运动简图

F=3n-2Pl-Ph=3×3-2×4=1

故该机构具有确定的运动。图1(a)较为常见，图1(b)为图1(a)机构的结构模仿与创新，其具有类似求解方法，后续均以图1(b)为研究对象加以运动分析和动力学仿真。

2 解析法作机构运动分析

选用复数矢量法解析机构的运动特性，通过建立机构的位置方程，再对时间求导分别作机构的速度、加速度分析[3]。

2.1 建立位置方程

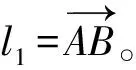
图2 封闭矢量多边形

原动件1的运动规律和各杆的长度已知，即确定l1、l2、l4、θ1的参数，θ4=0，θ3=θ2+γ，l3为变量，s3=l3。由此建立构件的封闭矢量方程为：

l1+l2+s3+l4=0

(1)

2.2 复数矢量法求解

采用复数矢量形式表示构件的封闭矢量方程为：

l1eiθ1+l2eiθ2+s3eiθ3+l4=0

(2)

应用欧拉公式eiθ=cosθ+isinθ分离方程式(2)的实部和虚部，得：

l2cosθ2+s3cosθ3=-l1cosθ1-l4

(3)

l2sinθ2+s3sinθ3=-l1sinθ1

(4)

求解式(4)，可得：

s3=-(l1sinθ1+l2sinθ2)/sinθ3

(5)

将θ3=θ2+γ代入式(3)，可以整理并简化为：

Asinθ2+Bcosθ2+C=0

式中：A、B=(l1、l2、l4、θ1、γ)T，C=-l2sinγ

可以解得：

在求得θ2后，由θ3=θ2+γ可求出θ3，代入式(5)可求s3。

速度分析时将式(2)对时间t求导，可得：

(6)

加速度分析时将式(6)对时间t求导，可得：

(7)

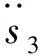
3 ADAMS动力学仿真

用解析法求解机构的运动分析的核心是位置方程的建立与求解，再进一步求导可进行速度和加速度分析，计算中涉及求解非线性方程组及线性方程组的问题，难度较大。文中再选用动力学分析软件ADAMS对该机构做运动仿真分析[4]。

3.1 机构模型构建

建立图1.1(b)所示的滑块连杆固定型机构运动，选取机构参数为：连杆AB长240 mm，AD长780 mm，CD长480 mm，γ=100°，设定原动件1的角速度为30(°)/s，延逆时针回转。

在ADAMS动力学仿真软件中构建机构运动模型，共4个构件，4个关键点，构件的材料类型默认为steel，密度：7.801E-06 kg/mm3。为方便求解杆3的运动参数，选D点为坐标0点，机构关键点初始坐标值如表1所列。

表1 机构关键点初始坐标值

杆4为机架，即AD固定；杆1为原动件，转动中心为A点；滑块与连杆固定的杆2绕B点转动，滑块沿杆3移动；杆3的转动中心为D点。由此建立该机构的虚拟样机如图3所示。

图3 滑块连杆固定型机构虚拟样机

3.2 模型求解和数据后处理

原动件杆1添加旋转驱动，定义数值为30.0d*time。设定终止时间12 s，回转一个周期，步数600。仿真出杆3的运动规律，一个周期内杆3角速度变化曲线如图4所示，角加速度变化曲线如图5所示。

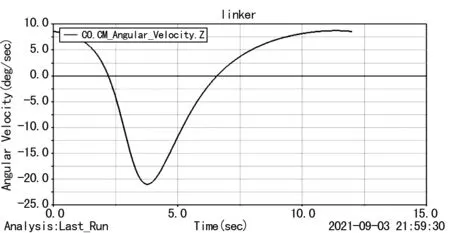
图4 杆3角速度变化曲线

图5 杆3角加速度变化曲线

在解析法求解机构的运动分析时，θ1为原动机杆1对应的方位角，θ3=θ2+γ，对于杆2的方位角θ2也可通过软件仿真求解。由于B点为动点，在求解方位角θ2时采用反转法，构件一经过B点的水平构件，使其与杆1铰链连接与B点处，附加-ω1即可方便求解方位角θ2的数据，变化曲线如图6所示。

图6 杆2方位角θ2的变化曲线

由θ3=θ2+γ，本算例中γ=100°，可求解出杆3的方位角θ3的变化曲线。同时，方位角也可以按照θ3=∠ADC+180°计算。如图7所示，与图6中所示的杆2方位角θ2的变化曲线相差γ值，经验证该机构运动仿真正确，解析法求解计算合理。

图7 杆3方位角θ3的变化曲线

通过动力学仿真求解杆1与机架的连接铰链处(A点)的反力，如图8所示，(a)为驱动件杆1铰链作用反力X方向分量，(b)为驱动件杆1铰链作用反力Y分量。

图8 驱动件杆1铰链作用反力的变化曲线

摇杆3铰链作用反力X方向分量变化曲线如图9(a)所示，Y方向分量变化曲线如图9(b)。

图9 摇杆3铰链作用反力的变化曲线

4 结 语

针对滑块连杆固定型平面四杆机构分析研究，通过解析法与应用ADAMS多体动力学仿真分别作了滑块连杆固定型平面四杆机构的运动分析。用解析法求解机构的运动分析计算中涉及求解非线性方程组及线性方程组的问题，难度较大；应用ADAMS多体动力学仿真软件对机构各构件的角速度、角加速度、铰链反作用力等数值计算[5]，对复合矢量法求解中的方位角也加以分析，对机构的急回特性加以研究，数值精准。对比结果表明：机构运动仿真求解计算合理，为机构分析提供求解分析方法，为后续机构设计改进、机构应用、产品开发提供有力数据支撑。