俯仰角对一维干涉仪测向及定位的影响分析
2022-01-14赵贵
赵贵
南京科瑞达电子装备有限责任公司(原924厂) 江苏 南京 211100
1 干涉仪测向原理
干涉仪测向系统中干涉仪测向阵通常由多个天线单元组成,每两个天线单元组合形成多级基线,如下图中天线1分别和天线2、3、4组成了短(d1)、中(d2)、长(d3)三条基线,每个天线单元后面都接着对应的微波通道以及数据采集通道。
根据干涉仪测向系统原理图1可知:

图1 干涉仪测向系统原理图

辐射源目标入射波到达同一基线的两个天线单元时的相位差 由干涉仪基线长度、入射波相对于基线法线的角度、信号波长 共同确定。通过鉴相器解算出相位差 后,即可解算出入射波相对基线法线的角度,如下所示:
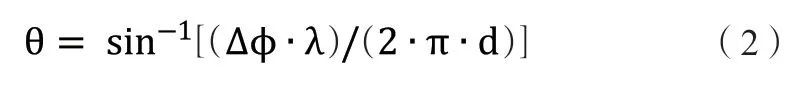
2 建立干涉仪三维测向模型

图2 干涉仪三维测向模型
现做如下假设[1]:
①干涉仪基线d与飞机机身轴线平行安装,图中红线代表干涉仪基线d;②H为载机相对于目标的垂直高度;③R为飞机在目标所在水平面上投影与目标之间距离;④为干涉仪基线在目标所在水平面投影与目标之间夹角(水平方位角);⑤ 为测量得到的干涉仪基线与目标之间夹角(立体方位角);⑥为入射电磁波相对于干涉仪基线法线的夹角;⑦为载机相对于目标所在水平面的俯仰角,即载机与目标连线与目标所在水平面之间夹角;
根据直角三角形中边、角关系可知:

进行等价变换即可用三维立体方位角w与载机相对于目标所在平面的俯仰角表示:

3 一维干涉仪测角误差分析
下面就一维干涉仪测向系统中立体方位角 和平面方位角进行对比分析。
假设载机与目标之间俯仰角分别为4°、5°、6°、7°、8°、9°、10°,入射波与基线法线的夹角 由-90°变到90°时立体方位角 和平面方位角 之间差值曲线如图3所示:

图3 测角差值随目标方位角变化
从图中可发现,当入射波垂直基线法线附近入射(即目标方位角为90°)时,测角差值 相差最小,测角差值 随着入射波与基线法线之间夹角的增加而增大[2]。干涉仪系统测向方位区间通常在法线 范围,固定= 60°,俯仰角 由0°变化到10°,观察图4可知,测角差值随着俯仰角增加而增加,在俯仰角为10°时,测角差值达到最大值1.6度左右,若俯仰角继续增加,则测角差值将进一步增大[3]。
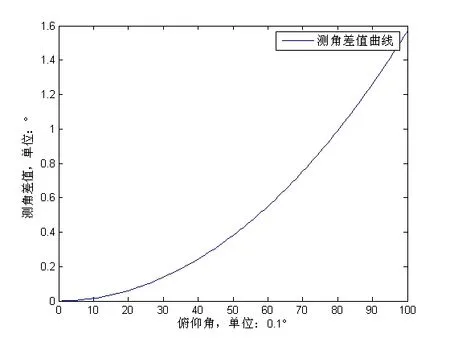
图4 测角差值随俯仰角变化
4 测角误差对测向交叉定位的影响分析
实验2:假设飞机飞行速度为100m/s,飞机飞行高度10000m,飞机相对于目标起始距离为50Km,起始方位角为45°,测角均方根误差为1°。
当采用立体方位角w与平面方位角 分别进行测向交叉定位时,进行300次蒙特卡洛实验得定位误差收敛对比曲线如下:
从图5(a)和图5(b)可看出,这时采用立体方位角进行测角交叉定位比利用平面方位角得到的定位误差要大2%~3%。

图5 定位误差收敛对比曲线
从上表2中可知,在俯仰角大到一定程度(11.5°)后,采用不同的方位角进行定位得到的定位精度和收敛速度具有较大区别。

表2 利用不同方位角时测角交叉定位收敛速度与收敛误差对比
5 结束语
由本文分析可知,一维干涉仪无源测向系统在载机与目标之间的俯仰角固定情况下,目标入射波来波方向与干涉仪基线法线之间夹角越大,测角误差越大;目标入射波来波方向固定情况下,载机与目标之间俯仰角越大,测角误差越大[4]。同时载机与目标之间的俯仰角、目标入射波来波方向与干涉仪基线法线之间夹角增加也会导致测角交叉定位的误差增大、收敛速度变慢。
根据一维干涉仪无源测向系统的测向误差分析可知,在实际工程中应用一维干涉仪测向、定位时,应尽可能使得目标入射波来波方向接近干涉仪基线法线方位,同时应尽可能降低载机与目标之间的俯仰角(降低载机飞行高度、拉开与目标距离)。
