MPSR-MKSVM电力负荷预测综合优化策略

2022-01-14徐蕙陈平李海涛王瀚秋秦皓陈少坤

电测与仪表 2022年1期

徐蕙，陈平，李海涛，王瀚秋，秦皓，陈少坤

(1.国网北京市电力公司，北京 100031； 2. 北京恒华龙信数据科技有限公司，北京 100088)

0 引言

电力负荷预测对电力系统供应计划的制定以及电力系统运行保障都有着很重要的参考价值，准确的电力负荷预测能够极大地提升电力使用的效率，因此，电力负荷预测研究得到了极大的关注[1-9]。

相空间重构与支持向量机由于其各自的优点在预测领域得到了广泛应用，文献[10]利用CAO方法求得相空间重构参数，然后利用粒子群算法优化的支持向量回归对电力负荷进行了预测，结果证明了该方法具有一定的预测精度。文献[11]通过基于C-C方法与遗传算法优化的相空间重构LS-SVM对网络时延进行了预测，结果证明了该方法具有较好的精度与实时性。上述文章均是将相空间重构与支持向量机的参数独立进行选择，此种方式存在一定的保守性，无法使得参数达到预测最优。针对这一问题，文献[12]用粒子群算法对相空间重构参数与SVM参数进行联合寻优，得到交通流量预测模型以及碳市场价格预测模型，结果证明了该联合优化方法的优越性。但是电力系统是一个复杂的动力学系统，很难由一维时间序列通过延迟嵌入法重构出该系统的相空间[13-15]。单一核函数支持向量机预测性能具备一定的局限性，而且电力负荷预测的研究通常为离线预测，对在线预测的研究较少。

为实现在线电力负荷预测，并进一步提升预测精度，结合多变量相空间重构以及组合核函数LS-SVM，提出一种基于混沌自适应人工鱼群算法短期电力负荷滑动时窗在线预测综合优化方法，并验证了提出的方法能够在保证较快预测速度的条件下能够达到较高的预测精度，实现了有效地在线预测。

1 在线预测模型

1.1 多变量相空间重构

电力负荷时间序列具有混沌特性，可依据其混沌特性建立预测模型对电力负荷进行短期预测[16-18]。单变量混沌时间序列是通过单一时间变量对系统进行应用分析，但是在实际应用中，基于单变量时间序列的混沌预测模型不能够完全描述系统的混沌特性，从而使得预测结果不准确[19-20]。而多变量时间序列的引入，有利于恢复原动力系统混沌吸引子全貌，可以更加真实有效地还原电力系统的动力学特性，改善了单一变量相空间重构不完备的缺点[21-23]。

若影响电力负荷大小的因素有D维，其相应的时间序列为{Ai,i=1,2,…,D};其中，Ai=[Ai(1),Ai(2),…,Ai(N)]T，N表示时间序列的长度，τi和mi分别代表第i维时间序列的延迟时间与嵌入维数，从而可以得到D维多变量时间序列的相空间表达式：

(1)

(2)

1.2 组合核函数LS-SVM

存在样本(x1,y1)，(x2,y2)，…，(xi,yi),…，(xl,yl)，其中xi∈Rn表示输入向量，yi∈R表示输出向量，则求解问题可转换为：

(3)

式中φ(·):Rn→Rnh为映射函数；w∈Rnh代表的是权值系数，ei∈R为误差向量，b∈R为偏置系数；γ>0为惩罚因子，其中惩罚因子会对预测精度产生较大影响。

相应的基本方程为：

(4)

相应的回归函数为:

(5)

定义特征矩阵：Q=Ω+γ-1I，其中:

(6)

常规的核函数包括以下三种：

(1)多项式核函数：

Kp(x,y)=[λ(xTy)+c]d

(7)

(2)Sigmoid核函数：

Ks(x,y)=tanh(ηxTy+k2)

(8)

(3)高斯核函数：

(9)

其中，x,y代表输入空间向量；λ,c,d,η,σ为核函数的参数。除此之外还有许多其他种类的核函数，为简化计算量，只通过上述三种核函数组合为新核函数。

根据文献[12]得知核函数满足三条性质，根据该些性质，能够将其进行任意的排列组合从而获得许多不同的核函数，其排列组合过程如图1所示。

(10)

式中Ki表示的是排列组合的新核函数；ωi代表的是各个组合核函数的权值系数。

图1 核函数组合示意图Fig.1 Schematic diagram of kernel function combination

1.3 滑动时窗策略

滑动窗口策略如图2所示，此问题可以转换为如何得到Q的逆矩阵，令QL=ΩL+(1/γ)I，其中QL∈RL×L；ΩL∈RL×L，Ωi,j=K(xi,xj)，i,j=1,2,…,L。具体的滑动窗口示意图见图2。

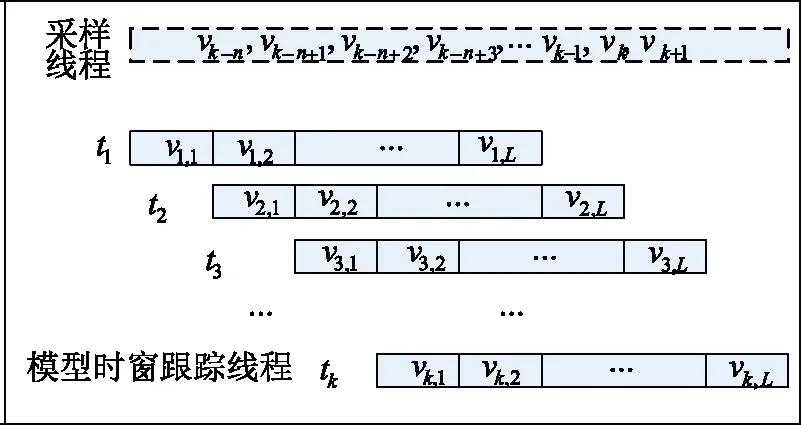
图2 滑动窗口策略示意图Fig.2 Schematic diagram of sliding window strategy

基于滑动窗口多核函数LS-SVM在线预测算法的具体步骤如下：

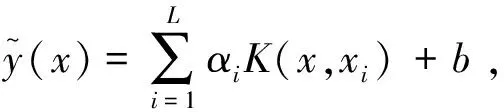
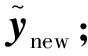
(4)计算出Q′new的值，更新相应的矩阵以及系数；

(7)样本和误差向量进行更新代换，xi=xi+1，yi=yi+1，ei=ei+1,i=1,2,..,L-1；xL=xnew，yL=ynew，eL=enew；

对上述过程进行循环处理，即可实现滑动窗口的在线移动。

2 电力负荷预测同步优化策略

2.1 混沌自适应人工鱼群算法

人工鱼群算法是一种新型群智能优化算法，该算法通过模仿鱼群的觅食、聚群、追尾等主要行为，从而实现优化。但是，基本人工鱼群算法存在诸多弊端,诸如收敛速度慢、易陷入局部最优等，为提升算法的优化效果，有学者提出一种自适应步长与视野的人工鱼群算法[24]。进一步为解决陷入局部最优问题，文中利用文献[25]提出的混沌自适应步长视野的人工鱼群算法对相关参数进行优化。

2.2 优化步骤

定义单个人工鱼为F=(τi,mi,C,δ,λ,c,d,η,δ,w1,w2,…,wn)，该电力负荷预测综合优化可以转换为寻找最优人工鱼Fopt，使得适应度函数Fitness接近0，适应度函数的表达式为：

(11)

(12)

步骤1：确定人工鱼群算法的基本参数，并确定多核函数的组成以及个数；

步骤2：给定(τi,mi,C,δ,λ,c,d,η,δ,w1,w2,…,wn)该向量代表人工鱼群的初始状态；

步骤3：判断是否符合约束条件。若满足，则利用延迟时间τi与嵌入维数mi对多影响因素进行多变量相空间重构;若不满足，则直接跳至步骤5；

步骤4：重构后的向量作为多核支持向量机的输入，根据给定的多核支持向量机的各个参数以及核函数权值对训练样本进行训练预测，求出反映预测精度的适应度函数；

步骤5：人工鱼执行行为得到新的人工鱼状态，人工鱼执行觅食、追尾、聚群以及随机等行为；

步骤6：重复步骤3和步骤4,求出此时人工鱼的适应度函数，并与初始适应度函数进行比较，将较优的人工鱼个体计入公告板;

步骤7：最优人工鱼执行混沌搜索;

步骤8：将混沌搜索得到的人工鱼与公告牌上人工鱼对比，更新适应度值；

步骤9：判断是否满足最大迭代次数。若等于，那么输出最优值；若小于，那么返回步骤5，再进行下一次迭代寻优。

3 预测结果分析

为简化优化参数，令不敏感系数ε=0.01，多项式核函数参数d=3，其它参数满足λ∈[0,3],c∈[0,3],σ∈[0,1]，已知影响电力负荷的因素包括温度、风速、湿度三个因素，所以令变量维数D=3，为减少计算量，相应的子核函数个数n=6，其组成为如表1所示。

令人工鱼数目为NUM=20，最大迭代次数Iterate_times=170，初始化视野Visual=5，拥挤度因子φ=0.5，觅食尝试次数Try_number=5，衰减因子α=0.9，β=0.6，阈值δ=0.2。

表1 核函数组成Tab.1 Composition of kernel functions

文中所有数据均来自于台州市电力局，训练数据为台州市12月7日～12月14日的负荷数据，考虑到休息日与工作日负荷数据差异，利用不同的预测模型分别对工作日12月15日以及休息日12月20日的电力负荷进行在线预测。利用工作日的电力负荷训练数据进行参数优化得到的优化结果如图3与表2所示。

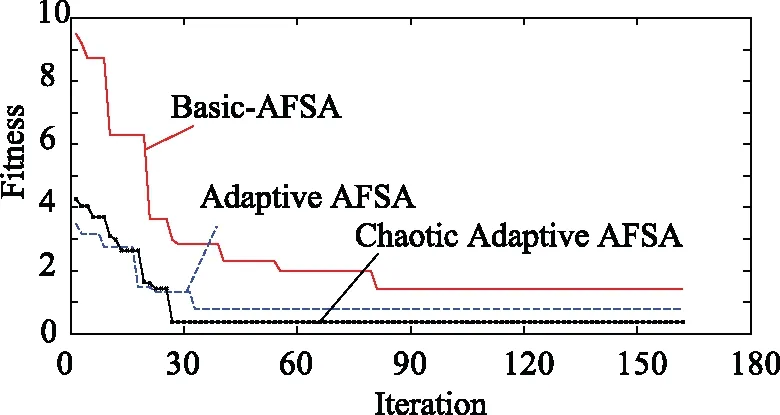
图3 优化对比结果Fig.3 Optimization comparison results

表2 优化对比结果Tab.2 Comparison results of optimization

可以看出混沌人工鱼群算法优化的适应度函数Fitness相对于其他两种优化方法最接近0，说明该种算法的收敛精度更高。另外，其收敛迭代次数为26，较基本人工鱼群与自适应人工鱼群分别减少了58次和8次，证明了该种混沌自适应人工鱼群算法在多参数寻优问题中依旧能够在保证较快的收敛速度以及较高的收敛精度。

权值优化曲线见图4，利用上述优化得到的参数，先对预测数据进行相空间重构，进一步将得到的多变量相空间作为支持向量机的输入参数，从而得到相应的预测模型。分别利用传统PSR-LSSVM参数独立选取、MPSR-LSSVM参数独立选择、MPSR-MKLSSVM参数综合优化以及MPSR-MKLSSVM参数综合优化四种预测方法对工作日12月15日台州市电力负荷进行在线预测，图5与图6为预测结果图以及绝对误差图。从中可以看出MPSR-MKLSSVM联合优化最靠近真实负荷曲线，且绝对误差曲线最接近理想误差线。

图4 核函数权值优化结果Fig.4 Weight optimization results of kernel function

图5 工作日在线预测结果图Fig.5 Online forecasting results of working days

图6 工作日预测误差图Fig.6 Forecast error chart of working days

为更直观地比较各个方法之间的优劣，表3显示了四种方法在不同时间点的预测值与实际值平均绝对误差与平均相对误差，从表3中可以看出，PSR-LSSVM参数独立优化方法的平均相对误差为4.52%，而MPSR-LSSVM独立优化方法与MPSR-MKLSSVM独立优化的平均误差分别减小了1.54%和2.41%，证明了多变量相空间重构能够提升预测精度，多核函数相对于单一核函数来说对预测精度也有提升作用，而且对比MPSR-LSSVM独立优化方法与MPSR-MKLSSVM独立优化方法可知，多核函数在提升预测精度的影响上明显强于多变量重构。另外，MPSR-MKLSSVM联合优化相比于MPSR-MKLSSVM独立优化的平均相对误差减少了0.67%，进一步说明了联合优化相对于独立选择优化，其预测精度更高。

表3 工作日预测误差表Tab.3 Prediction error of working days

再利用上述四种方法对休息日12月20日台州市的电力负荷进行预测，图7和图8为休息日的电力负荷预测结果图以及绝对误差图。可以看出预测结果于工作日类似，MPSR-MKLSSVM联合优化相对于其他优化方法来说最靠近真实负荷曲线，且绝对误差曲线最接近理想误差线。

图7 休息日预测结果图Fig.7 Forecast results of rest days

图8 休息日预测误差图Fig.8 Prediction error chart of rest days

表4 休息日预测误差表Tab.4 Prediction error of rest days

同理，表4显示了四种方法在不同时间点的预测值与实际值平均绝对误差与平均相对误差，从表4中可以看出，PSR-LSSVM参数独立优化方法的平均相对误差为4.99%，而MPSR-LSSVM独立优化方法与MPSR-MKLSSVM独立优化的平均误差分别减小了1.91%和2.55%，同样说明了多变量相空间重构与多核函数对预测精度均有提升作用，而且多核函数在提升预测精度的影响上明显强于多变量重构。另外，MPSR-MKLSSVM联合优化相比于MPSR-MKLSSVM独立优化的平均相对误差减少了1.26%，同样说明了联合优化相对于独立选择优化的预测精度更高。