驱动力作用下的单摆运动研究 ①

孙 进, 丁宗玲

(安徽大学物理与光电工程学院， 安徽 合肥 230039)

0 引 言

单摆是日常生活中以及工程中的常见模型，具有较为广泛的应用，因而一直以来都是学者们关注的对象[1-5]。在本科生大学物理教学中，为了计算的方便，一般将其简化成简谐振动[6]，以便学生对其运动有简单的认知。但实际上，单摆的运动是复杂而多变的，可能是规律运动也可能是随机行为。只有在不考虑阻力及驱动力，且初始摆角非常小的情况下，单摆的运动才能近似归结为简谐振动。在更为普遍的情况下，单摆将做周期与初始摆角相关联的周期振动甚至转动以及出现混沌现象[7-8]。

对于单摆在不同情况下运动状态的分析，有助于学生更加清晰的了解单摆的实际运动的变化。但由于在这一过程较为复杂，甚至会出现混沌的非线性变化，其运动方程很难进行精确的解析求解。作者之前曾采用数值计算的方法求解完整的运动方程，对单摆在有阻力和无阻力情况下的实际运动进行过比较和分析[9]。在这篇文章中，进一步加入对于外界驱动力的考虑，利用计算机对驱动力作用下单摆的运动进行了模拟计算。通过改变不同的参数，展示不同的驱动力对于单摆运动的不同影响，希望能够更加清晰的展示出单摆的运动特征，帮助学生更加透彻地理解单摆的运动。

1 数值计算方法

在周期性驱动力的作用下，单摆的运动方程可以表示为：

(1)

其中m和l分别代表单摆的质量和摆长。在方程(1)中，单摆分别受到重力，与速率成正比的空气阻力以及角频率为ω的周期性驱动力的作用。为了使研究结果更具普遍性，本文对方程(1)不做任何简化，在保证精度的前提下，采用数值方法处理微分方程的初值问题，对其进行求解。在数值计算方法中，Runge-Kutta[10]是一种公认较为精确的方法，它可以用来求解一阶常微分方程组，较为常用的是四阶和六阶Runge-Kutta。在之前对于单摆的研究中[9]，采用四阶Runge-Kutta方法取得了较好的结果，因而这篇文章里沿用此方法解方程(1)，得到不同时间点上单摆运动的角位移θ以及角速度dθ/dt。

2 计算结果

不同的驱动力对单摆会产生不同的影响，改变驱动力的频率和大小，单摆的运动将发生非常有趣的变化。

2.1 驱动力较小时单摆的受迫振动及共振

图1 不同条件下单摆的摆角随时间的变化

保持其它参数不变， 图2(a)展示了单摆稳定后振动的振幅随驱动力的角频率而发生的变化，振幅最大处即为共振。当f=1N时，共振发生在ω=3.05rad/s。图2(a)中嵌入的小图为f=1N时单摆运动的相轨迹，黑色代表ω=2.5 rad/s而红色代表ω=3.05 rad/s。在重力、阻力和驱动力的共同作用下，单摆最后的运动相图都归为闭合的椭圆，也就是稳定的周期运动，当ω=3.05 rad/s时，椭圆的面积明显增大很多，说明在其它条件不变的情况下，共振大大增大了体系的机械能。

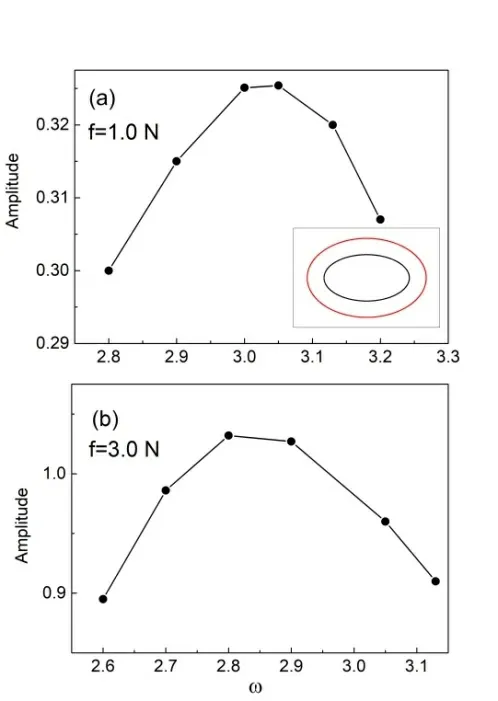
图2 单摆达到稳定运动后振幅随驱动力角频率的的变化

此外，计算结果显示共振对应的驱动力的角频率并不是自由单摆对应的固有角频率3.13 rad/s，而是发生了偏移，出现在ω=3.05 rad/s。对于共振频率偏移的原因可以通过运动方程的解析解来解释。在小摆角的情况下取sinθ≈θ，由简化的方程(1)可以解析解得单摆达到稳定后的振幅为：

2.2 驱动力振幅的影响

随着驱动力的继续增强，单摆的运动将不再趋于稳定。如在γ=2.5，f=20.5 N,ω=2.5 rad/s的情况下，单摆在经历了短暂调整过后，并没有达到单一频率的振动状态，而是在两个不同频率之间来回变化，即为产生了二倍分叉。为了能够更加清晰的看出单摆运动的变化，我们将200s之后单摆运动的相图展示在图3中。由图3(a)可见单摆的相轨迹在交叉的两个闭合图形上变换，对应着在两种稳定的振动状态之间不断变换。随着驱动力的不断增强，单摆振动的频率分叉逐渐增多，如图3(b)-(d)所示，从二倍分叉到四倍再到八倍，最后单摆将不会出现稳定的运动状态，其相轨迹在一片区域里不重复出现，也就是达到了混沌这一非线性状态。

图3 随着驱动力的增大，单摆运动的相轨迹的变化过程

在达到混沌状态以后，继续增大f，单摆的运动还会发生有趣的变化。图4(a)为保持γ=2.5，ω=2.5，当f=25.0 N时，单摆的摆角随时间的变化，嵌入的小图是此时的相轨迹。可见混沌现象已经消失，单摆运动的相轨迹变成了较为复杂的闭合曲线。此时单摆又回到了周期运动，但不再是以竖直方向为振动的中心位置，而是向外力的施力方向偏移。其次，在一个运动周期中，单摆的运动也变得更加复杂，不再是单一的往返摆动，而是在不同的摆角振幅以及振动中心之间切换。继续增大驱动力，当f=35.0 N时，由于驱动力远大于重力及阻力，起到主导作用，由图4(b)可见此时单摆恢复了稳定的单频周期性振动，振动的平衡位置保持在θ>0的固定位置。

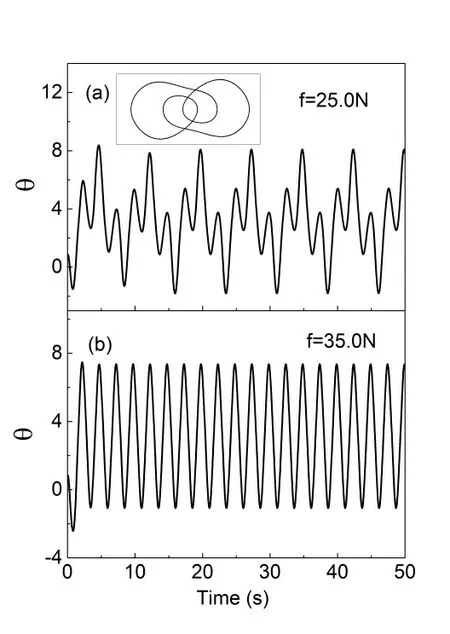
图4 当f分别等于25N和35N时单摆运动的角位移随时间的变化

3 总 结

本文采用四阶Runge-Kutta数值计算方法求解完整的单摆运动方程，对驱动力作用下单摆的运动进行了讨论。首先，在驱动力不是很大的情况下，驱动力的作用会与单摆的摆动相协调，最后形成统一的稳定振动，振动的振幅与驱动力的频率有关。但与一般受迫振动不同的是，单摆发生共振的频率与单摆的本征频率相比会有所减小，驱动力越大，减小得越多。其次，增大驱动力的振幅，会使得单摆最终达到稳定状态的频率发生二倍、四倍、八倍分叉，然后达到非线性的混沌状态。继续增大驱动力，由于驱动力的作用逐渐变成主导，单摆的运动又会恢复到稳定的振动。