八自由度冗余机械臂误差分析 ①

周 冬

(安徽理工大学，安徽 淮南 232000)

0 引 言

为了解决能源问题，人类很早就在尝试核聚变装置，中国从上世纪六十年代开始就一直积极地参与国际合作，经过多年的研究中国研制出了属于自己的核聚变装置——中国聚变工程实验堆CFETR(China Fusion Engineering Test Reactor)。中国科学院合肥物质科学研究院(等离子体物理研究所)在CFETR的研发过程中承担着聚变堆主机关键系统综合研究。[1]对该项目中完整主臂及CFETR多功能重载维护机械臂的设计、加工制造、装配、测试等关键技术进行预研，其中机械臂几何误差的分析是关键一环。

1 工作空间

机械臂的工作空间是其运动学与动力学分析的基础，本文采取的误差分析方法基于机械臂工作空间内的一个特定参考平面，通过正逆运动学计算得出相应的误差值，故工作空间的分析是本文研究的前提。

1.1 D-H参数的建立

以CFETR多功能重载维护机械臂MPD(Multiple Purpose Deployer)为研究对象，重点研究静态误差中几何参数误差对机械臂末端位置点的影响程度，该项目对机械臂末端绝对定位精度的目标范围定为±100mm。图1.1为MPD的模型与连杆坐标系，机械臂有一个移动关节与八个转动关节，本文只针对转动关节进行分析。

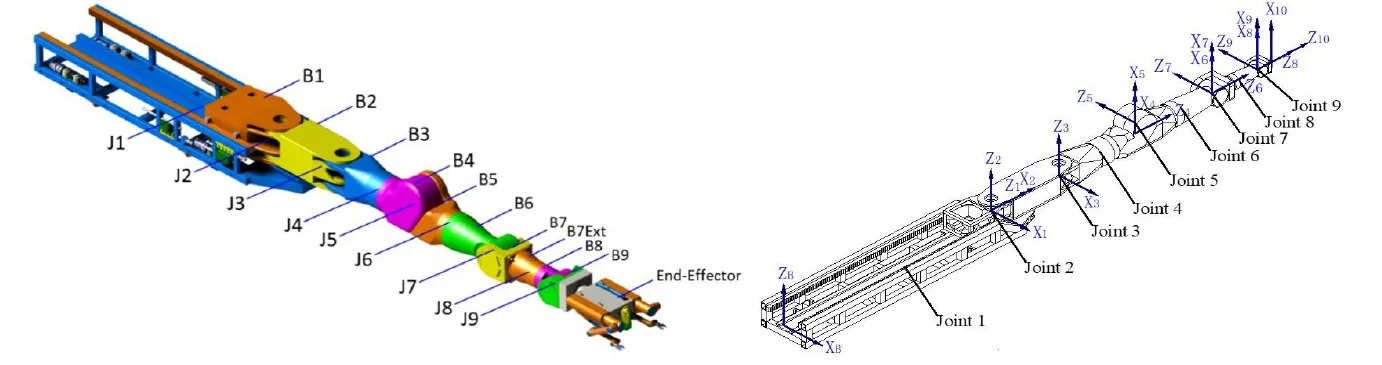
图1 重载机械臂配置

根据D-H法则和机械臂的连接情况，并在忽略移动关节的条件下确定如表1.1所示的D-H参数[2]，其中Alpha代表扭转偏角，a代表杆长，Theta代表关节角，d代表连杆偏置，range代表该关节在实际情况下的可动范围。

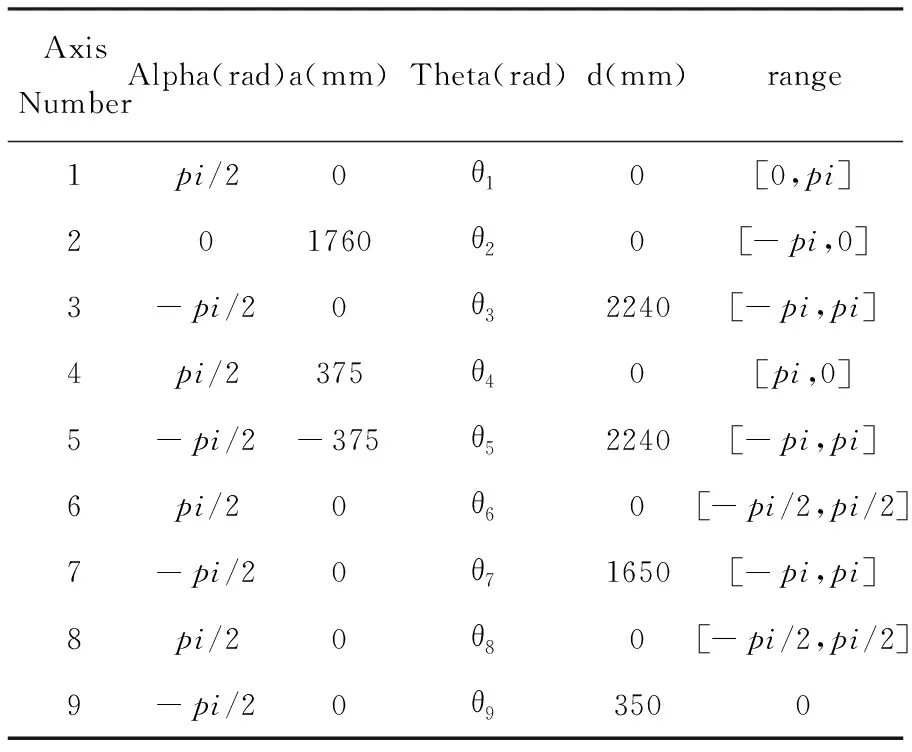
表1 MPD机械臂D-H参数表

1.2 工作空间求解

工作空间的求解方法主要有三种：几何法、解析法、数值法[3-4]。本文选用数值方法对工作空间进行求解，在求解过程中采用蒙特卡洛随机采样的方法，在各个关节的活动范围内随机选取大量的采样点，然后通过MATLAB机器人工具箱编写相关程序得出其正运动学的解，然后在软件中标出相应的末端点位置，从而实现数据的可视化[5]。

图2 重载机械臂工作空间

在MATLAB中得到机械臂的工作空间如图1.2所示，本文选取的平面为机械臂工作空间内垂直于Z轴的平面(设为平面P)，具体参数为x(-100,150)，y(4900,5100)，z(0)。

2 机械臂几何参数误差分析

在机器臂工作过程中，末端的定位精度直接影响着整个工作的进行，影响其精度的因素有很多，其中结构参数误差对末端定位精度的影响程度最大且可通过计算模拟确定，因此有必要在生产制造之前就对其分析，以便为设计加工制造提供指导与参考。

2.1 误差分析方案

机械臂结构参数误差包括关节角零位误差Δθi、杆长偏差Δαi、扭转角误差Δαi、连杆偏距误差Δdi(由于杆长与连杆偏置对末端点的影响较小，因此只针对关节角和扭转角进行分析)。对于这些误差，中将采用给定误差和单关节旋转的方式来对其进行分析[6-7]，根据机械臂设计要求并结合设计经验，给定几何参数设计值与误差值如表2.1所示。

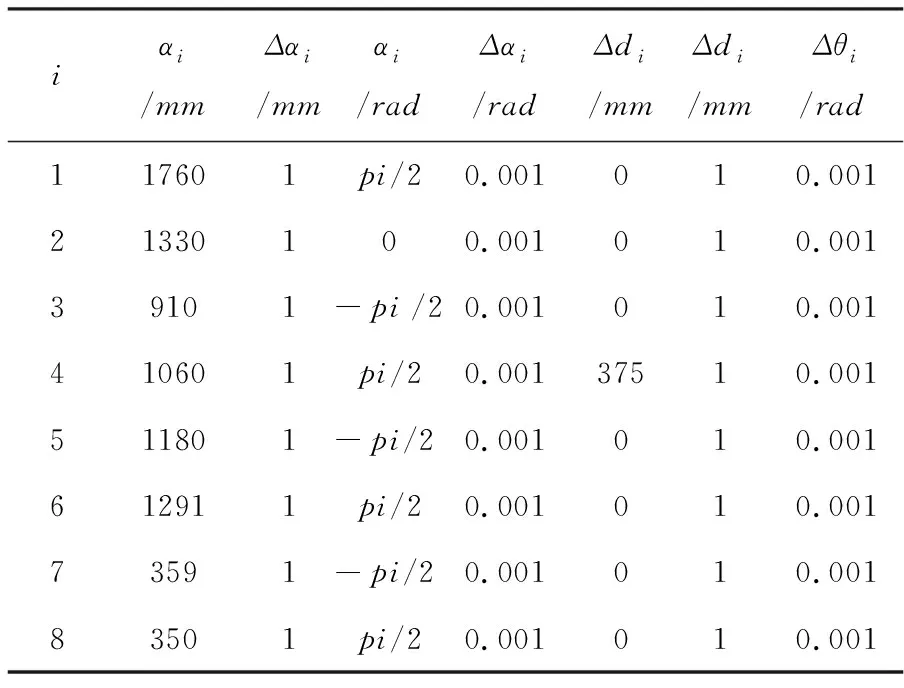
表2 给定机械臂几何参数设计值与误差值

给定误差分析方案如下：在平面P内取一系列参考点视为无误差条件下的位置点，根据机械臂逆运动学计算出一组对应的关节角参数，然后加入某一参数的给定误差值，并根据机械臂正运动学得出在该误差条件下新的位置点，绘制出新旧位置点的曲面图进行比较。

单关节旋转分析方案如下：固定其他关节不动，只研究某一关节的旋转过程(0-360°)，从而计算出该关节的某一结构参数误差对整体机械臂末端位置点的影响程度。选取机械臂的中间姿态(pi/2，-pi/2，0，-pi/2，0，0，0，0)为参考姿态以便于各参数之间的比较。

最后引入参数误差灵敏度K来衡量参数对末端位置波动的影响程度[8]。灵敏度Ki的计算公式为:Ki=Ei/(E1+E2+…Ei-1+Ei+1+…+E8)，式中Ki代表第i个关节某一结构参数的误差灵敏度，Ei代表该结构参数第i个关节的误差均值[9]。

2.2 关节角零位误差

研究关节角零位误差对机械臂精度影响的分析时，将表2中相应的给定误差值分别加到每个关节角上，根据定位误差分析方案，拟合出机器人末端位置所在平面的变化，根据所记录数据，算出的关节角误差引起的末端点整体偏差的均值为6.3996mm。

根据单关节旋转方案，在MATLAB中运用正运动学模拟出机械臂末端点的位置并记录数据点，然后在Origin中根据所记录的数据点绘制出相应的位置曲线如图2.1所示，根据误差灵敏度公式得出的关节角灵敏度如表2.2所示。从图表中可以看出关节3、4影响最大，关节5、7主要控制末端点的位姿变化，对位置的偏移影响较小，灵敏度值相差较大，因此在后期的精度分配中需要根据表2.2中的值对关节角进行更加严谨的设计。

表3 关节角θi存在误差0.001rad下的末端位置误差灵敏度

2.3 扭转角误差

同样根据给定误差分析方案将误差值0.001rad(参考表2.1)分别加到每个扭转角设计值上，然后用MATLAB软件拟合出机器人末端位置所在平面的变化，根据所记录数据，算出的关节角误差引起的末端点整体偏差的均值为1.1368mm。

根据单关节旋转方案，在Origin中根据所记录的数据点绘制出相应的位置曲线如图2.2所示，根据误差灵敏度公式得出的关节角灵敏度如表2.3所示。从图表中可以看出扭转角对末端点位置的影响程度要小于关节角，各扭转角的灵敏度相差不大。

表4 扭转角αi存在误差1mm下的位置误差灵敏度

3 结 语

采取给定误差的方式对机械臂参数误差进行整体分析，然后通过单关节旋转的方式进一步分析每个关节的误差灵敏度；通过MATLAB与Origin软件实现了数据的可视化。由于本文只针对结构参数中的关节角和扭转角进行了分析，下一步分析中将对其他两个参数进行探讨；另外，关节型机械臂的关节间隙也是末端位置误差的一个重要误差源，下一步分析将针对关节间隙进行探讨。

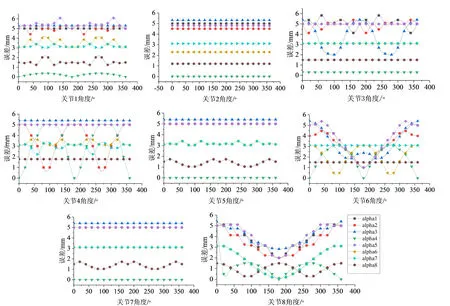
图4 扭转角αi存在0.001rad误差时的位置误差曲线