SARIMA - SVR混合模型在电费收入预测中的应用
2022-01-14孙越洪义成刘鑫张志强郑雪燕
孙越, 洪义成, 刘鑫, 张志强, 郑雪燕
( 1.延边大学 理学院, 吉林 延吉 133002; 2.国网吉林省电力有限公司 延边供电公司, 吉林 延吉 133000 )
电费收入是供电企业运营中的一项重要经济指标.在我国,由于电力商品并不像其他商品采取现场等价交易的方式,而是采用先购买再使用的方式,因此供电企业的电费收入不仅受到用户使用电量的影响,还受到用户缴纳电费全额的影响,即包括了许多随机因素[1-3].目前,预测电费收入的方法主要分为两种方法:一是利用时间序列模型(包括AR模型、ARMA模型、ARIMA模型等)进行预测[4-7],这类模型虽然在操作上方便,但是对数据要求较高;二是利用机器学习方法进行预测,该模型虽然较为复杂,但是在组织和拟合参数方面准确度较高,同时拟合任意非线性趋势的效果较好[8-10].为进一步提高电费收入的预测效果,本文提出一种将时间序列和机器学习相结合的SARIMA - SVR混合模型,并对模型的有效性进行了验证.
1 分析方法
1.1 季节时间序列模型(SARIMA模型)
时间序列模型[11]是从时间序列中找出变量变化的特征、趋势以及发展规律,以此实现对变量的未来变化进行有效预测的模型.按照模型中是否包含季节性成分,ARIMA模型可分为季节模型和非季节模型,其中描述季节性序列的模型又称为季节时间序列模型(seasonal ARIMA model, SARIMA).SARIMA模型中除了用到一般的差分,还用到了季节性差分S,即用S反映一定的周期(T).用t时刻的值减去t-T时刻的值即可得到季节性差分序列.
对于时间序列{Yt}, SARIMA模型的一般表达式为:
(1)
本文将公式(1)记为SARIMA(p,d,q)×(P,D,Q)s模型,其中s为季节周期,p、d和q为非季节阶数,P、D和Q为季节阶数.SARIMA模型的建模流程图如图1所示.
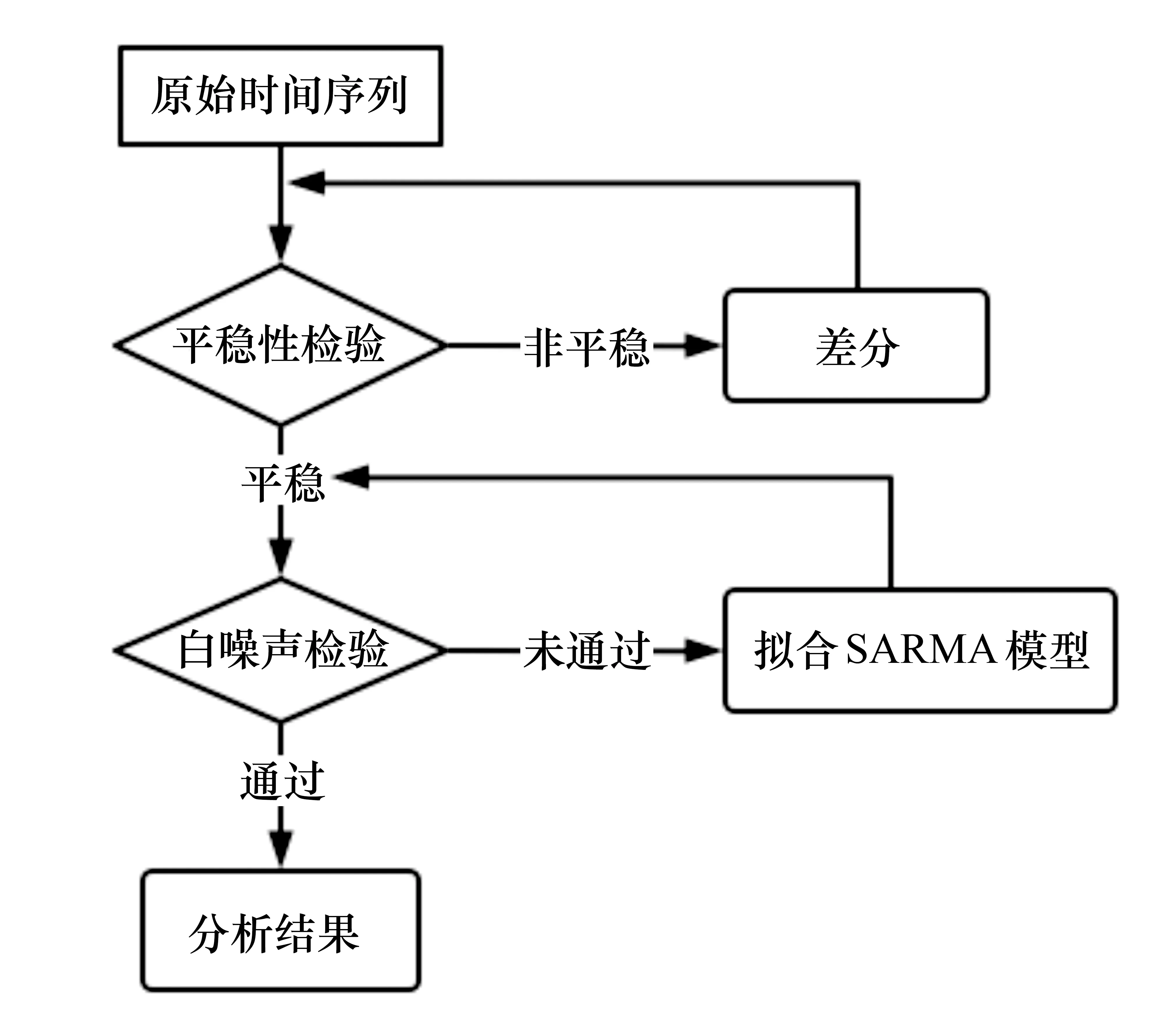
图1 SARIMA模型的建模流程
1.2 支持向量回归模型(SVR模型)
支持向量回归(support vector regression, SVR)模型[12]是在线性函数的两侧建造一个“间隔带”,然后通过最小化“间隔带”的宽度与总损失来优化模型,其中损失函数仅计算间隔带之外的样本.SVR模型利用非线性函数φ(x)将给定的原始数据D={(x1,y1),(x2,y2),…,(xm,ym)}映射到高维空间,以此形成高维空间的线性函数,其表达式为:
f(x)=wT(x)+b,
(2)
其中w为权重,b为截距.假设SVR模型允许f(x)与y之间的最多误差为ε,且仅当f(x)与y之间的差的绝对值大于ε时才计算损失.根据结构风险最小化原则可知, 求解f(x)等效于求解优化问题,即:
(3)

(4)
将回归问题转换为求解目标函数的最小化问题时, SVR模型引入了拉格朗日乘法算子,由此回归问题转换为较为易解的拉格朗日函数:
(5)
利用对偶原理可得式(5)的对偶问题为:
(6)
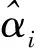
(7)
式(7)中的x可以利用核函数将其表示为φ(xi),从而SVR模型的最终表达式为:
(8)
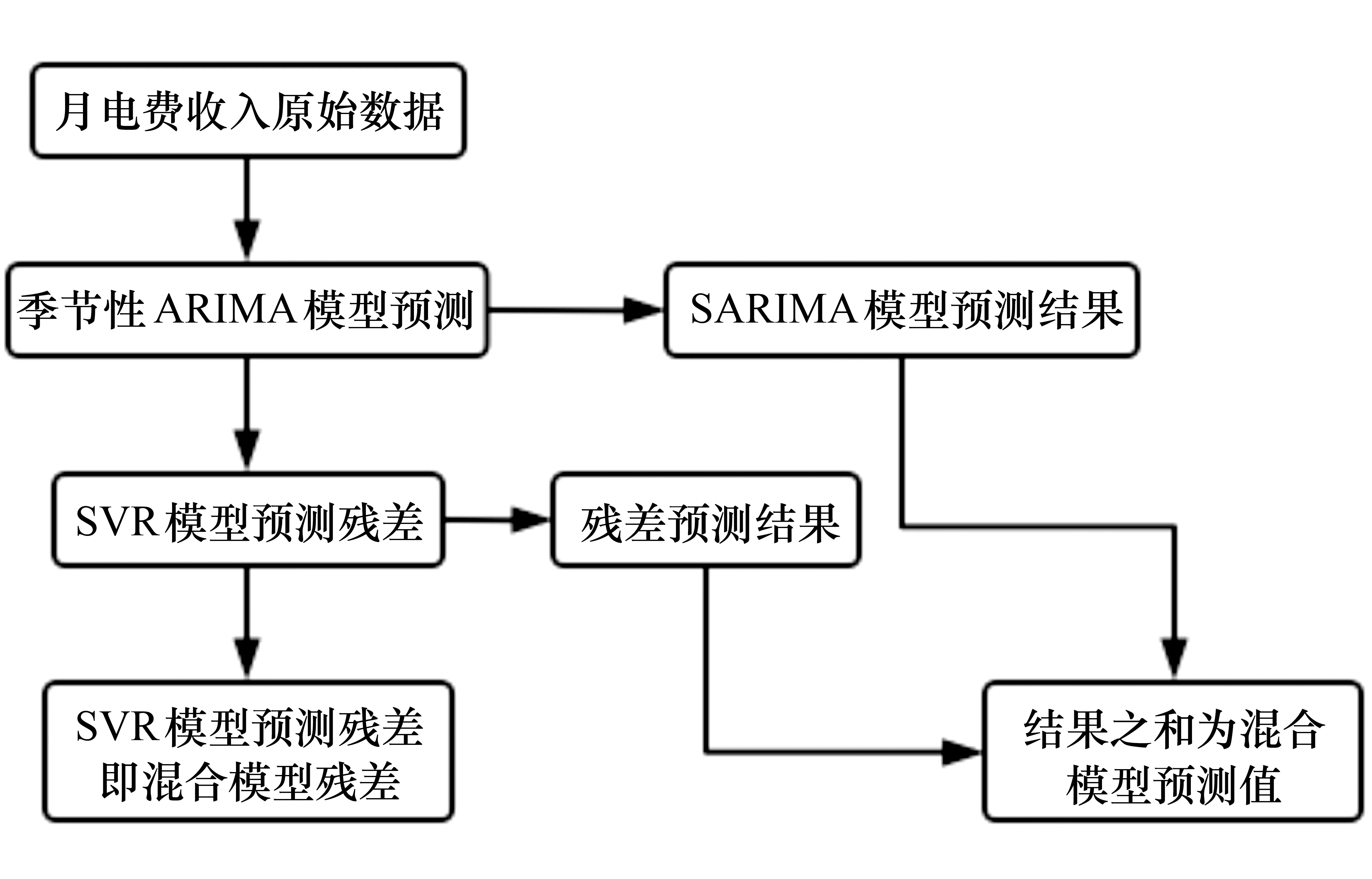
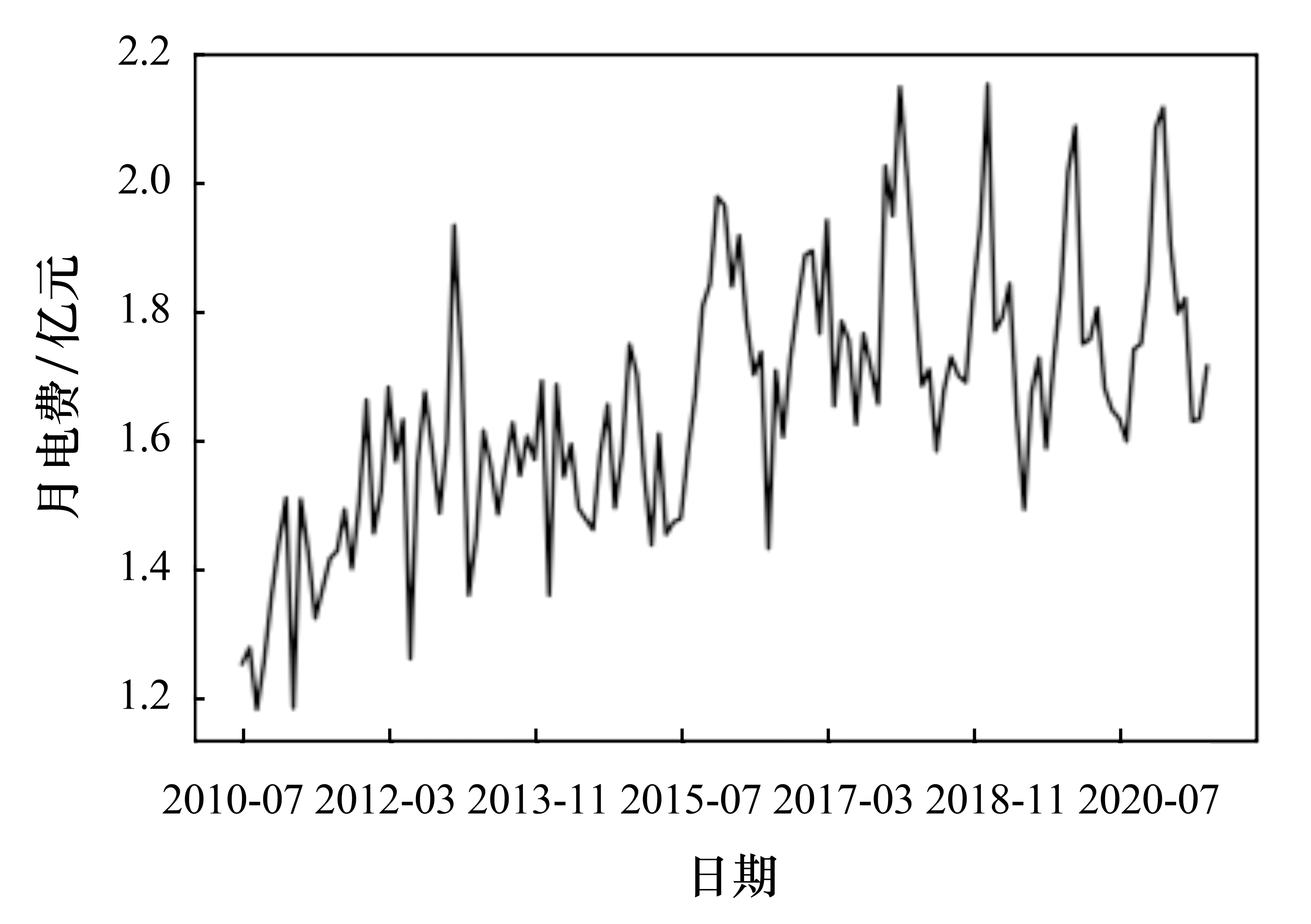
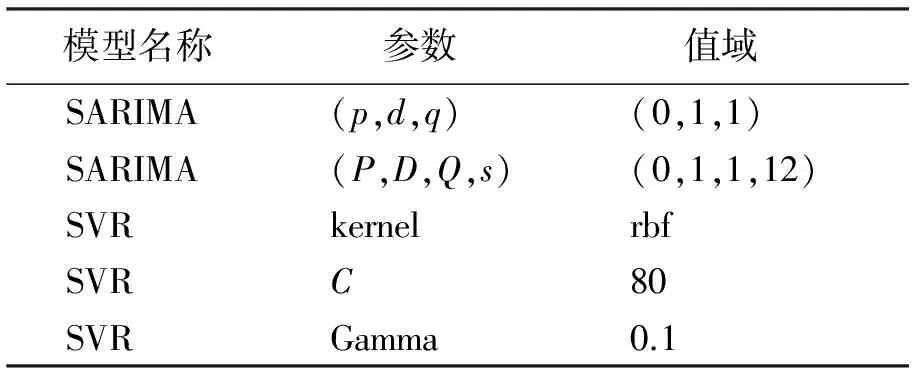
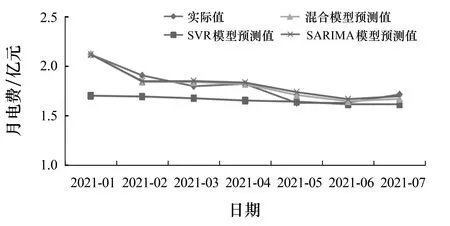
理论上来说,求解b值可通过选取任意一个满足0<αi (9) (10) SARIMA - SVR混合模型的流程如图2所示. 图2 SARIMA - SVR混合模型的建模流程 2.1.1数据集 本文采用的数据资料是国网延边供电公司2010年7月至2021年7月的月电费回收数据,该数据的时序图如图3所示. 图3 月电费收入的时序图 实验时,本文将全部数据按时间段划分为训练集和测试集.其中2010年7月至2020年12月的月电费收入为训练集,2021年1月至2021年7月的月电费收入为测试集.考虑到电费收入数据在不同季节和特殊日期的波动情况,本文采用3种影响特征(见表1)预测SARIMA - SVR混合模型的有效性. 表1 影响电费收入预测的因素 2.1.2数据平稳性检验 由于需要判断原始时间序列数据是否平稳,因此需要对序列的平稳性进行检验.平稳性检验的方法有两种:一种是通过时序图的形状和走势来判断平稳性;另一种是通过构造检验统计量来判断平稳性.由于第2种方法中的单位根检验(ADF)能够准确地判断序列平稳性,因此本文采用单位根检验方法来判断原始序列和差分之后的序列是否平稳. 2.1.3最优参数 赤池信息准则(Akaike information criterion,AIC)和贝叶斯信息准则(Bayesian information criterion, BIC)是衡量统计模型拟合是否优良的常用标准,其表达式为: AIC=2k-2 lnL, (11) BIC=klnn-2 lnL. (12) 其中,k为模型参数个数,n为样本数量,L为似然函数.本文以AIC准则和BIC准则为依据,使用AUTO - ARIMA函数(python 3.8版)选取最优参数,得到的具体参数设置如表2所示. 表2 SARIMA - SVR混合模型的参数设置 2.2.1误差分析 为了对比分析模型的预测结果,在进行精准度评估时,本文选取平均绝对百分比误差(MAPE)作为模型的评价标准.平均绝对百分比误差的计算公式为: (13) 2.2.2平稳性检验 对原始数据进行单位根检验显示,其P值(0.137 728)远大于0.05,说明原始数据是不平稳序列,需要进行差分处理.为此本文利用表2中的参数对原始数据进行差分处理,然后再对差分后的数据进行计算得到了时间序列数据的自相关系数(ACF)和偏自相关系数(PACF),如图4所示.由图4可以看出,差分后的数据已趋于平稳.另外,根据平稳性检验原理对差分后的数据进行单位根检验得其P值远小于0.05,这进一步说明差分后的数据是平稳的. 图4 序列的自相关系数和偏自相关系数 2.2.3残差分析 对预测数据的残差进行白噪声分析后得其P值远小于标准值0.05,由此表明得到的SARIMA模型的残差不是一组白噪声序列.这说明残差中还有有用的信息,需进一步提取有效信息.提取有效信息的方法是:首先对残差序列进行支持向量回归分析,以此得到残差的预测值;然后将残差的预测值和SARIMA的预测值相加,以此得到更为接近实际值的预测值. 2.2.4对比分析 为了验证SARIMA - SVR混合模型的预测准确性,在相同的测试集下将SARIMA - SVR混合模型与SARIMA模型、SVR模型进行了对比实验.两种模型的参数值如表3所示,该参数值可以使SARIMA模型和SVR模型的整体效果达到最佳. 表3 SARIMA、SVR模型的参数设置 为了更加直观地观察预测结果,将各模型的实际值与预测值进行了可视化处理,如图5所示.由图5可以看出, SARIMA - SVR混合模型的预测精准度与实际值最为接近,由此表明混合模型的拟合效果较好. 图5 各模型的预测结果 3种模型的MAPE值如表4所示.由表4可以看出, SARIMA - SVR混合模型的数据预测效果显著优于其他两种模型,其中SARIMA - SVR混合模型的MAPE值比SARIMA模型降低了13.50%,比SVR模型降低了73.75%.其原因是SARIMA - SVR混合模型将电费时间序列中包含的主要趋势融入到了模型中进行了残差分析,由此使得SARIMA模型的预测结果得到进一步修正,从而达到了更好的预测效果. 表4 3种模型的预测效果 利用本文构建的SARIMA - SVR混合模型对电费收入进行预测表明,SARIMA - SVR混合模型的预测精度显著优于单一的SARIMA模型和SVR模型,因此该模型可为今后电费收入预测方面的研究提供参考.由于本文在研究中使用的月电费收入数据相对较少,在寻找训练模型的变量特征方面仍存在不足;因此,在今后的研究中,我们将进一步挖掘数据,如量化居民缴费的心理因素、流动人口、消费者指数等,以此得到更多、更合适的变量特征来训练模型,从而进一步提高模型的准确度.1.3 SARIMA - SVR混合模型
2 实证分析
2.1 数据处理


2.2 结果分析
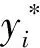


3 结论
