区间数刻画属性值下的两种多属性决策新算法

朱国成, 陈利群

( 广东创新科技职业学院 通识教育学院， 广东 东莞 523960 )

0 引言

目前，研究属性信息数据为区间数的多属性决策问题的方法主要有决策专家的权重计算方法[1]、属性权重的计算方法[2]、决策算法[3]、区间数的决策矩阵规范化处理方法[4]等.2018年，李宝萍等[5]在Maclaurin对称平均算子的基础上定义了概率犹豫模糊Maclaurin对称平均算子和概率犹豫模糊Maclaurin对称加权平均算子，并将Maclaurin对称平均算子用于求解概率犹豫模糊环境决策问题，结果显示该方法具有较好的决策效果.在文献[5]的方法基础上，本文将Maclaurin对称平均算子用于求解属性信息数据为区间数的多属性决策问题中(算法1)，该算法以各方案在相同属性上的差异程度对各方案进行排序.2002年，徐泽水等[6]定义了一个区间数可能度公式，并利用该公式建立了一个可以对各方案进行两两比较的可能度互补判断矩阵，且通过求解该矩阵实现了对方案的排序.在文献[6]的方法基础上，本文利用区间数的积型贴近度公式建立了一个在所有属性上可以进行积型模糊互补判断的矩阵，并通过求解该矩阵对应的排序向量大小来区分各方案的优劣(算法2).对算法1和算法2进行案例分析表明,不同的决策思路不会影响方案的排序结果.

1 基础知识

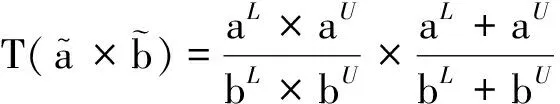
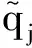
定义6令ai(i=1,2,…,n)为一组非负实数，且r=1,2,…,n.若

(1)

1)对于任意的i, 若ai=a≥0, 则MSM(r)(a1,a2,…,an)=a;

2)对于任意的i, 若0≤ai≤bi, 则有MSM(r)(a1,a2,…,an)≤MSM(r)(b1,b2,…,bn);

3)对于任意的ai≥0, 有min(a1,a2,…,an)≤MSM(r)(a1,a2,…,an)≤max(a1,a2,…,an).

2 两种决策算法的决策步骤

2.1 算法1的决策步骤

根据定义3得算法1的决策步骤为:

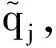
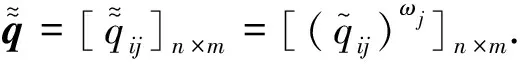
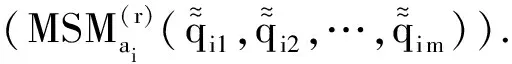
第6步 决策分析与比较.

第7步 结束.

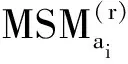
2.2 算法2的决策步骤

根据定义3得算法2的决策步骤为:

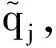
第7步 根据排序向量η的分量ηi大小对方案进行排序, 最大的ηi值所对应的方案ai为优.

第8步 比较排序结果.

第9步 结束.

3 数值算例

由某高职院校领导组成的考核小组分别从教学建设项目(G1)、党建学务项目(G2)、行政管理项目(G3)、社会服务项目(G4)等4个方面对管理学院(a1)、财经学院(a2)、智能制造学院(a3)、建筑与艺术设计学院(a4)、信息工程学院(a5)等5个二级学院进行年终考核.考核所得分数经过技术处理后以区间数形式给出,见表1.根据表1，利用算法1和算法2分别求出各自算法的考核排名结果.已知4个考核因素的权重分别为ω=(0.35,0.3,0.15,0.2)T.

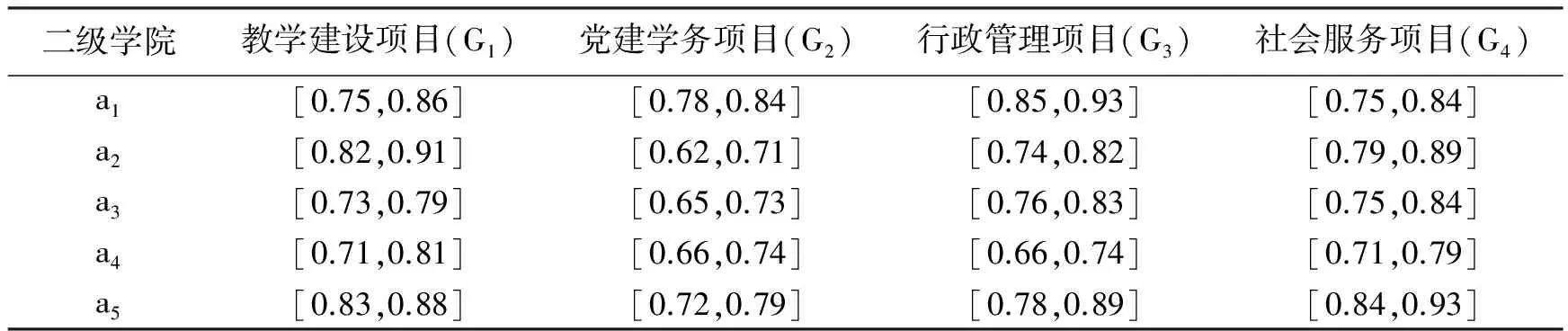
表1 考核评分表

3.1 算法1的计算过程及结果

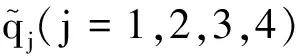
3.2 算法2的计算过程及结果

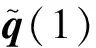
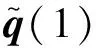
同理可得：

再次，汇总各方案的总排序向量η， 由此得到各方案的总排序向量为η=(η1,η2,η3,η4,η5)T=(4.879 1,4.181 3,3.474 3,3.128 4,4.976 6)T.由该结果可得方案的排序结果为a5≻a1≻a2≻a3≻a4，该结果与算法1的排序结果相同.

3.3 两种决策算法与其他决策算法的比较

由上述可知，算法1和算法2的决策思路虽然不同,但对方案的排序结果相同.为了进一步确定算法1和算法2决策结果的有效性,本文利用文献[8]中的算法(对不同方案的属性进行两两测度后，通过比较不同方案的属性优劣个数进行方案排序)对案例中的各二级学院的考核分数进行了排序，结果显示其排序结果与算法1和算法2的排序结果相同.该结果进一步表明，决策过程或者决策模型不会影响方案的排序.

4 结语

本文研究表明，用不同视角建立的两种决策算法都能解决决策信息数据为区间数的多属性决策问题,而且排序结果不受决策过程或者决策模型的影响.其中:算法1拓宽了Maclaurin对称平均算子的应用范围；算法2(利用积型模糊互补判断矩阵进行决策)有别于传统的模糊互补判断矩阵、模糊一致性矩阵等决策方法，丰富了利用模糊判断矩阵解决区间信息多属性决策问题的方法.在今后的研究中，我们将进一步研究不同决策视角下的不同决策信息数据的多属性决策方法.