冲击荷载下C型G550冷弯钢的断裂机理研究
2022-01-14张子凌岑志波李佰树汪家炜
张子凌, 岑志波, 蒋 磊, 李佰树, 汪家炜, 张 浩, 朱 珏*
冲击荷载下C型G550冷弯钢的断裂机理研究
张子凌1, 岑志波2, 蒋 磊2, 李佰树1, 汪家炜1, 张 浩1, 朱 珏1*
(1.宁波大学 冲击与安全工程教育部重点实验室, 浙江 宁波 315211; 2.宁波市特种设备检验研究院, 浙江 宁波 315048)
以C型G550薄壁冷弯钢构件为研究对象, 通过材料在不同应变率下的拉伸实验和数值模拟数据得到Johnson-Cook(J-C)本构模型和Johnson-Cook失效模型参数. 通过Abaqus软件模拟了不同冲击荷载作用下C型冷弯钢构件撕裂破坏的全过程, 利用落锤装置轴向冲击试验进行对比, 其实验结果与有限元数值模拟结果有良好的一致性. 此外, 对冲击试样撕裂断口进行微观形貌分析, 得到构件的断裂机理. 结果表明: 随着冲击速度的提高, 冲击力对构件的加载时间增加, 构件需要较大的塑性变形来吸收冲击能量; 冲击速度越高, 裂纹扩展功所占吸收冲击能量的比例越大, 显示出高速下裂纹扩展的能力越好; 冲击速度较高时, 以脆性断裂为主, 断口出现解理面, 甚至在高速变形时发生了绝热剪切破坏.
冷弯钢; Johnson-Cook模型; 有限元模拟; 撕裂; 塑性变形
冷弯钢构件因高强、轻质和易加工等优越性能, 近年来在建筑结构、桥梁交通和军事设施等领域得到了越来越广泛的应用. 由于冷弯钢结构在实际工程中经常承受冲击荷载[1-2], 如果构件的动态破坏机制没有得到有效掌握, 在实际建设和应用过程中可能会造成严重后果和重大经济损失. 因此, 研究冷弯型钢结构在动态冲击荷载作用下的安全性评价具有重要现实意义.
目前, 国内外一些专家学者对薄壁结构在动态冲击作用下的破坏进行了不同程度的研究. 1987年, Kleiber等[3]基于系统刚度剪切矩阵为零的条件, 提出Kleiber-Kotula-Saran(K-K-S)准则, 并且找到了极限脉冲荷载幅值. 2007年, Kubiak[4]研究在一定时长脉冲下, 薄壁构件整体与局部交互动态失稳的边界脉冲幅值. Wang等[5]对受轴向冲击荷载的铝合金板条进行研究, 发现高阶模态的屈曲影响着低阶模态的半波长. 之后魏勇等[6]通过对受冲击构件残余变形进行分析, 定性发现了屈曲模态的变化与叠加. 杨长青[7]对结构钢材料高速冲击下的断裂行为进行了研究, 表明断裂过程是沿绝热剪切带开裂的损伤演化过程. 廖芳芳等[8]对高强钢断裂性能的试验研究发现, 应力状态对高强钢的延性与微观断裂机制有着显著的影响. 李发超等[9]通过对比薄壁冷弯钢完好试件与受损试件的极限承载能力, 分析得到了试样剩余承载力系数与冲量的线性关系. 李佰树等[10]发现薄壁冷弯钢构件受到外部冲击作用后, 会产生动态屈曲, 并随着冲击荷载增大, 发展为明显的塑性变形.
根据以上分析可知, 薄壁构件的冲击断裂行为研究成果较少, 很有必要对其进行进一步研究. 本文通过不同荷载下G550冷弯钢构件有限元仿真分析和轴向落锤冲击试验进行对比, 并结合观察试样断口微观形貌来对冷弯钢构件断裂的机理进行探索.
1 拉伸试验和J-C本构模型
1.1 材料率相关拉伸试验
本拉伸试验材料采用高强度冷弯结构钢G550, 试验试样为沿着同一卷钢材轧制方向线切割切取, 试验环境为室温环境. 在小型INSTRON 5966双立柱式材料拉伸试验机上进行10-4~100s-1应变率的准静态和低应变率拉伸试验. 在HTM 5020材料高速拉伸机上进行100~102s-1应变率的中高应变率试验. 准静态与动态拉伸试样均按照国标GB/T 228-2010《金属材料室温拉伸实验方法》的规定设计[11]. 试样厚度为1.15mm, 形状尺寸如图1所示.
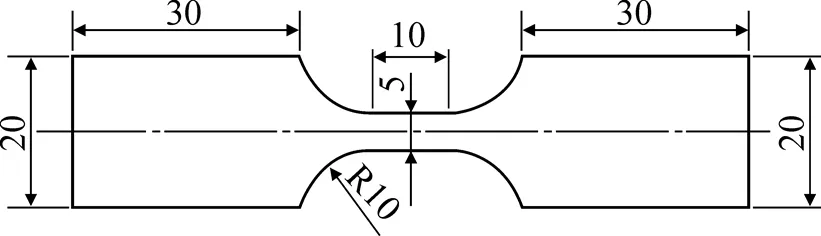
图1 G550冷弯钢材料拉伸试样设计尺寸(mm)
图2为准静态、低应变率及中高应变率下G550冷弯钢材料在拉伸试验中得到的工程应力—应变曲线. 从图中可以看出, 在某个应变率状态下, 此阶段曲线接近为一段平台区, 说明该冷弯钢试件经过屈服点后的极限应力没有明显增强趋势[12]. 此外还可发现, 在低应变率时的应力—应变曲线相对较为接近, 而在较高应变率下的应力—应变曲线幅度随着应变率的增加有显著的提高, 存在着较明显的应变率强化效应.
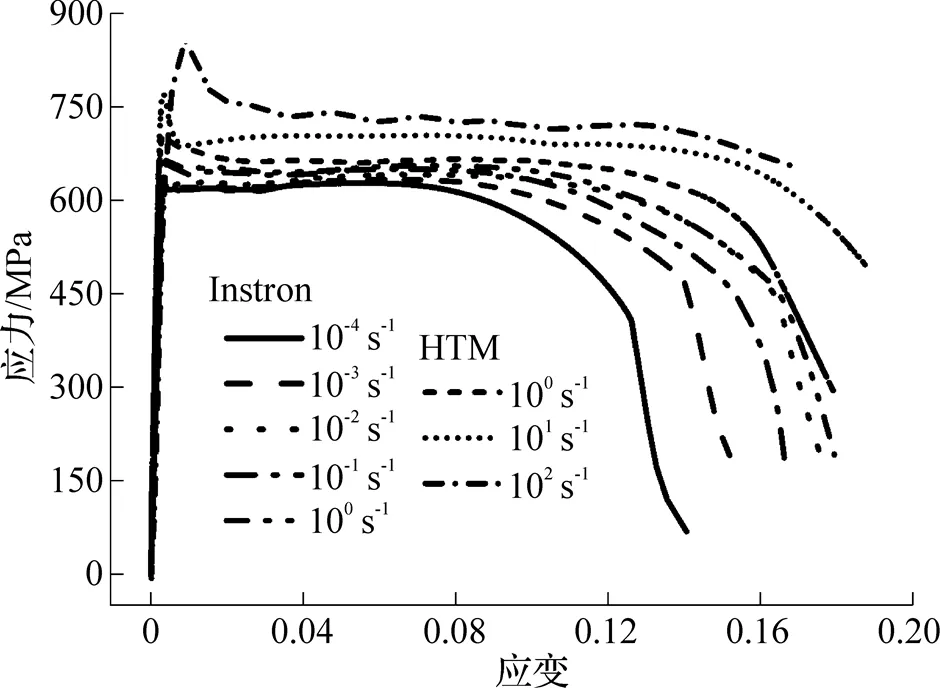
图2 系列应变率的G550冷弯钢应力—应变曲线
1.2 J-C本构模型
Johnson-Cook模型是与材料应变率相关的动态本构关系. 选取Johnson-Cook模型拟合G550冷弯钢的本构关系, 其表达式为:
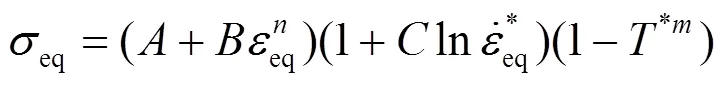
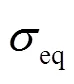
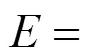
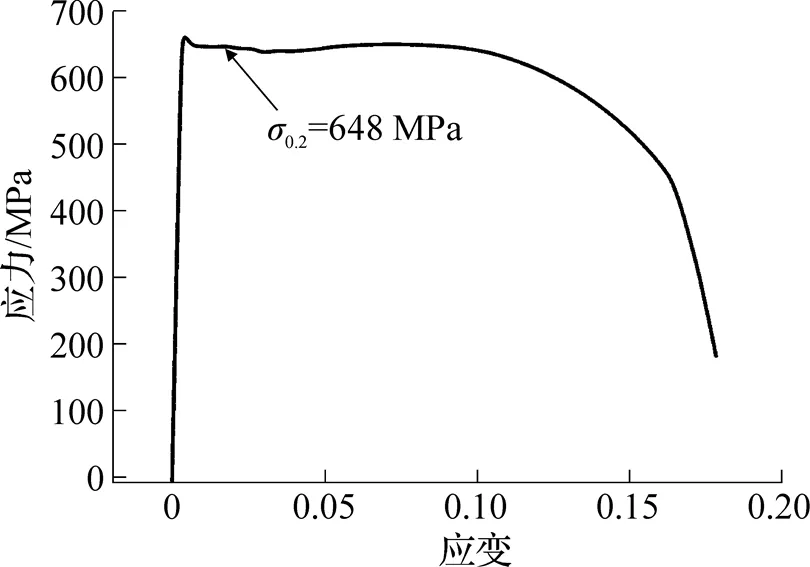
图3 参考应变率1 s-1的应力—应变曲线
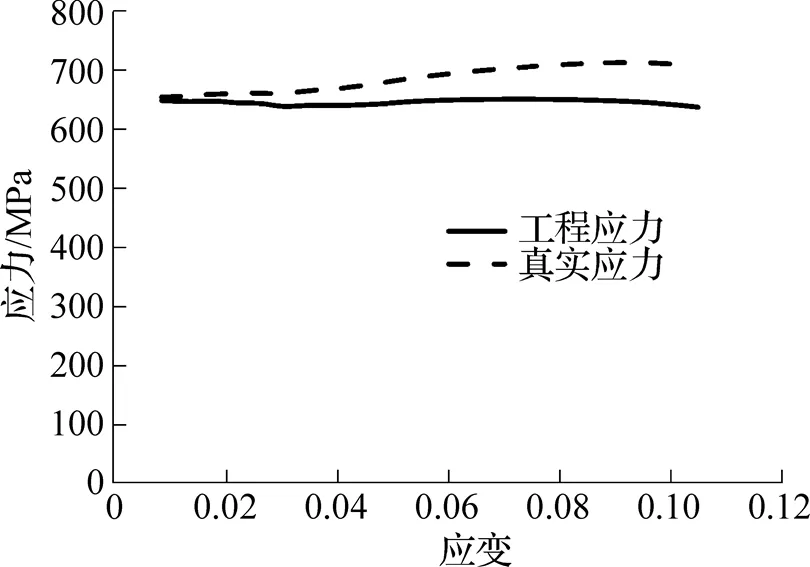
图4 塑性阶段的工程和真实应力—应变的关系
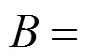
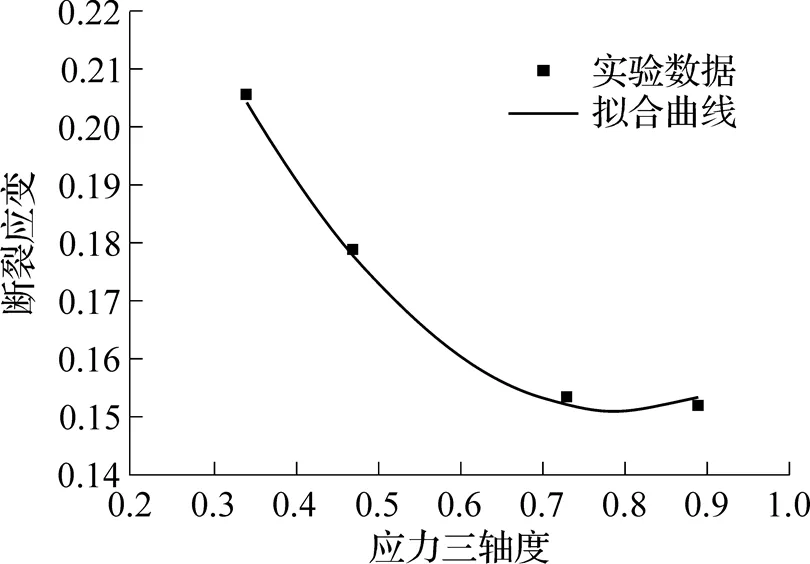
图5 塑性状态到极限应力前部分的曲线拟合
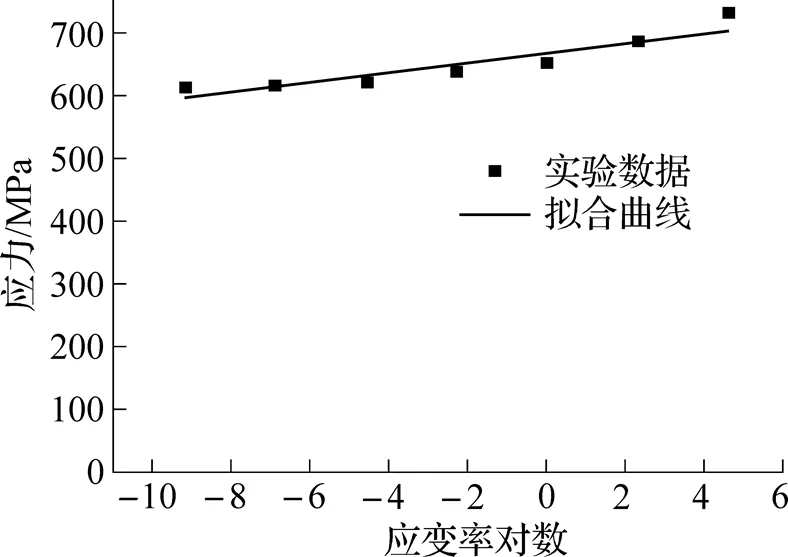
图6 不同应变率下对应的屈服应力
2 缺口试样拉伸试验及J-C断裂失效准则
2.1 缺口试样拉伸试验
缺口拉伸试样使用G550薄壁冷弯钢材料, 试样中间两端缺口采用直径为4、6和8mm的半圆形切口(图7). 在小型INSTRON材料拉伸试验机上进行室温条件下应变率为1s-1的拉伸试样试验, 选取发生在断裂处5mm的试样作为标距段. 该拉伸试验是为了从试验中得到各个试样发生断裂时的应变值, 进而基于已经获得的本构参数, 通过缺口试样拉伸数值模拟来获取材料应力三轴度关于断裂应变的关系.
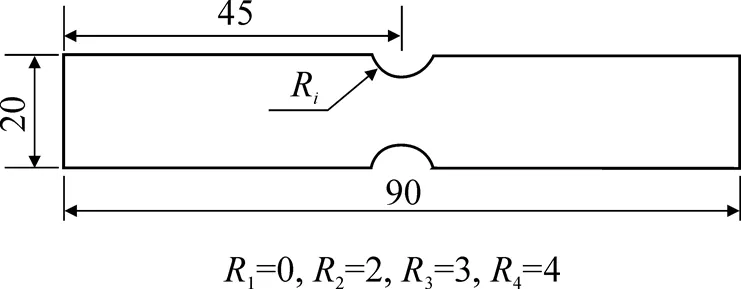
图7 平板拉伸试样不同缺口半径的拉伸试样(mm)
构件材料拉伸过程中, 其在最小横截面位置发生断裂, 而此位置即为试件上出现最大应力的地方. 所以通过采集此最小截面上的应力三轴度, 作为试样计算断裂的应力三轴度值. 通过Abaqus等仿真软件来模拟试样动态变形的整个过程, 从而得到构件在任意时间点的应力三轴度数值[15-16]. 图8即为有限元仿真中, 各个缺口试样拉伸过程中的应力三轴度分布情况.
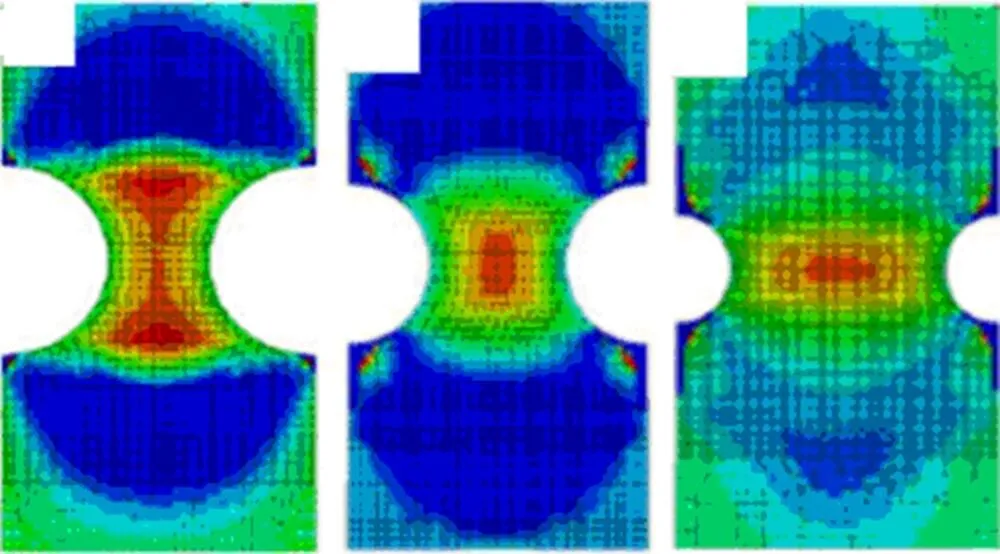
图8 各个缺口试样应力三轴度分布
平板拉伸试样最小截面路径上的应力三轴度很稳定, 通常其值约为0.34. 两侧缺口半圆弧开始的位置三轴度最小, 而在靠近中间最窄的位置应力三轴度值最大. 同时, 随着半圆弧型缺口半径的增大, 应力三轴度值会随之减小. 经有限元仿真可以得到, 缺口直径为8mm时, 最大应力三轴度的值为0.47; 缺口直径为6mm时, 最大三轴度的值为0.73, 缺口直径为4mm时, 最大三轴度的值为0.89.
2.2 J-C断裂失效准则
Johnson-Cook断裂失效准则作为涉及断裂问题的有效参数模型, 在结构动态冲击与材料的非线性大变形中有着较为广泛的应用. 同时和上节中拟合得到的本构关系模型相统一, 在这里选取Johnson-Cook断裂准则作为G550冷弯钢缺口拉伸试验的拟合模型.
Johnson-Cook断裂准则一般表达式如下:
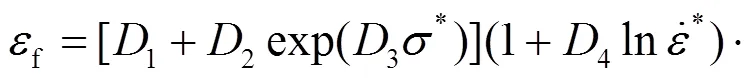
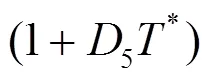
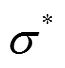
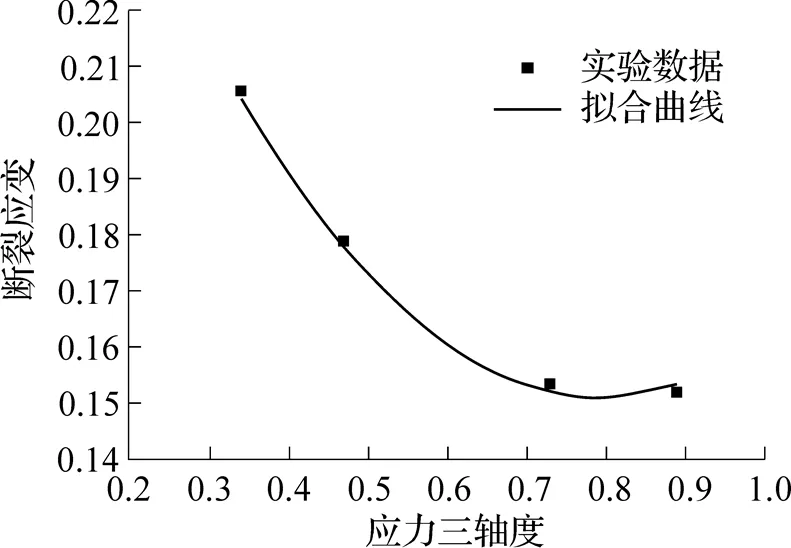
图9 不同缺口试件的断裂应变与应力三轴度的关系
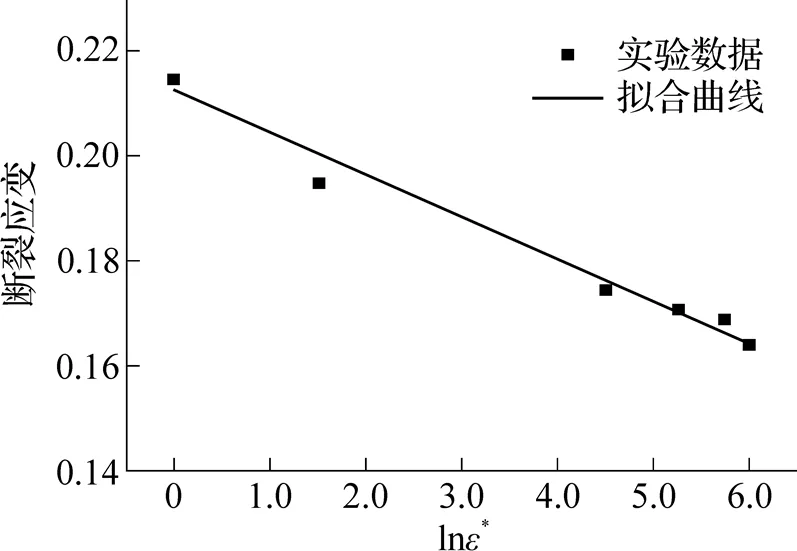
图10 拉伸应变率的自然对数值与相应断裂应变的关系
3 有限元仿真和轴向冲击试验对比结果分析
3.1 有限元建模
在Abaqus有限元软件中, C型薄壁冷弯钢构件采用壳体单元构建, 其腹板高度和翼缘宽度分别为60mm和30mm, 卷边长10mm, 试件长度为200mm, 厚度为1.15mm. 落锤装置的上部冲击端和下方底座平台均简化成不可变形的刚性平板, 采用离散型刚体单元构建, 尺寸为200mm×200 mm的方形平板, 冷弯钢构件腹板下部由一对长50mm、高55mm的磁力座固定在底座上面, 防止构件被击飞. 建立三维模型如图11(a)所示, 将C型冷弯钢构件采用壳体Quad为主的Advancing front算法的自由划分方式, 网格单元为S4R的缩减积分单元. 同时, 上下刚性平板采用离散型刚体单元R3D4. 为了减少不必要的计算, 刚性单元的网格尺寸设置得要大于薄壁冷弯钢构件的网格尺寸. 模型网格划分情况如图11(b)所示. 由于G550冷弯钢材料在动态冲击下会有较为明显的应变率相关强化效应, 因此使用得到的Johnson-Cook本构模型参数作为该试验钢的本构材料属性关系. 同时设置材料的弹性模量为198GPa, 泊松比为0.3. 为了对高速轴向冲击下薄壁冷弯钢构件的撕裂破坏情况进行仿真模拟和研究, 使用得到的Johnson- Cook断裂准则参数作为该试验钢构件撕裂的判断依据.
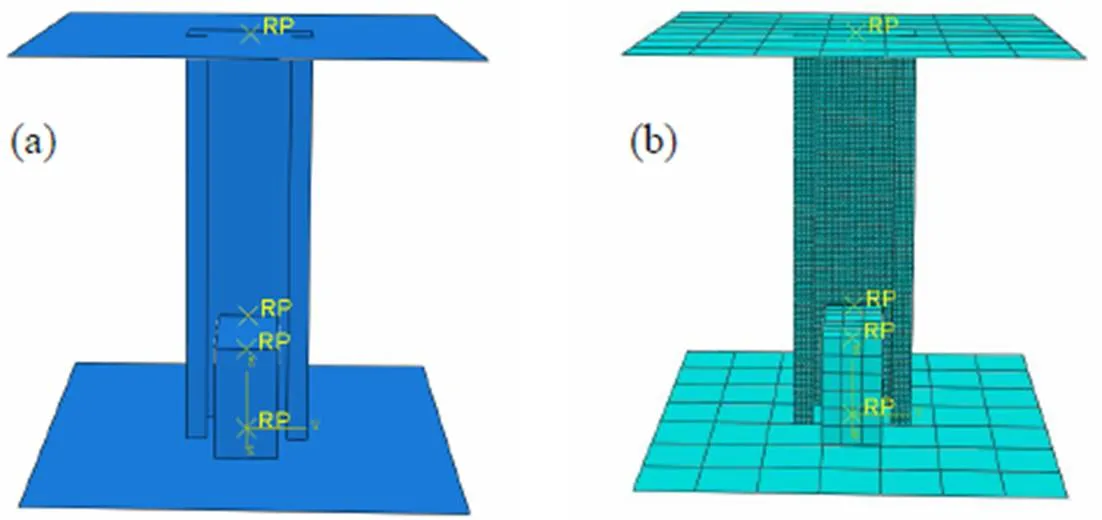
图11 冷弯钢构件落锤冲击三维模型(a)及网格划分(b)
针对冲击与爆炸这种高速、大变形的动态力学有限元仿真问题[17], 构件在受到轴向冲击荷载作用下, 结构内部会发生复杂的动态接触关系. 在本文模型的接触关系上, 我们首先使用通用接触来定义各部件间的接触关系, 然后针对C型钢构件加入可以反映其内部结构接触作用关系的“显性自我接触”. 针对构件顶端和锤头平板, 我们使用面-面接触(Surface-to-Surface Contact), 这样可以方便地提取锤头冲击时, 作用于构件顶端的冲击荷载等结果. 在接触属性上, 设定为罚函数算法, 部件间的法向为硬接触.
由于冷弯钢构件在进行轴向冲击试验前(即未受到外部荷载作用时)就已经实际存在着材料缺陷, 因此可以通过薄壁结构轴压的有限元分析引入初始缺陷来诱发构件发生屈曲. 这里取前十阶主要的动态屈曲模态分析[18], 得到构件前十阶的屈曲模态和特征值, 计算特征值倒数和, 然后再计算出每个特征值倒数与倒数和的比值, 作为缺陷因子. 表1即为前十阶屈曲模态特征值与缺陷因子.
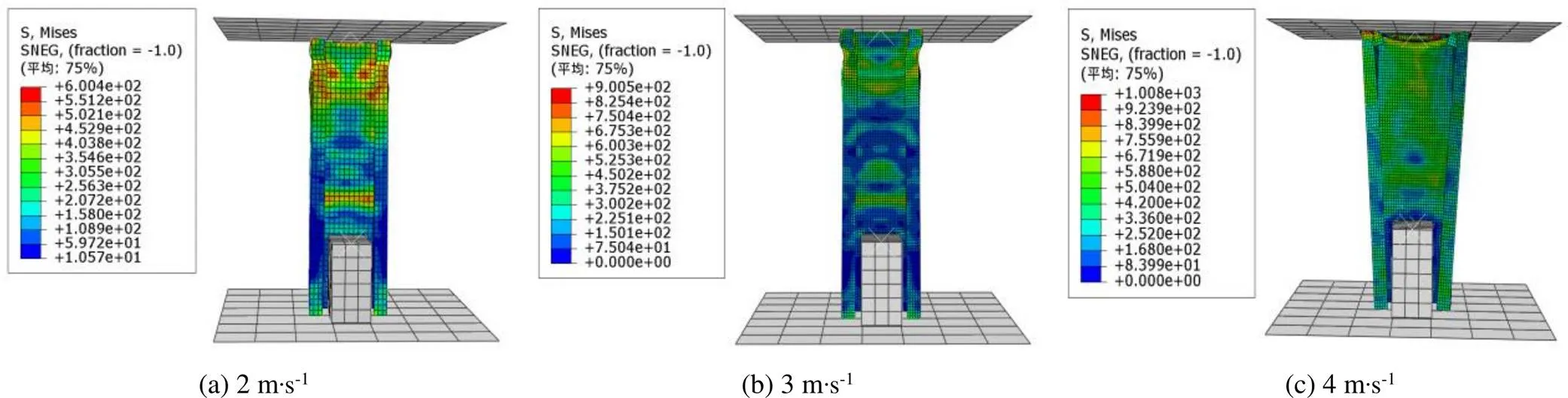
图12 落锤冲击仿真模型冷弯钢构件的残余变形
3.2 有限元仿真结果
对G550薄壁冷弯钢构件在2、3和4m∙s-1时的3种轴向冲击速度进行仿真计算, 得到了不同动态荷载下构件的残余变形情况. 图12是G550冷弯钢构件落锤冲击仿真模型在3种冲击速度下的残余变形. 试件端部在2、3m∙s-1的速度下, 逐步发生了由局部屈曲微变形到卷曲变形的过程. 随着冲击速度的提高, 在4m∙s-1冲击速度下的试件端部发生如折叠等更为复杂的屈曲变形模式, 甚至在折弯位置发生了撕裂破坏现象.
在有限元模型中, 通过将锤头冲击端简化成刚性平面对构件顶端进行轴向冲击加载, 提取冲击过程中两者的接触力, 分析锤头对构件的冲击荷载, 图13为不同速度下构件承受的冲击力—时间曲线. 从图中可以明显看出, 当冲击力第1次达到峰值后, 并没有下降为0, 而是又上升一小段, 出现第2个峰值, 且第2次达到的峰值均明显大于第1次的峰值. 此外在冲击时, 应力波的存在会导致冲击力幅度的部分变化[19].

图13 不同速度下的冲击力—时间曲线
为研究冷弯钢构件在锤头冲击端的轴向荷载作用下出现二次峰值的成因, 对构件受冲击端主要质点位置的行为变化进行分析(图14). 提取构件受冲击端腹板翼缘和卷边中心质点的速度—时间曲线和位移—时间曲线, 同时也对相同时间坐标的冲击力变化进行分析.
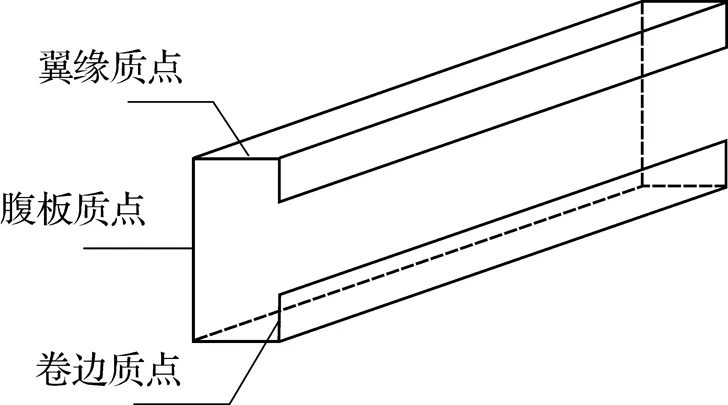
图14 构件受冲击端腹板、翼缘和卷边中心质点位置
图15为3m∙s-1落锤冲击下, G550冷弯钢构件质点的位移—时间和速度—时间曲线. 由图可见, 最先脱离锤头的是构件的卷边位置, 且其速度明显大于锤头冲击速度, 与其他2个质点部位的位移相比, 卷边位置的位移也是最大. 说明卷边率先达到屈服, 冲击力达到第1次峰值. 卷边的位移随着应力波的传播持续增大, 并且伴随有撕裂痕迹. 构件的腹板在后期与锤头也发生了微小分离, 从而造成了冲击力出现第2次峰值, 而翼缘在冲击过程中始终与锤头接触.
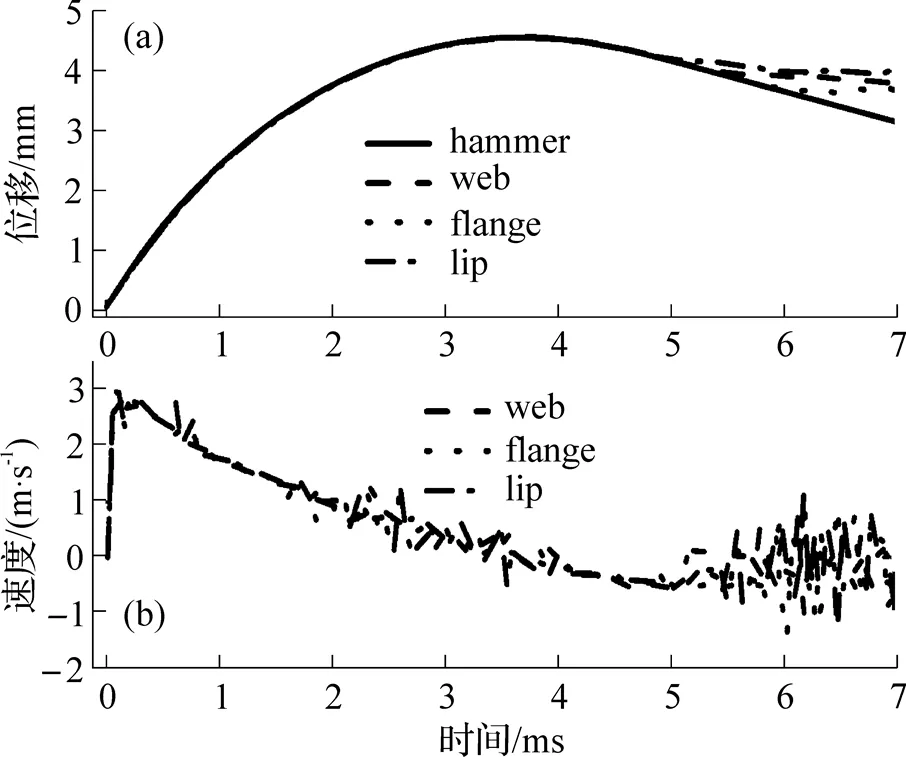
图15 钢构件质点的位移—时间(a)和速度—时间(b)曲线
根据示波冲击试验原理, 可按照一个平面坐标图的面积来计算出裂纹形成功和扩展功的数值, 其纵坐标是荷载的变化, 横坐标是时间变化. 它以荷载的峰值点为分界, 荷载上升阶段所占的面积可理解为裂纹形成功, 荷载下降阶段所占的面积可理解为裂纹扩展功[20]. 表2是从冲击力时程曲线计算结果中得到的不同速度下构件端部的冲击试验结果. 从表中数据可见, 构件承受的最大冲击力随着冲击速度的提高而随之增大. 冲击速度继续提高, 构件将通过较大的塑性变形来吸收冲击能量. 直至构件无法通过塑性变形承受动态荷载, 将伴随撕裂破坏现象的发生. 冲击速度2m∙s-1时, 裂纹扩展功所占冲击能量比例最小, 显示出2m∙s-1低速下裂纹扩展的能力最低; 冲击速度4m∙s-1时, 裂纹扩展功所占冲击能量比例最大, 显示出4m∙s-1高速下裂纹扩展的能力最好.
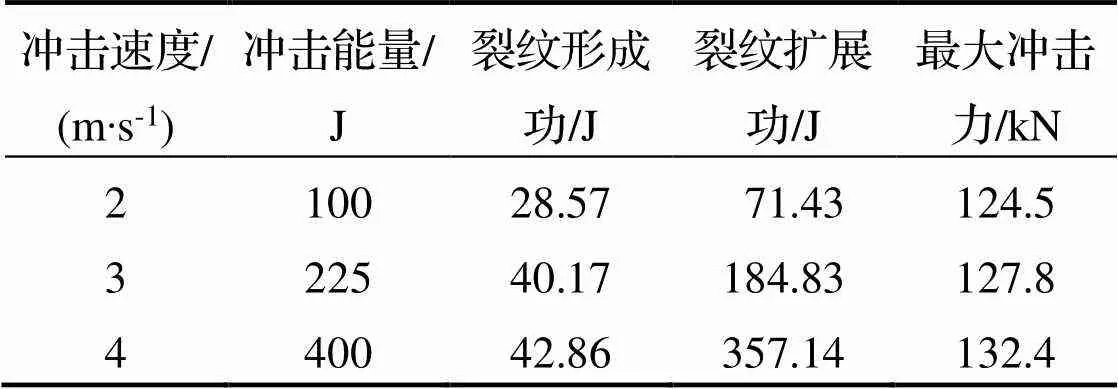
表2 不同速度下构件端部的冲击试验结果
3.3 C型钢构件轴向冲击试验
利用大型落锤装置对C型冷弯薄壁钢构件进行2~4m∙s-1速度下的轴向冲击试验. 图16为不同冲击速度下试件的残余变形(自左至右依次是2、3和4m∙s-1的轴向冲击速度). 通过观察试验结果发现, 试件在2、3m∙s-1的速度下逐步发生了由局部屈曲和畸变屈曲[21]结合(主要以局部屈曲为主)的微变形到卷曲变形的过程. 随着冲击速度的提高, 在4m∙s-1冲击速度下的试件端部发生如折叠等更为复杂的屈曲变形模式, 在折弯位置发生了撕裂破坏现象. 这与冷弯钢有限元仿真得到的结果比较一致.

图16 落锤冲击试件的残余变形
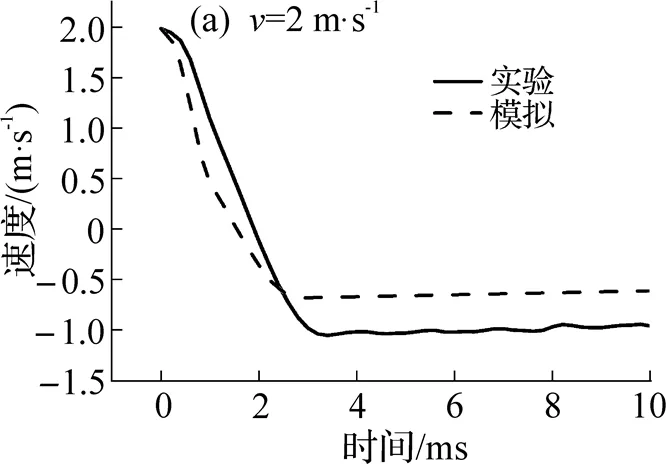
通过使用高速相机和散斑分析方法, 可以得到构件轴向冲击下, 整个屈曲变形过程中锤头下落的速度变化曲线. 由图17可见, 试验值对锤头速度变化的采集结果与有限元仿真模拟的结果比较接近, 从而说明落锤轴向冲击有限元分析模型的可靠性.
4 冲击试样断口微观分析
在冲击荷载作用下, 断口的特征、性状和断裂机制会随着冲击速度的变化而变化. 一般情况下,冲击断口存在3个区域, 即纤维区、放射区以及剪切唇区(图18). 裂纹的扩展大多造成断裂的发生, 而裂纹扩展所需的能量大部分消耗于塑性变形, 塑性变形区尺寸越大, 塑性变形功消耗越大, 冲击断裂韧性也相应越大[22].
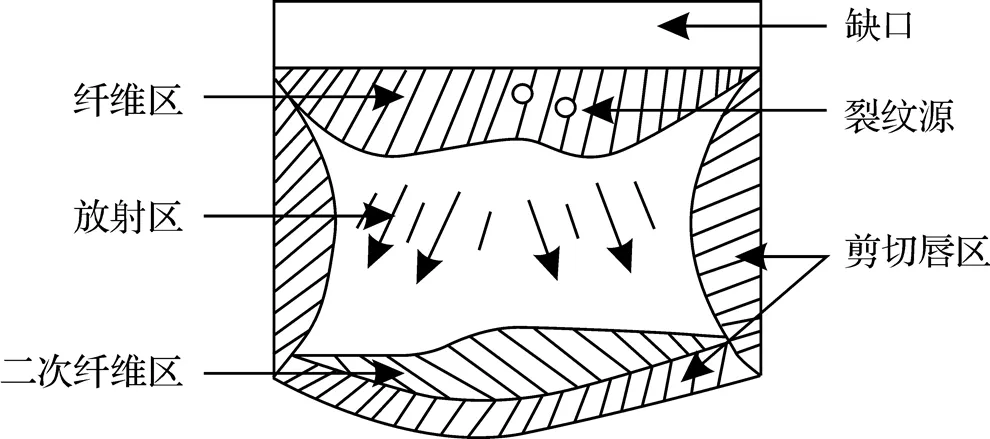
图18 冲击断口形貌示意图

图19 G550冷弯钢冲击断口裂纹萌生区微观形貌
通过线切割截取撕裂断口处小部分不同冲击速度下的试样, 将其放在SU5000电镜下观察, 来分析断口的微观形貌. 图19是冷弯钢试样在不同冲击速度下裂纹萌生区的微观形貌. 从图中可以看出, 随着冲击速度的提高, 冷弯钢试样裂纹萌生区的断裂机制也发生了显著的变化. 冲击速度为2m∙s-1时, 在裂纹萌生区呈现韧窝状断裂的断口形貌; 冲击速度为3m∙s-1时, 在裂纹萌生区呈现“解理状+少量韧窝状断裂”的断口形貌; 而冲击速度为4m∙s-1时, 在裂纹萌生区呈现“解理状+韧窝状断裂”的断口形貌. 这说明在冲击荷载作用下, 随着冲击速度的增大, 裂纹萌生区的断裂机制由韧性断裂向脆性断裂转变, 此外发现在4m∙s-1下塑性变形的区域中, 存在一些白色的亮带, 即绝热剪切带(ASB), 说明裂纹裂尖产生高速变形, 导致绝热剪切现象[23].
5 结论
本文通过有限元仿真, 并结合落锤轴向冲击试验、扫描电镜微观试验对不同荷载下G550冷弯钢构件的动态损伤和断裂行为进行研究, 得出结论如下:
(1)随着冲击速度的提高, 冲击力对构件的加载时间也在增加, 且构件将通过较大的塑性变形来吸收冲击能量. 承受动态荷载达到极限时, 会导致撕裂破坏现象的发生.
(2)冲击速度较低时, 裂纹扩展功所占冲击能量的比例较小, 显示出低速下裂纹扩展的能力较低; 冲击速度较高时, 裂纹扩展功所占冲击能量的比例较大, 显示出高速下有着良好的裂纹扩展能力.
(3)随着冲击速度升高, 断口出现解理面, 裂纹萌生区的断裂机制由韧性断裂向脆性断裂转变, 甚至在高速变形时发生了绝热剪切破坏.
[1] 张旭, 孙国军, 黄栩浩, 等. 轴向冲击下C型冷弯卷边槽钢构件的动力响应[J]. 爆炸与冲击, 2018, 38(4):841- 846.
[2] 陈高哲, 霍静思, 崔鹏飞. 预加轴力下加强冷弯T型方钢管节点抗冲击试验研究[J]. 船舶力学, 2017(S1):543- 553.
[3] Kleiber M, Kotula W, Saran M. Numerical analysis of dynamic quasi-bifurcation[J]. Engineering Computations, 1987, 4(1):48-52.
[4] Kubiak T. Criteria of dynamic buckling estimation of thin-walled structures[J]. Thin-Walled Structures, 2007, 45(10/11):888-892.
[5] Wang A W, Tian W Y. Mechanism of buckling development in elastic bars subjected to axial impact[J]. International Journal of Impact Engineering, 2007, 34(2): 232-252.
[6] 魏勇, 朱兆祥, 李永池. 轴向冲击载荷作用下直杆弹性动态屈曲的研究[J]. 实验力学, 1988, 3(3):55-61.
[7] 杨常青. 结构钢动态断裂机理[J]. 太原师范学院学报(自然科学版), 2007, 6(3):135-137.
[8] 廖芳芳, 李文超, 周天华. Q460D高强钢断裂性能试验研究及断裂准则的校准[J]. 西安建筑科技大学学报(自然科学版), 2016, 48(3):362-370.
[9] 李发超, 张旭, 赵伟欣, 等. 某C型冷弯薄壁钢构件冲击后的极限承载力研究[J]. 工业建筑, 2019, 49(5):133- 138.
[10] 李佰树, 李发超, 吴梦景, 等. Z型Q345冷弯钢构件率相关本构模型下的动态冲击失稳研究[J]. 宁波大学学报(理工版), 2020, 33(6):45-52.
[11] GB/T228-2002. 金属材料室温拉伸试验方法[S].
[12] 周天华, 周绪红, 何保康, 等. G550级高强薄板钢材的材性及应用[J]. 建筑科学与工程学报, 2005, 22(2):43- 46.
[13] 黄西成, 胡文军. Johnson-Cook本构参数的确定方法[C]//第六届全国爆炸力学实验技术学术会议论文集. 长沙, 2010:313-320.
[14] 林莉, 支旭东, 范锋, 等. Q235B钢Johnson-Cook模型参数的确定[J]. 振动与冲击, 2014, 33(9):153-158; 172.
[15] 谢凡, 张涛, 陈继恩, 等. 应力三轴度的有限元计算修正[J]. 爆炸与冲击, 2012, 32(1):8-14.
[16] 贾东, 黄西成, 莫军. 基于应变路径和分布效应的应力三轴度确定方法[J]. 科学技术与工程, 2013, 13(10): 2625-2629; 2634.
[17] 肖刚. 结构在约束下和动力作用下屈曲的数值模拟[D]. 上海: 上海交通大学, 2008.
[18] Wang A W, Tian W Y. Characteristic-value analysis for plastic dynamic buckling of columns under elastoplastic compression waves[J]. International Journal of Non- Linear Mechanics, 2003, 38(5):615-628.
[19] 王礼立. 应力波基础[M]. 2版. 北京: 国防工业出版社, 2005.
[20] 尹士科, 喻萍, 王移山. 焊接接头的抗动载断裂特性[J]. 机械制造文摘(焊接分册), 2014(6):1-6.
[21] Lau S C W, Hancock G J. Distortional buckling formulas for channel columns[J]. Journal of Structural Engineering, 1987, 113(5):1063-1078.
[22] 上海交通大学《金属断口分析》编写组. 金属断口分析[M]. 北京: 国防工业出版社, 1979.
[23] 寇绍全. 绝热剪切—–一个值得重视的材料破坏问题[J]. 力学进展, 1979, 9(3):52-59.
Fracture mechanism of G550 channel cold-formed steel under impact load
ZHANG Ziling1, CEN Zhibo2, JIANG Lei2, LI Baishu1, WANG Jiawei1, ZHANG Hao1, ZHU Jue1*
( 1.Key Laboratory of Impact and Safety Engineering of Ministry of Education, Ningbo University, Ningbo 315211, China; 2.Ningbo Special Equipment Inspection and Research Institute, Ningbo 315048, China )
Using G550 channel cold-formed steel members, the Johnson-Cook constitutive model parameters and the Johnson-Cook failure model parameters are determined through the material tensile experiments and numerical simulations under different strain rates. The whole process of tearing failure of channel cold-formed steel members under different impact loads is simulated by ABAQUS software. The axial impact test of the drop hammer device is used for comparison, and the experimental results are in good agreement with the finite element numerical simulation results. In addition, the fracture mechanism of a piece of sample at the tear fracture region is analyzed by microscopic morphology. The results show that with the increase of the impact speed, the loading time of the impact force on the component increases, and the component requires greater plastic deformation to absorb the impact energy. The higher the impact speed, the greater the proportion of the crack growth work to the impact energy, which shows that the ability to prevent crack propagation at high speed is better. When the impact speed is high, brittle fracture is the main cause, during which cleavage surface appears in the fracture surface, and even adiabatic shear failure occurs during deformation.
cold-formed steel; Johnson-Cook model; finite element simulation; tear; plastic deformation
O347
A
1001-5132(2022)01-0090-08
2021−03−25.
宁波大学学报(理工版)网址: http://journallg.nbu.edu.cn/
国家自然科学基金(11972203, 11572162); 浙江省自然科学基金(LY13A020007); 宁波市自然科学基金(202003N4152); 宁波轨道交通项目(JS-00-SG-17003).
张子凌(1994-), 男, 江苏淮安人, 在读硕士研究生, 主要研究方向: 冷弯钢冲击. E-mail: zzl969457093@163.com
朱珏(1979-), 女, 浙江金华人, 博士/教授, 主要研究方向: 冷弯钢结构. E-mail: zhujue@nbu.edu.cn
(责任编辑 章践立)
