基于线计算的全加器设计

李 林, 张跃军, 张会红

基于线计算的全加器设计

李 林, 张跃军*, 张会红

（宁波大学 信息科学与工程学院, 浙江 宁波 315211）

随着集成电路特征尺寸的不断缩小, 互连线在芯片内部占的比重越来越大, 但是互连线仅用于数据传输, 芯片计算能力仍然需要依靠晶体管开关实现. 如何在有限的硬件资源内进一步提高芯片的计算能力, 已经成为当前集成电路设计的核心问题. 本文通过研究金属互连线间电容耦合效应, 采用互连线串扰现象完成逻辑运算的思想, 提出一种基于线计算的全加器设计方案. 该方案首先建立线计算模型, 通过调整反相器阈值和不同干扰线与受扰线之间电容耦合强度匹配技术, 采用相同线计算电路结构实现不同功能的逻辑门电路; 然后, 在逻辑门的基础上实现基于线计算的全加器; 最后, 在TSMC 65nm CMOS工艺下仿真验证. 结果表明, 所设计的线计算电路具有正确逻辑功能, 与传统设计方法相比, 线计算逻辑门具有更低开销, 且线计算电路具有抗逆向工程能力.

线计算; 电容耦合; 门电路; 全加器

随着集成电路制造工艺技术的不断进步, 工艺尺寸进入纳米级, 芯片集成度增加, 系统性能提高, 但是互补金属氧化物半导体(Complementary Metal Oxide Semiconductor, CMOS)器件面临漏电流增大、可靠性和成品率低、制造成本增加等问题, 积极探索取代传统CMOS逻辑的设计方法已成为当前集成电路的研究热点[1-2]. 集成电路特征尺寸的减小, 互连线占用硬件开销越来越大, 且已经成为制约提高芯片计算能力的关键因素之一, 考虑将互连线作为逻辑计算的设计方法也引起了研究人员的广泛关注[3]. Macha等[4]从利用互连串扰效应角度出发, 提出使用互连线串扰进行计算的新概念, 以减少器件和互连规模来应对挑战. 线计算是利用纳米金属线间确定性干扰来实现逻辑运算的一种新型运算方式. 在线计算技术可扩展性方面, Iqbal等[5]利用互连线间的串扰来设计线计算电路, 展示对于最佳和最坏情况下的工艺变化, 且证明线计算电路都可正常工作. 在线计算应用方面, Desh等[6]提出基于线计算的新型模数转换(Analog to Digital Converter, ADC)概念, 通过仿真电路表明线计算ADC具有更低开销, 这为实现低功耗的ADC电路设计开辟了新的路径. Iqbal等[7]提出利用现有电子设计自动化工具流程进行大规模电路合成的关键方法, 为实现线计算电路与CMOS电路的兼容设计提供新的视角. 全加器是数字电路最基本的模块, 一直以来是集成电路的重点关注领域[8-9]. 目前, 国内外研究机构和高校设计多种不同逻辑风格的全加器单元, 它们分别在低功耗、低开销、高性能、高可靠等方面凸显优势[10-11].

本文通过研究互连线间电容耦合效应, 结合线计算电路设计原理, 在台积电(TSMC) 65nm CMOS工艺下采用相同电路结构实现3种线计算逻辑门, 提出基于线计算的全加器设计方案.

1 线计算理论分析与模型构建

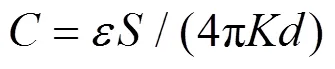
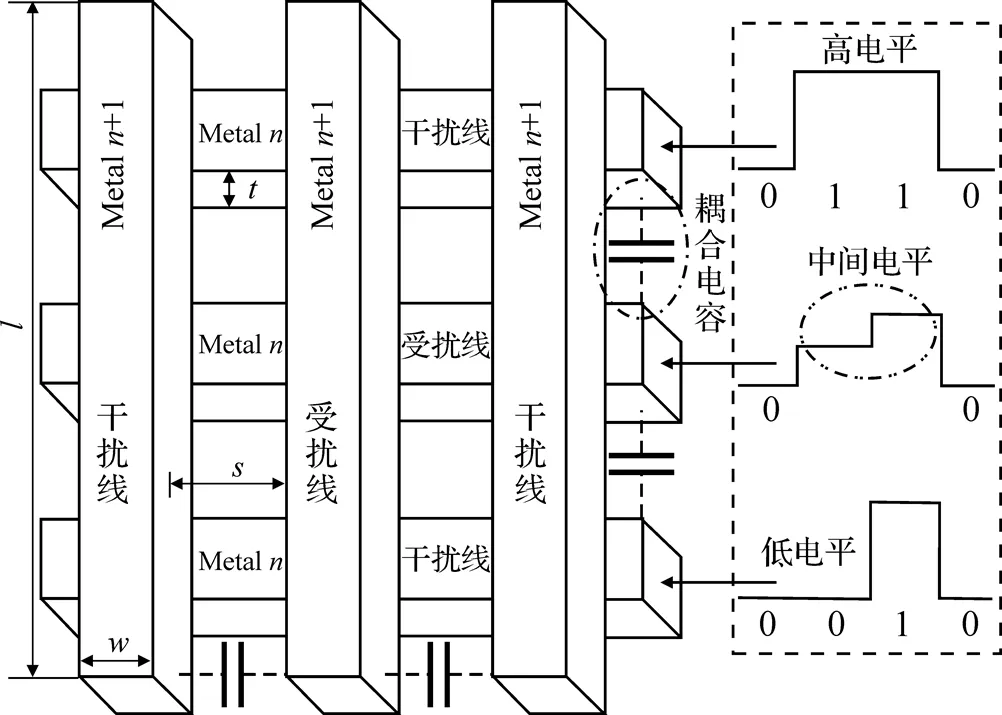
图1 线计算模型

2 线计算逻辑门设计

2.1 与门

线计算三输入与门版图如图2(b)所示, 电路中的耦合电容强度通过设置同层金属线之间的平行相对长度来实现, 即采用高层金属形成横向耦合电容, 其版图主要面积为2.484μm2.

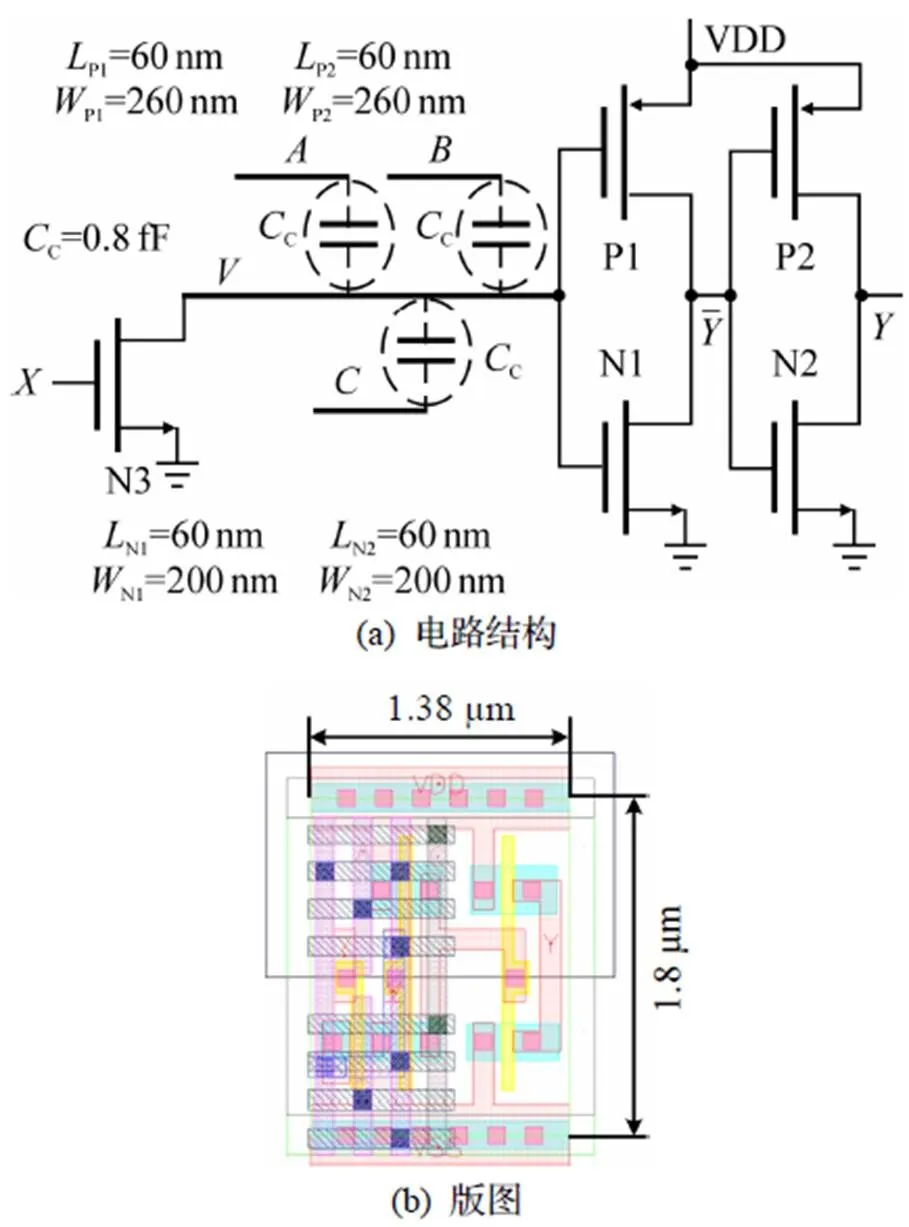
图2 三输入与门

2.2 复杂逻辑门

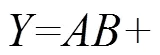
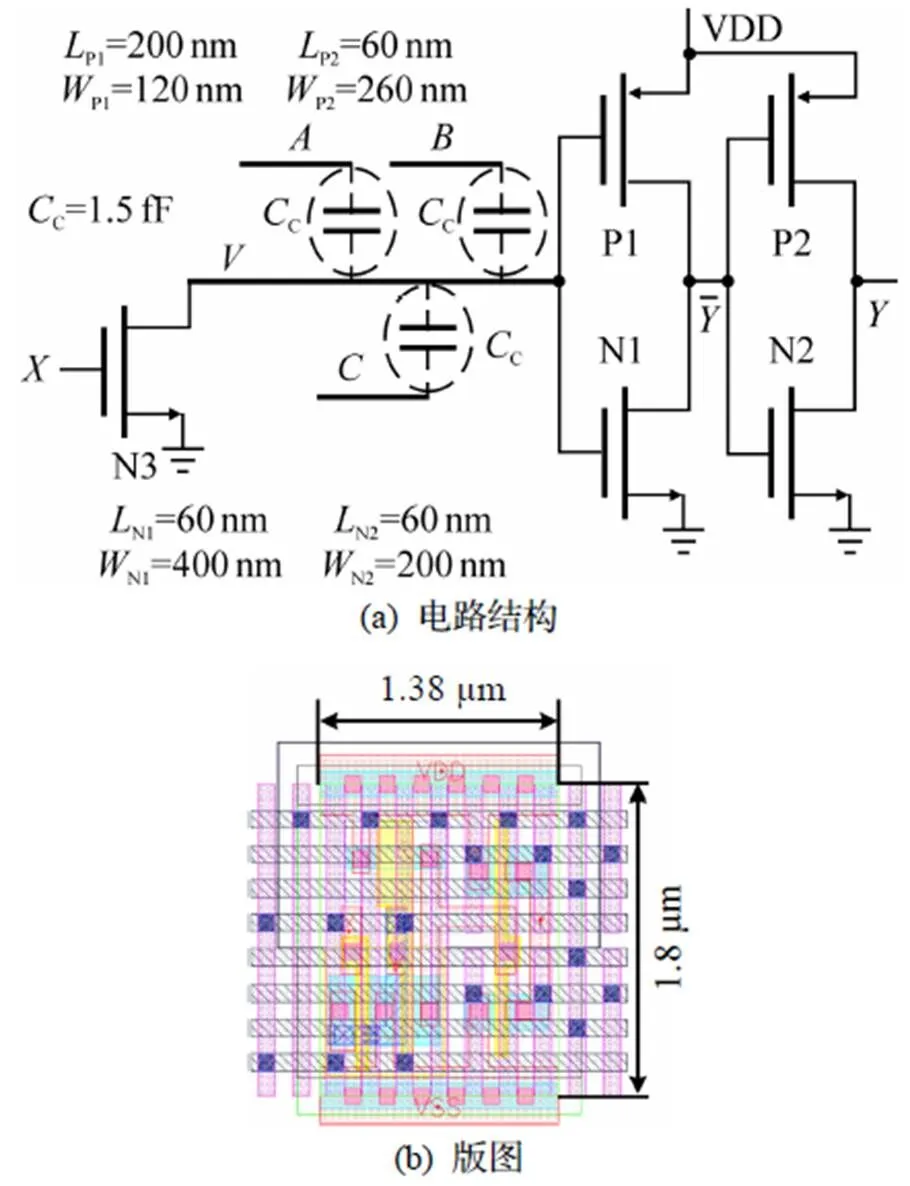
图3 三输入与或门

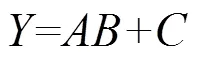
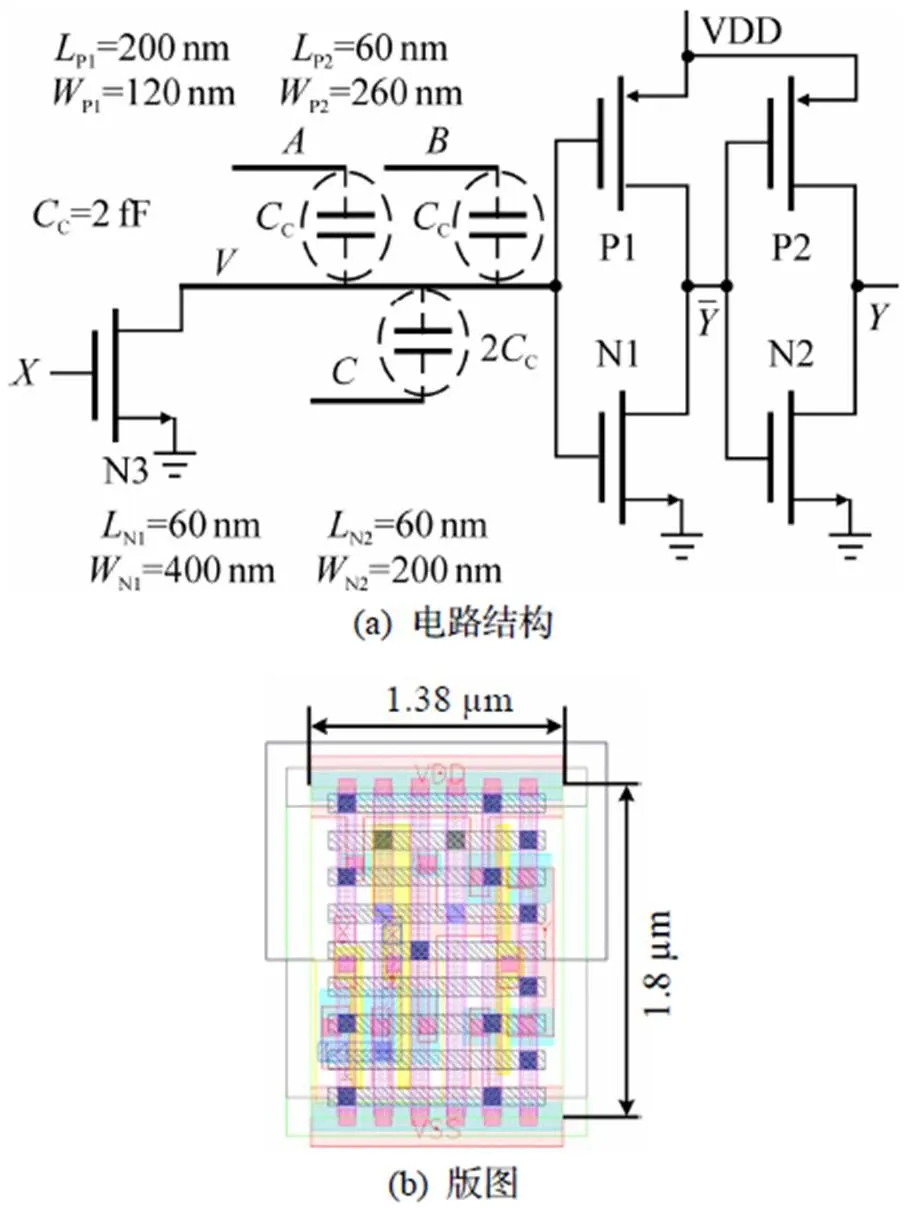
图4 Y=AB+C

3 全加器设计

3.1 一位全加器

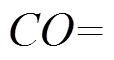
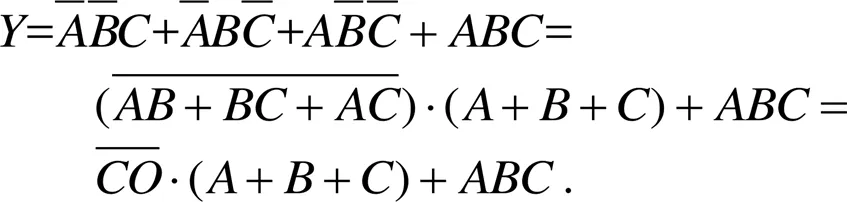
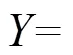
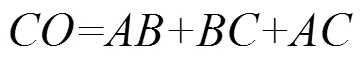
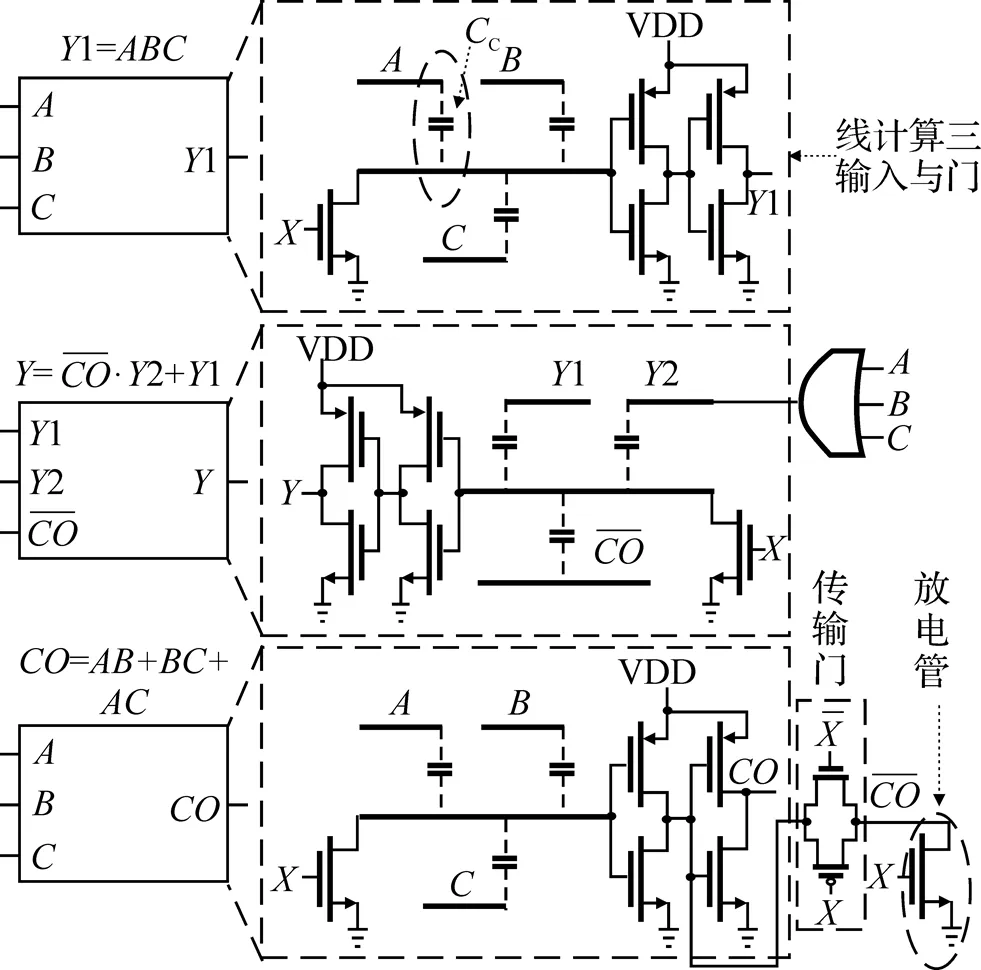
图5 一位全加器电路结构

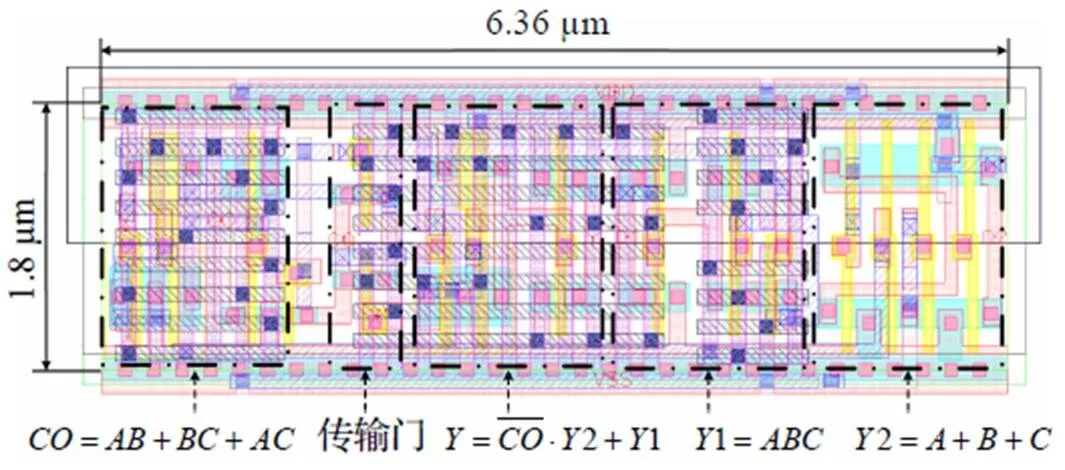
图6 一位全加器版图

3.2 多位全加器

将多个全加器级联起来, 上一个全加器的进位输出连接到下一个全加器的进位输入, 从而实现多位全加器. 线计算四位全加器电路结构如图7所示, 其版图如图8所示.

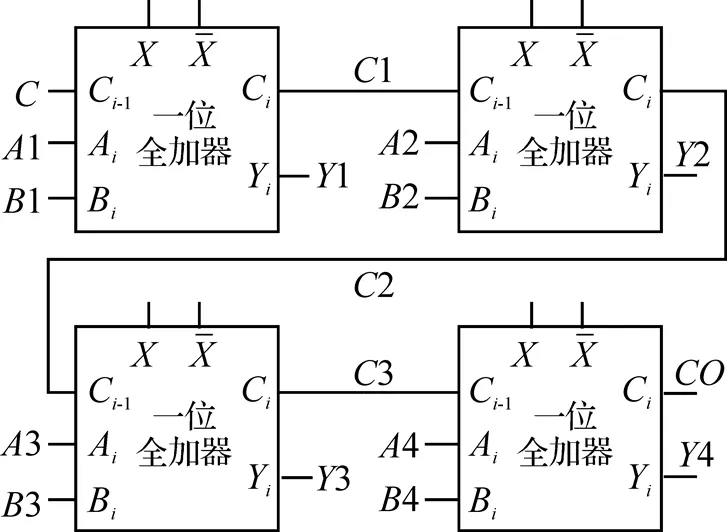
图7 四位全加器电路结构

图8 四位全加器版图

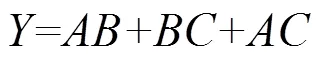
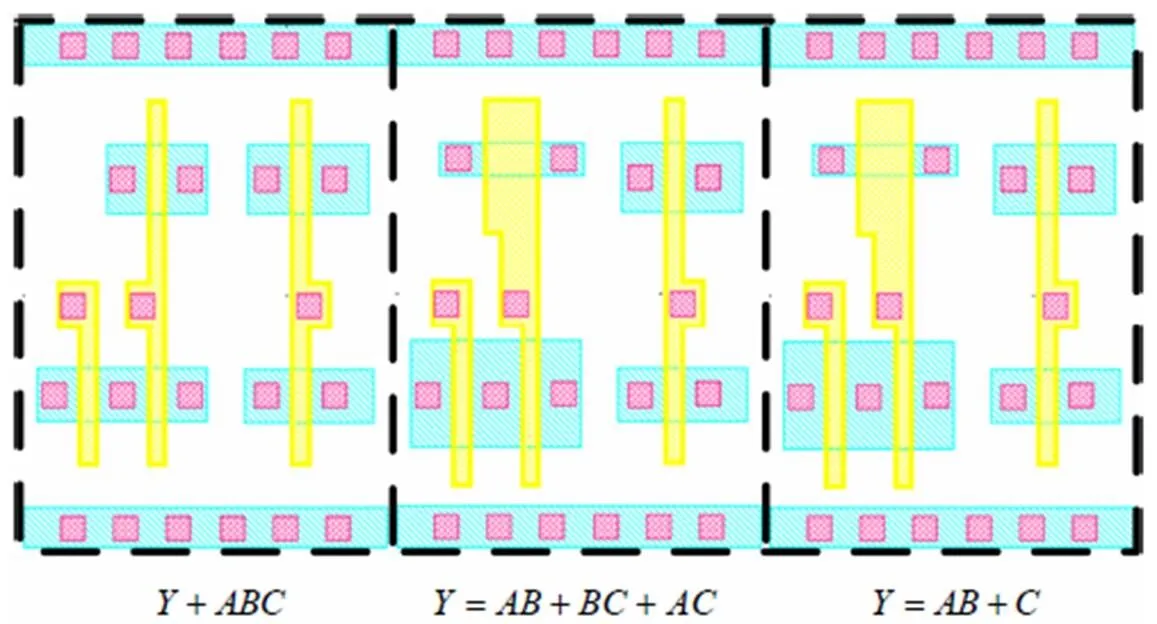
图9 有源区、多晶硅、接触孔布局图

4 实验结果与分析

4.1 与门仿真

在TSMC 65nm工艺下, 对线计算三输入与门进行功能验证, 仿真波形如图10所示. 线计算逻辑门工作状态有放电状态(Discharge State, DS)和求值状态(Evaluation State, ES)两种. 在0ns时刻,为高电平, 放电晶体管NMOS导通至地, 电路工作在放电状态, 受扰线放电为逻辑0. 在1ns时刻,为低电平, 放电管不导通, 电路工作在求值状态, 干扰线为逻辑0, 干扰线和干扰线从逻辑0跃变为逻辑1, 经耦合电容的感应作用, 受扰线产生0.48V电压信号, 经两级反相器整形输出为逻辑0. 同理, 在3ns时刻, 干扰线和干扰线从逻辑0跃变为逻辑1, 受扰线也产生0.48V电压信号, 从而输出为逻辑0. 在5ns时刻, 干扰线和干扰线都为逻辑0, 仅干扰线从逻辑0跃变为逻辑1, 经耦合电容的感应作用, 受扰线仅产生0.22V电压信号, 经两级反相器整形输出为逻辑0. 在7ns时刻, 干扰线、和均从逻辑0跃变为逻辑1, 经耦合电容的感应作用, 受扰线产生的耦合电压最高, 其值为0.7V, 经两级反相器整形输出为逻辑1. 仿真线计算三输入与门在不同负载下的功耗和延时情况, 输出端后接4个并联的反相器作为负载, 负载输出端为1; 输出端后接8个并联的反相器作为负载, 负载输出端为2. 当负载为4个并联的反相器时, 电路平均功耗为2.62μW, 输出端1的平均延时为85ps. 当负载为8个并联的反相器时, 电路平均功耗为3.75μW, 输出端2的平均延时为112ps.

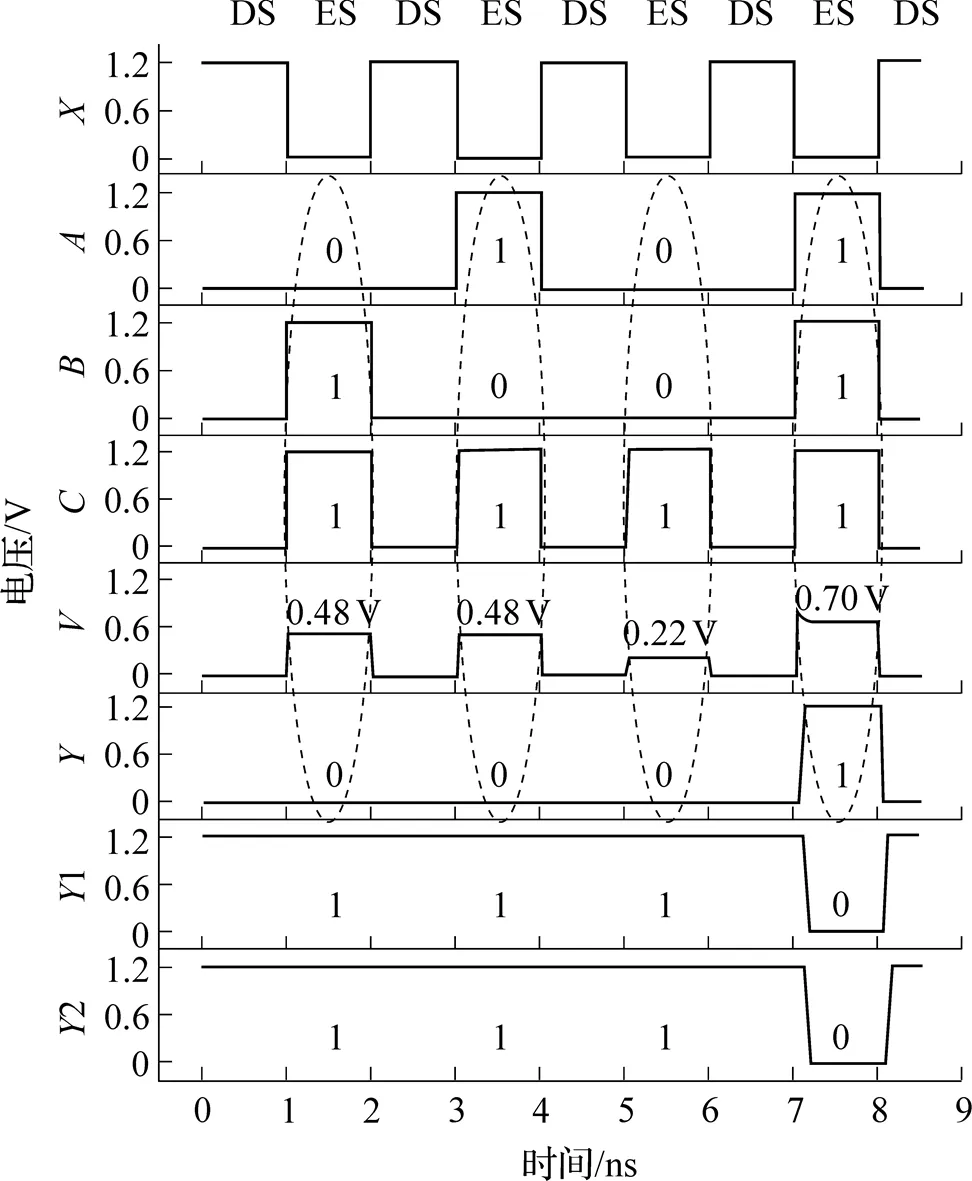
图10 三输入与门仿真波形

4.2 复杂逻辑门仿真

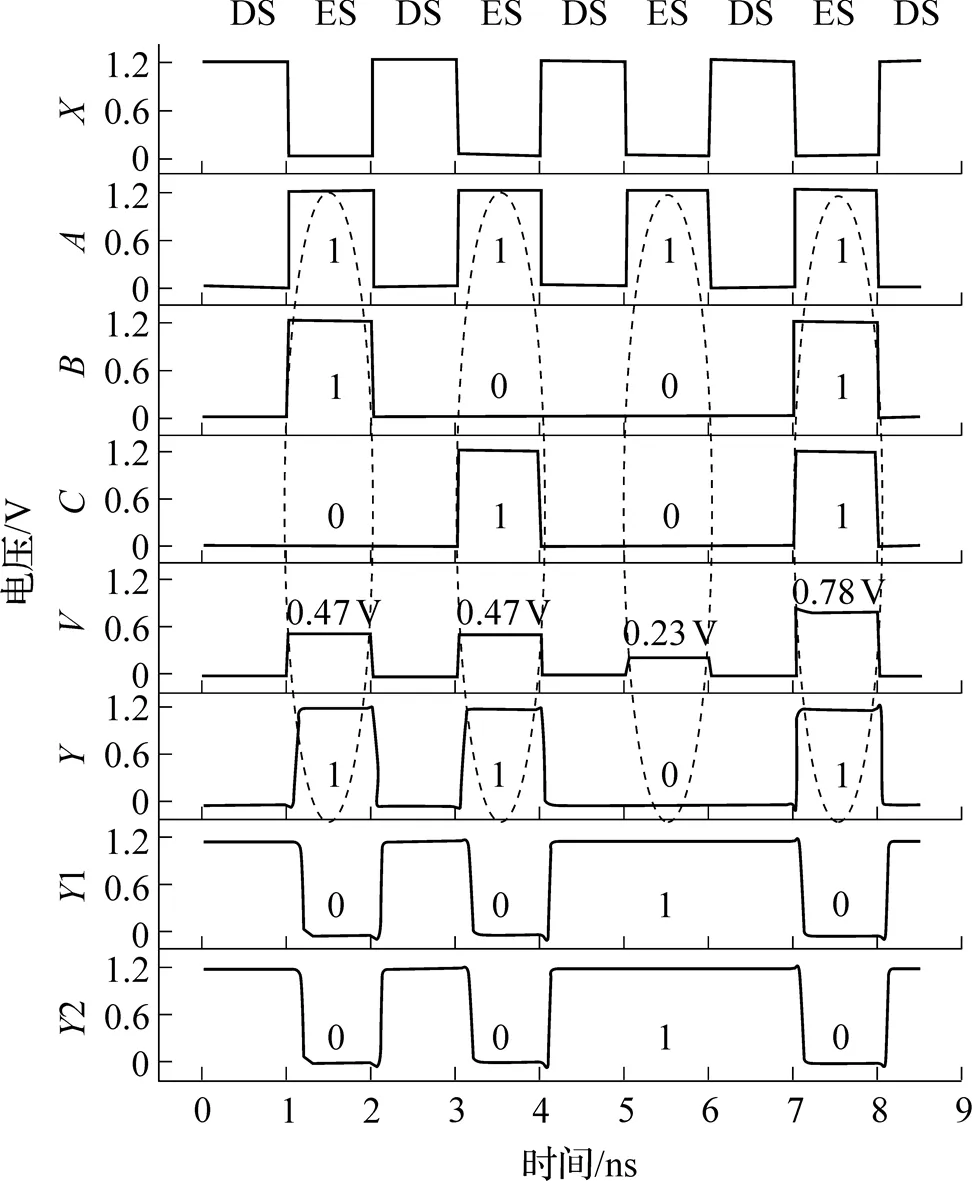
图11 Y=AB+BC+AC逻辑门仿真波形

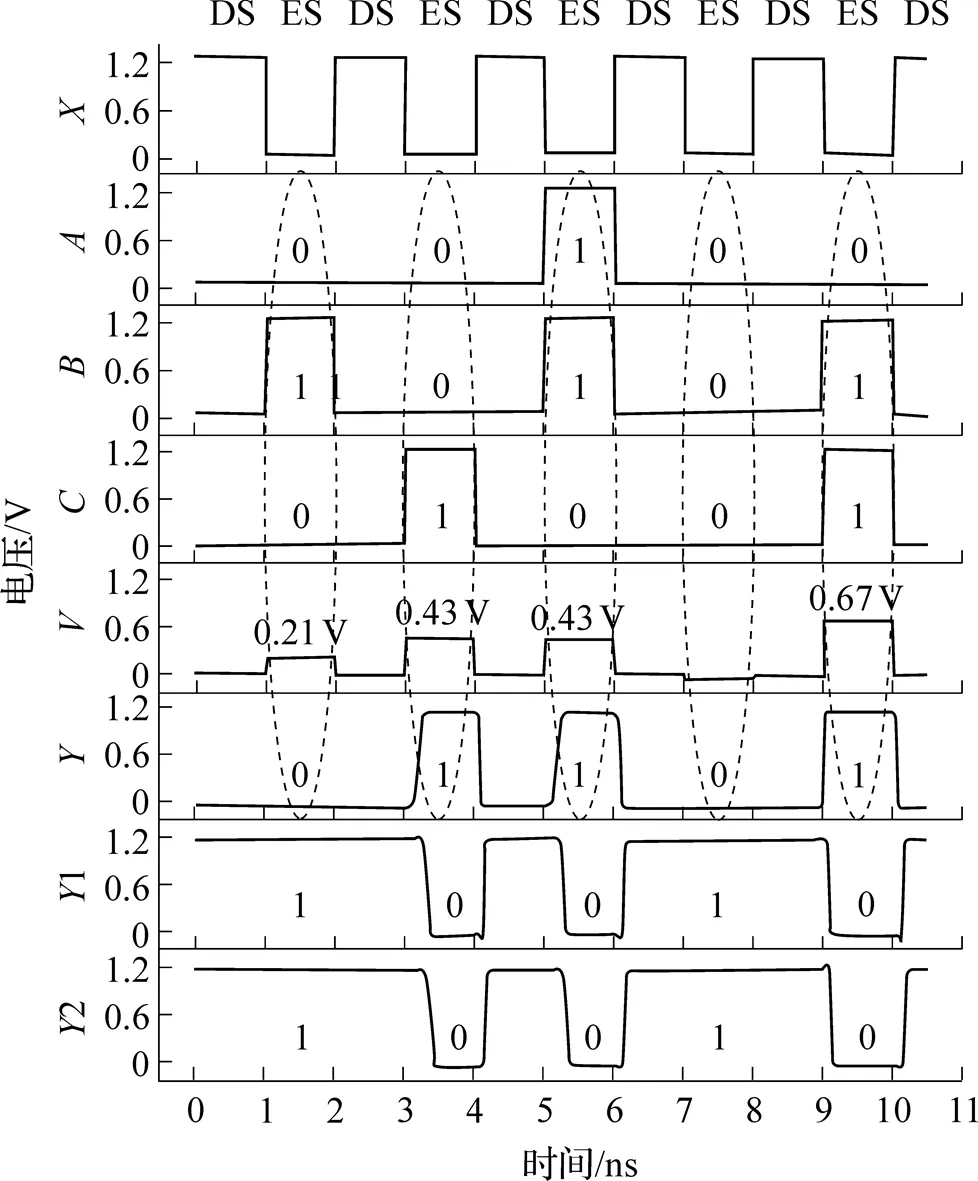
图12 Y=AB+C逻辑门仿真波形

4.3 全加器仿真

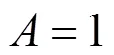
进一步对线计算四位全加器版图提取寄生参数进行后仿真, 其仿真波形如图14所示. 电路求值前, 受扰线电压清零, 使得干扰线从逻辑0到逻辑1跃变时, 在受扰线上能产生感应电压. 在1ns时刻, 输入被加数[4:1]=1011、加数[4:1]=1010、低位进位=0, 输出4321=0101、=1. 在3 ns时刻, 输入被加数[4:1]=1101、加数[4:1]= 1100、低位进位=1, 输出4321=1010、=1. 在5ns时刻, 输入被加数[4:1]=1001、加数[4:1]= 1000、低位进位=0, 输出4321=0001、=1. 在15ns时刻, 输入被加数[4:1]=1111、加数[4: 1]=1111、低位进位=1, 输出4321=1111、= 1. 仿真结果表明, 基于线计算的四位全加器逻辑功能正确.

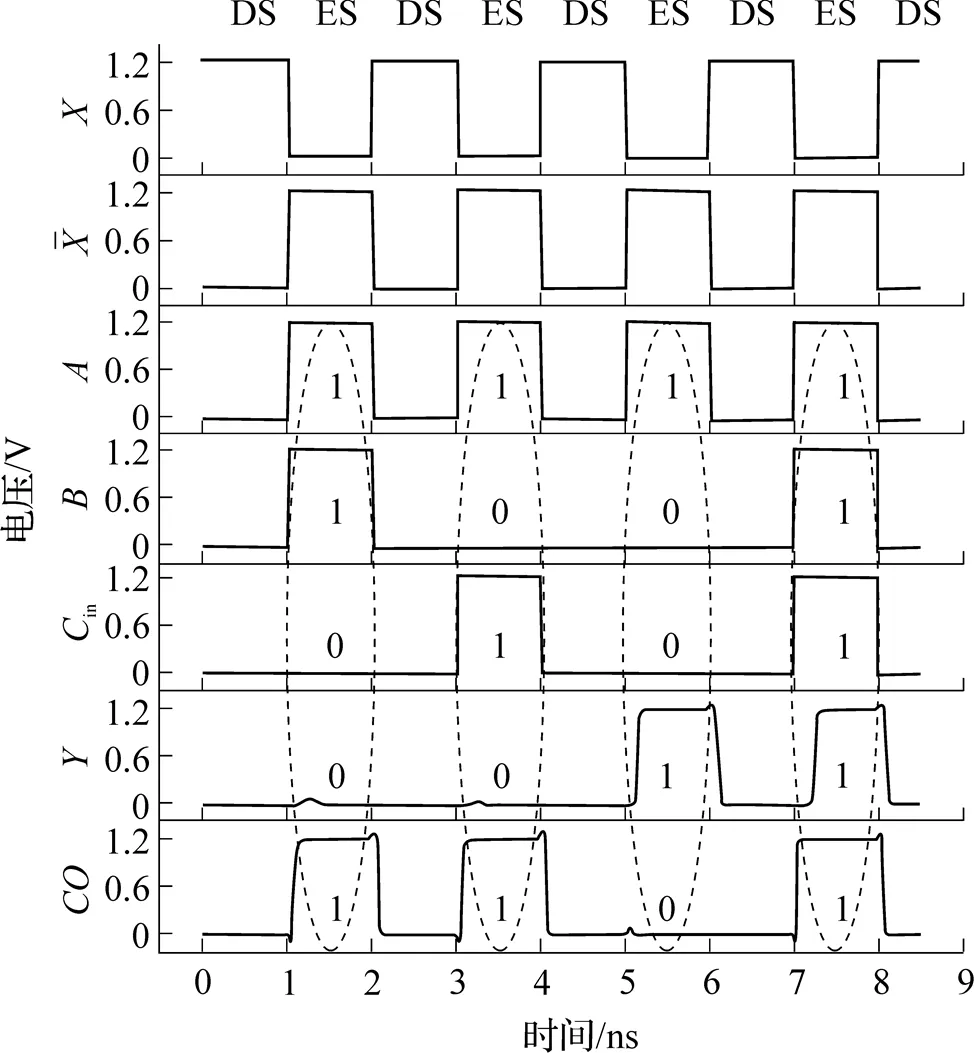
图13 一位全加器仿真波形

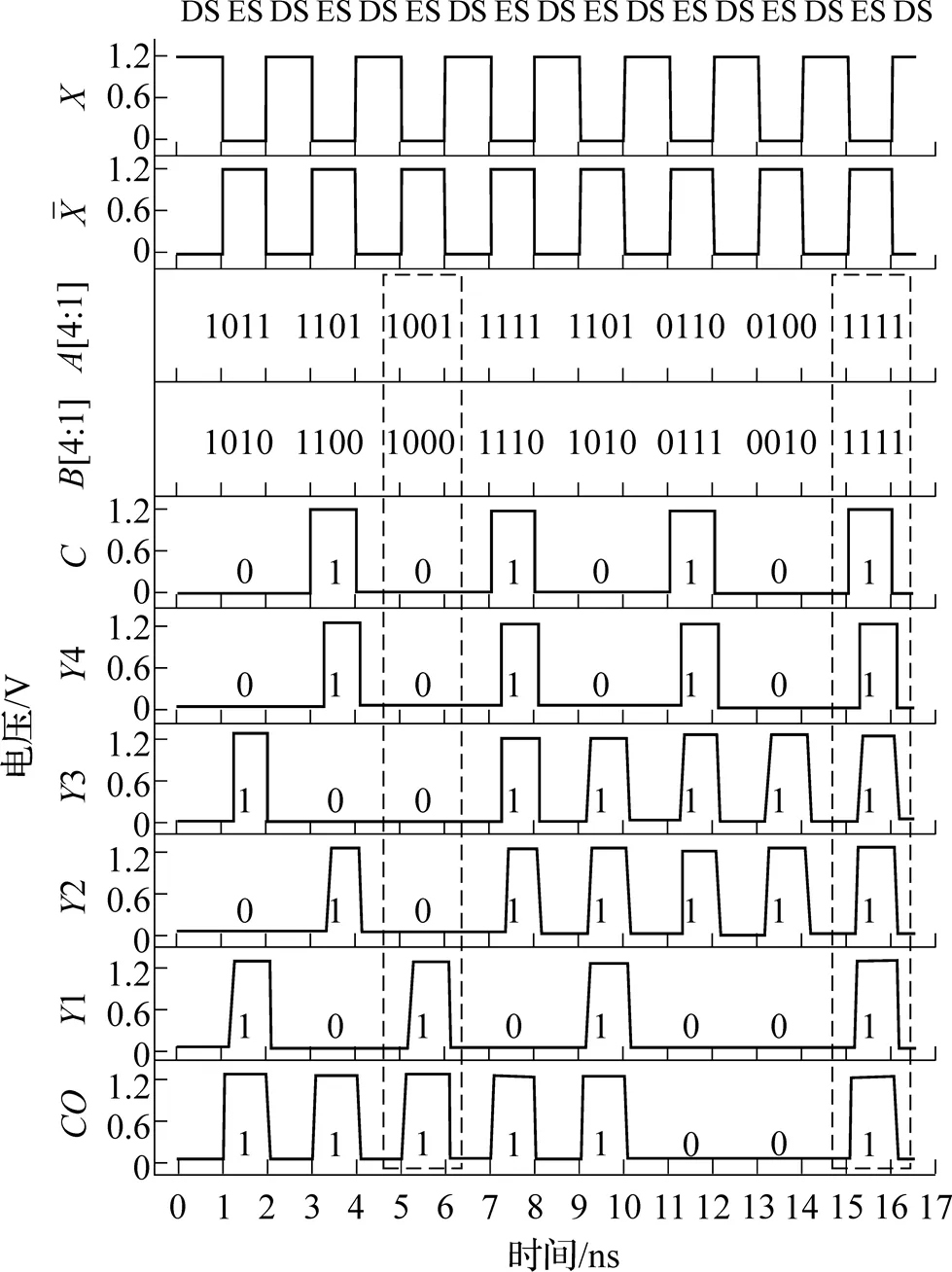
图14 四位全加器仿真波形

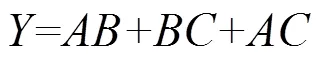
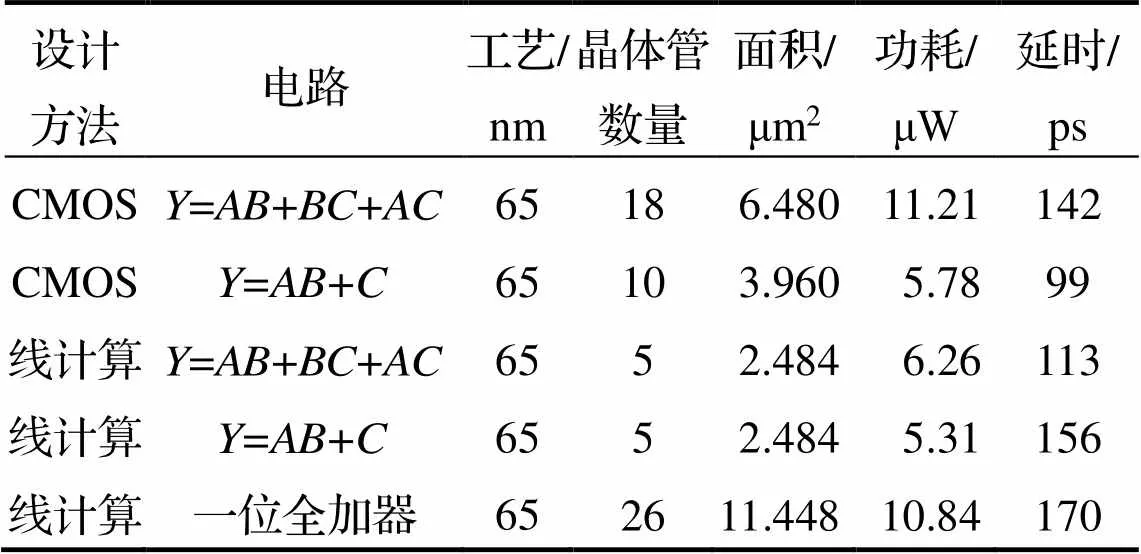
表1 与相关设计电路比较

5 结论

通过对线计算理论和模型的研究, 探索采用相同电路结构实现不同逻辑功能, 提出一种基于线计算的全加器设计方案. 在TSMC 65nm CMOS工艺下, 采用全定制方式完成了线计算与门和复杂逻辑门, 并继而实现线计算一位全加器和四位全加器, 仿真验证所设计的线计算电路具有正确的逻辑功能. 同时, 所设计的线计算全加器电路结构中包含多个相同结构的不同逻辑功能的相似伪装门, 使其具有抗逆向工程能力, 可广泛应用于安全芯片中, 对提高集成电路抗逆向工程的能力具有重要意义.

[1] Kim N S, Austin T, Baauw D, et al. Leakage current: Moore’s law meets static power[J]. Computer, 2003, 36(12):68-75.

[2] Kim, Y B. Challenges for nanoscale MOSFETs and emerging nanoelectronics[J]. Transactions on Electrical and Electronic Materials, 2010, 11(3):93-105.

[3] Ullah M S, Chowdhury M H. Analytical models of high speed RLC interconnect delay for complex and real poles[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2017, 25(6):1831-1841.

[4] Macha N K, Chitturi V, Vijjapuram R, et al. A new concept for computing using interconnect crosstalks[C]// IEEE International Conference on Rebooting Computing, Washington DC, USA, 2017:1-2.

[5] Iqbal M A, Macha N K, Repalle B T, et al. Designing crosstalk circuits at 7nm[C]//IEEE International Conference on Rebooting Computing, San Mateo, CA, USA, 2019:1-4.

[6] Desh R, Macha N K, Hossain S, et al. A novel analog to digital conversion concept with crosstalk computing[C]// IEEE/ACM International Symposium on Nanoscale Architectures, Athens, Greece, 2018:1-3.

[7] Iqbal M A, Macha N K, Repalle B T, et al. A logic simplification approach for very large scale crosstalk circuit designs[C]//IEEE/ACM International Symposium on Nanoscale Architectures (NANOARCH), Qingdao, China, 2019:1-6.

[8] Goel S, Kumar A, Bayoumi M A. Design of robust, energy-efficient full adders for deep-submicrometer design using hybrid-CMOS logic style[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2006, 14(12):1309-1321.

[9] Bhattacharyya P, Kundu B, Ghosh S, et al. Performance analysis of a low-power high-speed hybrid 1-bit full adder circuit[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2015, 23(10):2001-2008.

[10] Gang Y, Zhao W S, Klein J O, et al. A high-reliability, low-power magnetic full adder[J]. IEEE Transactions on Magnetics, 2011, 47(11):4611-4616.

[11] Amirany A, Rajaei R. Fully nonvolatile and low power full adder based on spin transfer torque magnetic tunnel junction with spin-hall effect assistance[J]. IEEE Transactions on Magnetics, 2018, 54(12):1-7.

Design of full adder based on line crosstalk computing

LI Lin, ZHANG Yuejun*, ZHANG Huihong

( Faculty of Electrical Engineering and Computer Science, Ningbo University, Ningbo 315211, China )

With the on-going reduction of the characteristic size of integrated circuits, the interconnected metal wires take up an increasing proportion in the chip space. However, these wires are only used for data transmission, and the chip’s computing ability still depends on the switch of transistors. How to improve the computing ability of chip with limited hardware resources has become a key issue of IC design. In this paper, by studying the capacitive coupling effect resulting from the metal interconnectors and the advantage of using the line crosstalk phenomenon to complete the logical operation, a design scheme of full adder based on line crosstalk computing is proposed. The scheme first establishes a line crosstalk computing model, and uses the same line crosstalk computing circuit structure to implement different logic gates by adjusting the inverter threshold and the capacitive coupling strength between different interference lines and the victim line. Then, a full adder based on line crosstalk computing is implemented on the basis of logic gates. Finally, the simulation verification under the TSMC 65nm CMOS process shows that the designed line crosstalk computing circuit has the correct logic function. Compared with traditional design methods, the line crosstalk computing logic gates achieve lower overhead, and the line crosstalk computing full adder acquires the ability to resist reverse engineering scheme.

line crosstalk computing; capacitive coupling; logic gate; full adder

TP331

A

1001-5132（2022）01-0040-08

2021−07−29.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

国家自然科学基金（61871244, 61874078）; 浙江省省属高校基本科研业务费专项资金（SJLY2020015）; 宁波市公益性计划项目（202002N3134）; 宁波市科技计划项目（202003N4107）; 宁波大学研究生科研创新基金（IF2021158）.

李林（1997－）, 男, 湖南岳阳人, 在读硕士研究生, 主要研究方向: 线计算逻辑电路设计. E-mail: lilin20211@163.com

张跃军（1982－）, 男, 浙江台州人, 副教授, 主要研究方向: 信息安全芯片与低功耗集成电路设计. E-mail: zhangyuejun@nbu.edu.cn

（责任编辑 章践立）