一类p规范型非线性系统预设性能有限时间H∞跟踪控制

李小华 胡利耀

近几年,凭借快速的收敛性和较强的鲁棒性,有限时间控制方法已经成为控制理论研究的热点[1-4],并且已经获得了许多的研究成果[5-9].其中,有一类文献针对有限时间跟踪控制问题进行了研究[6-9].文献[6]针对一个五阶移动机器人系统采用Backstepping技术设计了系统的有限时间跟踪控制器,使得系统的跟踪误差在有限时间内收敛到平衡点;文献[7] 利用加幂积分技术,研究了空间飞行器的有限时间跟踪控制问题;在文献 [8]中,作者利用齐次域方法,解决了四旋翼飞行器的有限时间跟踪控制问题.但是对于p规范型非线性系统,很少有文章研究其有限时间跟踪控制问题.经查找仅有文献 [9]结合加幂积分技术和凸组合方法,针对一类切换p规范型非线性系统设计了一个状态反馈跟踪控制器,该跟踪控制器能够保证系统的跟踪误差在有限时间内收敛到平衡点的小的邻域内.但是上述方法均不能保证系统跟踪误差的整个暂态过程被限制在一个给定的范围内,而跟踪误差波动太大对实际系统而有一定风险的.并且,大多数文献中的系统停息时间均与初始状态有关.

因为预设性能控制方法能够同时兼顾到系统的暂态和稳态性能[10],所以国内外许多专家学者对此进行了大量的研究[11-13].然而,目前大多数关于预设性能的控制方法均存在一个共性问题,即在对系统进行误差转换时已设定了该误差的有界性,然后再去证明它的有界性[10-13],这是不合理的.而文献 [14]提出一种新的误差转换函数,在解决预设性能控制问题时不需要提前设定误差的有界性,从而避免了该共性问题.但该方法只能保证系统在t→∞时系统状态误差收敛到平衡点的一个小的邻域内,对于解决一类对收敛时间要求较高的控制问题时不太理想.为此,文献 [15] 将预设性能控制方法和有限时间控制方法相结合,提出了一种有限时间性能函数,并利用所提出的性能函数,设计了一类非严格反馈非线性系统的有限时间跟踪控制器,该控制器能够保证系统的跟踪误差在任意给定的时间内收敛到平衡点的一个预先给定的邻域内,并且停息时间与系统的初始状态无关.然而,该设计方法仍然存在预设性能的共性问题.并且文献 [14-15]只考虑了系统的幂p=1的情况.而我们知道,许多实际的系统是p规范型形式的非线性系统,其系统的幂p/=1,例如欠驱动弱耦合的机械系统[16]等等,文献[14-15]给出的方法不能直接用于这类p规范型系统中,且它们也没有考虑外部扰动对系统的影响.

对于系统的外部扰动可以采用H∞控制方法来抑制其影响.该方面的成果已有许多[17-22].其中有一些成果是针对于非线性系统的H∞控制问题[19-22].特别有文献 [22]对一类严格反馈非线性系统设计了有限时间H∞控制器,但该H∞控制器是在系统为渐近稳定的前提下得到的,对于只能满足有界稳定的系统,该设计方法是失效的.应该说明的是,目前还没有关于p规范型非线性系统的H∞控制的研究报道.

本文基于预设性能控制方法,结合加幂积分技术、H∞控制方法以及神经网络自适应技术,针对于一类带有外部扰动的非严格反馈p规范型非线性系统设计了一个自适应神经预设性能有限时间H∞控制器,该控制器能够保证被控系统的跟踪误差在任意给定的停息时间内收敛到平衡点的一个预先给定的邻域内,系统是实际有限时间稳定的,并且跟踪误差始终在有限时间性能函数约束的范围内,同时外部扰动对系统的影响能够被抑制.

本文的主要贡献为:1)首次考虑了一类带有外部扰动的非严格反馈p规范型非线性系统的预设性能有限时间H∞控制问题,并且首次将有限时间性能函数和加幂积分器技术相结合;2)由于外部扰动及系统的高次幂的影响,文献 [14]中所提出的预设性能方法并不能直接应用.为了避免预设性能控制方法存在的共性问题,本文基于文献 [14]中的思想,提出一种新的预设性能控制器的设计方法.该方法亦避免了该共性问题;3)不同于文献[22],本文解决了非线性系统为有界稳定时设计H∞控制器的困难;4)与文献[14-15]相比,系统的幂p被放宽到奇整数之比的形式;并且考虑了系统带有外部扰动的情况.

1 问题描述和预备知识

1.1 系统描述

本文考虑如下一类非严格反馈p规范型非线性系统:

其中,x=[x1,···,xn]T∈Rn为系统的状态向量;y ∈R是系统的输出;u∈R为系统控制输入.gi(x),fi(x)和φi(x)为未知的C1函数;wi(t)∈L2[0,T] 为非零外部扰动;系统的幂pi≥1 为两个奇整数之比的形式.该系统满足如下假设:

假设 1.系统(1)中函数gi(x)(i=1,2,···,n)的函数符号已知,并且存在未知正常数b使得b≤|gi(x)|＜∞.不失一般性,假设gi(x)＞0.因此b≤gi(x)＜∞.

本文考虑系统的跟踪控制,要求被跟踪信号yd(t)满足:

假设 2.被跟踪的信号yd(t)及其k阶导数连续且有界,k=1,2,···,n.

1.2 预备知识

为了得到主要的结果,下面给出一些有用的引理与定义.

引理1[19].对于任意的实数ε＞0,下面不等式成立:

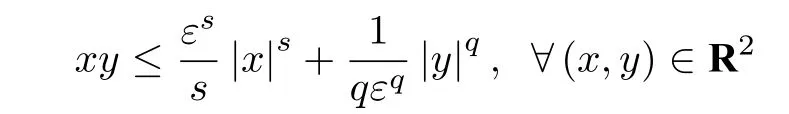
其中,常数s＞1,q＞1 并且满足(s-1)(q-1)=1.

引理2[23].对于xi,i=1,···,n和实数 0＜ℓ ＜1,有下面的不等式成立:

若 0＜ℓ=ℓ1/ℓ2≤1,其中ℓ1＞0和ℓ2＞0 均为奇整数,则

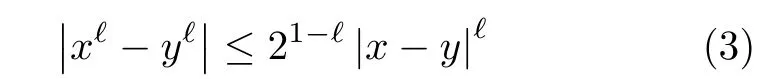
其中,x和y为任意实数.

在本文中,采用径向基函数神经网络 (Radial basis function neural network,RBFNN)在线逼近未知非线性函数f(Z).即

其中,σi为基函数的中心,κi为高斯函数的宽度.我们知道,只要采用足够多的节点数l,RBFNN 能够逼近在紧集Ω⊂Rm上的任意连续函数f(Z)[24].即

其中,ϑ*T为理想的常数权向量,定义为

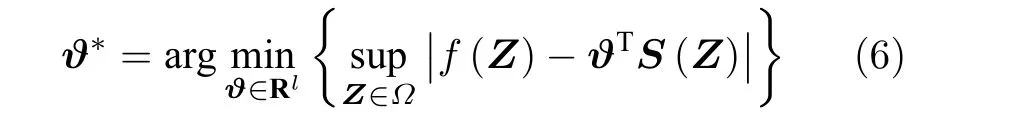
δ(Z)是逼近误差且满足|δ|≤δ*,其中,δ*为有界正常数.

引理3[25].对于任意的正整数r,n及神经网络中的基函数S(Z)=[s1(Z),···,sl(Z)]T,不等式 (7)成立.

其中,=[z1,···,zn]T和Zr=[z1,···,zr]T为输入向量.

引理4 (Gronwall 不等式)[26].假 设x(t),F(t)和χ(t)≥0是定义在t∈[a,b] 上的连续实值函数.如果不等式

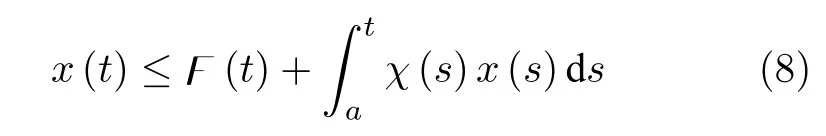
成立,则有

定义1[15].考虑以下非线性系统

其中,x是状态向量;h(x):Ω→Rn是一个在原点的开邻域 Ω 上连续的函数,并且满足h(0)=0.如果当t ≥T(x0)时,对任意的初始条件x(0)=x0都有‖x‖≤ϵ,其中ϵ ＞0是一个常数,0＜T(x0)＜∞表示该系统的停息时间.则系统 (10)是实际有限时间稳定的.

注1.本文的停息时间与系统初始状态无关.

定义2.对于非线性系统(1),如果满足:1)对于任意的初始状态,存在一个Lyapunov函数V＞0满足≤-ζV+;2)不等式 (11)成立

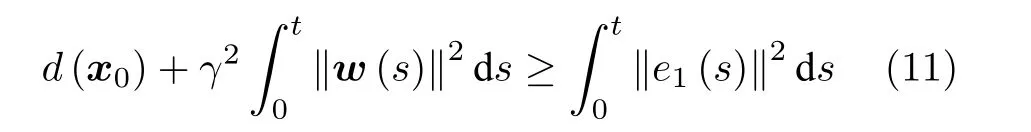
则称系统 (1)满足有界H∞性能指标.其中,ζ,Θ¯均为正实数;e1(t)=y(t)-yd(t)表示系统跟踪误差,d(x0)是一个正数,w(t)∈L2[0,T] 是非零外部扰动,γ为给定的干扰抑制系数.

定义 3[15].如果光滑函数α(t)满足:1)α(t)＞0;2)(t)≤0;3)limt→Tfα(t)=αTf;4)当t≥Tf时,α(t)=αTf,则称其为有限时间性能函数,其中,αTf和Tf为任意的正实数.

在本文中,有限时间性能函数被选择为

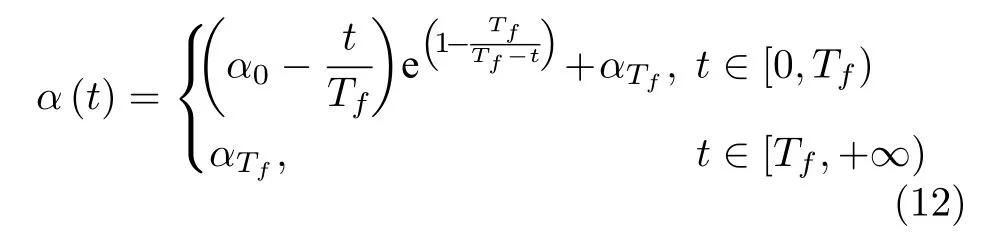
其中,α0≥1,αTf＞0和Tf＞0均为设计参数.并且α(t)的初始值为α(0)=α0+αTf.易知,该有限时间性能函数(12)满足定义3.其光滑性的证明见文献[15].

这里借用文献[14]中的思想定义误差转换函数为

本文的控制目标为:针对p规范型非线性系统 (1)设计一个自适应神经预设性能有限时间H∞跟踪控制器,使得当|e1(0)|＜α(0)时,该控制器能够保证系统的跟踪误差e1(t)=y(t)-yd(t)被约束在有限时间性能函数(-α(t),α(t))内,并能够在任意给定的停息时间内收敛到平衡点附近预先给定的邻域内,且闭环系统 (1)的所有信号是实际有限时间稳定的;外部扰动对系统性能的影响能够得到抑制.

为了简化推导过程,本文将函数gi(x),fi(x),φi(x),wi(t)以及一些相关的函数简写为gi,fi,φi,wi.

2 主要结果

下面将根据控制目标对系统 (1)设计一个自适应神经预设性能有限时间H∞跟踪控制器.

首先,给出一系列坐标变换

第1步.选择Lyapunov 函数为

其中,β1＞0 为设计参数.考虑式 (13)和式 (14),对V1求导,可得

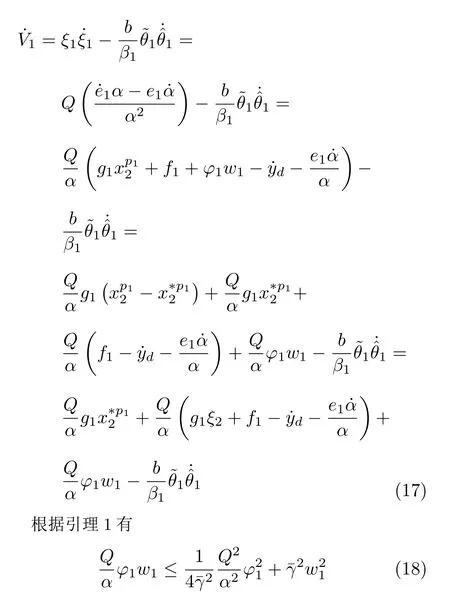
因为函数 Φ1中包含有未知连续函数,所以这里使用神经网络对其进行估计.根据式 (5),有

利用引理1 和引理3,有

λ1＞0为设计参数.

将式 (21)代入式 (19)并整理,有

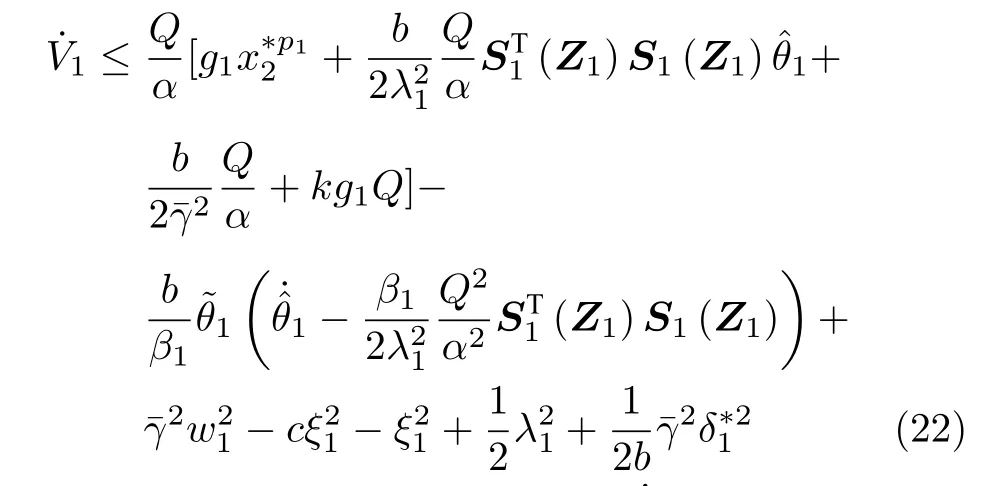
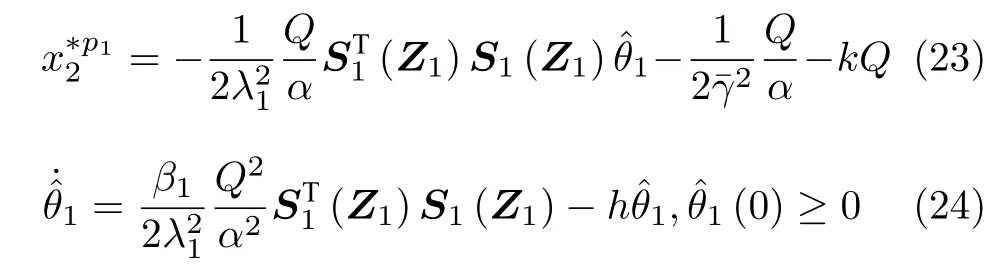
其中,h＞0 是一个设计参数.则式 (22)能够改写为

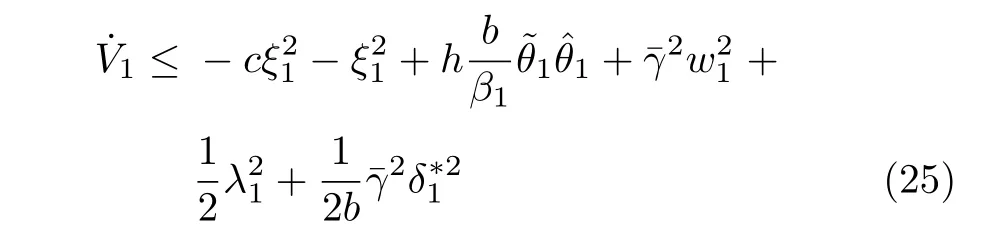
为了使后面的推导更易于表达,将式(16)改写为

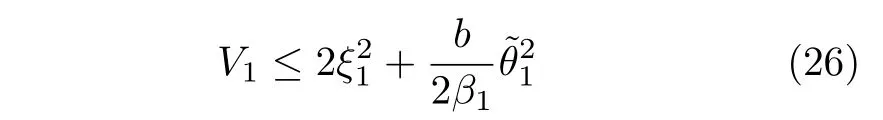
第i(2≤i ≤n-1)步.选择Lyapunov 函数为

βi＞0为设计参数.

根据式 (14),式 (27),式 (28)及引理2,易有式 (29)～(34)成立.

因为式 (30)～(34)的证明过程是容易的,限于篇幅,此处省略.

根据引理2 与式 (14),有

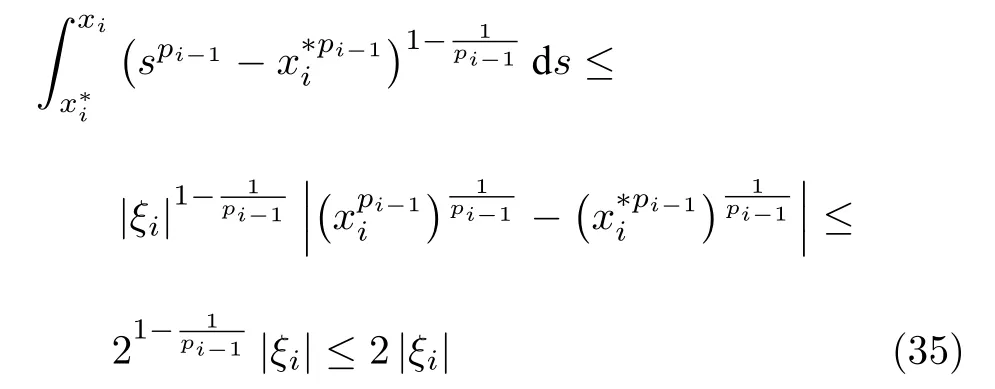
因此,式 (31)～(34)能够改写为

下面分别对式 (40)中一些项进行处理.根据式 (36)及引理1,易得

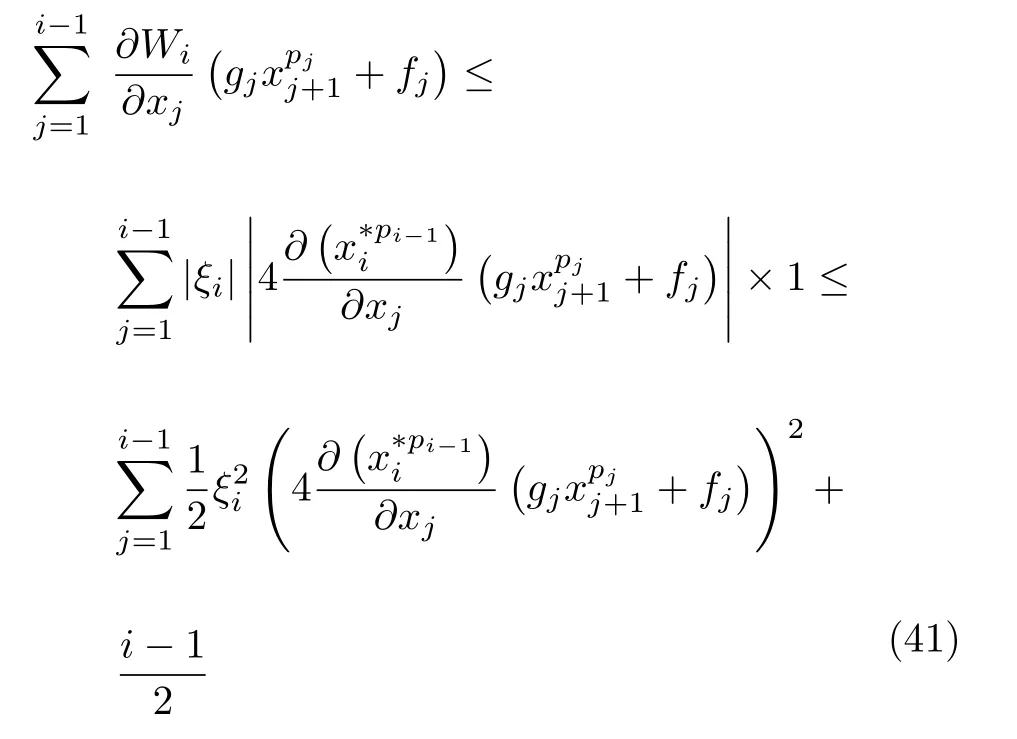
类似地,根据式(37)～(39)及引理1,可得

将式 (41)～(45)代入式 (40)并整理,有

因为 Φi为未知连续函数,所以利用神经网络对其进行估计.类似于式 (20)和式 (21),利用引理1、引理3 和式 (5),有

λi＞0为设计参数.

将式 (47)代入式 (46),有

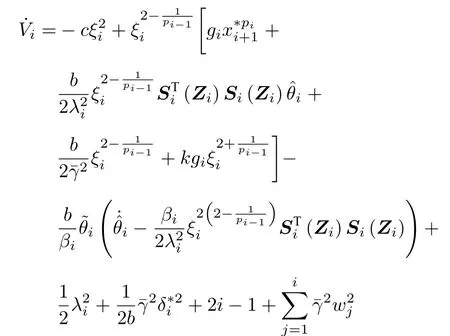
第n步.选择新的Lyapunov 函数为

其中,

βn＞0为设计参数;ε ＞0 为实数.

注 2.特别地,在Lyapunov 函数选择中加入ε是为了确保Vn＞0恒成立,其目的是为了便于证明H∞性能指标.它只是一个辅助参数,并不参与最终控制器的设计,因此其具体值并不需要知道.

类似于第i步,有

因为 Φn中包含未知项,根据引理1,可得

其中,λn＞0 为设计参数.

将式 (55)代入式 (54)并整理,式 (54)能够改写为

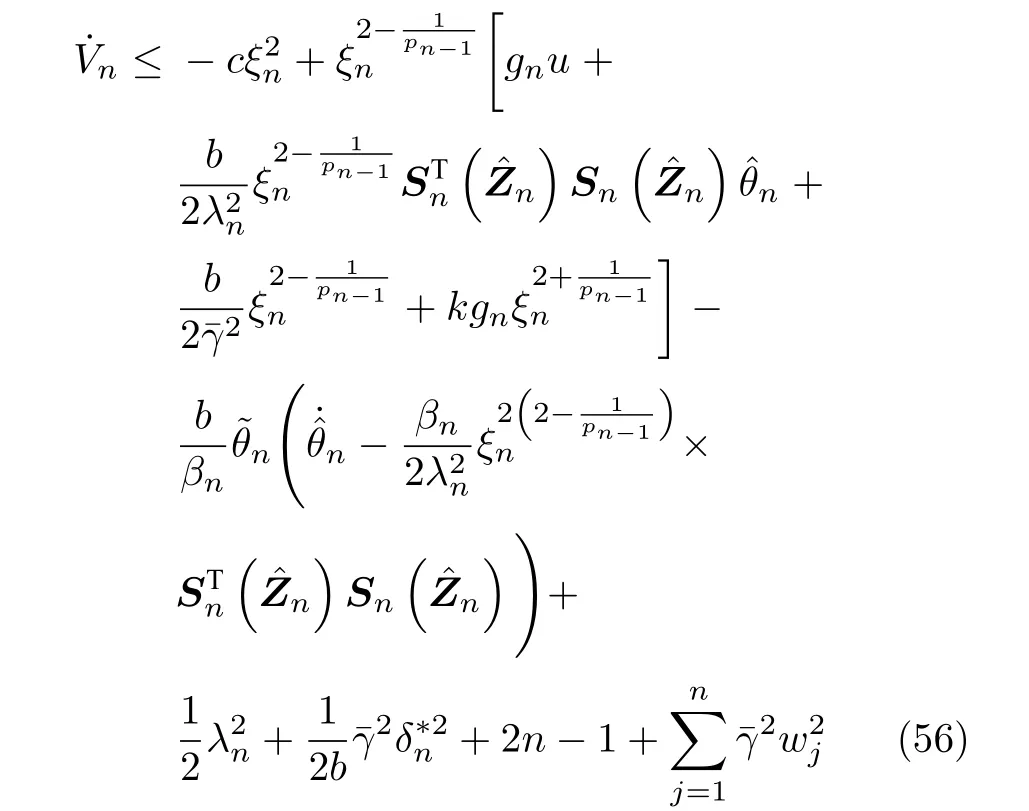
由此可得最终的控制律u和自适应律为

至此,本文的主要结果可给出如下:

定理1.对于满足假设1 和假设2 的p规范型非线性系统 (1),如果初始条件满足|e1(0)|＜α(0),并且控制律和自适应律按照式 (23),(48),(57)和式 (24),(49),(58)来选取,则系统 (1)满足:1)跟踪误差e1(t)能够被预先给定的有限时间性能函数α(t)约束,且在一个预先给定的停息时间Tf内收敛到平衡点的一个预先给定的邻域内,并且该停息时间Tf与系统初始状态无关;2)所有信号是实际有限时间稳定的;3)外部扰动对系统的影响能够被H∞性能抑制.

证明.定理1 的证明过程分为以下3 个部分.

1)跟踪误差e1(t)满足预设性能指标的证明

选择系统总的Lyapunov 函数为

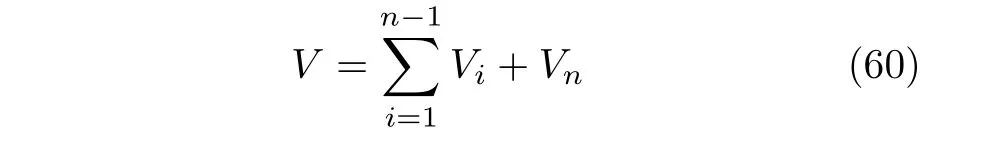
因为V1≥0,V2≥0,···,Vn-1≥0 并且Vn＞0,易知V ＞0恒成立.根据式 (26),式 (29)及式 (53),有

考虑式(61)和式(62)并选择ζ=min{c/2,h},有

应该指出,当|e1(0)|的值较大时,只需要增大设计参数α0而不需要改变αTf,即可满足条件|e1(0)|＜α(0).

2)系统所有信号均为实际有限时间稳定的证明

由于e1(t)能够在有限时间内收敛到给定的界中,易知等所有的系统信号是实际有限时间稳定的.因此,这里详细的证明过程省略.

3)系统(1)满足H∞性能指标的证明

为了验证该系统满足H∞性能指标,定义一个辅助函数如下

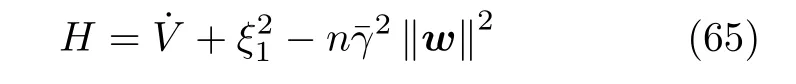
根据式(62)和(65)式,不等式(66)成立.

因为V＞0 且Θ有界,因此必存在一个常数τ使得

对式(67)两边积分,可得

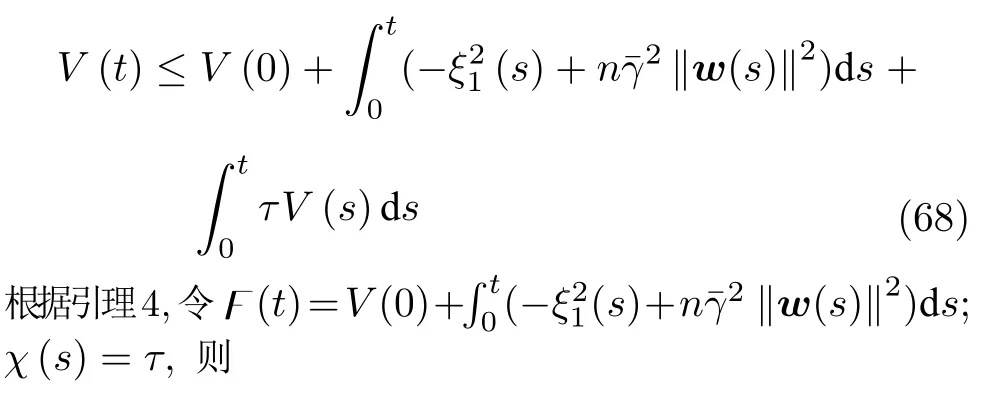
接下来,利用反证法验证 F(t)＞0.假设 F(t)≤0,则V(t)满足

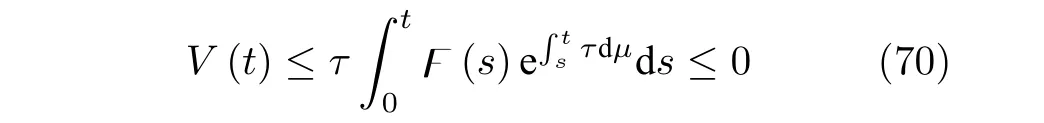
这与V ＞0矛盾.则F＞0成立.即

根据式(71),易有

注3.本文的设计方法能够使得系统在有界稳定的情况下满足H∞性能指标.

3 仿真研究

本节给出两个仿真例子验证所提方法的有效性和优越性.

例1.为了验证本文控制方法的有效性,考虑文献 [27]中的系统.不同的是,在系统中加入了非严格反馈项f1(x)以及外部扰动项w1(t)和w2(t).系统的数学描述如下:

从图1 和图2 可知,即使被控系统初始状态不同并且存在外部扰动,系统的跟踪误差e1(t)仍能被有限时间性能函数α(t)约束,并在给定的停息时间 0.6 s 内收敛到给定的区间 (-0.01,0.01);且系统输出y(t)能够在给定时间内跟踪上信号yd(t),验证了本文控制方法的有效性.

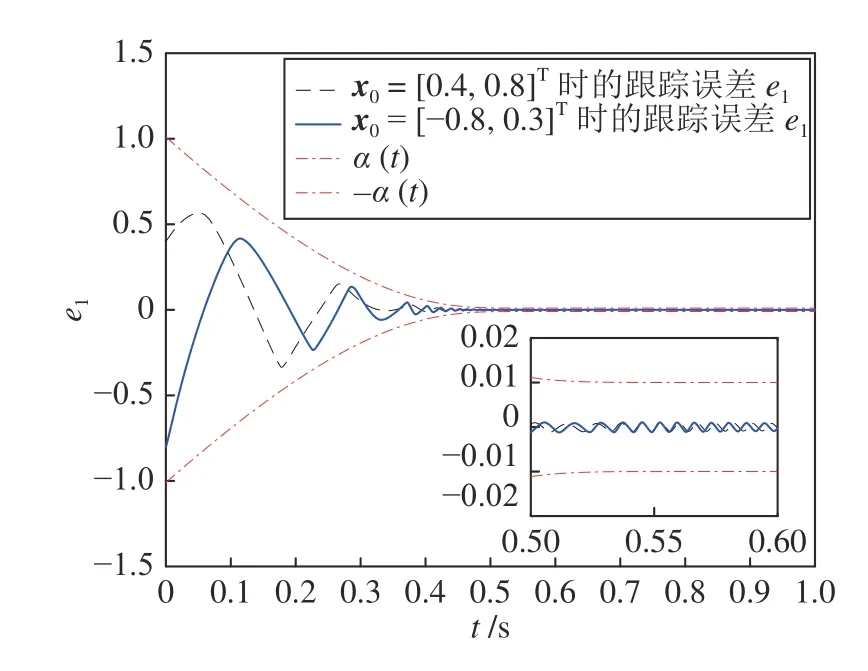
图1 跟踪误差e1Fig.1 Tracking errore1

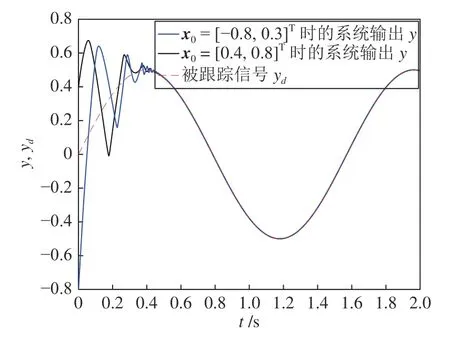
图2 系统输出y跟踪效果Fig.2 Tracking effects of the system outputy

例2.为了验证本文控制方法的实用性和优越性,采用文献 [22]中的机械臂系统.不同的是,一个较大的外部扰动w1(t)被加入到该系统中.这里将本文控制方法与文献 [22]的方法进行对比研究.系统数学描述如下:

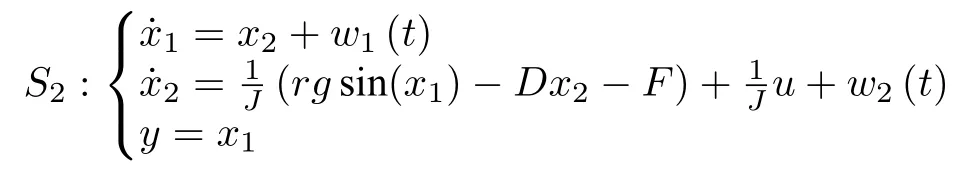
其中,J=3.287,r=2.3126,g=9.8,D=18.6918,F=24.25;w1(t)=5e-0.5tcos(5πt)和w2(t)=0.5e-0.5t×sin(4πt)为系统外部扰动.这些参数的具体物理意义见文献 [28].为了能够与文献 [22]的方法进行比较,这里考虑镇定问题,即e1=x1.选择设计参数k=1;λ1=λ2=1;α0=0.8;αTf=0.03;=1.2;h=1;β1=β2=1;Tf=0.5;自适应参数的初始值=0.5;初始状态选择为x(0)=[0.4,0.8]T;神经网络的选择与系统S1相似.根据定理1 及文献 [22]分别得到两种方法对应的控制器进行仿真.当没有外部扰动时,仿真结果如图3～5所示.图3 给出了两种不同控制方法所得到的状态x1曲线;图4 给出本文控制输入u曲线,图5 为文献 [22]的控制输入u曲线.类似地,当外部扰动存在时,保持两种方法的控制器不变,仿真结果如图6～8 所示.从图3～5 可知,比起文献 [22],本文控制方法收敛速度更快,并且控制器的抖震现象较轻.因此,本文控制方法更实用.根据图6～8 可知,即使系统存在较大的外部扰动,本文方法仍能使被控系统具有较好的动态性能,而文献[22]的控制方法则受到了很大的影响.但是应该说明的是,本文方法使被控系统具有更快收敛速度的同时,会需要较大的控制输入信号.

图3 无外部扰动时状态x1Fig.3 Statex1 without external disturbance

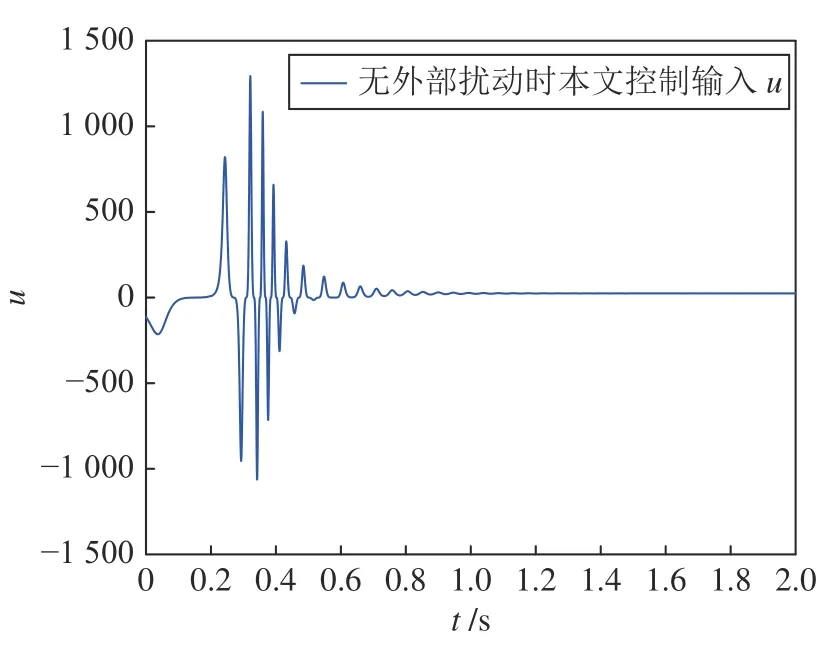
图4 无外部扰动时本文的控制输入uFig.4 Control inputuof this paper without external disturbance

图5 无外部扰动时文献 [22]的控制输入uFig.5 Control inputuof [22] without external disturbance

图6 存在外部扰动时状态x1Fig.6 Statex1 with external disturbance

为了验证本文控制方法在高频变化的扰动下仍能保证较好的控制性能,这里将扰动w1(t)改为信噪比为10.8306 dB的高斯白噪声信号.仍考虑镇定问题.设计参数与初始条件等均不变.对应的仿真结果如图9 和图10.图9 为状态x1曲线;图10 为外部扰动w1(t)曲线.从图9 可知,即使对于高频变化的外部扰动,本文控制方法仍有较好的控制性能.

图7 存在外部扰动时本文的控制输入uFig.7 Control inputuof this paper with external disturbance

图8 存在外部扰动时文献 [22]的控制输入uFig.8 Control inputuof [22] with external disturbance

图9 白噪声扰动下的状态x1Fig.9 Statex1 with white noise disturbance

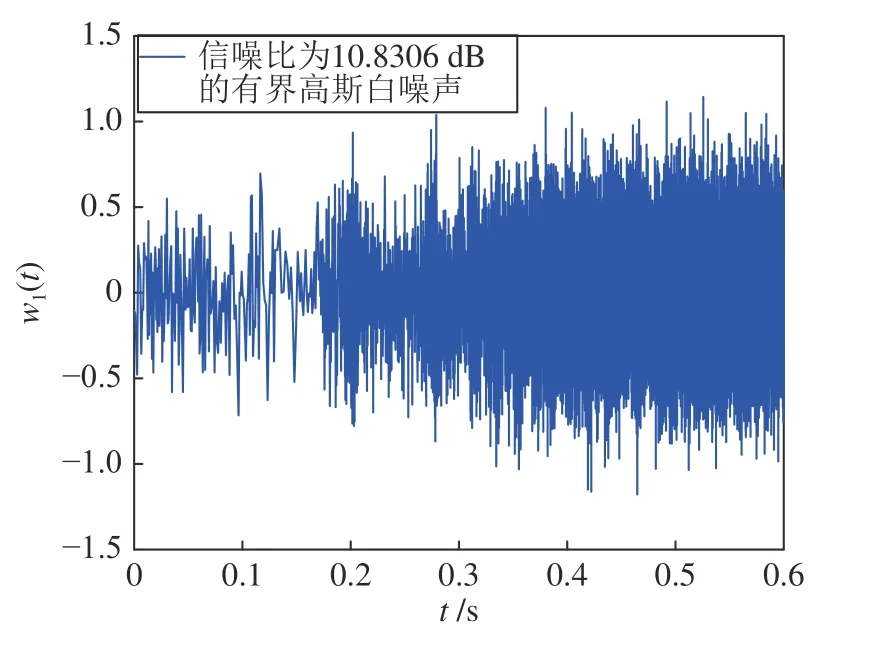
图10 外部扰动w1(t)Fig.10 External disturbancew1(t)

4 结论

本文主要研究了一类带有外部扰动的非严格反馈p规范型非线性系统的预设性能有限时间H∞跟踪控制问题.针对一类p规范型非线性系统提出了一种新的预设性能控制设计方法.并在此方法的基础上,结合加幂积分技术、H∞控制方法以及神经网络自适应技术,设计了自适应神经预设性能有限时间H∞跟踪控制器.该方法避免了预设性能的共性问题.所设计的控制器能够保证系统的跟踪误差被约束在有限时间性能函数 (-α(t),α(t))内.并能够在预先给定的停息时间内收敛到平衡点的一个预先给定的邻域内,且该停息时间与系统初始状态无关.同时,外部扰动对系统的影响能够被抑制.