基于相似度的保障资源相似性识别计算方法研究

辛冀，张乐

（中国直升机设计研究所，江西 景德镇 333001）

0 引言

保障设备是直升机保障系统的重要组成部分，主要负责直升机的使用保障、维修保障和训练保障，保障设备的规模和先进性在保持直升机战斗力方面发挥着重要作用。因此，进一步地提高直升机保障设备的通用化、集成化和先进性，促进保障设备向“横向通用化、纵向系列化”方向发展，使之与多机型联合作战、快速机动部署需求相匹配，更好地服务于作战和核心能力，成为在研直升机研制的重要内容，也是直升机保障能力提升的重点方向。

本文研究和建立异型保障资源相似性计算机规则，进行资源相似性分析，智能地识别不同保障任务具有种类、相似关键特征的保障资源，给出相似资源归并建议。

1 异型保障资源相似性计算规则

针对不同的保障资源，进行相似性计算时，需要考虑资源本身的属性，包括：功能、重量和外观几何因素等，还需考虑相关目标子系统/部件、使用频率等因素。这里我们主要讨论保障资源相似性评价计算的数据稀疏性问题，以及由此引起的扩展性问题。

1.1 保障资源保障特性矩阵的稀疏性

保障资源相似性评价通过收集保障资源的保障特性关联信息来构建保障资源-保障特性关联信息矩阵R（m，n）。其中，R（m，n）使用保障资源的使用时间（或频率）来表示。基于该矩阵计算各个保障资源之间的相似性大小，进而寻找与目标保障资源具有相似特征（功能）的保障资源构成目标保障资源的最近邻集合。由于保障资源相似性的评价基于保障资源关联数据，如果保障资源的关联信息不足，往往会导致保障资源相似性评价的误差与错误。

然而，在航空母舰等一些大型复杂装备系统中，其保障资源及其相应的保障特性的数量都是非常庞大的，但是某个保障资源之间的共同特性却不多，尤其是相对于所有保障资源的总体特性集合来说，往往只是其中的一小部分，这样势必造成保障资源-保障特性矩阵非常稀疏。

这种稀疏性带来的影响有好有坏，好处是这符合实际的情况，对于没有共同特性的资源可以认为不具备相似度；坏处是对于共同特性较少的资源，可能会导致保障资源相似性评价不够准确。

在保障资源-保障特性关联信息矩阵非常稀疏的情况下，基于该矩阵计算得到的保障资源相似性结果往往与实际情况相差甚大。一个稀疏的保障资源-保障特性关联信息矩阵如表1所示。从表1中可以看出，各种保障资源都有保障特性重量，因此保障资源与保障特性矩阵中，重量一列均有数值，但有部分保障特性仅少数资源具有，比如仅蓄压器冲气设备等少数设备具有流量的保障特性，造成矩阵中流量一列仅蓄压器冲气设备一行有具体的数值，其余各行均为空；而输出功率，最大允许误差等保障特性也有类似现象，导致保障资源与保障特性矩阵的稀疏现象。此时若根据传统的相似度计算，由于蓄压器冲气设备和起降甲板电源只有一个共同特性重量，且较为接近，则认为二者具有极高的相似度。然而单凭一个或少数几个保障特性就判断二者有很高的相似性往往是不准确的，甚至是荒谬的。

1.2 保障资源的相似度计算

在已有的方法中，对于要知道个体对象间差异的大小，进而评价个体的相似性和类别。先设定我们要比较保障资源X个体和保障资源Y个体间的差异，它们都包含了N个维的特征，即X=（x1，x2，x3，…xn），Y=（y1，y2，y3，…yn）。主要可以用距离度量和相似度度量两大类方法来衡量两者的差异。在数据分析中有K均值算法等[1]。

1.2.1 距离度量

距离度量（Distance）用于衡量个体在空间上存在的距离，距离越远说明个体间的差异越大。

a）欧几里得距离（Euclidean Distance）

欧氏距离是最常见的距离度量，衡量的是多维空间中各个点之间的绝对距离。公式如下：

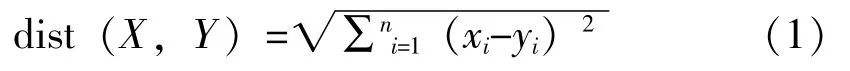
因为计算是基于各个维度特征的绝对数值，所以欧氏度量需要保证各个维度指标在相同的刻度级别，比如对身高（cm）和体重（kg）两个单位不同的指标使用欧式距离可能使结果失效。

b）明可夫斯基距离（Minkowski Distance）

明氏距离是欧氏距离的推广，是对多个距离度量公式的概括性的表述。公式如下：

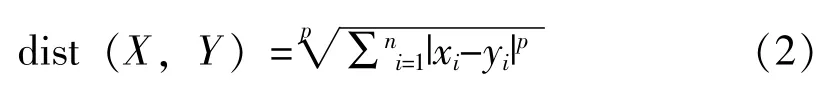
这里的p值是一个变量，当p=2的时候就得到了上面的欧氏距离。

c）曼哈顿距离（Manhattan Distance）

曼哈顿距离来源于城市区块距离，是将多个维度上的距离进行求和后的结果，即当上面的明氏距离中p=1时得到的距离度量公式如下：

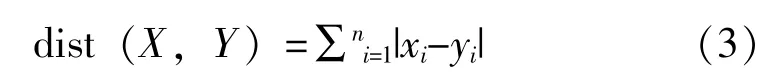
曼哈顿距离和欧氏距离都是明可夫斯基距离在特殊条件下的应用。

1.2.2 相似度度量

相似度度量（Similarity），即计算个体间的相似程度，与距离度量相反，相似度度量的值越小，说明个体间相似度越小，差异越大。

a）向量空间余弦相似度（Cosine Similarity）

余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上。公式如下：

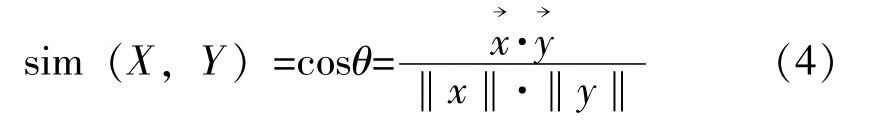
b）皮尔森相关系数（Pearson Correlation Coefficient）

即相关分析中的相关系数r，分别对X和Y基于自身总体标准化后计算空间向量的余弦夹角。公式如下：

c）Jaccard相似系数（Jaccard Coefficient）[2-3]

Jaccard系数主要用于计算符号度量或布尔值度量的个体间的相似度，因为个体的特征属性都是由符号度量或者布尔值标识，因此无法衡量差异具体值的大小，只能获得“是否相同”这个结果，所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。

对于异型装备的通用化设计来说，装备具有的共同特性数量越多，通用化设计的可行性越高。因此Jaccard相似系数是衡量装备相似度特性的核心。

如果比较X与Y的Jaccard相似系数，则只比较xn和yn中相同的个数，公式如下：

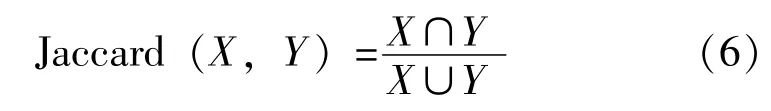
1.3 融合Jaccard与余弦的相似度计算

由于异型装备的通用化设计对于装备特性的数量和具体数值的大小都有比较大的要求，而针对单一的相似度计算无法同时考量共同特性的数量与数值的问题，本报告采取融合Jaccard与余弦的方式进行计算，具体的相似度计算公式如下：

从公式（7）中可以看出，X装备与Y装备的相似度由两个部分决定：1）由Jaccard所代表的共同特性数量衡量；2）由余弦cos所代表的共同特性数值相似度表示。使用融合Jaccard与余弦的方式进行相似度计算，可以同时考虑共同特性的数量和数值，并且进行统一量化；同时，把Jaccard公式看做权重，可以认为是根据共同特性的数量进行相似度衰减，在稀疏数据的情况下，可以取得较为准确的异型装备特性的相似度。

2 基于保障资源功能的相似性计算

参考前面章节介绍的相似度计算的方法，考虑保障资源的相关属性，抽象出保障资源的属性向量，该向量包括保障资源的保障类型、体积、重量和保障频率等信息。每个保障资源作为一个向量P（p1，p2，p3，...pn）。在整个保障任务中，根据保障任务协同仿真中对相关保障资源和工具，进行大的分类，包括：通用保障与不同型号的专业用保障资源。通过计算得出通用资源的相似性矩阵，保障资源的相似性采用常用的余弦相似度的公式。对保障资源相似性矩阵按照评分的多少，进行相似性分析，给出保障资源归并建议。具体的流程如图1所示。

图1 通用保障资源相似性评估

对于保障资源，根据保障资源的保障类型、功能和几何参数等特点，给出保障资源的量化表示。每个保障资源之间采用融合Jaccard与余弦相似度计算的方式，得出保障资源之间的相似程度。结合保障资源之间的特征，给出资源的归并建议。

3 应用实例

针对本专利研究的保障资源相似性识别计算方法，融合Jaccard与余弦的相似度计算方法，首次提出了直升机保障资源相似度识别方法以识别异形保障资源中各个属性的相似度，具体步骤如下所述。

a）装备的选择

本节以直升机的电气系统的相关保障工具为例，分析其相似度。选取较为典型的工具，例如：电源车、万用表、电刷提取器、电机电刷量具和蓄电池充放电站5种工具资源。

b）特性的选择

特性的选择上，关注工具经常使用的几个属性如：重量、体积、功能和使用频率4个因素。

c）向量化表示

分别用T1、T2、T3、T4和T5表示电源车、万用表、电刷提取器、电机电刷量具和蓄电池充放电站5种工具资源，每一个向量由4个维度组成，分别表示重量、输出功率、使用人数和频率（平均每日使用次数）。具体如下：

d）相似度计算

采用融合的Jaccard余弦相似度进行计算，得出5个资源之间的相似度矩阵，如下所示：

从相似度矩阵分析，相似度最高的是T3与T4达到0.998，建议进行通用化归并。值得注意的是，按照普通余弦公式计算，T1和T5的相似度会较高，但经过引入Jaccard进行相似度修正，综合考虑相似保障特性的数量，对相似度进行了惩罚，导致相似度更符合实际，类似的情况还存在于T2和T3、T4之间。

4 结束语

由于保障空间和其他条件的限制，对于直升机装备的保障资源的携带非常受限。开展保障资源通用化研究，减少携带的保障资源种类和数量，对于提升直升机的保障效能具有非常重要的意义。本章节研究和建立异型保障资源相似性计算机规则，进行资源相似性分析，智能地识别不同的保障任务具有种类、相似关键特征的保障资源，并给出相似资源归并建议。

现有的保障设备与工具，主要是根据需要保障的飞机装备不同的子系统，配套提供。存在准备冗余与不足的问题。在进行通用资源优化设计时，对于现有的保障资源与设备的相似性评估分析作为其中最为重要的一步，由分析的结果决定哪些保障资源需要集成，作为通用的保障资源工具。