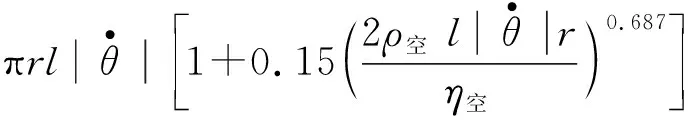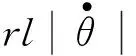单摆周期的系统误差分析
2022-01-13邵云
邵 云
(南京晓庄学院 电子工程学院,江苏 南京 211171)
一般来说,对单摆的周期产生影响的系统误差因素,包括摆角、摆球绕质心轴转动、摆线质量、空气浮力、空气阻力这5种.对于这个古老的问题,目前国内已有的研究文献众多.纵观这些研究文献,可以发现如下问题:1) 考虑得不够周全,漏掉了其中某些因素,尤其是空气阻力;2) 内容缺失,缺少必要的推理和计算过程,缺少必要的背景知识介绍(如大摆角椭圆积分)和图、表等;3) 缺乏必要的近似处理,使结论不够直观;4) 忽视了各种因素误差的符号及彼此间的相互抵消作用;5) 将空气阻力视作速度的一次函数而非实际的二次函数形式,进而缺失了对于空气阻力的正确判断.本文拟将尽量完善对于单摆周期系统误差的讨论,力争弥补以上缺陷,努力为读者呈现一个较为完整和正确的认识.
1 小幅、大幅单摆周期的理论值
设图1中单摆小球的质量为m,其质心到悬挂点O的距离为l(摆长).当摆线偏离竖直方向θ角时,由力学知识可知,作用在小球上的重力G的切向分力大小为mgsinθ,方向趋向小球的平衡位置O′,此时小球运动的动力学方程为
(1)

图1 单摆
当θ<5°时,有sinθ≈θ,式(1)简化为
(2)
这是一个典型的简谐振动微分方程,其通解为
θ(t)=θmaxcos(ω0t+φ)
(3)
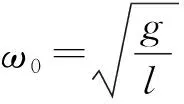
(4)
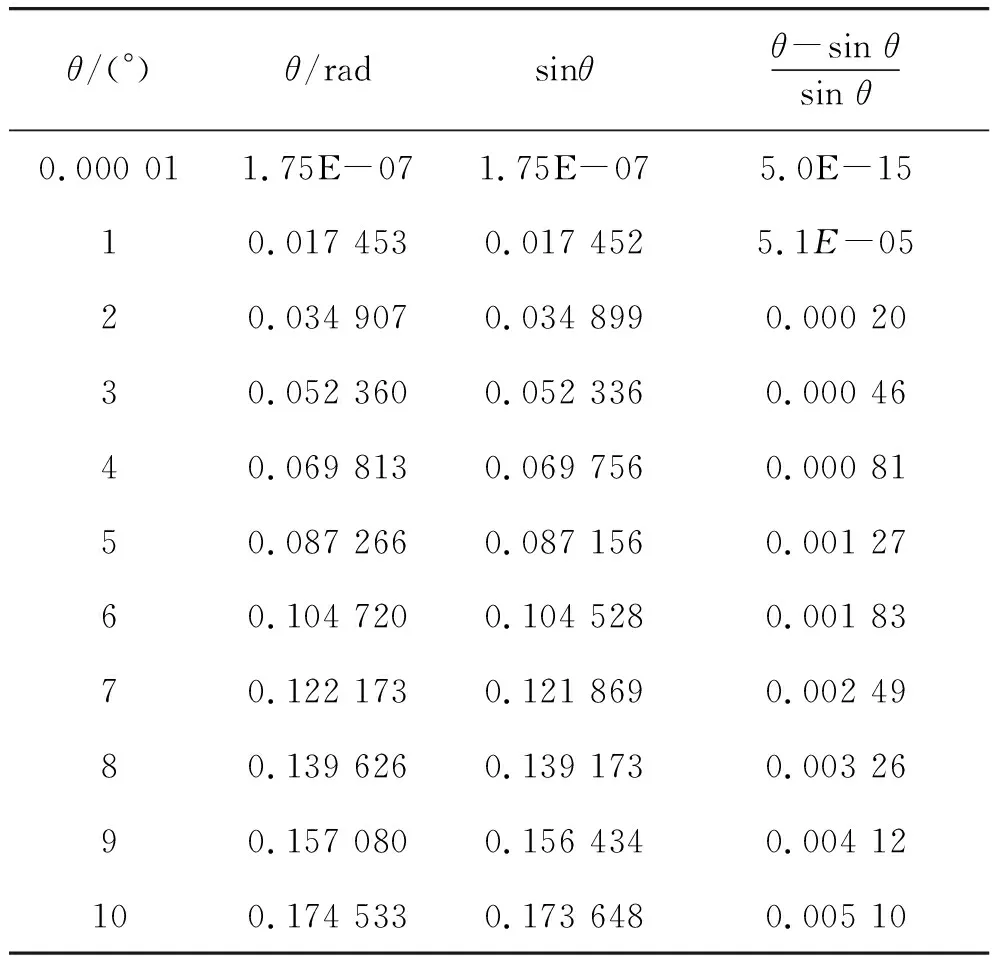
表1 小角度下θ与sin θ的差距
见表1,当θ>5°时,通常认为sinθ≈θ不再成立,此时微分方程式(1)不再是线性方程,其解实际是一包含椭圆积分的隐函数[1,2].对于单摆自右侧最高点静止开始下摆的过程,式(1)的解可以表达为[2]
(5)
其中F是椭圆积分函数,θ0是初始摆角,变量ψ则为
(6)
显然,当单摆下摆至最低点时有θ=0,ψ=0,于是根据式(5),即得此时单摆的1/4周期为[1]
(7)

表2 不同初始角θ0下的1/4周期和小角度近似值比较
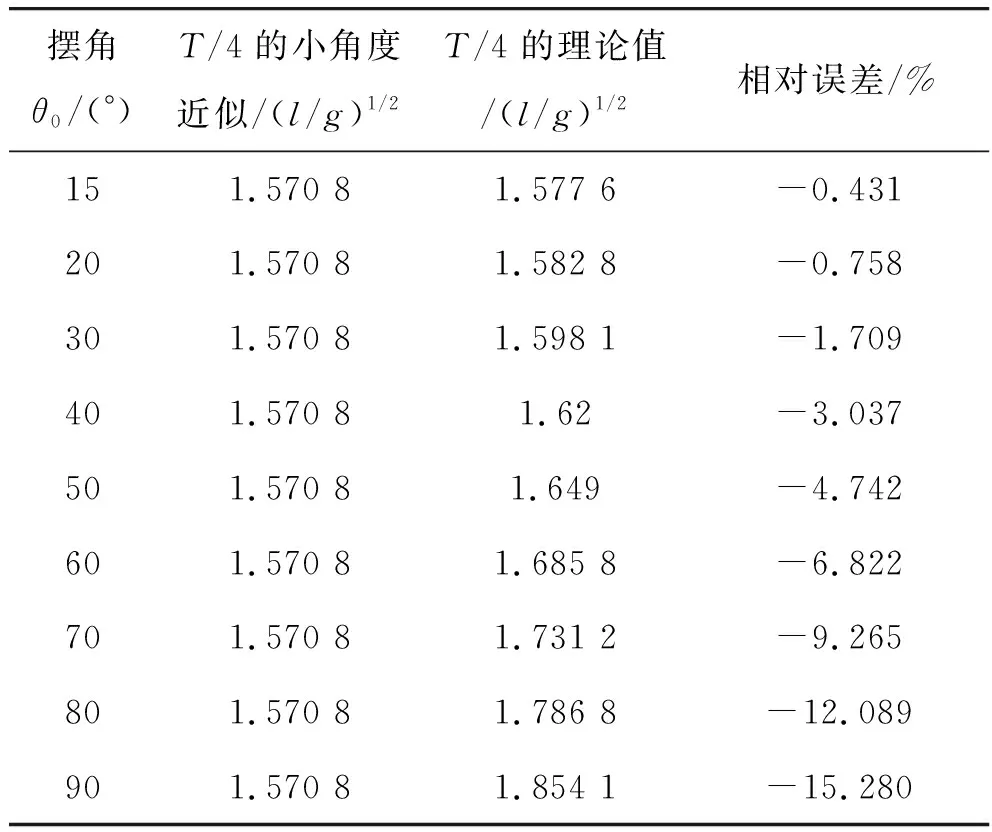
续表
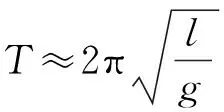
下面将讨论小球绕质心轴的转动、摆线质量、空气浮力及空气阻力对于单摆周期的影响.
2 小球绕质心轴的转动动能对于单摆周期的影响
单摆实验中的小球实际是有大小的,设其半径为r.可将小球和摆线即单摆系统看作刚体,则由刚体力学知识知,系统绕悬点O轴的转动惯量为
(8)
其中已忽略摆线的质量.于是,根据系统绕悬点O轴转动的角动量定理(即转动定理)可得
(9)
整理得
(10)
对比式(10)与式(1)即可发现,在考虑小球的半径r后,单摆的运动形式并没有变化,只是周期稍稍增大.再结合式(4)、(7)可知,无论摆长、摆角大小,在相同的摆长l及摆角θ0下,考虑与未考虑小球半径,周期的相对变化均可表达为
(11)
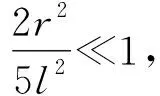
(12)
若取通常值r=0.01 m,l=1 m,则有
(13)
即使取r=0.01 m,l=0.2 m,依然有
(14)
可见,即使计入小球的自转因素,由于转动动能远远小于平动动能[参考式(8)],因此小球自转所带来的对于周期的增加修正也微乎其微,完全可以忽略不计.
当然,摆长中必须计入小球的半径,这一点至关重要.
3 摆线质量对于单摆周期的影响
设摆线的质量为m′,那么系统绕悬点O轴的转动惯量变为
(15)
其中已将摆线长度设为摆长(下同),由此带来的相应误差属于高阶小量,均可忽略.于是,根据系统绕悬点O轴转动的角动量定理又可得
(16)
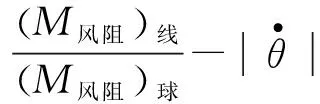
由于m′< (17) 设摆线的线密度λ=0.2 g/m[3],长度l=1 m;小球的密度取ρ=8.9 g/cm3(纯铜摆球),半径r=1 cm,则式(17)中的 (18) 将这里的结果与式(13)、(14)进行对比,可以发现,摆线质量对于周期的影响将随摆长而增加,而小球的自转对于周期的影响则随摆长的增加而迅速减小.此外,式(17)业已表明,这两种因素的影响均与摆角幅度θ0无关. 设空气的密度ρ空=1.29 kg/m3(标准状态),由于摆线通常较细,其体积远小于小球的体积,因此作为近似处理,可将式(16)、(17)中的重力加速度g置换成“视重力加速度”,有 (19) 于是,当继续考虑空气的浮力后,单摆系统的动力学方程需改为 (20) 再将式(19)代入式(20),根据近似知识即可得 (21) 一个有趣的现象便是,从式(21)可见,小球自转、摆线质量、空气浮力这3种因素对于单摆周期的影响存在相消行为.以摆长l=1 m为例,从上文中的数据即可算出这3种因素最终对于周期T的影响合为 (22) 可见,这3种因素总体会导致单摆的周期T减小,其中摆线的质量是主导因素. 其实无论小球还是摆线,空气对它们都会有阻力作用.此时摆线可视作圆柱体,图2为圆柱体做侧向垂直平动时空气阻力系数CD柱与雷诺数Re的关系[4-6];而速度不大的小球的空气阻力系数则为[7] (23) 图2 圆柱体侧向平动的空气阻力系数与雷诺数的关系 静止的空气中雷诺数的定义为 (24) 其中v为物体相应的特征速度;L为物体的特征长度,对于这里侧向平动的圆柱,L即为圆柱的直径,而对于摆球,L则为摆球直径;η空是空气的黏滞系数,在0 ℃时有[8] η空=1.7×10-5Pa·s (25) 对于通常摆长1 m的单摆,其周期为2 s,5°摆角小球的振幅约为0.09 m,因此小球在最低点的速度约为0.09π≈0.28(m/s).现设小球的半径依然为1 cm,摆线阻力的有效直径d有效=0.5 mm,将诸数据代入式(24),即得小球及摆线下端的最大雷诺数分别为: (26) (27) 由此可见,对于这里的小球,将空气阻力系数表达成式(23)是适当的,而图2中雷诺数的范围则显得过于宽泛,只需取其中(0.1,50)区间段即可.为了获得更好的相关系数R2,使其尽量趋于1,本文选择了图2也即文献[4]中插图7.7的Re∈(0.2,10)段曲线进行分立取点,作图并加以拟合,得到图3,所得拟合函数为 CD柱=10.705Re-0.622, 0.2≤Re≤10 (28) 除了极小和极大的速度外,运动物体在空气中受到的空气阻力一般表示为 (29) 其中S是物体在迎风面的最大投影面积.联立式(23)、(24)、(28)、(29),结合其它相关知识,积分便得小幅度单摆受到的空气阻力大小为 (30) 计算整理得 (31) 再将l=1 m,r=1 cm,d有效=0.5 mm及相关数据代入式(31),即得 (32) 另外,参照式(30)—(32),亦可求得此单摆受到的空气阻力矩大小为 (33) 式(32)、(33)均采用了国际单位制. 参见图1,设单摆的初始摆角θ0=-5°.综合考虑本文所讨论的各种因素,并参照上文已有的结论,包括式(16)、(19),对于单摆向右摆的过程,根据角动量定理有 (34) 将l=1 m,r=1 cm,m=3.728×10-2kg以及式(18)、(19)、(33)代入式(34),于是可得 整理得 (35) 考虑到单摆做往复摆动,式(35)应进一步修订为 (36) 这便是小幅单摆在上述5种因素共同作用下的动力学微分方程.据此,应用MATLAB软件,可作出小幅单摆在理论上的摆动图像,如图4所示. 图4 5种因素共同作用下5°单摆摆动的理论图像 由图4可见,即使是小幅度单摆,它在空气中摆动时摆幅的衰减也是较为明显的.经过仔细的考察可知,前100 s摆幅的衰减率约为-0.585°/102s,与文献[6]中秒摆-0.62°/102s的实测结果基本相仿,差异可能源自摆球材质、摆线粗细、空气密度等不同.此外,图4中单摆摆动的周期几乎不变:在0~100 s内的平均周期约为2.007 s,而在900~1 000 s内,平均周期则约为2.006 s. 从表2中可见,1 m长5°摆角单摆的理想周期为 (37) (因g相同及比较需要,结果多取了几位有效数字)因此,图4中多种因素共同作用下的小幅单摆周期的相对误差(取前100 s)为 (38) (39) 单摆实验的确是一个系统误差极小的实验,因此它能够被用来测量重力加速度g.此时若以1‰的测量精度为目标,那么摆角θ0只能选择5°左右,而摆长l则须选择1 m及以上. 需要指出的是,不少研究单摆的文献[3,9,10]都将空气阻力表达成斯托克斯一次正比黏滞阻力,这是不恰当的,因为该公式只能适用于雷诺数Re比1小很多时的情形[4,5,8],如空气中十分微小的水滴或油滴等.事实上,从本文式(31)也能明确地看出这一点.在式(31)中,小球受到的空气阻力显然为 (40) 看起来,它和小球的斯托克斯一次正比黏滞阻力 (41) 颇为相似(确实存在联系[4,5]),但是实际数值却差别很大.根据式(40)、(41)并利用式(32)中的数值可得 (42) 图5 本文5°单摆下摆时小球所受风阻比(F风阻)球/F斯随角速度|dθ/dt|的变化 另外,从式(33)亦可看出,摆线与摆球受到的空气阻力矩之比为 (43) 图6 5°单摆的摆线与小球受到的空气阻力矩之比随角速度的变化4 空气的浮力对于单摆周期的影响
5 小幅度单摆受到的空气阻力及其力矩

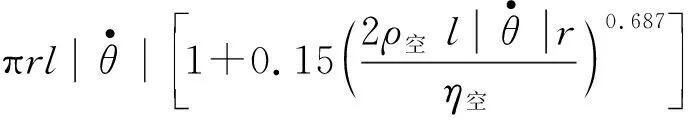
6 小幅单摆较严格的理论周期及空气阻力影响
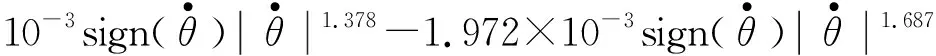
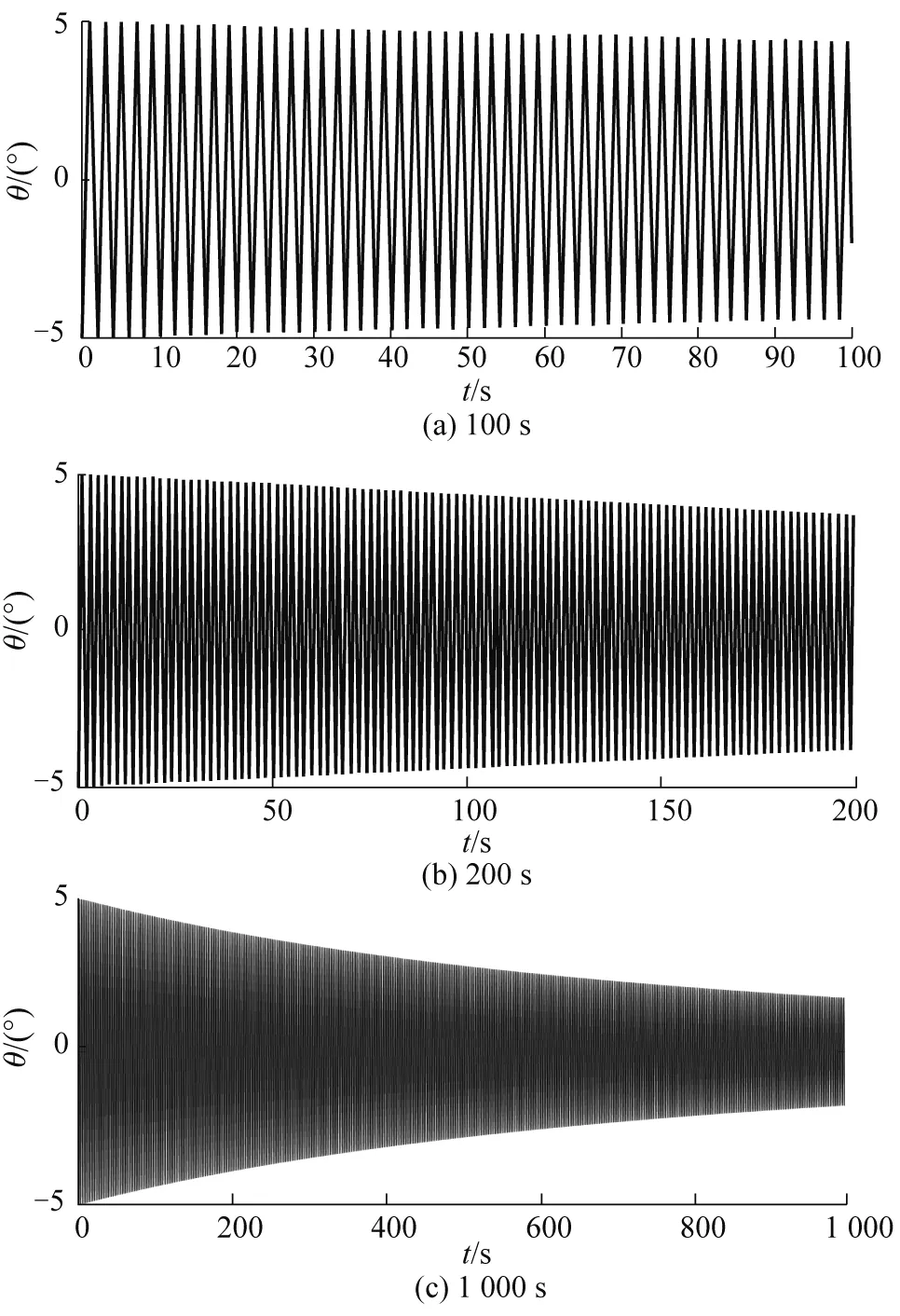

7 单摆周期系统误差的综合分析
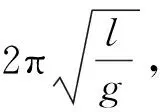
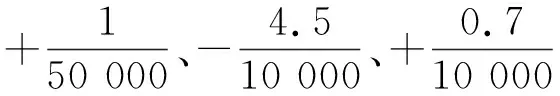
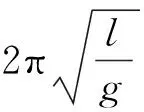
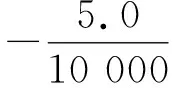
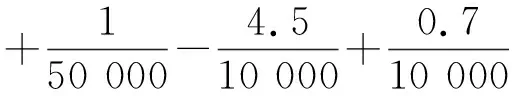
8 关于空气阻力的几点补充说明