电动汽车混入条件下多方式动态交通分配模型

张 锐，姚恩建，张永生

（1. 长安大学 运输工程学院，西安 710064，中国；2. 北京交通大学 交通运输学院，北京 100044，中国）

研究电动汽车混入条件下多方式动态交通分配模型，对于合理规划充电设施，推动电动汽车的普及应用具有重要意义。其中，交通分配模型性能的优劣取决于路径选择模型背后行为假设的合理[1]。电动汽车驾驶员在出行过程中常伴随充电需求判别、充电设施选择等行为。J. G. Smart和S. Schey[2]研究了美国部分地区纯电动汽车用户的充电行为，发现18%的充电行为发生在出行途中。YANG Yang 等[3]提出用来解释电动汽车用户行为选择机理的嵌套Logit（nested logit,NL）模型，并指出起点和终点处的电池荷电状态（state of charge, SOC）是影响用户充电决策与路径选择的关键变量。XU Min等[4]基于混合Logit模型，指出在家使用慢充方式的纯电动汽车用户，其充电行为更具有频繁性；在公共充电站使用快充方式的用户，其充电行为更具有必要性。李宗华等[5]基于大数据平台，分析了电动汽车用户的充电及驾驶行为，指出高里程焦虑用户表现出充电次数多、用电谨慎以及极限充电的特征。

大量研究将电动汽车交通流纳入交通分配模型中来研究交通流量的时空分布规律。HE Fang 等[6]基于一系列均衡模型研究电动汽车续驶里程及充电需求对出行者路径选择的影响，以及相应的网络均衡流量分布模式。JIANG Nan 等[7-8]研究了包含燃油汽车与电动汽车在内的混合交通流的需求分布及相应的出行选择。杨扬等[9]考虑出行能耗、旅行时间及充电服务时间等因素，构建了电动汽车混入下的随机用户均衡（stochastic user equilibrium，SUE）分配模型。WANG Hua等[10]考虑在途充电的影响，提出了描述电动汽车用户出发时间和出行路径联合选择的用户均衡模型。XI Haoning等[11]考虑电动汽车用户与燃油汽车用户路径选择标准的差异，构建了环境导向的混合行为用户均衡模型。以上研究针对电动汽车混入下的静态交通分配模型展开，无法反映时变交通需求下的路段状态及其演变过程。郇宁等[12]考虑电动汽车用户的在途充电行为及充电排队行为，提出电动汽车混入条件下的动态用户均衡分配模型，并在此基础上，探究关键因素对充电设施服务水平的影响。ZHOU Zhe等[13]针对交通与电力耦合系统，构建了电动汽车动态交通分配模型以分析交通需求及电力需求的实时分布。然而，以上研究均未考虑电动汽车用户的慢充行为，且行为假设也缺乏实际数据的验证。

与传统燃油汽车相比，电动汽车用户在出行行为方面表现出不同于传统燃油汽车用户的特点。首先，有限的续驶里程是造成电动汽车用户“里程焦虑”的主要原因。受此影响，出行者在出行前可能放弃使用电动汽车，或在使用中产生充电行为，从而产生不同于传统燃油汽车的路径选择结果，直接影响交通分配。其次，除时间、费用等影响燃油汽车用户出行行为的因素外，电动汽车的SOC及能耗等车辆特征也是影响电动汽车用户充电决策和出行选择的重要因素。最后，对有充电需求的电动汽车用户，电动汽车充电设施布局等环境因素对其出行选择行为会造成一定影响。其可选路径须保证其能在电池安全阈值范围内顺利抵达充电站。

基于计量经济学理论的出行行为分析可识别并量化影响出行者出行选择的关键因素，对保障交通分配模型背后行为假设的合理性具有重要意义。本文在深入剖析电动汽车混入下多群体出行者的出行选择行为机理的基础上，构建能够适应电动汽车混入的多方式动态交通分配模型，为电动汽车家用充电设施的配比、充电服务费指导价格的制定及公共充电设施容量配置等实际问题提供决策支撑。

1 多方式交通网络表示

本文重点考虑以地铁和公交车为代表的公共交通出行和以电动汽车和燃油汽车为代表的私人交通出行。基于图论构建多方式交通网络，以此为载体开展出行选择行为分析以及动态交通分配模型构建。

定义：交通网络Y（N,A,M），N为节点集合，A为路段集，M为出行方式集合（当出行方式元素m= U、B、G、E时，分别表示：地铁、公交车、燃油汽车、电动汽车）。R和S分别为起终点集合。r为起始节点，r∈R，s为终止节点，s∈S。J（j= 1：电动汽车在途充电，j= 2：电动汽车终点充电）为电动汽车出行方式的集合。

有限的电动汽车充电站分布在道路交通网络上的某些节点，沿途的电动汽车充电站采用快充模式，终点的电动汽车充电站采用慢充模式。出行方式m下，起终点（origin destination, OD）对rs之间所有的路径集合记为Km,rs，路径km∈Km,rs上所有的路段集合记为Am,rs。对于电动汽车方式，从起点r∈R到充电站nc∈N的路径上所有的路段集合记为A′E,rs。

对有充电需求的电动汽车，以虚拟节点表示电动汽车充电站，以虚拟路段为载体模拟高峰时段有充电需求的电动汽车排队情况。在出行选择行为分析中，基于非集计模型辨识和量化影响出行者方式和路径选择的影响因素，为出行者出行广义费用函数的确定提供支撑，也为随后的动态交通分配模型研究提供基础。其中，交通网络存在n类出行者（n= 1、2、3、4时，分别表示：无车人群、燃油汽车保有人群、电动汽车保有人群、燃油汽车和电动汽车共同保有人群）。

不考虑对于燃油汽车和电动汽车的具体使用频率，这两种交通工具均可作为第4类出行者出行的备选方式。在动态交通分配模型构建中，以出行选择行为结果作为出行者出行选择的依据，基于随机平衡理论和变分不等式方法，提出相应的动态交通分配模型和算法，并通过算例验证模型和算法的有效性。将动态交通分配的研究时段[0,T]划分为I个时段，每个时段记为i（1≤i≤I），长度为Δt；Δt=T/I。

2 出行选择行为分析

基于随机效用理论，用多项Logit（multinomial logit, MNL）模型的表达。若令Vmn为出行群体n选择出行方式m效用中的固定项，则出行群体n选择出行方式m的概率为

针对不同出行群体，构建模型结构如图1所示。

图1 中，对于电动汽车保有者，由于在途充电和终点充电2个选项之间存在隐含关联和共有属性，本文应用NL模型结构建模，可解决MNL模型中 IIA（independent and irrelevant alternatives）特性带来的估算偏离问题，进而通过选项的分层和效用值来描述具体的选择决策行为。

在NL模型中，出行群体n选择交通方式m并同时选择交通方式m中模式j的组合概率为：

式中：V（j|m）n为出行者n选择方案jm时效用中的固定项；Vmn为出行者n选择方案m时效用中的固定项；λ2为NL模型待定层间比例参数；Vmn*为出行者n选择出行方式m时，方案jm对效用产生的复合影响，即：

3 动态交通分配模型构建与求解

3.1 广义出行成本

若假设路段a末端有一个瓶颈，其最大流出率为Sa，则i时刻通过路段a的出行时间为：

式中：Ta,0为路段a的自由流时间，min；qa(i)为i时刻进入路段a的排队规模，辆；γam,km,rs(i)为i时刻OD对rs间进入出行方式m下路径km中路段am的驶入率，辆/min；ρ为公交车折算系数。

为考虑交通流量对车辆能耗的影响，参照文献[14]-[15]，i时刻电动汽车方式下路段a的能耗(ea,E/kWh)为：

燃油汽车方式下路段a的油耗(ea,G/ kg)为

式（8）、（9）中：la为路段a的长度，km。

式（8） -（9）采用路段层面的平均集计参数，在目前的智能交通信息采集系统中更易获取，因而应用范围更广，可支撑后续车辆路径能耗的计算及到达充电站时剩余电量的估算。

公交车、燃油汽车及电动汽车i时刻下OD对rs间路径km的出行时间为：

对电动汽车在途充电模式，当电动汽车的充电时间为变量时，不能保证虚拟路段的出行时间符合先进先出规则。考虑出行者不会在车辆剩余电量较多时采取在途充电模式，且并非所有出行者在途充电都会将电池充满，因此将充电时间统一取为剩余电量较低时固定的车辆充电时间，记为Tck,rs。

对燃油汽车和电动汽车，i时刻下OD对rs间路径km的出行能耗ekm,rs(i)为：

基于文献[16]，i时刻下OD对rs间电动汽车到达充电站时的剩余电量S'(i)为：

最终，i时刻下OD对rs间不同人群不同出行方式下的广义出行成本可描述如下：

式中：hkm,rs,n(i)为i时刻下OD对rs间出行群体n选择出行方式m的广义出行成本；hkj|E,rs,n(i)为i时刻下OD对rs间出行群体n选择电动汽车充电模式j的广义出行成本；TkU,rs为OD对rs间选择地铁线路kU的出行时间，min；hkU,rs为OD对rs间地铁线路kU的固定票价，元；hkB,rs为OD对rs间公交车线路kB的固定票价，元；S'j|E(i)为i时刻下OD对rs间电动汽车充电模式j抵达充电站时的剩余电量；β1为电价，元；β2为汽油价格，元；p0为停车费，元；θi,n为待定系数，i= 1,2,…9。

3.2 交通分配模型

3.2.1 约束条件

路段状态方程可描述为：

式中：xam,km,rs(i)为i时刻OD对rs间进入出行方式m下路径km中路段am的车辆数；xa(i)为i时刻OD对rs间进入路段a的车辆数；gkm,rs(i)为i时刻OD对rs间进入出行方式m下路径km的驶入率，辆/min；vam,km,rs(i)为i时刻OD对rs间离开出行方式m下路径km中路段am的驶出率，辆/min；bm为路段am的紧前路段。

根据先进先出规则及确定性排队理论，i+Ta(i)时刻下路段a的流出率为

i时刻下OD对rs间进入路段a的驶入率为

式中：ζam,km,rs为路径-路段关联参数，当路段am是路 径km的 起 始 路 段 时，ζam,km,rs= 1否 则ζam,km,rs= 0；ζbm,am,km,rs为路段-路段关联参数，在路径km中，当路段bm是路段am的紧前路段时，ζbm,am,km,rs= 1否则ζbm,am,km,rs= 0。

以外，还要满足非负约束、流量守恒约束和边界条件约束：

3.2.2 平衡条件

采用SUE模型来描述出行者的出行决策过程。对无车人群和燃油汽车保有人群，出行者感知的i时刻OD对rs间出行方式m下路径km的广义出行成本函数为：

式中：ξkm,rs,n(i)为出行群体n所感知的OD对rs间出行方式m下路径km广义路径成本的误差项。

则动态交通网络中进入OD对rs间出行方式m下路径km的概率为：

对出行群体n而言，OD对rs间的期望最小出行预算为：

对电动汽车保有人群及燃油汽车和电动汽车共同保有人群，出行者感知的i时刻OD对rs间出行方式m下路径km的广义出行成本函数为：

出行者感知的i时刻OD对rs间出行方式m下出行模式j的广义出行成本函数为：

式中：ξkj|m,rs,n(i)为出行群体n所感知的OD对rs间出行方式m下出行模式j广义成本的误差项。

则动态交通网络中进入OD对rs间出行方式m并同时选择出行方式m出行模式j中路径 的组合概率为

其中，动态交通网络中进入OD对rs间出行方式m出行模式j中路径k的概率为：

动态交通网络中进入OD对rs间出行方式m的概率为：

因此，电动汽车混入下多方式动态交通网络SUE条件可描述为：在均衡状态的动态交通网络中，没有出行者能单方面改变出行路径来减少其期望的最小出行费用，其数学化表达式如下：

式中：gkjm,rs,n(i)为出行群体n中，i时刻OD对rs间进入出行方式m下出行模式j中路径k的驶入率，辆/min。

3.2.3 变分不等式模型

构造与SUE条件等价的变分不等式模型如下：

该模型与电动汽车混入下多方式动态交通网络SUE条件间的等价性可通过式（57）的Karush-Kuhn-Tucker条件推导得出。由于路段出行时间在时间上连续，且连续依赖于路径流入率，同时在i时刻下路径出行成本函数在路径流入率上连续，因此式（57）存在解。但对于包含多个路段瓶颈的交通网络，无法从路段出行时间推导出路径出行成本的单调性，即不能保证式（57）存在唯一解。

3.3 求解算法

步骤1：初始化。

1） 设定初始时段的出发量grs,n(0)，时间段长度Δt，收敛参数ψ；

2） 设置一个空路网，输入网络相关参数，并令路径流入率gkm,rs,n(0) = 0；

3） 设置迭代次数τ= 1，初始时间段i= 1。

步骤2：随机动态网络加载。

1）构造电动汽车两种充电模式下的可用路径集合。其中，电动汽车在途充电模式下的可用路径为经过至少一个在途充电站的路径；电动汽车终点充电模式下的可用路径为与燃油汽车可用路径相同的路径；

2） 计算δaki,rs(l)τ；

3） 根据式（34） - （36）计算路段流入率γa(l)τ；

4） 根据式（7）计算路段排队qa(l)τ，根据式（6）计算路段出行时间Ta(l)τ，根据式（8）和（9）计算电动汽车和燃油汽车的路段能耗ea,E(l)τ和ea,G(l)τ；

5） 根据式（10）计算路径出行时间Tk,rs(i)τ，根据式（11）和（12）计算电动汽车和燃油汽车的路径能耗ekE,rs(i)τ和ekG,rs(i)τ；根据式（13）计算电动汽车到达充电站时的剩余电量S'(i)；

6） 根据式（14） - （29）计算不同人群不同出行方式下的路径成本hkm,rs,n(i)τ；

7） 根据式（43）和（52），（47） - （50）和（53）计算进入出行方式m下路径km的驶入率fkm,rs,n(i)；

8） 更新路径驶入率：9） 判断：若i＜I，则i=i+ 1，转到步骤2.1。

步骤3：收敛检验。当优化函数F满足下式时，算法停止，否则令τ=τ+ 1，返回步骤2。其中，ψ为优化函数F的收敛标准。

4 数值分析

4.1 算例网络

如图2所示，算例网络由15个节点和20个路段构成，含4个虚拟节点和4个虚拟路段。其中节点 3'、节点 4'、节点 10'代表出行途中的电动汽车公共充电站，节点 11'代表出行终点处的电动汽车公共充电站。O1-O3分别对应3个起始点，D对应终点。

路段编号对应的路段通行能力和路段自由流时间信息如表1所示。 其中，路段17-19的自由流时间为电动汽车在途充电时间；路段20的自由流时间为电动汽车在终点处的充电时间，出行过程中不考虑终点处的充电时间。路段17-20的路段通行能力为电动汽车充电站的服务能力，即单位小时可服务的车辆数。

表1 路段信息情况表

关于道路交通网络路径组成，燃油汽车路径为全路网可用路径，电动汽车充电路径为经过充电站的路径，公交车路径如表2所示。

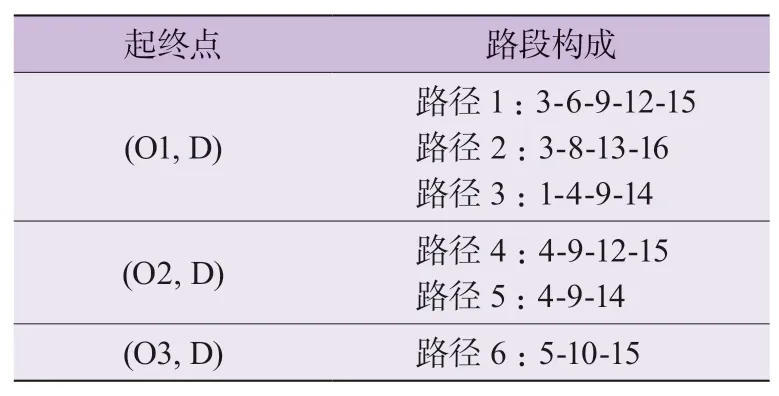
表2 公交车路径组成情况

取研究时段为00:00—24:00，Δt= 1 min，共计1 440个时间片段。目前电动汽车的混入率较低，为探究电动汽车混入对城市交通系统的影响，假设在图2所示的交通网络中，存在3组OD对，每组OD间的4类出行人群，分别占出行需求的50%、30%、10%、10%。对于其他影响因素，均参照现实情况进行设置。电价β1取1.488元/ kWh（含充电服务费1元/kWh及电价0.488元/ kWh），汽油价格β2取9.076元/kg，电动汽车电池的额定容量Q取25.6 Ah，额定电压U取320 V，电动汽车初始SOC取70%。3组OD对下，地铁的出行时间分别为10、8、6 min，对应费用为4、3、3元；公交车的费用统一为2元。地铁和公交车步行时间10 min，等待时间15 min。公交车折算为标准车系数为3，公交车平均载客量为45人/车，私家车平均载客量为1人/车，停车费p0=10元，ψ= 10-4。出行需求曲线在文献[17]的基础上，基于北京市居民出行数据，拟合如图3所示。通过改变常数项z可调整整个出行时段的出行需求总量，本文取3组OD对的z分别为3、2和1。

4.2 出行选择行为模型标定

考虑到目前电动汽车的市场占有率相对较低，采用意向调查（stated preference, SP）获取出行者的出行偏好数据。调查内容主要包括：

1） 出行者个人属性信息：性别、年龄、职业、月收入、小汽车保有情况、电动汽车保有情况；

2） 出行方式选择意向：不同出行场景下出行者的出行方式选择意向。

在意向调查中，设计了多种出行场景。主要考虑2种出行目的（通勤和非通勤）、3种出行距离（短距离、中距离和长距离）以及3种电动汽车初始电量（低电量、中电量和高电量）进行组合场景设计。每一出行场景均根据实际情况计算不同出行方式所需的旅行时间和旅行费用，对于电动汽车，额外估算途中充电站和终点充电站的剩余电量信息。被调查者根据所提供的出行方式选项，选取且只选取一种交通方式出行。调查时间为2017年4月，调查方式为网络调查，主要面向23～60岁年龄段人群，对其出行方式选择相关信息进行问卷调查，经数据筛选处理最终得到有效数据1 143条。运用极大似然法求解上述模型，参数标定结果如表3所示。

表3 出行方式选择模型参数标定结果

结果显示：2个NL模型的层间比例参数分别为0.271和0.503，说明了出行方式选择层与电动汽车充电模式选择层间存在阶层关系，表明所构建NL 模型结构正确[18]。4个模型的调整优度比分别为0.439、0.245、0.218和0.159，说明这些模型具有较好的拟合效果[19]。同时基本所有变量满足5%的显著性标准，有较好的统计有效性。

在各模型中，时间、费用的符号均为负，说明随时间、费用的增加，出行者选择该交通方式的概率降低。电动汽车消耗电量的符号为负，说明电动汽车的选择概率随其消耗电量的增加而降低；电动汽车剩余电量符号为正，说明出行者在出行过程中倾向于选择到达充电站剩余电量较高的出行方式，均符合实际情况。

上述出行方式选择模型参数标定结果，可捕捉影响出行者出行方式和路径选择的关键因素并量化其影响，揭示电动汽车混入下多群体出行者的出行选择行为机理，为后续多方式动态交通分配模型研究奠定出行路径选择行为建模的基础。

4.3 分配结果

基于上述参数设置，执行电动汽车混入下多方式动态交通分配模型求解算法。图4为研究时段内各出行方式流入率的情况。在不同时刻，地铁流入率总大于公交车流入率，其次为燃油汽车流入率，最后为电动汽车流入率。这种现象说明出行者对于低成本或便捷出行方式的喜好，同时也反映出电动汽车目前在市场普及方面仍面临一定的挑战。

在算例网路中，终点充电站11处存在排队，具体排队形成及消散情况如图5所示。

假设电动汽车驾驶员在途充电使用快充模式，平均停留时间15 min，在终点处采用慢充模式，平均停留时间6 h。在电动汽车充电站编号3、4、10、11处，分别有充电桩10、13、4、160个，因此4个充电站每小时的服务能力分别为40、52、16、10辆。相比之下，电动汽车充电站处的通行能力远低于其他路段，因此在路网中产生了排队现象。另外，由于终点充电的出行成本较低，选择人数多于在途充电人数，因此终点充电站最早形成排队并且消散也较慢，在现有路网条件与政策条件下，终点充电站无法在晚高峰到来之前清空原有的排队。值得注意的是，终点充电站处的平均排队长度最高为17辆，平均排队时间1.92 h，服务水平较低。

4.4 灵敏度分析

考虑电动汽车家用充电设施的保有情况及公共充电设施的服务水平，探讨电动汽车初始SOC、充电服务费及充电桩数量3个因素对交通系统的影响。电动汽车初始SOC在一定程度上反映了家用电动汽车充电设施的配比情况。图6为电动汽车初始SOC与全天累计电动汽车流入量的动态关系。

图7 为不同充电服务费下的系统成本变化情况。

在算例中，假设当电动汽车到达任意充电站的剩余电量小于20%的电量时，该出行方案不可用。因此，当电动汽车初始SOC在20%以下时，全路网的电动汽车累计使用量为0，而随着初始SOC的不断增加，电动汽车累计使用量先是急剧上升，随后平缓增加，说明家用电动汽车充电设施保有情况的改善可在一定程度上促进电动汽车的使用。

在中国，电动汽车充电成本主要由电费和充电服务费2部分构成。对充电设施运营商，除运营初期政府给予的充电桩建造成本补贴外，充电服务费是目前最主要的盈利渠道。保持原有网络参数和政策参数不变，调整现有充电服务费价格，分析出行者和电动汽车运营商的成本变化情况，以及路网CO2的排放情况。其中，用户成本为研究时段全路网出行者的总出行成本；由于充电服务费不会对电动汽车充电站运营商的建造成本产生影响，这里考虑电动汽车充电站运营商的运营收益，即充电服务收益与停车收益之和；不同出行方式的CO2排放因子取文献[20]中的建议值。

如图7所示：随着充电服务费的增加，用户成本不断降低、电动汽车充电站运营收益及CO2排放不断增加。这是因为充电服务费的增加，使原先选择电动汽车的用户向其他出行方式转移（大部分向公共交通转移），因此用户总成本降低。而由于电动汽车的CO2排放因子最低，因此全路网的CO2排放增加。电动汽车充电站运营收益的增加表明，充电服务费价格的增加尽管减少了电动汽车的使用量，但对电动汽车充电站运营商是有利的。因此，如果不考虑电动汽车的社会效益，提高充电服务费价格对交通系统和充电站运营商均是可取的，但该举措不利于电动汽车的普及，也造成了交通系统CO2排放的增加，因此管理部门在指导充电服务费价格时，要统筹环境、用户与充电站运营商三方的利益。

交通分配结果表明：在现有路网条件与政策条件下，在途充电站处完全没有排队，在途充电用户可以“随用随充”，而终点充电站处的服务水平相对较低，排队现象较为严重。因此需对在途充电站与终点充电站的容量配置进行探讨，分析不同充电桩规模设置下的成本、收益与路网性能情况，为电动汽车充电运营商提供较为合理的运营方案。

电动汽车充电站容量配置方案如表4所示，其中，以电动汽车充电站的现有规模为基准场景（在途充电站现有规模为y1，终点充电站现有规模为y2），方案1中在途充电站及终点充电站规模均为现有规模的一半。假设在途充电站全部安装40 kW规格的一体式直流充电机，单价5.46万元，终点充电站全部安装7 kW规格的交流充电桩，单价0.46万元，不同方案下的成本、收益及路网性能情况如图8、9所示。

表4 电动汽车充电站容量配置方案

可以看出：方案1虽大幅降低充电桩的购置成本，但充电设施的短缺却增加了用户成本、CO2排放和平均排队时间、减少了充电站运营收益。相比基准场景，方案2与方案3在降低充电桩购置成本方面具有显著效果，但对其他指标的优化作用不大。假设充电桩平均排队时间30 min以内为可接受范围，则可行方案为6-8。在方案6-8中，用户成本、CO2排放和平均排队时间逐渐降低、充电站运营收益逐渐增加。

相比于用户成本和充电站运营收益，充电桩的购置需要相对较大的投入，因此选择充电桩购置成本最低的方案6为最终的推荐方案，相比基准场景，方案6能够使用户成本降低3.61%，CO2排放降低0.76%，平均排队时间降低77.09%，充电桩购置成本降低15.86%，使充电站运营收益增加14.66%。

5 结 论

本文同时考虑电动汽车的在途充电和终点充电需求，基于非集计模型识别并量化影响出行者出行选择的关键因素，保障交通分配模型背后行为假设的合理性。基于出行选择行为分析结果，构建了电动汽车混入下多方式动态交通分配模型，动态考虑路网容量、电池剩余电量和充电站服务水平等因素，并将充电需求、充电排队等内生变量纳入交通分配的框架中，实现相关政策变量对时变充电需求和路网交通流分布模式的影响分析。

本文提出的模型能合理模拟不同出行群体的出行选择行为，通过算例分析，得到以下结论：

1） 电动汽车充电设施服务水平的提高及家用电动汽车充电设施保有情况的改善，可促进电动汽车的使用；

2） 在电动汽车基础设施建设方面，应统筹考虑环境、用户与充电站运营商三方的利益。