基于设计参数灵敏度分析的模型修正方法研究
2022-01-12张开银方来文
张开银 许 灿 张 斌 方来文
(武汉理工大学交通与物流工程学院1) 武汉 430063) (中建三局国际工程公司2) 武汉 430071)
0 引 言
对于桥梁结构而言,一方面桥梁在运营过程中会出现构件的性能退化,截面破坏等因素偏离设计参数(如截面尺寸、密度、弹性模量等);另一方面,在建模过程中难免存在一些理想化或简单化的构件模拟(如对单元的离散程度与边界条件进行简化处理),二者都会导致有限元模型与实际结构的差异.因此,为了使有限元模型与实桥结构的响应一致,对有限元模型进行准确的修正显得尤为重要[1-3].
目前,国内外众多学者对桥梁结构有限元模型修正方法进行过大量的理论分析与试验研究[4-5],并对其研究方法进行系统性分类,根据优化方法的不同,分为子结构模型修正法、代理模型修正法、随机类模型修正法.依据实测信息的来源,分为基于静力的模型修正方法、基于动力的有限元模型修正方法、基于静动力的有限元模型修正方法.按照修正对象不同,分为设计参数型修正方法、矩阵型修正方法与响应面法.其中以灵敏度法为基础的有限元模型修正技术得到了广泛的应用,文献[6]对基于灵敏度的有限元模型修正方法进行了系统、全面的讨论,成功应用到Lynx直升机机身的有限元模型中.文献[7]根据桥梁现场实测的模态数据,运用基于灵敏度的有限元模型修正方法对一悬索桥进行了修正,修正后精度满足要求.文献[8]通过摄动待修正参数模拟试验数据,运用灵敏度分析技术对某抗震桥梁进行了准确的修正.一系列基于灵敏度分析的模型修正法表明其具有重大的理论与工程实践意义,值得推广与进一步研究.
文中提出一种将灵敏度分析与设计参数法相结合的有限元模型修正方法,以悬臂梁结构为例建立有限元模型模拟修正过程.以实测的固有频率为基准,通过比较有限元模型计算的固有频率与实测频率之间的相对误差大小,并对其进行灵敏度分析,找出对结构固有频率误差影响较大的设计参数,通过设计参数修正法确定其修正量,对初始有限元模型进行准确修正.
1 模型修正基本理论
任何结构都是由刚度、质量、阻尼三个物理特性组成的系统,则可建立结构振动微分方程
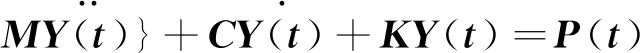
(1)
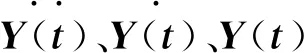
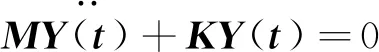
(2)
设上述方程的解的形式为
y=Ysin(fit+α)
(3)
代入式(2):消去公因子sin(fit+α),即得
(4)
上述是位移幅值的齐次方程,为了得到Y的非零解,应使系数行列式为0,即
(5)
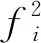
(6)
式(6)与式(5)的解可以展开为一个一元高次方程,在有限元模型中,结构的固有频率和固有振型与它的质量矩阵和刚度矩阵有关.结构有限元模型修正步骤见图1.
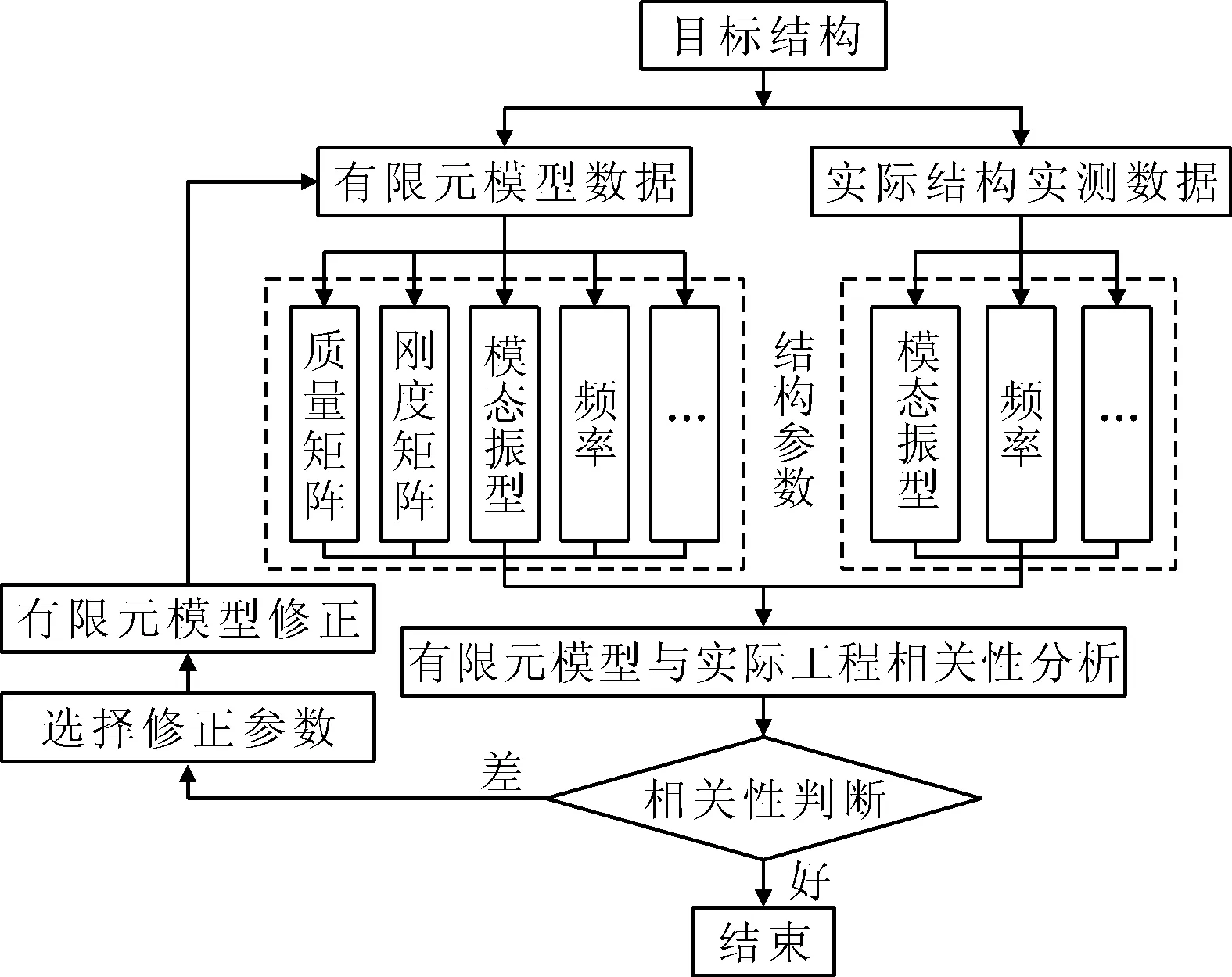
图1 结构有限元模型修正的基本步骤
2 设计参数灵敏度分步修正
2.1 灵敏度分析
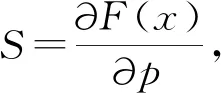
(7)
对式(7)左乘YiT
(8)
对式(4)进行转置:
(9)
根据模态振型的正交性
YiTMYi=1
(10)
YiTKYi=1
(11)
将式(9)~(10)与式(11)代入式(8)中,则待修正参数p对结构第i阶固有频率的灵敏度为
(12)
式(12)即为结构的设计参数p对结构第i阶固有频率的灵敏度计算方法,经过灵敏度分析,找出对结构固有频率灵敏度影响较大的设计参数,再对其进行排序并依次对结构的有限元模型进行合理的修正.但是如何确定修正量,这就涉及到设计参数法了.
2.2 设计参数法
设计参数修正法是根据结构的设计参数(如面积、高度,以及弹性模量、密度、泊松比等)对结构进行一定的修改,从而使得修正后结构的静动力特性更加接近结构的真实值.对于梁式结构,建立由n个自由度组成的有限元模型,其中质量矩阵为M,刚度矩阵为K,结构第i阶固有频率为fie,结构第i阶固有振型为Yie.设结构设计参数经过修正后的第i阶固有频率为fia,结构第i阶固有振型为Yia.
为了得到结构设计参数的修正量,将修正后模型的固有频率fia作为这些参数的目标函数,在其初始值p处按照泰勒公式展开.
(13)
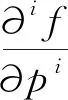
(14)
式中:Δp为结构设计参数的修改量,对于实际工程结构,只需要考虑参数的微小变化,可以忽略高阶的影响,仅考虑一阶泰勒展开对式(13)与式(14)得
(15)
式中:pj为第j个欲修改的参数,要使得修正后的有限元模型的固有频率fia与实测结构的固有频率fie一致,则必须保证两者之间误差最小.将式(15)变形得
(16)
即设计参数得修改量为
(17)
对以上方程进行线性求解即可得到结构设计参数Δp的具体修改量,再加上初始值即可得到修改后的设计参数.选定的待修正参数必须对结构的固有频率反应敏感,且便于修正.结构固有频率与参数之间灵敏度的关系复杂,不仅同一阶次频率对不同参数的灵敏度存在差异,不同阶次频率对同一参数的灵敏度同样存在差异.因此,需要对设计参数的灵敏度进行排序,剔除灵敏度低的参数,将灵敏度高的参数保留作为待修正参数.图2为待修正参数的选择过程.
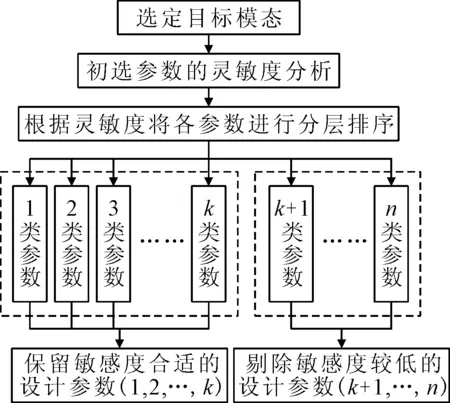
图2 待修正参数的选择过程
2.3 相关性分析
目前基于动力的相关性分析一般都利用结构的实测频率和计算频率做相关性分析,采用的相关性计算公式见式(7).误差精度为
(18)
式中:ωie为计算自振频率;ωia为测试自振频率;i为结构对应阶次;p为相应的设计参数.对于工程而言,要求-5%≤ε≤5%,ε绝对值越小,说明修正效果越好.
3 数值模拟
3.1 初始模型的建立
现以一悬臂梁为基本模型,选用其固有频率作为目标模态,模拟灵敏度法修正结构模型误差的过程.悬臂梁的参数如下:全长l=1.8 m,截面宽度b=60 mm,高度h=10 mm,弹性模量E=206 GPa,密度ρ=7.85×10-6kg/mm3.将悬臂梁结构的有限元模型分为30个单元,每个单元长度60 mm.
根据结构材料与刚度之间的关系,通过折减弹性模量的方式模拟单元发生裂缝损伤的工况.将实际结构的运营状况预设为以下两种工况(假设为实测频率).
工况1 结构在单元3、10、17、24处材料的弹性模量依次减少10%、30%、50%、70%,其他参数保持不变.
工况2 结构在单元2、7、12、17、22、27处材料的弹性模量依次减少10%、20%、30%、40%、50%、60%,其他参数保持不变.
3.2 有限元结果分析
将悬臂梁结构的原始参数建立有限元模型作为初始模型,工况1、工况2作为悬臂梁的实测响应.实测频率与初始模型前10阶固有频率的相对误差见表1.
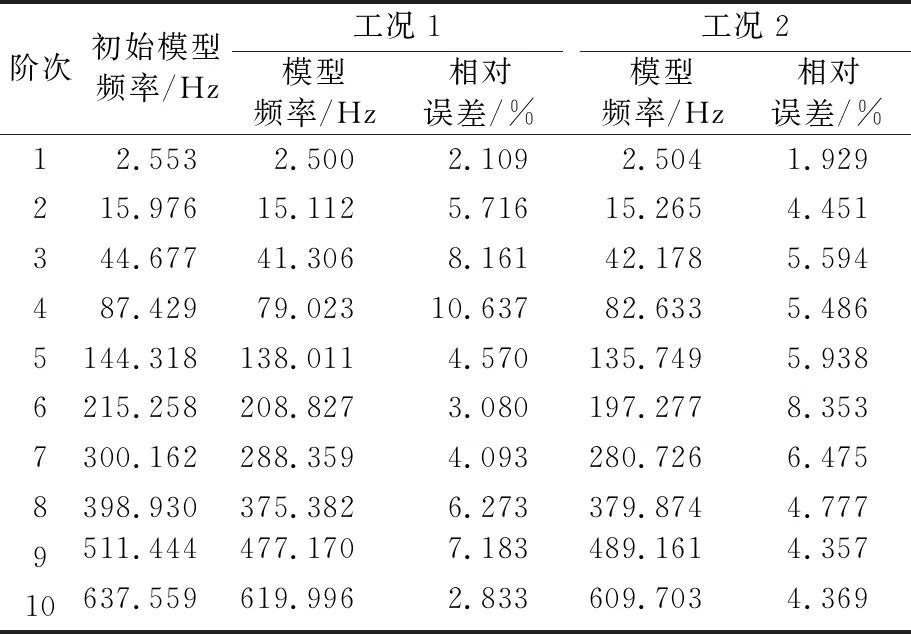
表1 有限元模型固有频率与结构实测频率(模拟假设)
3.3 灵敏度分析
对于复杂结构的设计参数较多,包含截面尺寸、弹性模量、密度以及边界条件等.不同的参数类型的量纲和量级对目标参数的影响都不同,现以固有频率对设计参数的灵敏度为例,说明不同量纲和量级对固有频率灵敏度的影响.

表2 不同设计参数初始值及灵敏度比较
由表2可知,不同类型的设计参数灵敏度结果分析的量纲不同,当设计参数的微小变化(如同等单位改变量的密度和弹性模量)不足引起梁结构发生较大的变化.因此当设计参数的量纲和量级不统一时,各设计参数的灵敏度不具有可比性,难以难以判断设计参数的灵敏度程度,同时也不利于设计参数的取值.
为解决设计参数的灵敏度量纲与量级之间的差异,现利用固有频率变化比ε与设计参数变化比P代替中的∂fi、P.则灵敏度的表达式为
(19)
式(18)中固有频率的变化率ε与固有频率、设计参数的变化率P与设计参数本身具有相同的性质,从而结构固有频率关于设计参数的灵敏度量纲得以统一.即各参数在微小变化P下,引起的固有频率变化不会因为设计参数的量纲与量级而产生误差.
3.4 设计参数修正
由式(12)对悬臂梁结构有限元模型各参数进行分析,得出对该悬臂梁结构的固有频率较为敏感的参数主要有:材料参数(密度ρ,弹性模量E),尺寸参数(截面宽度b、高度h).选取弹性模量和密度作为结构参数设计变量,根据式(19)(假设上限为10%),通过midas Civil有限元软件计算出密度的灵敏度值为-0.541(随着密度的增大,固有频率减小),弹性模量的改变量为0.514(弹性模量的增加,固有频率变大).
在对设计参数进行修正时,若修改参数过少,必然会造成该修改参数的修改量过大,这往往与实际不相符合.且结构固有频率往往是由于多个设计参数相互影响而造成,因此应该首先选择灵敏度值较大的密度作为修正参数对结构的初始有限元模型进行修正,再对弹性模量依次进行迭代修正,直至模型的固有频率误差在合理范围.密度与弹性模量修正量与结果分别见表3~7.
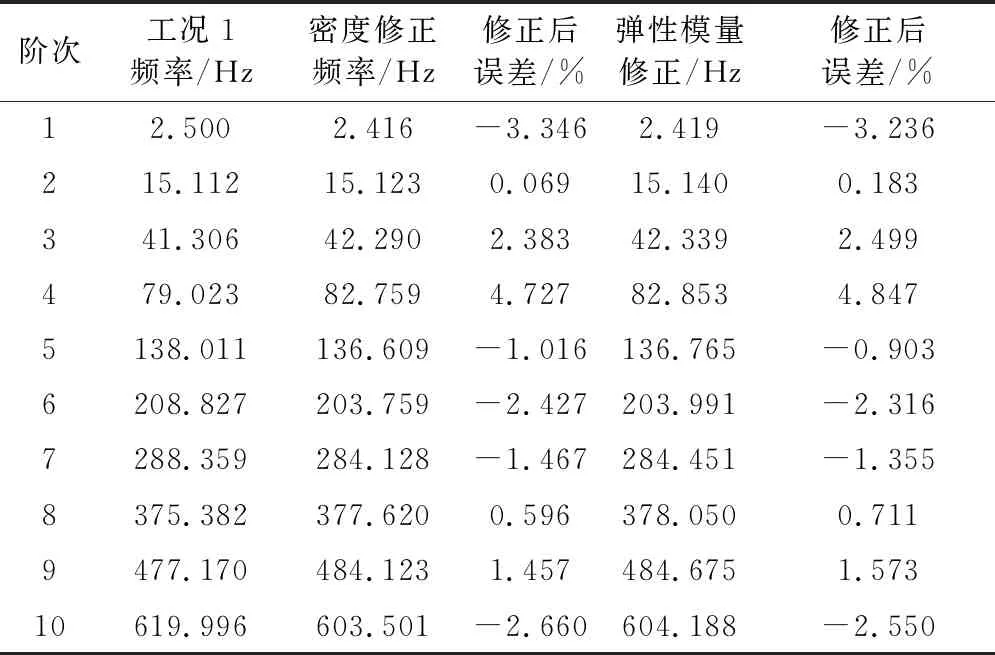
表3 工况一悬臂梁模型密度、弹性模量单独迭代修正结果
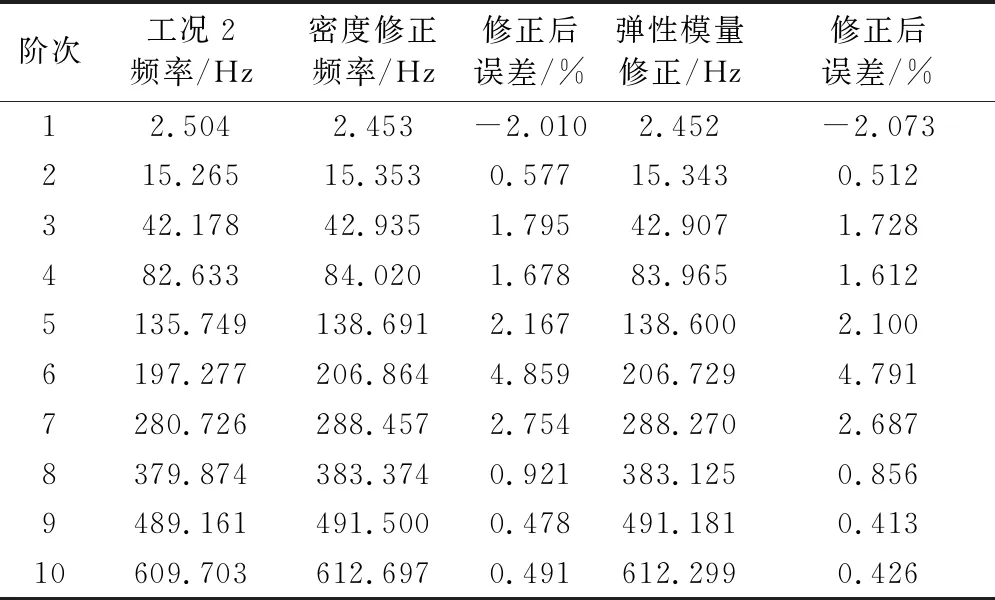
表4 工况二悬臂梁模型密度、弹性模量单独迭代修正结果
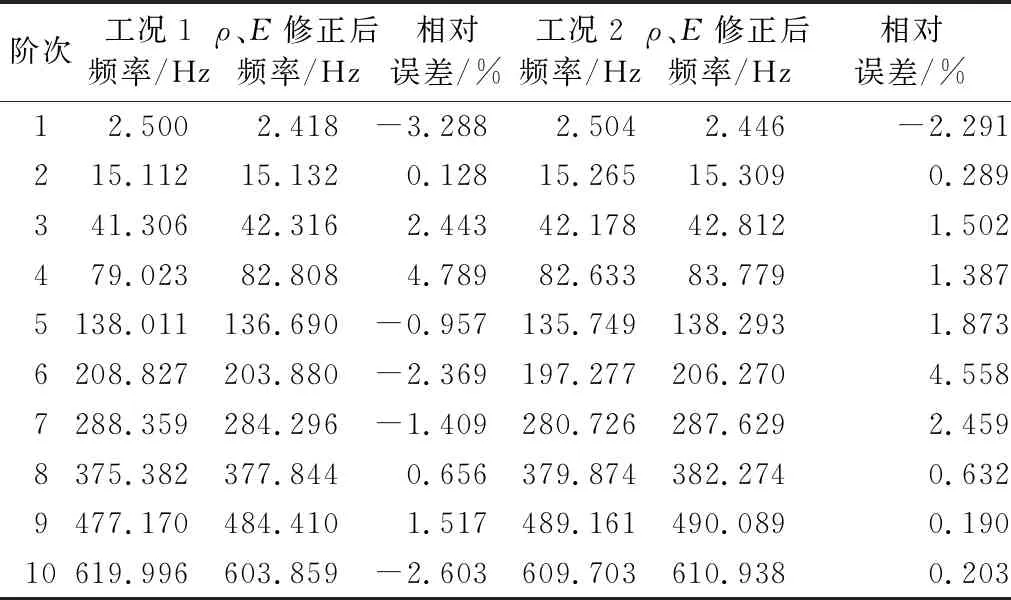
表5 悬臂梁模型密度、弹性模量同时迭代修正结果
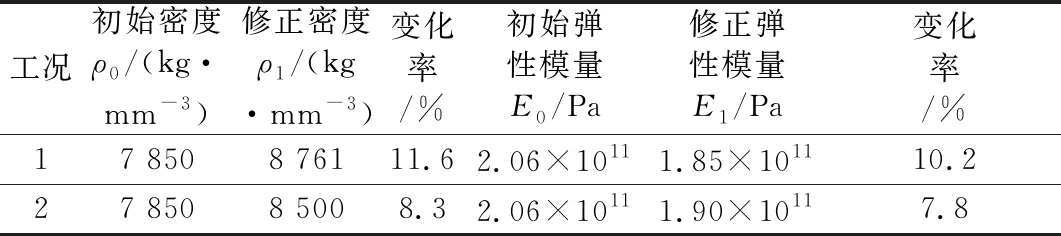
表6 悬臂梁模型密度、弹性模量单独迭代修正变化量
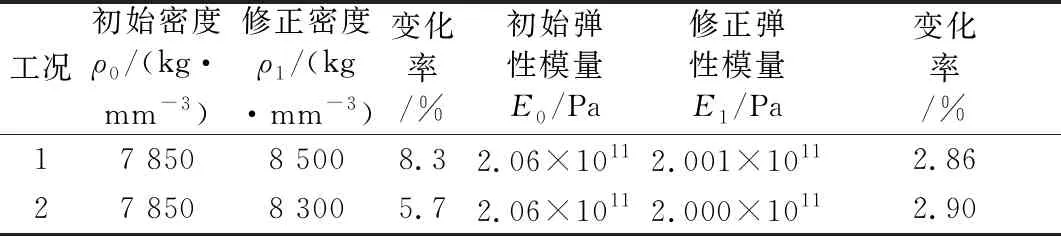
表7 悬臂梁模型密度、弹性模量迭代修正变化量
对悬臂梁结构设计参数(密度与弹性模量)的修正结果表明:
1) 在统一结构固有频率对设计参数的灵敏度量纲后,选取密度与弹性模量作为修改量,使得修改后悬臂梁的计算固有频率与实测频率十分相近,从而验证了灵敏度设计参数法的正确性.
2) 将密度与弹性模量同时对悬臂梁分步迭代的修正方法,相比单独迭代修正法,修改量更小,修正精度更高.
4 结 论
1) 当结构初始建立的有限元模型所得到的静动力学响应与结构的实测的静动力学响应相差较大时,将设计参数法与灵敏度分析法相结合起来,能快速、高效的对结构有限元模型精准修正,从而为桥梁健康监测与损伤识别提供良好依据.
2) 在采用设计参数灵敏度法时,设计参数的量纲与量级不同会到影响模型修正的效果.将灵敏度统一量纲后,能减小结构目标模态的修正误差.
3) 结构的目标模态往往受多个设计参数的影响,在进行模型修正时,若选取修正参数数量过少,会导致参数修正量过大且修正精度偏低,应选取多个参数进行迭代求解.
猜你喜欢
——以匀加速直线运动公式为例
