基于FFT奇异值分解的光谱信号去噪算法

朱红求,程 菲，胡浩南，周 灿,2*,李勇刚

1.中南大学自动化学院,湖南 长沙 410083 2.高性能复杂制造国家重点实验室,湖南 长沙 410083

引 言

微型光谱仪是由光源、测量附件和光纤构建的光学测量系统[1]，其具有模块化和高速采集的特点。微型光谱仪在采集光谱数据时，特别容易受到电子元件组成电路噪声的影响，比如，暗电流散粒噪声、光子散粒噪声、复位噪声、读出噪声等等[2]。噪声在光谱信号采集、信号调理、传输过程中逐步渗透到真实光谱信号中，并且会在一定波长处出现光源特征峰，这无疑会对后期的数据分析产生巨大的影响。为提高信号信噪比和还原真实光谱信号图谱特征[3]，在将采集到的光谱数据进行模型预测之前，对光谱信号进行预处理，从而提高光谱信息定量分析的稳健性和准确性显得尤为重要。

到目前为止，对光谱数据降噪，国内外众多研究者已经进行了大量的研究工作，有自适应滤波算法[4]、SG平滑滤波[5]和小波变换[6]等，但是不同的去噪算法仍然具有各自的局限性，尤其是传统的去噪算法会将光谱信号中具有图谱特征的突变细节滤除或者信号容易出现延时和失真。奇异值分解[7](singular value decomposition,SVD)具有无延时、相移小等特点，并且选取到合适的奇异值分解的阶次可以使光谱信号的图谱特征得到很好地保留。张莹等提出用峭度和包络熵指标构成综合评价指标对重构矩阵的秩进行优化，根据综合评价指标值最优确定信号重构的阶次[8]，赵学智等提出了基于差分谱理论来确定有用分量的个数[9]，代荡荡等[10]利用模糊C均值聚类算法对奇异值降噪阶次选取进行了改进,但是上述的量化判据方法在处理多重金属离子紫外可见光谱信号时容易导致选取的奇异值降噪阶次偏小而过降噪。Zheng等提出了一种多级奇异值分解降噪算法[11]，该判据方法对多重金属离子紫外可见光谱信号处理后仍保留部分噪声，导致去噪性能欠佳。

为此，本文提出了一种基于奇异值重构信号分量频率的光谱信号去噪算法。本算法根据每个奇异值分量信号快速傅里叶变换结果中振幅最大所对应的频率值，然后按照奇异值递减方式对相应分量信号频率值进行一阶滞后差分，得到频率差分谱。选择差分谱第一个谱峰值大于设定阈值处所对应的奇异值即为奇异值分解降噪的有效阶次。

1 奇异值分解去噪

假设有含噪信号X=(x1,x2,…,xN)，其中原始信号S=(s1,s2,…，sN),噪声信号V=(v1,v2,…，vN)，N为信号的长度，并且满足

X=S+V

(1)

按照式(2)将含噪信号X构造成m×n(m≤n)的Hankel矩阵

(2)

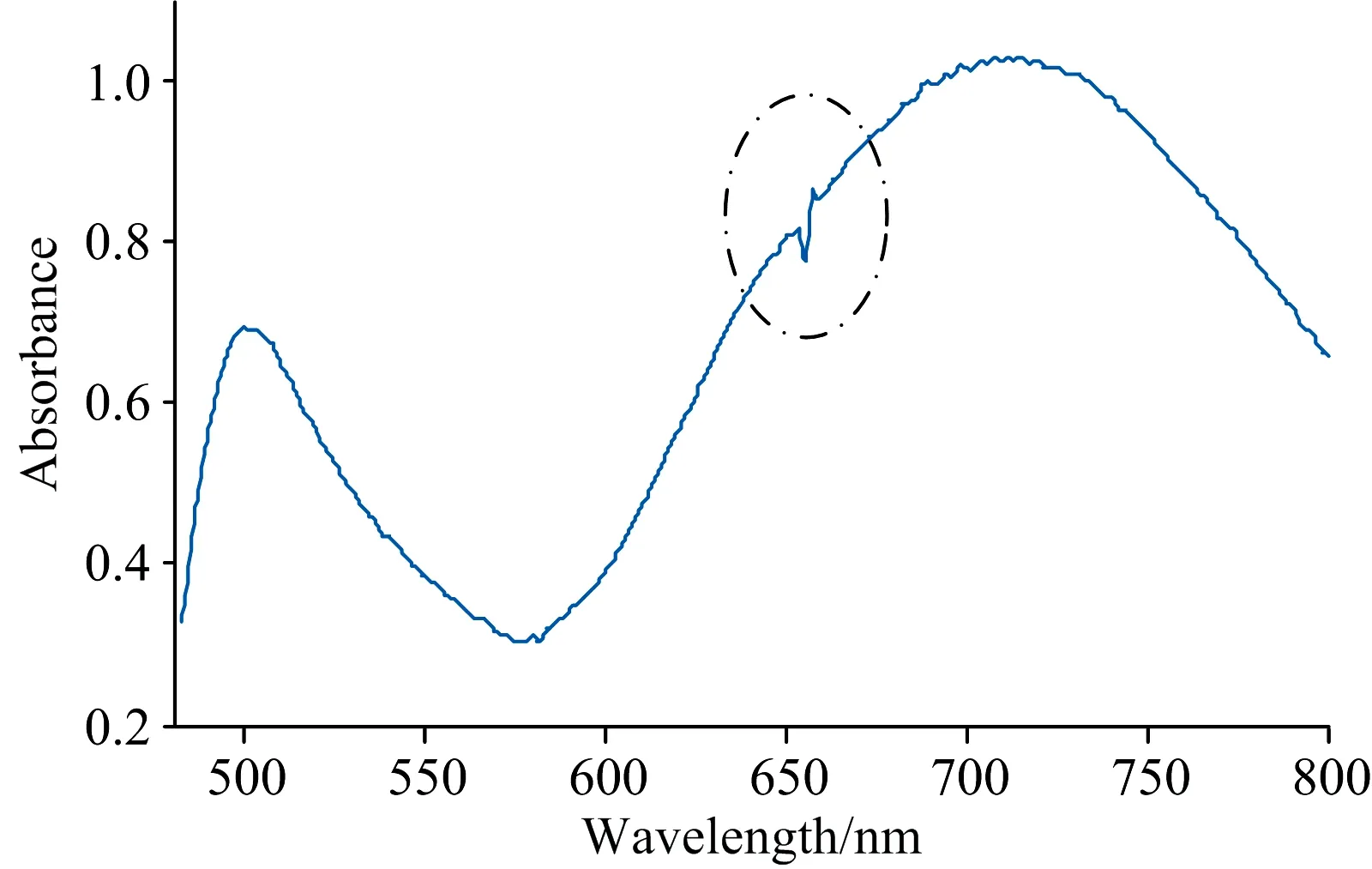
其中1

将得到的Hankel矩阵进行奇异值分解

H=UΣVT

(3)

其中，U=(u1，u2，…，um)∈Rm×m，V=(v1，v2，…，vm)∈Rn×n均为正交矩阵，Σ为m×n维矩阵。

(4)

其中Λ=diag(σ1，σ2，…，σr),并且σ1≥σ2≥…≥σr，σi为矩阵H的奇异值，r为Hankel矩阵的秩，0为零矩阵。

奇异值分解降噪的原理是通过取矩阵Λ的前k(k

2 奇异值分解阶次选取方法的研究

为保证信号去除噪声的同时，尽可能的保留信号的图谱特征，本文提出了一种新的有效的奇异值分解阶次选取的算法。

(5)

(6)

步骤3：将步骤2中得到的r个分量信号分别作快速傅里叶变换，即可得到每个信号分量快速傅里叶变换结果中振幅最大所对应的频率值。

步骤4：按照奇异值递减方式对相应分量信号频率值进行一阶滞后差分，得到主频差分谱，选择差分谱第一个谱峰值大于所设阈值(预设差分阈值范围为[30,50])所对应的奇异值作为奇异值分解降噪的有效阶次。

步骤5：根据步骤4所得到的有效阶次，再将剩余奇异值置零，再反演重构得到去噪后的光谱信号。

3 实验结果与讨论

以湿法炼锌为背景，配置Zn2+，Co2+，Cu2+和Fe3+浓度分别为33 g·L-1，4 mg·L-1，12 mg·L-1和6 mg·L-1的混合标准溶液，使用北京普析通用仪器的T9双光束紫外可见分光光度计，扫描波长为0.5 nm，扫描范围为480～800 nm，混合溶液的实测紫外可见光谱信号如图1所示。为了验证本文算法对紫外可见光谱信号的去噪的优越性和有效性，我们对实测紫外可见光谱信号添加不同强度的随机噪声，得到信噪比在[12.4,32.4]区间内的仿真信号，单位为dB，仿真数据总样本量为55，其中图2为信噪比为20 dB的含噪仿真光谱信号。

图1 原始光谱信号Fig.1 Original spectral signal

将图2信号构造为m×n的Hankel矩阵，其中m的取值为320，n的取值为321。将其SVD，在对前8个奇异值反演求得相应奇异值分量信号，如图3、图4所示。

图2 信噪比为20 dB的含噪仿真光谱信号Fig.2 Simulation spectral signal with noise ratio of 20 dB

图3 信噪比为20 dB含噪信号前4个奇异值分量信号分布图Fig.3 Signal distribution diagram of the first four singular value components of noisy signal with signal-to-noise ratio of 20 dB

图4 信噪比为20 dB含噪信号第5至8个奇异值分量信号分布图Fig.4 Signal to noise ratio is 20 dB,the fifth to eighth singular value component signal distribution diagram of noisy signal

由于每一个奇异值分量信号都具有原始噪声信号的特征，并且前k个奇异值分量信号之和代表着理想真实信号，从图2和图3中我们发现，当随着奇异值的增大，奇异值分量信号的频率会有一个突变，相较于平稳变化点而言，突变点往往携带了更重要信息，对于选择奇异值阶次，第一个较大突变点需要格外关注，这时我们可以认为频率突变点前k个奇异值即为我们需要选取的奇异值分解的阶次。

对前50个奇异值分量信号分别作快速傅里叶变换，即可得到每个信号分量快速傅里叶变换结果中振幅最大所对应的频率值，然后按照奇异值递减方式对相应分量信号频率值进行一阶滞后差分，得到主频差分谱，选择差分谱第一个谱峰值大于50所对应的奇异值作为奇异值分解降噪的有效阶次。如图4所示，我们选取前50个奇异值分量信号主频差分谱。

从图5中我们发现差分谱第一个谱峰值大于所设阈值50所对应的奇异值在第6个，因此该仿真含噪信号奇异值分解降噪的有效阶次为6。

图5 前50个奇异值分量信号主频差分谱Fig.5 Main frequency difference spectrum of the first 50 singular value component signals

为了进一步验证本文所提奇异值分解降噪算法的有效性，我们选择奇异值差分谱算法、小波去噪算法、SG滤波算法同本文所提算法在提高信号信噪比和减少信号均方根误差性能方面作了对比分析，其中SG去噪算法窗口宽度选择9，多项式拟合次数选择2次，小波去噪算法选择“db4”作为小波基函数，同时进行4层分解。选择50组不同信噪比的仿真数据对比，本文所提算法相较于SG滤波算法和小波变换去噪算法信噪比分别提高了22.05%，10.88%，均方根误差分别降低了74.28%，41.29%，而奇异值差分谱算法对部分信噪比的紫外可见光谱信号并无明显去噪能力，对比结果如图6和图7所示。

图6 不同算法去噪后的信噪比Fig.6 SNR after denoising by different algorithms

图7 不同算法去噪后的均方根误差Fig.7 Root mean square error after denoising by different algorithms

为进一步验证本文算法对真实紫外可见光谱信号的去噪能力，以湿法炼锌为背景，配置Zn2+，Co2+，Cu2+，Fe3+和Ni2+浓度分别为33 g·L-1，1 mg·L-1，1.2 mg·L-1，1 mg·L-1和1.4 mg·L-1的混合标准溶液，使用厦门奥谱天成微型光谱仪扫描波长为0.4 nm，扫描范围为480～800 nm，混合溶液的实测紫外可见光谱信号如图8所示。

图8 实测光谱信号Fig.8 Measured spectral signal

如图9—12所示,通过观察虚线框中的去噪后的信号，本文算法不仅有效地去除了噪声并且将光源特征峰干扰信号基本滤除，而奇异值差分谱算法得到的去噪后信号发生失真，SG滤波算法和小波变换去噪算法虽然可以起到信号平滑作用，但是也未能将光源特征峰干扰信号滤除，在一定程度影响光谱信号定量分析的精确性。

图9 本文算法对实测光谱信号降噪效果Fig.9 The denoising results of the simulation data with the algorithm in this paper

图10 奇异值差分谱算法对实测光谱信号降噪效果Fig.10 The denoising results of the simulation data with the singular value difference spectrum algorithm

图11 SG滤波算法对实测光谱信号降噪效果Fig.11 The denoising results of the simulation data with the SG filtering algorithm

图12 小波变换去噪算法对实测光谱信号降噪效果Fig.12 The denoising results of the simulation data with the denoising algorithm of wavelet transform

4 结 论

提出了一种基于奇异值重构信号分量频率的光谱信号去噪算法。本算法根据每个奇异值分量信号快速傅里叶变换结果中振幅最大所对应的频率值，然后按照奇异值递减方式对相应分量信号频率值进行一阶滞后差分，得到频率差分谱。选择差分谱第一个谱峰值大于设定阈值处所对应的奇异值即为奇异值分解降噪的有效阶次。最后通过对比表明，本文所提算法相较于奇异值差分谱算法、SG滤波算法和小波变换去噪算法在处理真实紫外可见光谱信号中不仅抑制了噪声影响，能更好提高信号的信噪比和减小均方根误差，而且将微型光谱仪的光源特征峰有效滤除，在紫外可见光谱信号的定量分析中具有较好的应用前景。