基于键极化加和模型及其实验修正方法的超拉曼微观极化率张量元微分的简化方案-C2v对称性

汪 源，张 贞，郭 源

1.三亚学院理工学院，海南 三亚 572022 2.北京分子科学国家研究中心,中国科学院化学研究所，北京 100010 3.中国科学院大学化学科学学院，北京 100049

引 言

近十几年来，相干反斯托克斯拉曼光谱(Coherent Anti-Stokes Raman spectroscopy,CARS)及其表面增强方法[1-4]以及相干反斯托克斯超拉曼光谱(Coherent Anti-Stokes hyper-Raman spectroscopy,CAHRS)[5-7]等高阶非线性光谱技术在动力学过程、基因表达谱筛选、高分辨率光谱技术等方面得到重要的应用。然而上述研究仅仅对光谱信号进行定性分析，缺乏对光谱信号进行定量分析。这在某种程度上限制了其应用。作为高阶非线性相干光学过程，CARS和CAHRS的光谱信号由分子基团的三、四阶微观极化率张量元贡献[8]，对于n阶非线性相干光谱，分子微观极化率张量元的数量为3n+1个，例如CARS涉及81个分子微观极化率张量元。这些数量众多的分子微观极化率张量元将导致对高阶非线性相干光学过程进行定量分析存在着较大的困难[8]。加之作为高阶非线性相干光学过程，CARS和CAHRS的实验条件较为苛刻，为了便于分析结果，目前使用较多的实验构型为垂直入射式[2]。但随着对高阶非线性光学过程理论的深入研究和高阶非线性光学技术的发展，实验技术和实验方法将会逐渐完善，非垂直入射的非共线实验构型的情况下，高阶微观极化率张量元的获得对光谱信号定量分析尤为重要。

1 BAM求解单键的

图1 C∞v对称性分子基团的分子坐标系Fig.1 Molecular coordinate system of C∞v symmetric molecular group

单键AB的折合质量GA1和对称振动模式的简正坐标QA1定义如式(1)和式(2)[14]

GA1=1/MA+1/MB

(1)

(2)

式(1)和式(2)中MA和MB为原子A和B的质量，Δr为AB沿着键坐标系(ξ,η,ζ)中ζ轴的振动矢量。从表达式(1)和式(2)可得式(3)

(3)

对于AB，分子坐标系(a,b,c)与键坐标系(ξ,η,ζ)完全重合，因此振动矢量Δr在分子坐标系中的投影分量分别在式(4)中表达

(Δr)a=0，(Δr)b=0，(Δr)c=|Δr|

(4)

AB的超拉曼微观极化率张量元微分之间的关系如式(5)

(5)

μξ=β0(r2EζEξ+r2EξEζ)Δζ=2β0r2EξEζΔζ

(6)

μη=β0(r2EζEη+r2EηEζ)Δζ=2β0r2EηEζΔζ

(7)

μζ=β0(r1EξEξ+r1EηEη+EζEζ)Δζ

(8)

其中Eξ，Eη和Eζ分别为外界光场在键坐标系中的投影。将式(6)—式(8)变换到分子坐标系，得

μa=β0(r2EcEa+r2EaEc)|Δr|=2β0r2EaEc|Δr|

(9)

μb=β0(r2EcEb+r2EbEc)|Δr|=2β0r2EbEc|Δr|

(10)

μc=β0(r1EaEa+r1EbEb+EcEc)|Δr|

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

2 BAM求解分子基团AB2的

对于图2所示的具有C2v对称性的分子基团AB2，简正模式的折合质量GA1和GB1如式(20)和式(21)定义[14]

图2 C2v对称性分子基团的分子坐标系Fig.2 Molecular coordinate system of C2v symmetric molecular group

GA1=(1+cosτ)/MA+1/MB

(20)

GB1=(1-cosτ)/MA+1/MB

(21)

其中τ为AB2的键角。简正坐标QA1和QB1的定义如式(22)和式(23)[14]

(22)

(23)

其中|Δri|为单键ABi(i=1,2)沿着各自键坐标系(ξi,ηi,ζi)中ζi轴的振动矢量Δri的模。从式(22)和式(23)可得式(24)和式(25)

(24)

(25)

振动矢量Δr1和Δr2在分子坐标系中的投影分量分别为式(26)和式(27)

(26)

(27)

按照分子基团偶极矩的定义，单键ABi(i取1,2)在键坐标系中偶极矩的三个分量表达式见式(28)—式(30)

μξi=β0(r2EζiEξi+r2EξiEζi)|Δri|=

2β0r2EξiEζi|Δri|

(28)

μηi=β0(r2EζiEηi+r2EηiEζi)|Δri|=

2β0r2EηiEζi|Δri|

(29)

μζi=β0(r1EξiEξi+r1EηiEηi+EζiEζi)|Δri|

(30)

键AB1和AB2除了取向以外完全相同，所以两个单键皆具有相同的β0，r1和r2；Eξi，Eηi和Eζi为外界光场在各自键坐标系中的投影，从其表达式为(见图2)式(31)和式(32)

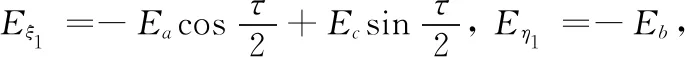
(31)

(32)

将两个单键的偶极矩投影到分子坐标系中并加和，可得式(33)和式(34)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

由|Δr1|和|Δr2|的式(24)和式(25)可知

(46)

(47)

(48)

(49)

(50)

(51)

(52)

(53)

(54)

(55)

(56)

3 AB2分子基团的实验修正

图3 超拉曼光谱实验光路图Fig.3 Experimental light road of Hyper-Raman spectroscopy

(57)

(58)

(59)

(60)

将实验测量的ρHR-SS和ρHR-AS代入式(59)和式(60)中即可得CH单键的r1和r2值。

与处理拉曼微观极化率张量元微分相同[14]，在处理不同对称振动模式的超拉曼微观极化率张量元微分比值时需要结合同一偏振组合的超拉曼光谱的实验数据对BAM方法进行进一步修正。例如对于乙烯的CH2分子基团，HV偏振组合时对称振动模式和反对称振动模式的超拉曼光谱强度比值见式(61)

(61)

(62)

结合式(61)和式(62)可得式(63)

(63)

4 结 论