复杂形状钣金型材截面参数化方法研究
2022-01-12陈英华
陈英华,王 影
(中国直升机设计研究所,江西 景德镇 333001)
0 引言
作为直升机结构中最常用的构型形式,钣金型材常被用于框梁凸缘、平台长绗、加强立筋等结构,其与蒙皮组成的壁板加筋结构也是传统航空器结构设计中效率最高和应用最多的结构形式。在强度分析时,型材的截面参数是个关键的设计输入,在进行有限元分析时不可忽略,特别是动力学分析。截面形状的差异对模型的刚度和重量分布具有重要影响。因此,为了模拟真实结构,有限元建模时需要对型材的截面形状进行精确定义。
关于航空结构参数化方法的研究,早期较多是基于CAD系统,采用数值技术,开发了有限元软件,建立了常用型材的标准数据库,大幅提高了建模效率[1-2]。随着有限元技术的发展,学者们对结构参数化方法进行了更多的探索。基于不同的商用软件平台,复杂结构参数化建模技术广泛应用于船舶设计[3]、锅炉设计[4-5]、机械制造[6-7]以及航空设计与制造[8-10]等领域。
目前的主流有限元商用软件中,截面定义多采用参数化的方法,通过给定几个常用规则截面,用户可以输入长度、厚度等参数,用于计算截面的所有轮廓点坐标和属性参数。但是,为了便于编程和标准化,参数化时普遍不考虑倒角,将倒角处理为直角。这与实际结构差异较大,特别是倒角较大时,带来的差异不可忽略。另外,模块化的参数化方法往往局限于规则截面,对于航空结构上大量的非规则截面,尚无普适的参数化方法。
针对上述不足,本文开展了考虑倒角的任意钣金型材截面参数化方法研究,并基于MSC.Patran软件平台,开发了相应的模块程序,用于非规则截面的参数化定义;最后通过算例验证,该方法可用于复杂工程结构的有限元精确模拟。
1 参数化方法
对于型材截面形状,参数化方法一般分为中心线定义法和轮廓描点法。为了考虑不规则截面的普适性以及倒角形状,本文采用轮廓点定义的方法进行参数化,即以截面的所有轮廓点坐标为目标函数,建立输入基本参数与目标函数的关系。
为了便于标准化和模块化,首先假设钣金型材的截面为等厚度,且采用统一的倒角角度,考虑带倒角的钣金型材的几何特征,设置输入的基本参数为:
1)截面的边数N;
2)钣金的厚度t;
3)钣金的倒角半径r;
4)边的长度L1,L2,…,LN;
5)相邻边之间的角度θ1,θ2,…,θN-1(|θi|<180);
6)旋转角度θr。
1.1 倒角弧
以任一自由边的端点为原点,起始边为X横轴,建立平面局部坐标系,如图1所示。
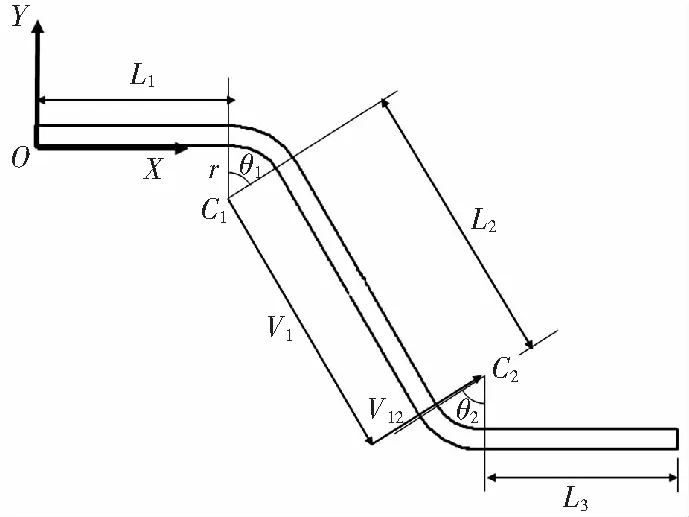
图1 局部坐标系示意
设起始点坐标为(0,0),则第一个倒角的圆心坐标的表达式为:
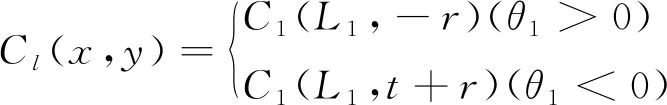
(1)
其中,θ1表示以边L1和L2的交点为圆心,从边L1位置旋转到边L2位置所需的角度,定义正为逆时针,负为顺时针。
根据(1)式就得到第一个倒角的圆心坐标。同时,为了计算倒角弧的轮廓坐标,需要计算倒角弧的方位角。建立的倒角弧局部坐标如图2所示。

图2 倒角弧方位角示意
从图2可知,当倒角弧为顺时针方向时,根据几何关系,倒角弧的起始和终止方位角A1-start和A1-end可以表示为:
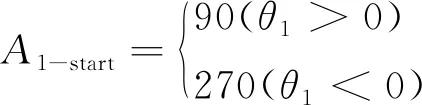
(2)
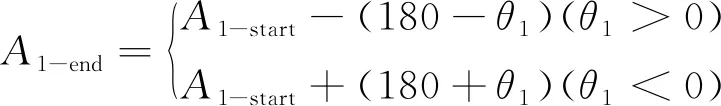
(3)
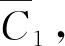
C1={C1(x,y),r,A1-start,A1-end}
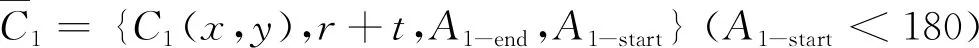
(4)
或
C1={C1(x,y),t+r,A1-start,A1-end}
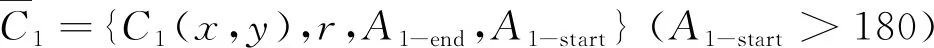
(5)
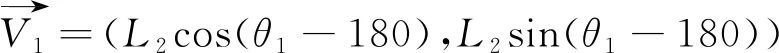
(6)
根据上式,可以得到第二个倒角弧的初始圆心。此时,第二倒角弧的初始圆心与第一个倒角弧为同侧。然后需要判断θ2与θ1的关系,若θ2θ1>0,则表示第二个倒角弧为同侧,不需要再进行镜像;若θ2θ1<0,则需要镜像到另侧。根据几何关系,镜像矢量为:
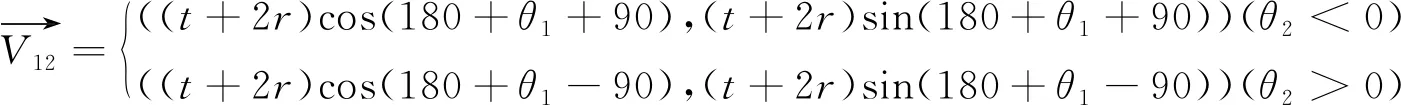
(7)
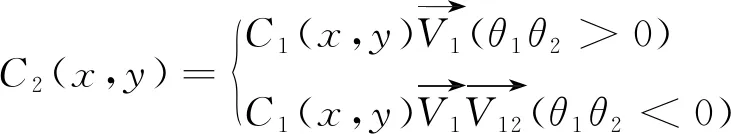
(8)
根据上式可以求解得到第二个倒角弧圆心坐标。同理,倒角弧的方位角可以表示为:

(9)
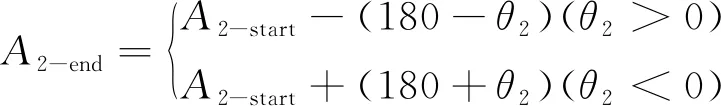
(10)
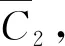
C2={C2(x,y),r,A2-start,A2-end}
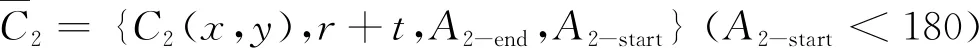
(11)
或
C2={C2(x,y),t+r,A2-start,A2-end}
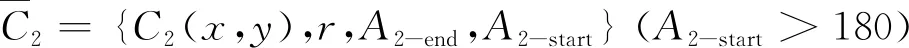
(12)

(13)
重复上述步骤,可以依次计算得到所有倒角弧圆心坐标参数集对:
Ci={Ci(x,y),r,Ai-start,Ai-end}
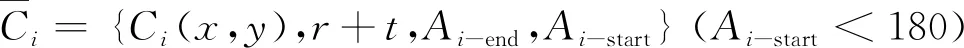
(14)
或
Ci={Ci(x,y),r+t,Ai-start,Ai-end}
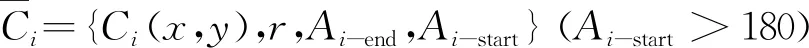
(15)
1.2 轮廓点矩阵
为了提高精度,采用5个点等角度对每个倒角弧进行平均离散。依据前文建立的圆心坐标参数集,依次计算每一个倒角弧5个离散点的坐标:
CPi=[P1P2P3P4P5]
(16)
对于每个点坐标,可表示为:
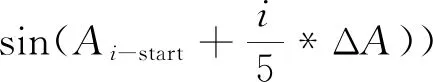
(17)
ΔA=Ai_end-Ai_start
(18)
然后,从原点出发,对截面的所有轮廓点进行排序。轮廓及坐标点示意图见图3。

图3 轮廓点序列示意
按逆时针方向,所有轮廓点的组合序列[S]为:
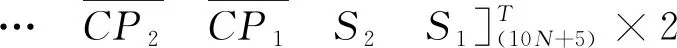
(18)
其中,S1、S2、E1、E2为截面的四个端点,最终组成了轮廓点坐标总矩阵。根据实际截面形状,可以对上述的轮廓点进行旋转角度,总的坐标总矩阵转置矩阵[T]可以表示为:
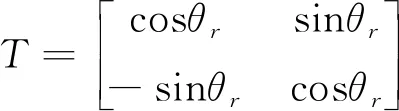
(19)
[ST]=[S][T]
(20)
最后,根据上一步的所有轮廓点坐标结果[ST],采用数学积分的方法,可以计算出截面的面积、形心、惯性矩等截面属性,或者直接应用商用软件的内置计算模块进行求解。
2 软件实现
PCL语言为Patran软件内置的用户二次开发语言,可用于基于该软件平台的界面开发、参数及内部函数调用等功能开发。用户通过自定义程序和界面设计,可以实现参数化、模块化及多样化的应用。
为了提高效率,本文采用PCL语言,基于上述算法,开发了直升机复杂形状钣金型材截面设计模块。程序模块主要分为参数输入、倒角弧圆心坐标、轮廓点矩阵等功能,流程图和典型算例界面如图4和图5所示。
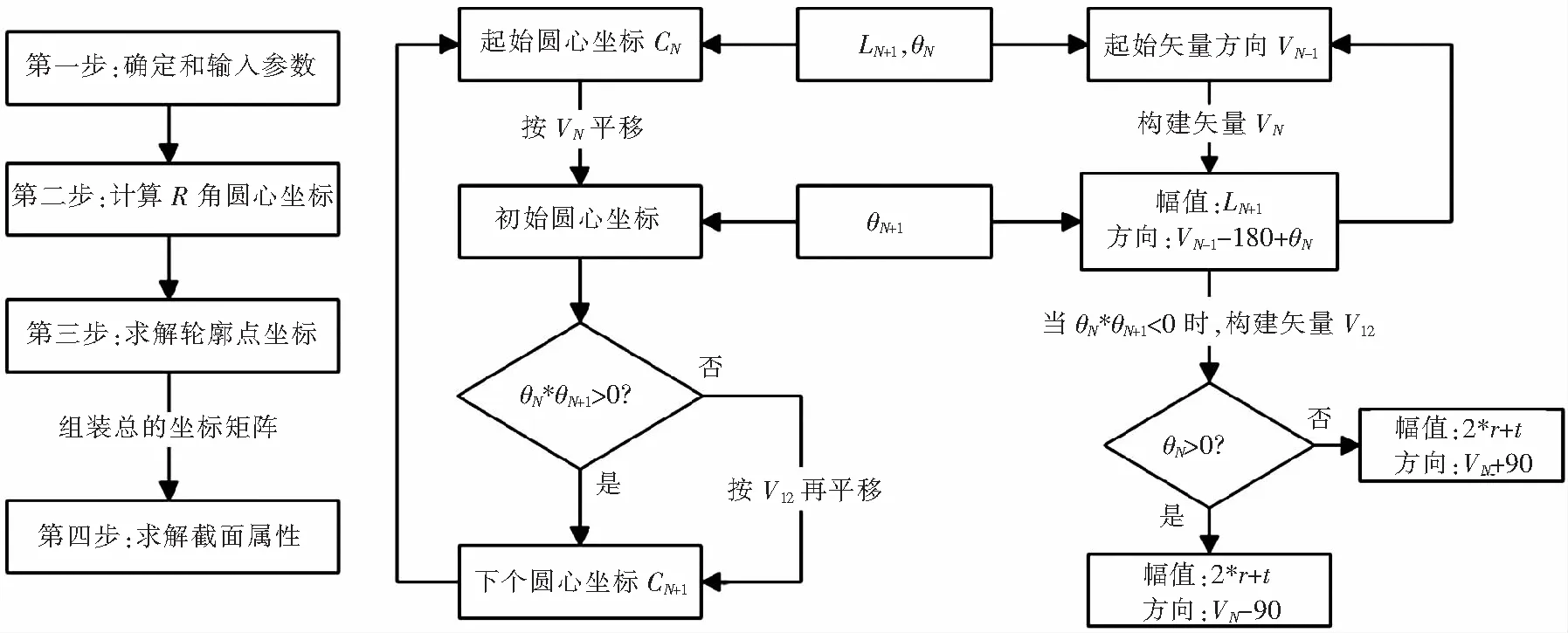
图4 分析流程图
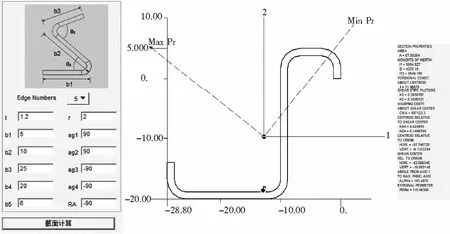
图5 软件界面
3 算例验证
针对直升机结构常用的典型钣金角材,分别采用常规截面定义方法和本文考虑倒角的高精度定义方法进行计算和验证。选取L型材、两种不同截面和不同倒角的Z型材为算例,截面几何参数如表1所示。

表1 典型型材几何参数
分别对上述三种典型型材进行高精度定义,得到本文方法与常规简化方法的截面形状。以Z2r2型材为例,形状对比如图6所示。
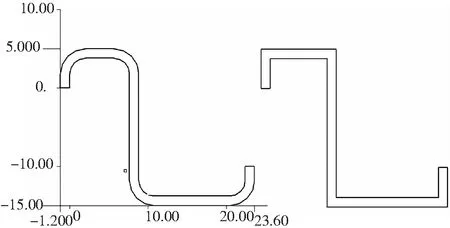
图6 截面形状对比
常规方法计算的截面参数与本文精确计算结果的误差对比如表2所示。
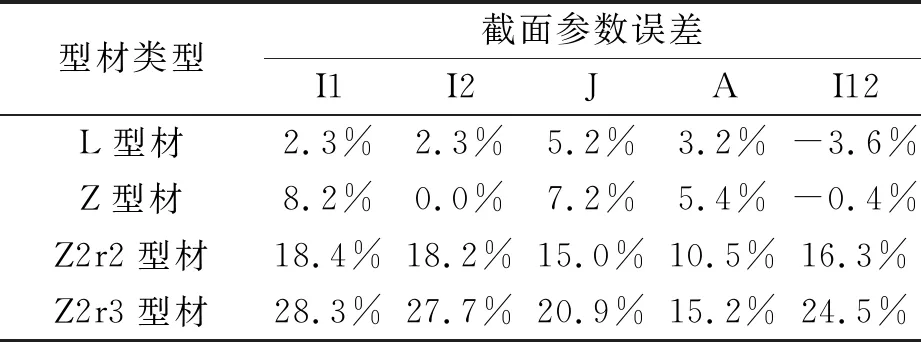
表2 截面参数计算结果对比
从表2中结果可知,采用常规简化截面定义方法与本文方法定义的截面参数差异明显。当倒角为2°时,误差与倒角的个数成正比,不同截面的惯性矩的最大误差达到了18.4%,面积最大误差达到了10.5%。对比不同倒角的计算结果,当采用3°倒角时,Z2型材的截面惯性矩和面积误差分别增加到28.3%和15.2%。
4 结论
本文从钣金型材的截面几何特征出发,对带倒角的复杂形状钣金型材截面的参数化方法进行了推导,并基于MSC.Patran软件平台,开发了相应的截面定义模块,可用于直升机真实钣金结构的动力学快速建模。基于该模块,通过三种典型钣金截面的对比表明,对比常规方法,本文计算结果有效提高了带倒角截面的惯性矩和截面积计算精度,特别是对于倒角个数和倒角角度较大的复杂截面,大幅提高了结构动力学的仿真分析精度。
由于本方法是基于钣金型材等厚度和倒角不变的假设,难以适用于直升机上其他的截面型材,如机加型材或复合材料型材等,其他型材的参数化方法仍待进一步研究。
