基于传递系数及工艺能力指数的公差分配方法

梁云瑞，龚仔华，陈玉娟

(1.海装武汉局驻南昌地区军事代表室，江西 南昌 330024；2.航空工业洪都，江西 南昌 330024)

0 引言

航空装备对产品快速装配及模块化换装需求越来越高。相应地，零部件结构设计时对互换性需求逾加强烈。产品公差设计已成为零部件设计中的一项重要技术。目前行业上常用的公差分配方法有经验法、等公差数值法、等公差精度法等。这些公差分配方法由于没有充分考虑组成环传递系数的差异性以及生产车间的实际工艺能力而具有一定的局限性。

本文提出了一种基于传递系数、工艺能力指数的公差分配方法。该方法以组成环公差满足最小工艺能力指数为约束条件，按照等影响量法进行公差分配，并基于工艺能力指数及传递系数对组成环公差进行优化。公差分配主要包含组成环公差初始分配与公差补偿优化两大部分。

1 公差分配方法

1.1 工艺能力指数

在已知零件具体材料、结构形式及尺寸、加工工艺等条件下，车间加工某尺寸可能产生误差的大小称为该尺寸加工方法的“工艺能力”[1]。按照经典的“3σ原则”，取ω=[-3σ，3σ]代表着按照具体加工条件的工艺能力。当ω较小时，加工方法的误差范围小，工艺精度高；反之ω较大时，代表工艺精度低。

为了表征设计尺寸公差与工艺能力的关系，引入工艺能力指数Cp为设计尺寸公差与工艺误差比值[1]，即：

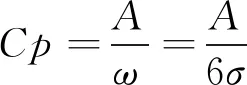
(1)

式中σ为加工零件尺寸的标准差，工艺能力指数Cp代表尺寸公差的工艺性。考虑产品制造水平及经济性，在公差设计时Cp取1.15至1.2。

1.2 等影响量公差分配法

等影响量公差分配法的原则是：调整设计尺寸公差使装配尺寸链中各组成环公差对封闭环产生相同的影响量[2]。组成环传递系数越高，则应赋予该组成环越小的设计公差值。

对由n个相互独立的尺寸Xi(公差Ai)及已知封闭环X0(公差A0)组成的尺寸链，当采用极值法时，其组成环公差分配按如下公式推导：

(2)

在封闭环公差A0确定的情况下，组成环公差Ai计算如公式(3)：

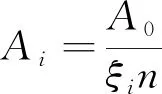
(3)

当采用概率法时，其公差分配按如下公式推导：

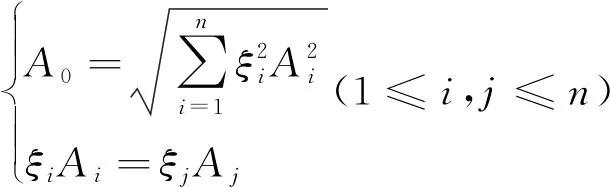
(4)

按照公式(4)，在封闭环公差A0确定的情况下，组成环公差Ai计算如公式(5)：

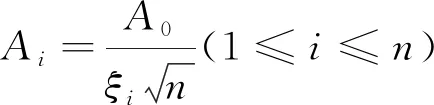
(5)

1.3 公差补偿优化方法

按照等影响量公差分配进行公差分配后，当部分组成环不满足最小工艺能力指数(令为Cpmin，预设值)的约束条件，需对组成环尺寸公差补偿优化。为提高优化效率，应首先提高工艺能力指数裕度及传递系数高的组成环尺寸精度。工艺能力指数裕度(ΔCp=Cp-Cpmin)，补偿系数是指公差优化时，工艺能力指数裕度为正的组成环可用于补偿工艺能力指数为负的组成环的能力。补偿系数由组成环的工艺能力指数裕度与传递系数ξ共同决定。补偿系数随工艺能力指数裕度与传递系数的增加而增加，呈正比例关系。令补偿系数M，M可由公式(6)计算:

M=ΔCp×ξ=(Cp-Cpmin)×ξ

(6)

公差补偿优化时，将所有负工艺能力指数裕度的组成环公差增加至零工艺能力指数裕度，按照极值法或概率法计算组成环公差调整后的对封闭环的影响总量。另一方面，将所有正工艺能力指数裕度的组成环公差按照补偿系数等比例降低，按照极值法或概率法计算组成环公差调整后的对封闭环的影响总量。令组成环公差增加与组成环公差降低对封闭环的影响总量相等，计算所有组成环调整后公差值及工艺能力指数，并再次评价、补偿，直至所有组成环均满足最小工艺能力指数要求。

2 公差分配流程与算法

对由n个相互独立的尺寸Xi及已知封闭环X0组成的尺寸链，将已知封闭环X0公差为A0，以最小工艺能力指数Cpmin为约束条件，基于等影响量公差原则的公差分配算法如下：

1)根据部件装配关系绘制尺寸链关系图，并列出尺寸链函数。

X0=F(X1，X2，…，Xn)(1≤i≤n)

(7)

2)提取组成环Xi并按式(8)计算其传递系数ξi。

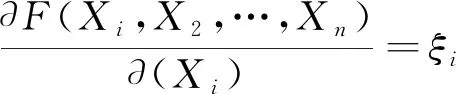
(8)

则：

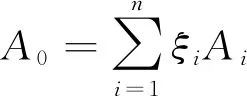
(9)

3)根据零件特点通过车间获取组成环Xi的工艺能力ωi，根据应用场合选择极值法或概率法作为公差计算方法。

4)按照Ai=ωi×Cpmin计算组成环最小工艺能力指数公差，验算所有组成环公差累计值是否满足封闭环公差A0要求，如不满足要求则人为降低Cpmin或提高A0值。

5)按照公式(3)或公式(5)进行等影响量公差分配，求得组成环Xi公差Ai。

6)对任意Ai，按照式(10)与式(11)计算其工艺能力指数Cpi与工艺能力指数裕度ΔCpi。

Cpi=Ai/ωi

(10)

ΔCpi=Cpi-Cpmin

(11)

7)判断组成环Xi公差Ai的工艺能力指数裕度ΔCpi正负，将其负值(及0值)、正值分别分为子数量为n-的An-组及子数量为n+的An+组，则n-+n+=n。

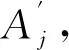
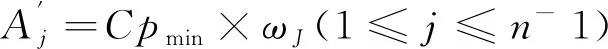
(12)

9)对An-组，计算An-组中组成环公差值调整后对封闭环的影响总量S-。

采用极值法时按公式(13)计算：

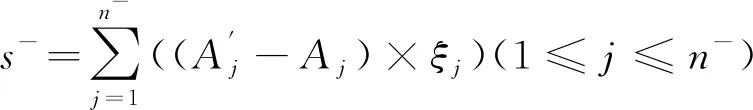
(13)

采用概率法时按公式(14)计算：

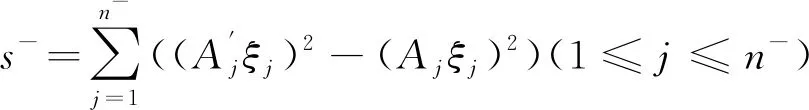
(14)

10)对An+组，逐一计算An+组组成环补偿系数Mk。

Mk=ξk×ΔCpk(1≤k≤n+)

(15)

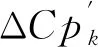
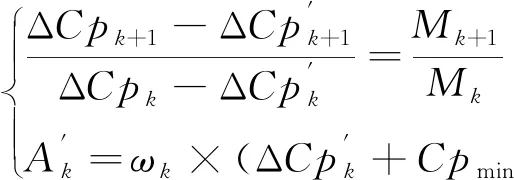
(16)

12)对An+组，计算An+组组成环公差值调整后对封闭环的影响量S+。

采用极值法时按公式(17)计算：

(17)

采用概率法时按公式(18)计算：

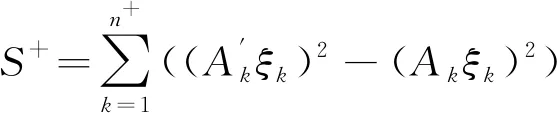
(18)

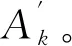
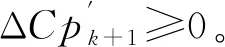
15)最终求取所有组成环Xi公差Ai。

公差分配算法流程如图1所示。在按等影响量进行公差分配前，已经对组成环的最小工艺能力指数进行了验算。按等影响量进行公差分配后，若出现部分组成环公差不满足最小工艺能力指数要求，在补偿优化过程中随着迭代次数增加，不满足要求的组成环数量越来越少，补偿优化算法是收敛的。

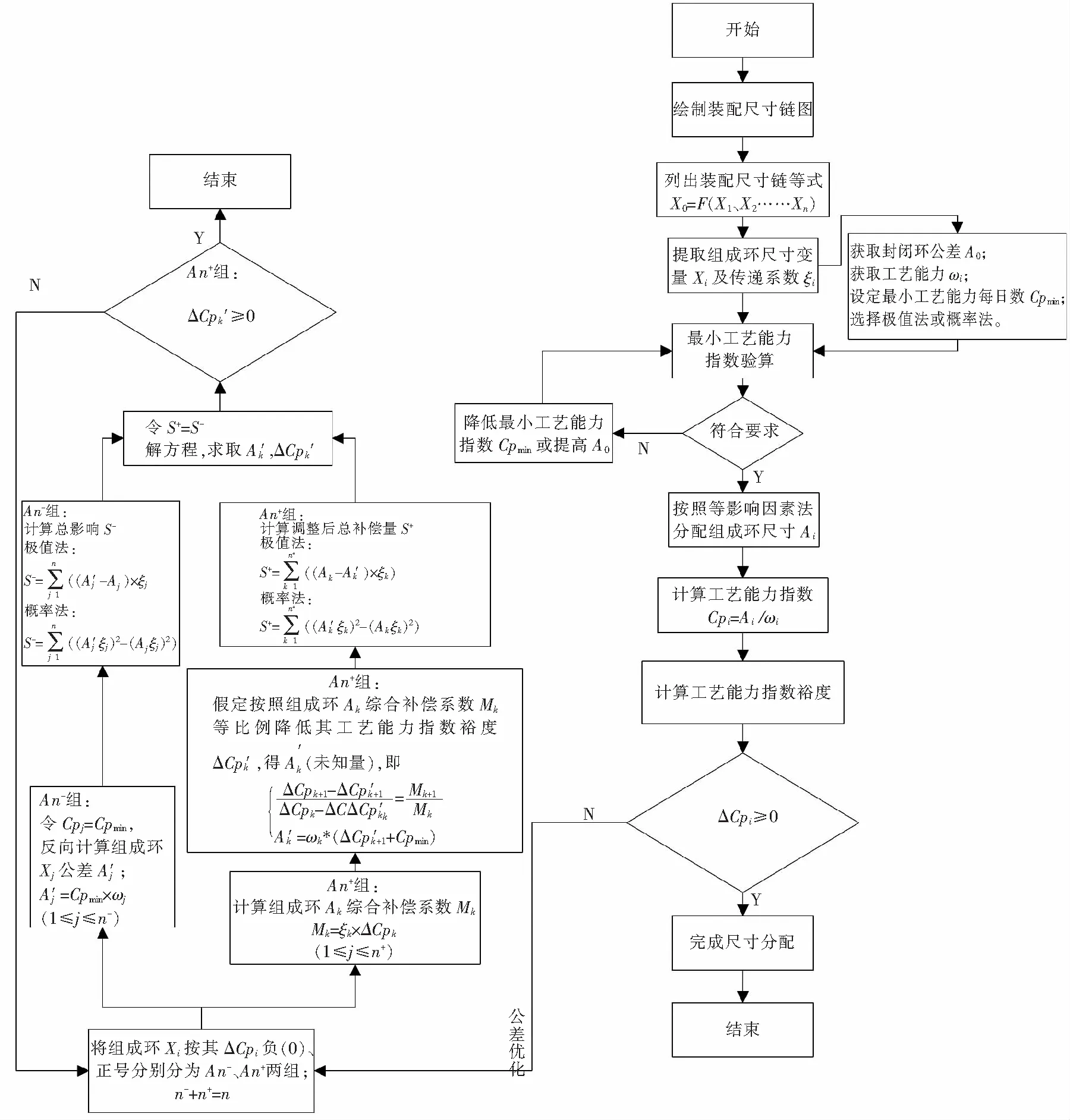
图1 公差分配算法流程

与传统的公差分配方法相比，本文提出的基于传递系数及工艺能力指数的尺寸链公差分配方法具有以下优点：

1)公差分配具有明显的方向性

引入传递系数，按照等影响量法进行公差分配。通过传递系数的计算，可直接找到对封闭环具有关键影响的组成环，从而对其严格控制；反之，对传递系数低的组成环则可放宽公差要求。

2)工艺性评价更合理

相比考虑了工艺能力的等精度公差分配方法，本文算法采用工艺能力指数的评价方法，充分考虑零件材料、结构形式、加工工艺及车间制造水平等因素，因此更为合理。

3)算法可实现性强

本文提出的公差分配算法具有收敛性，尽管在公差补偿优化阶段需要多次迭代，但是该算法可借助计算机辅助技术提高计算效率与精度。

3 公差分配方法应用

以下采用本文提出的公差分配方法对相邻舱段上前、后滑块上表面装配平面度的公差进行分配，以验证方法的有效性。

装配形式如图2所示：舱段1(钛合金)壁厚5 mm、舱段2(钢)壁厚为10 mm，利用舱体中心线位置处的两件阶梯定位销定位，进行盘式连接。两件滑块(前向宽度为40，侧向宽度为130)分别安装在舱1、舱2上表面，装配后要求两件滑块上表面平面度不低于0.3 mm。零件基本尺寸如图2所示，其中定位销配合尺寸按设计手册确定为φ11H8/f7。

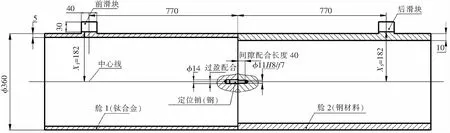
图2 部件装配关系示意图

对装配图进行分析发现，前、后滑块平面度装配偏差主要由以下几个方面组成：

1)舱1、舱2安装滑块的上表面距舱体水平基准面的高度偏差；

2)滑块与舱体配合的下底面距上表面高度偏差及平行度偏差；

3) 定位销与定位销孔(φ11H8/f7)间隙造成的轴线错位偏差；

1)-3)偏差累计记为H。

4)舱1、舱2在前向方向的弯折角度α1，α2偏差。

5) 舱1、舱2对接后，因φ11H8/f7定位销孔配合间隙造成舱2扭转角度β。

根据上述分析，前、后滑块安装后的空间偏差关系如图3所示。为计算2个空间平面的平面度，以前滑块左后角为坐标原点，X0Y面与对接端面平行，逆前向为X轴，平行于舱1的两个定位销孔连线方向为Y轴，高度方向为Z轴建立坐标系。为便于计算，α1、α2均以+X方向为0度，逆时针为正；β以+Y方向为0度，逆时针为正。因α1、α2、β角度很小，其正弦值可直接近似按角度弧度值计算。最终，前、后滑块其余7个角点坐标如图3。

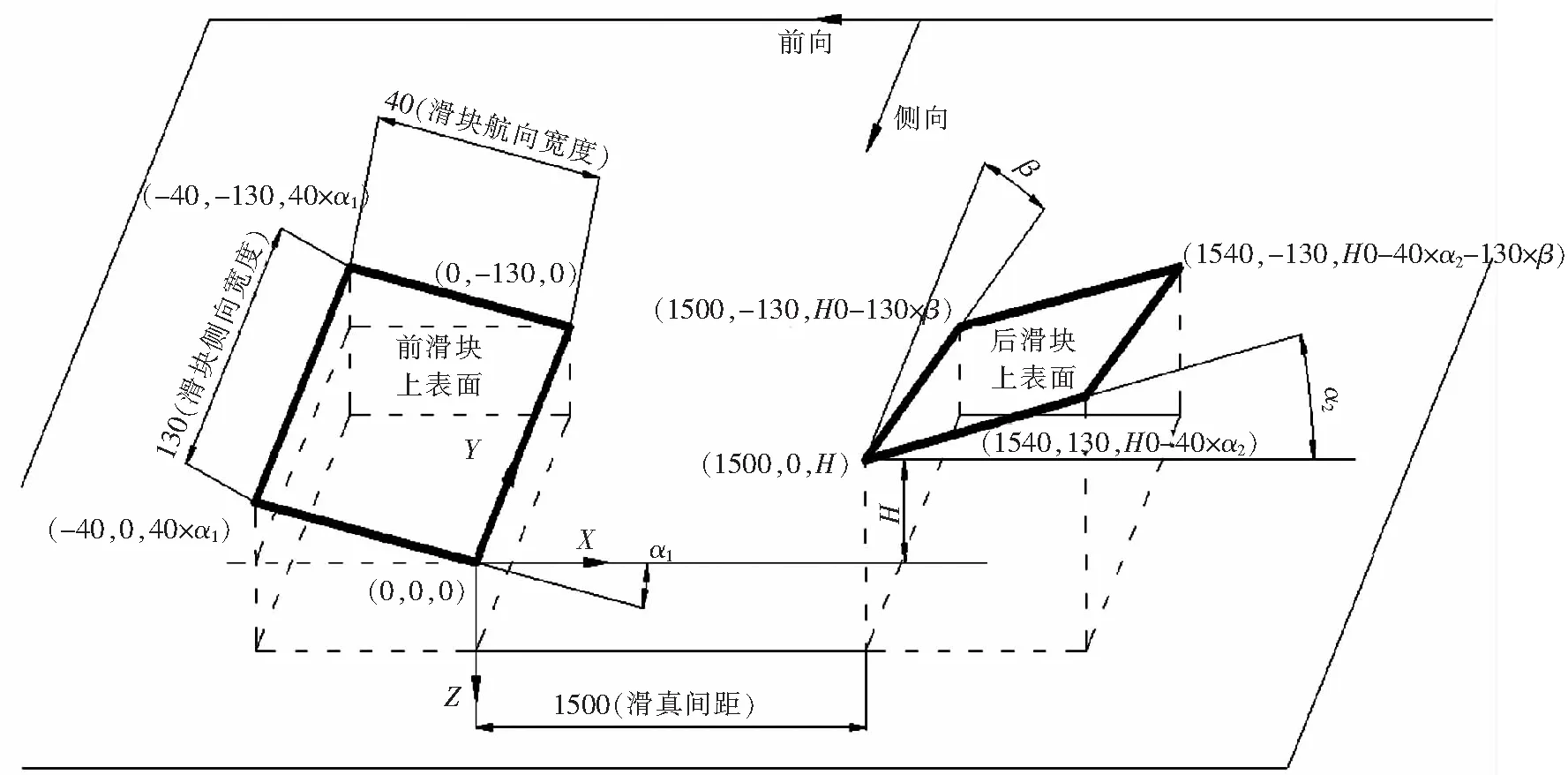
图3 前、后滑块装后空间示意图

平面度公差带没有特定基准方向，其评定应按照最小条件原则。前、后滑块前向宽度与侧向宽度相等。经计算，当平面度公差带平面与X0Z面呈(α1+α2)/2夹角，并与Y0Z面呈β/2夹角时，公差带值最小。根据点到平面距离公式，平面度公差值可按式(19)计算。

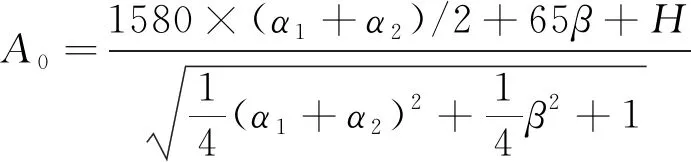
(19)

影响前、后滑块装配平面度的零件尺寸如表1。因舱体装配后弯折角α1、α2具有方向性，表中舱1、舱2端面垂直度公差A2、A5的正、负方向分别与α1、α2相对应。当舱1、舱2端面垂直度公差为0.5A2、0.5A5时，计算时公差带取值范围为(-0.5A2，0.5A2)、(-0.5A5、0.5A5)，即其公差带宽分别为垂直度数值的2倍。

表1 影响装配平面度的零件尺寸列表

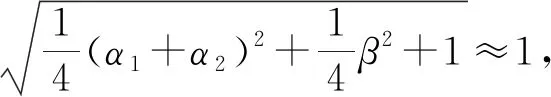
A0=A1+2.08A2+A3-A4+2.08A5-A6+A7+

A8-A9-A10+1.17X11-1.17X12

(20)

根据各零件在车间加工工艺，获取其零件尺寸工艺能力数据。按照本文提供的公差分配方法，取最小工艺能力指数为1.2，采用概率法对前、后滑块平面度按照等影响初次分配及优化后的公差分配值如表2。如表所示，采用本文提出的方法时，按照等影响量法进行初始分配后，传递系数高的组成环垂直度仅0.042，公差过严。传递系数低的组成环平行度可达0.17。作为位置公差，其数值与尺寸公差相同，显然是不合理的。但经过补偿优化，工艺能力指数高的组成环公差值迅速下降，经迭代使所有组成环公差均满足最小工艺能力指数1.2的要求，达到公差分配目标。通过上述应用实例，验证了该公差分配方法的有效性。

表2 采用本文方法完成的公差分配结果

4 结论

本文以实现尺寸链公差合理分配为目标，提出了以组成环公差满足最小工艺能力指数为约束条件，按照等影响量进行公差分配，并基于工艺能力指数及传递系数对组成环公差进行补偿优化。依据上述原理，推导了公差分配与补偿优化计算公式，并给出了算法流程。利用本文提出的公差分配方法，完成了双定位销盘式连接的相邻舱段上前、后滑块装配平面度的公差分配，验证了该方法的有效性。