倾转旋翼弹性等速万向铰桨毂运动仿真

周 文，林 展，覃海鹰，冯萌萌

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

高速化是未来直升机发展的一个大趋势。倾转旋翼作为一种先进的旋翼构型，与共轴旋翼一起组成了高速直升机旋翼构型的两大发展方向。国外，军机方面，美国波音公司的V-22已实现批产交付，V-280已完成科研试飞；民机方面，AW609已处于取证阶段，预计2022年即可交付客户使用。国内的倾转旋翼机的研制工作还处于起步阶段。美国V-22的研制经验表明，万向铰桨毂是三支臂倾转旋翼机必不可少的关键部件。十字万向铰是机械领域最常见的一种万向铰构型(见图1)。但该构型存在转速周期波动的固有缺陷，应用于直升机时会导致全机产生较大的振动载荷，由此诱发系列的旋翼/全机动力学问题。

图1 金属十字万向铰构型

1 等速万向铰构型选择

金属十字万向铰构型的转速波动关系[1]可表示为：

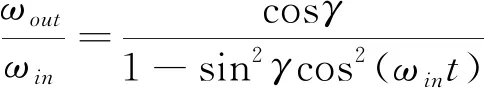
(1)

其中，ωin、ωout分别表示输入轴、输出轴角速度，t表示时间，γ表示倾转角。当γ=12°时，转速波动如图2所示。

由图2可知，转速比波动幅度达2.3%。为实现等速传动，工程上采用双十字轴式万向节[1]设计传动，即两个万向节夹角一致，且第一个万向节的从动叉与第二个万向节的主动叉在同一平面。这种构型允许有较大的轴间夹角，轴承密封性好、效率高、制造工艺简单、工作可靠，广泛应用于越野汽车转向装置设计。但由于双十字万向节之间存在传动轴设计，不满足直升机桨毂尺寸紧凑的要求，该解决方案不适于倾转旋翼机桨毂设计。

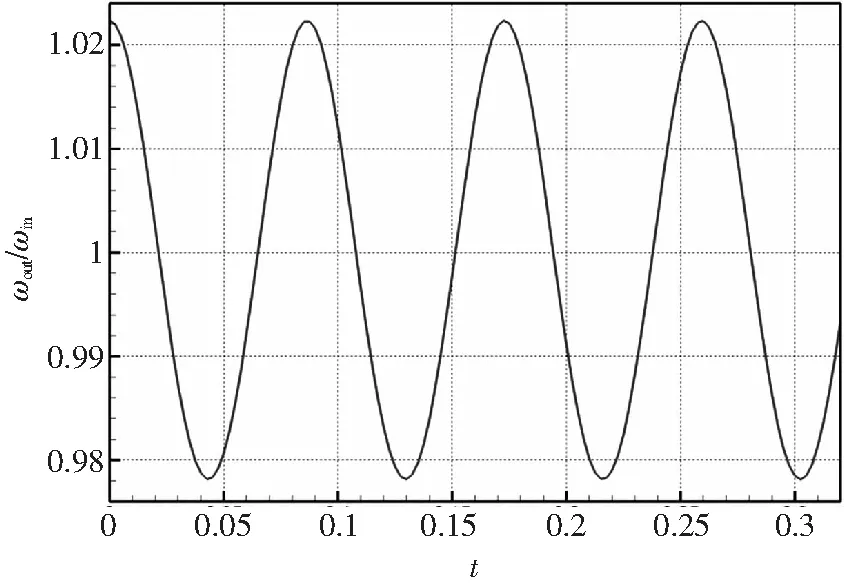
图2 输入轴与输出轴成12°时的转速波动示意

目前，国外比较成功的等速万向铰构型(见图3)主要包括两类：①基于弹性轴承的等速万向节，例如AW609[2]、XV-15[3]、V-22[4]及 ERICA桨毂构型[5]；②基于金属结构的等速万向节，例如 Sikorsky研制的变直径倾转旋翼桨毂[6](中央使用球铰定心，外加3个连杆传递扭矩)及韩国研制的无人倾转旋翼机桨毂[7](使用球柔式等速万向节)。

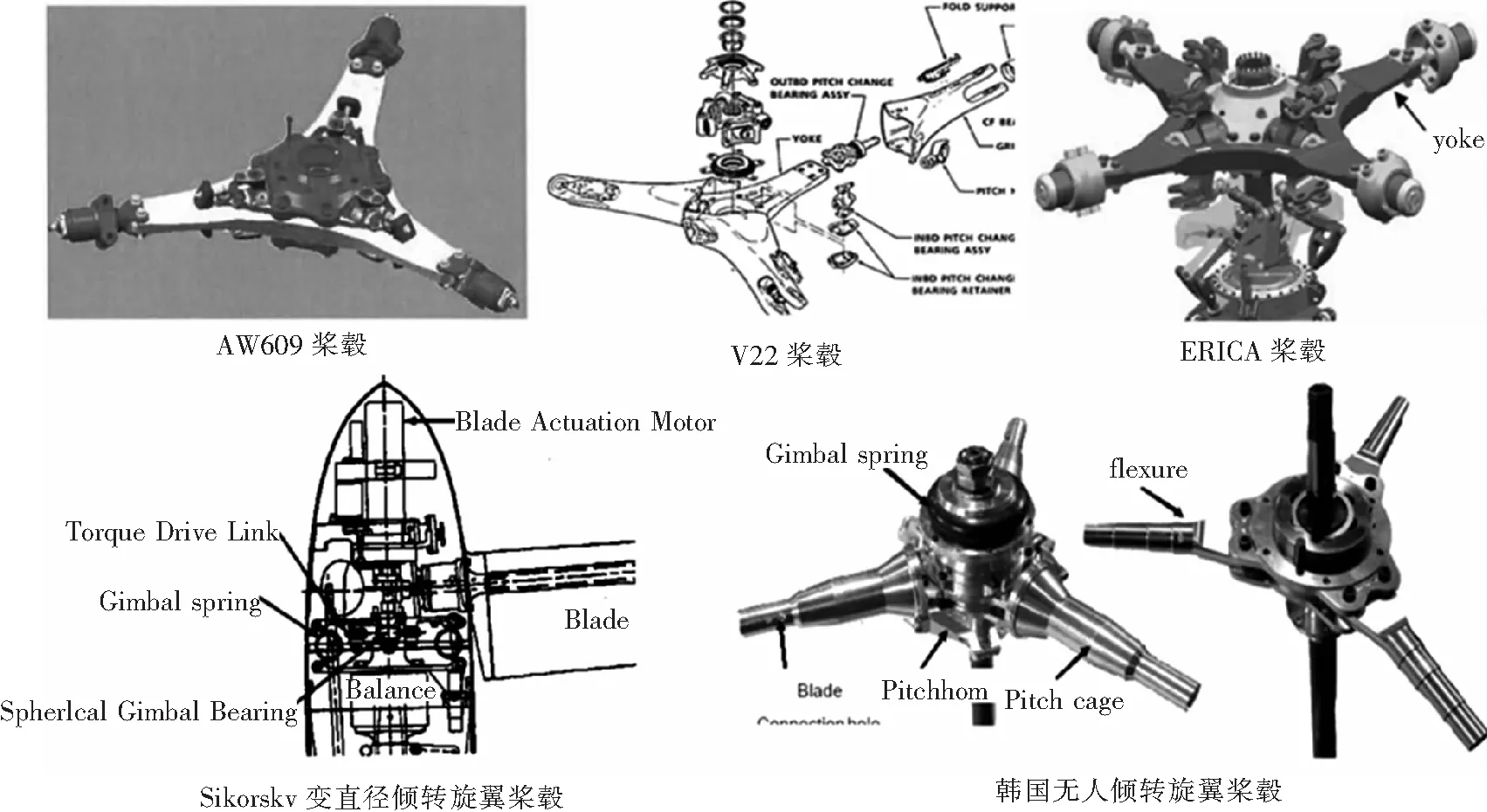
图3 国外几种等速万向铰构型示意

对比分析认为，V-22型机采用的等速万向铰构型(Lord公司研制)已经得到了成熟应用，很好地满足了可靠性和维护性要求。本文仅针对弹性等速万向铰开展设计及验证工作。

2 弹性等速万向铰构型分析

弹性等速万向铰主要结构如图4所示。万向铰功能结构件主要由弹性万向铰轴承、中心件、连接件和三组弹性连杆构成。其中，中心件与旋翼主轴相连，负责主轴扭矩的传递；万向铰轴承实现挥舞运动及挥舞切力的传递；三组弹性连杆的两个端头均为弹性关节轴承，与中心件连接，以此来实现主轴扭矩的传递和运动协调。此外，这种构型设计使得旋翼旋转时，交变扭矩在桨毂处自平衡(如图5所示)，即没有交变扭矩传递到旋翼轴上，不会引起不利振动。

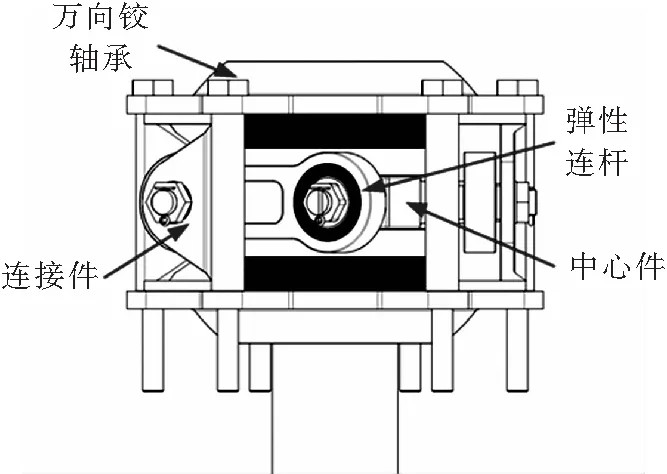
图4 弹性万向铰构型

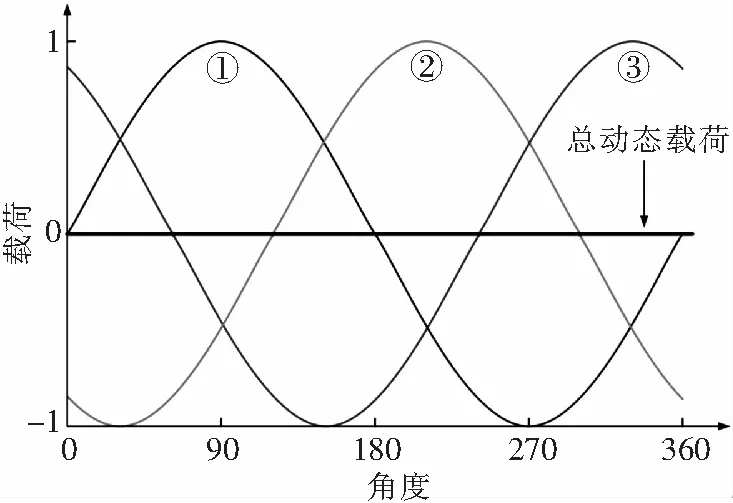
图5 弹性万向铰交变力矩

3 弹性等速万向铰等速原理

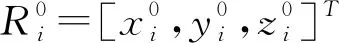
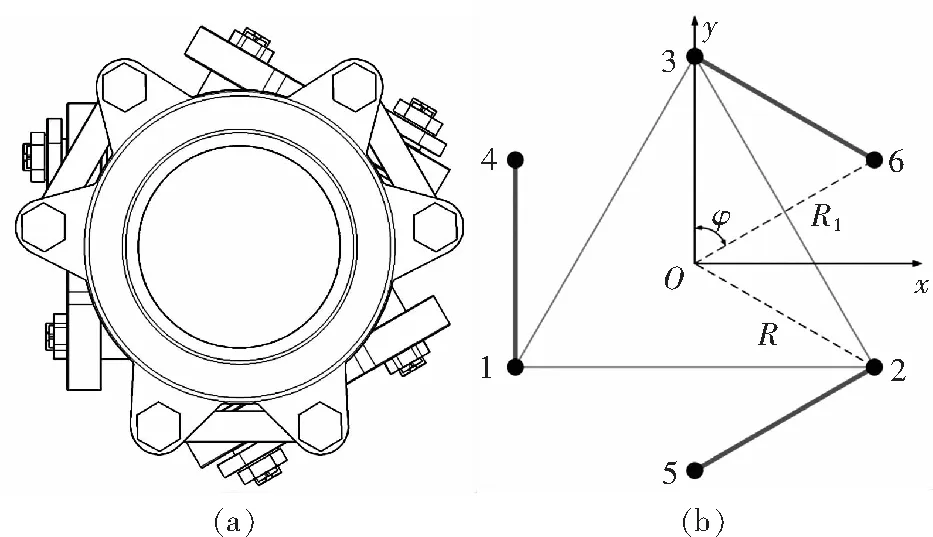
图6 弹性万向铰实物模型(a)及简化示意(b)

这里，上标“0”表示初始时刻，上标“T”表示转置。

将桨毂盘面倾转γ角度(简单起见，绕y轴旋转)，在三组弹性连杆的作用下，标号4，5，6三个点构成的平面(记为∑2)仍然过坐标原点O。建立如图7所示的坐标系O-x′y′z′。

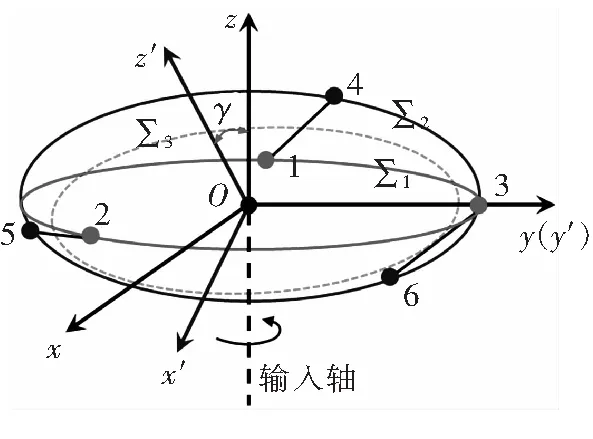
图7 桨毂盘面倾转角度后的坐标系示意

其中，z′轴垂直于∑2。与中心件固连的轴承中心(标号1, 2, 3)构成的平面记为∑1。坐标系O-xyz与O-x′y′z′之间的对应关系为：

(2)

设t时刻，旋翼主轴、桨毂盘面分别旋转θ1(t)、θ2(t)角度。此时，与中心件固连的三个轴承中心(标号i=1, 2, 3)在O-xyz坐标系下的坐标为：

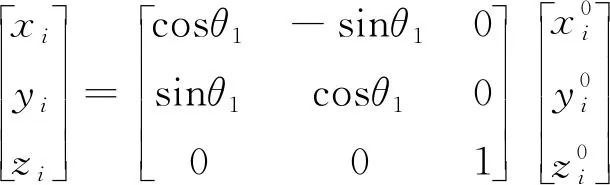
(3)

相应地，与中央件固连的三个轴承中心(标号i=4, 5, 6)在O-x′y′z′坐标系下的坐标为：

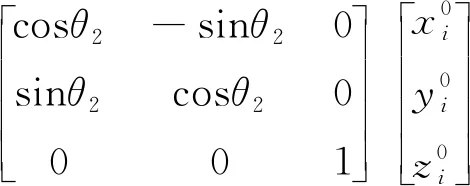
(4)

这里，上标“0”代表初始时刻。

根据O-xyz与O-x′y′z′之间的对应关系可知，与中央件固连的三个轴承中心(标号i=4, 5, 6)在O-xyz坐标系下的坐标为：

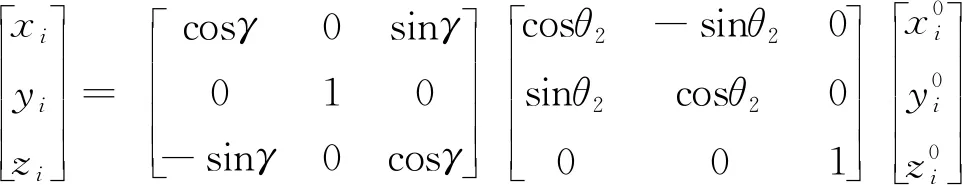
(5)

显然，在旋转过程中，三组弹性连杆的中心的运动轨迹相同，且构成的旋转面(记为∑3，如图7绿色虚线所示)始终过原点O。在O-xyz坐标系下，设∑3的平面方程为：

Ax+By+Cz=0

(6)

事实上，在桨毂盘面倾转的瞬间，轴承组3-6及2-5的中心均在平面∑3上，即有：

令R1=βR，化简式(7a)、式(7b)，得：

Aβsinφcosγ+B(1+cosφ)-Cβsinφsinγ=0

(8a)

根据上述两式，解得：

A=β(β+cosφ)sinγ

(9a)

B=βsinφsinγ

(9b)

C=β2cosγ+βcosφ(1+cosγ)+1

(9c)

由于旋转过程中，轴承组3-6的中心始终位于平面∑3上，故有：

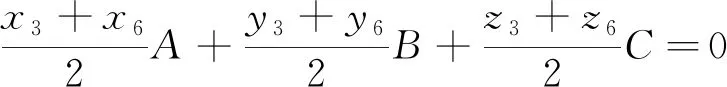
(10)

其中，

化简式(10)，得：

sin(φ-θ1)-sin(φ-θ2)(1+βcosφ)-

βsinθ1+βsinφcos(φ-θ2)=0

(12)

进一步整理，得：

β(sinθ2-sinθ1)+sin(φ-θ1)-sin(φ-θ2)=0

(13)

根据三角函数和差化积公式，式(13)可化为：

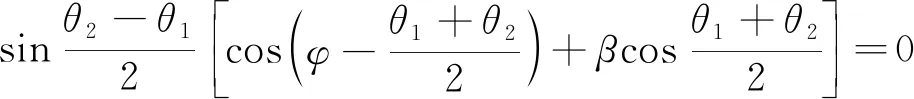
(14)

显然，当t连续变化时，要使式(14)恒成立，只有

θ2(t)-θ1(t)=2kπ,k∈Z

(15)

结合初值条件θ2(0)-θ1(0)=0，知式(15)中k=0，即：

θ1(t)=θ2(t)

(16)

因此，旋翼主轴与桨毂盘面转速相等，证实该弹性万向铰构型满足等速设计预期。

4 弹性等速万向铰运动仿真

首先，进行弹性连杆两端关节轴承的径向长度计算。

不失一般性，以轴承组3-6的径向长度计算为例。根据式(11)，易得：

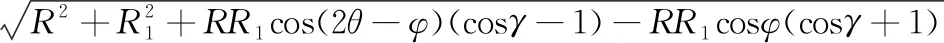
(17)

其中，θ表示任意时刻的旋转角度(根据等速原理，知θ1=θ2=θ)。其它两组弹性连杆的长度可类似得到，这里不再赘述。

图8给出了R=200 mm，γ=10°时，三组弹性连杆的径向长度随时间的演化曲线。由图可以看出，d3,6和d2,5的初始值均为200 mm，而d1,4的初始值却大于200 mm；三组弹性连杆的径向长度均呈周期变化，且单个弹性连杆的实际伸缩位移幅值约为3 mm。这是三支臂倾转旋翼弹性万向铰桨毂的连杆只能选用弹性连杆(而非金属连杆)的一个最直接的原因：在旋转过程中，连杆组件需要弹性轴承实时补偿位移。

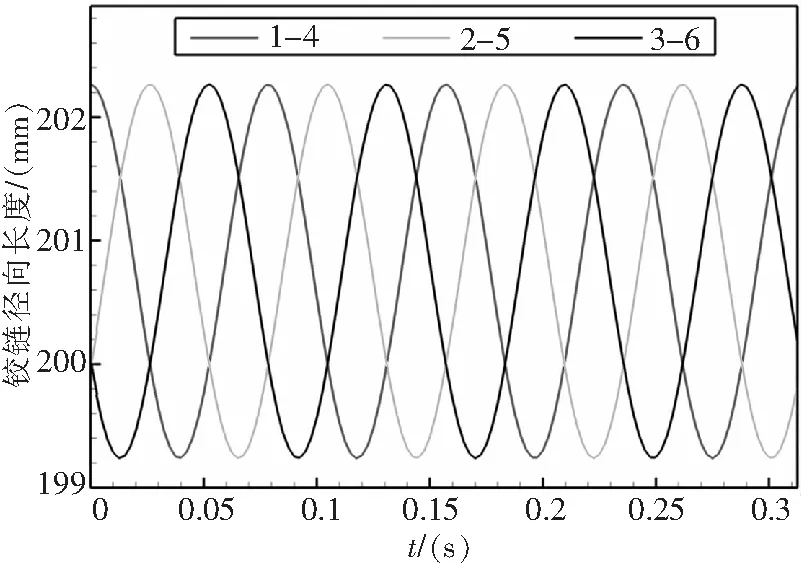
图8 三组弹性连杆的径向长度随时间的演化

其次，验证旋转主轴与桨毂盘面的转速波动为零。具体方法为：

1)根据经验估计出弹性连杆所需的径向刚度Kr，这里取Kr=40 kN/mm；

2)根据式(20)，计算弹性连杆的实际伸缩位移Δdi,i+3，进而得出弹性连杆径向载荷Fi,i+3(Kr,Δdi,i+3)；

3)计算输入、输出轴的合力矩∑Min、∑Mout，验证二者是否为零。

简单起见，这里暂不考虑弹性连杆扭转、弯曲及任何气动外力的影响，倾转角γ=10°。图9给出了输入、输出轴总力矩的模随时间的变化过程，可以发现输入、输出轴的总力矩为零，从而验证了输入、输出轴转速相等。图10给出了三组弹性连杆固支端、活动端及中心点的运动轨迹。从图10可以看出，三个点的旋转轨迹共圆心。图11给出了不同倾转角度下，弹性连杆3-6的相对径向位移随时间的演化。图11显示：弹性连杆的实际伸缩位移幅值随着倾转角的增大而增大，且增长趋势呈非线性变化。

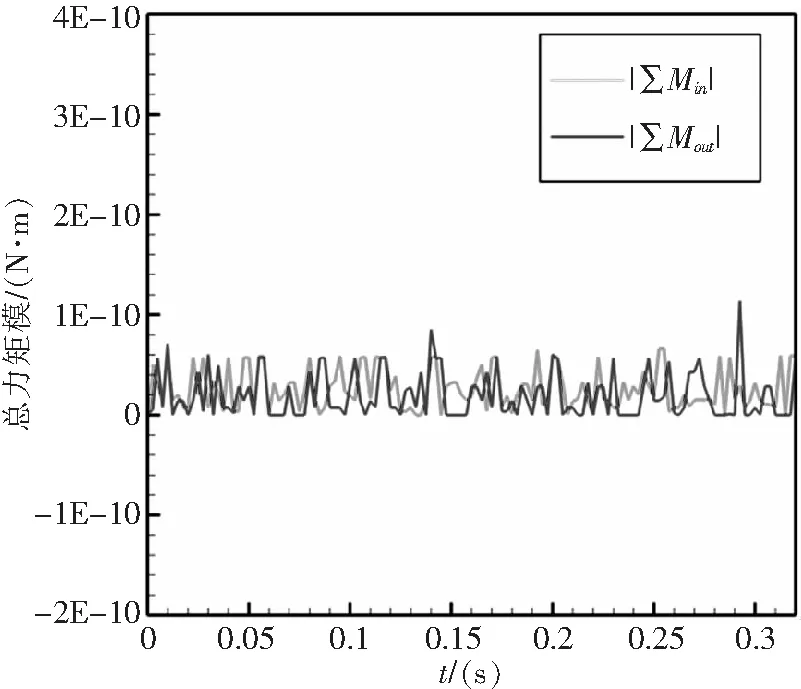
图9 输入、输出轴总力矩的模随时间的演化

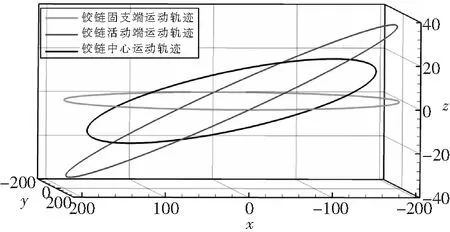
图10 弹性连杆固支端、活动端及中点的运动轨迹(单位: mm)

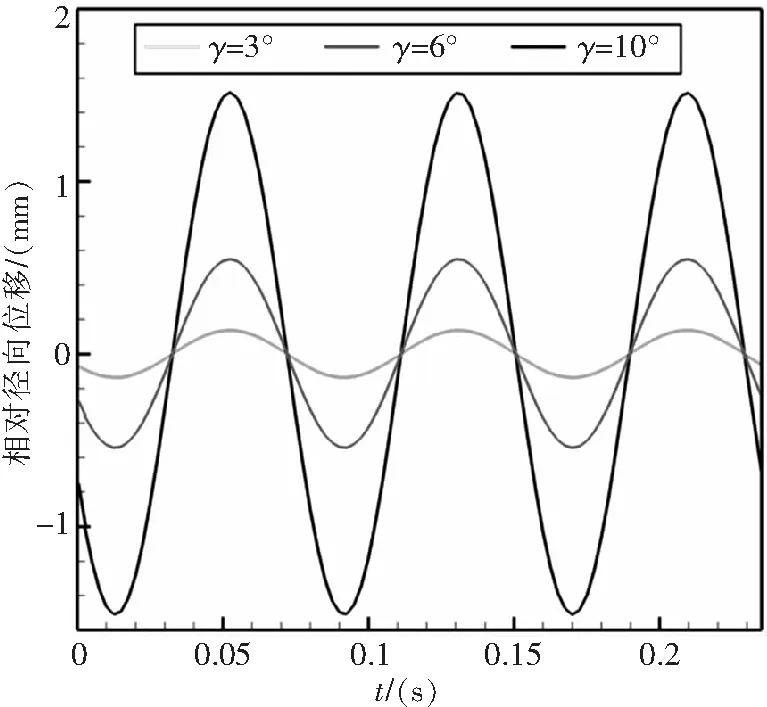
图11 γ不同时，弹性连杆3-6的伸缩位移随时间的演化

最后，考虑空气阻力对弹性连杆伸缩位移的影响。这里忽略弹性连杆的弯曲，倾转角γ=10°，Kr=40 kN/mm，空气阻力方向与桨毂盘面旋转速度方向相反，大小设为1000 N。图12给出了空气阻力对弹性连杆3-6的径向长度的影响。从图12可以看出，考虑空气阻力后，弹性连杆的径向长度整体变大，但各时刻的增加量并不相同。这是因为弹性连杆在克服空气阻力时，径向载荷增大，从而径向长度变大。另一方面，在旋转过程中，弹性连杆方位角不断变化，空气阻力在径向的分量也随之发生变化，因此弹性连杆径向长度在各时刻的增加量并不相同。

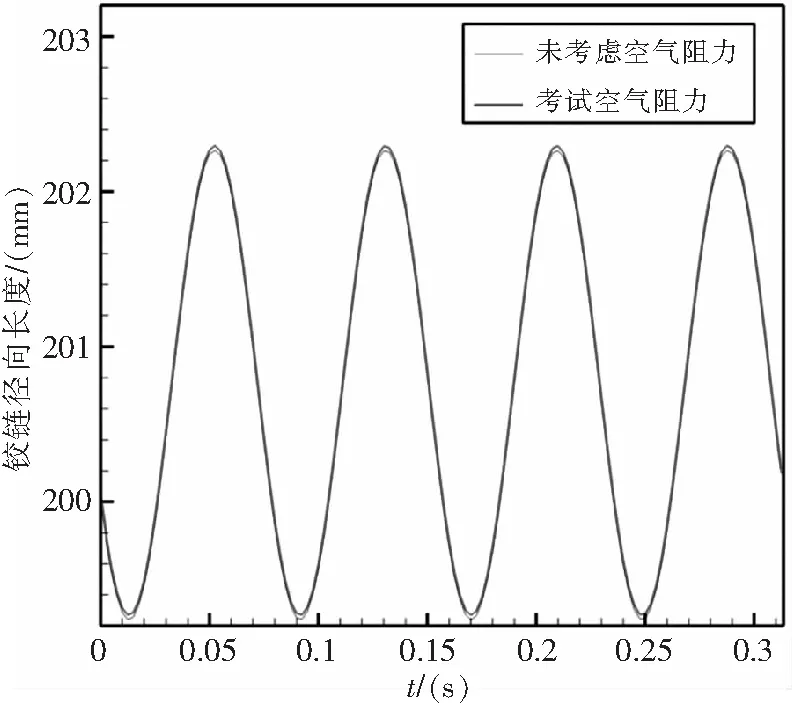
图12 弹性连杆3-6的径向长度随时间的演化

5 结论

本文首先给出了一种弹性等速万向铰构型，然后详细证明了其等速原理，最后基于等速原理建立运动仿真模型，进行了运动仿真分析。得到了弹性连杆径向长度和输入、输出轴总力矩模在旋转过程中随时间的演化规律，以及桨毂盘面倾转角度、空气阻力对弹性连杆径向位移幅值的影响情况。仿真结果一方面从理论上验证了弹性万向铰的转速波动为零，另一方面可结合外部载荷输入，为弹性连杆的径向刚度指标设计提供理论依据。此外，本文为复杂气动载荷状态下弹性等速万向铰的运动仿真、零部件之间的运动干涉检验以及相关指标设计的进一步优化奠定了基础。